基于 MEEMD 算法的二冲程柴油发动机机体振动分析

贺献忠 徐麟绍 高超

摘要：二沖程低速柴油机具有复杂的振动特性，传统的经验模态分解（EMD）算法对其振动信号处理效果不理想。为此，采用修正集合经验模态分解（MEEMD）算法对低速柴油机机体振动信号进行分解。首先，采用三轴加速度计测量发动机机体振动。然后利用均方根（RMS）对三轴振动强度进行分析。最后，对x轴上的信号进行MEEMD分析。结果表明：砌块在x轴方向的振动强度最大;与EMD算法相比，MEEMD算法可以抑制模态混合，有助于更好地识别块振动激励。

关键词： 低速柴油机 振动 信号处理 修正集合经验模态分解

中图分类号：TM935

Analysis of the Block Vibration of Two-Stroke Diesel Engines Based on

the MEEMD Algorithm

HE Xianzhong1*  XU Linshao2  GAO Chao3

1. Merchant Marine College， Shanghai Maritime University， Shanghai， 201306 China;2. Zhejiang Shipping Group Zhehai Shipping Co.， Ltd.， Hangzhou， Zhejiang Province， 311500 China;3. Transportation Department，  Shougang Mining Corporation， Tangshan， Hebei Province， 064404 China

Abstract：The two-stroke low-speed diesel engine has complex vibration characteristics， and the conventional empirical mode decomposition （EMD） algorithm has the unsatisfactory processing effect of its vibration signals， so the modified ensemble empirical mode decomposition （MEEMD） algorithm is adopted to decompose the signals of  the block vibration of the low-speed diesel engine. First， a triaxial accelerometer is used to measure the block vibration of the engine. Then， the root mean square （RMS） is used to analyze the vibration intensity of three axes. Finally， the MEEMD algorithm is used to analyze the signals on the x-axis. The results show that the vibration intensity of the block in the x-axis direction is the largest， and that the MEEMD algorithm can suppress modal mixing compared to the EMD algorithm， which helps to better identify the vibration excitation of the block. Key Words： Low-speed diesel engine; Vibration; Signal processing; Modified ensemble empirical mode decomposition

柴油机零部件众多，振动激励源复杂[1]。特别是二冲程低速柴油机具有独特的十字头总成，其振动比四冲程柴油机更复杂。因此，有必要对低速柴油机机体的振动信号进行研究分析。

经典算法包括傅里叶变换和小波变换等[2]。经验模态分解（EMD）算法能够对信号进行自适应分解，避免了傅里叶变换和小波变换依赖窗函数进行分析的缺点[3]。然而，EMD分解结果中存在模态混叠和伪分量[4，5]。为了减少EMD的缺点，改进的集合经验模态分解（MEEMD）算法被提出[6]，并已成功应用于各个领域。如对行星齿轮箱的振动信号进行分解[7]，可滤除包含主要故障信息的固有模态函数（IMF）分量[8]。MEEMD 算法也被用于地震分析[9-10]，研究地震波的变化特征。

上述研究结果表明，MEEMD 算法通过重构本征模函数，具有有效特征识别的可靠方法。然而，尚未应用于船舶低速柴油机缸体的振动分析。因此，本文将MEEMD算法应用于船用低速柴油机缸体振动分析。主要目的是评估该方法在分解低速发动机机体振动信号中的有效性。

1材料和方法

1.1船用低速柴油机

在 MAN B&W 公司生产的一台二冲程低速柴油机上进行了试验研究。该发动机通常用于大型船舶，型号是6S35ME-B9，额定功率3570kW，额定转速142rpm。

1.2信号采集

通过3轴振动传感器，测试机体表面振动信号，安装位置位于3缸和4缸之间，三个轴向（x，y，z）信号被传感器同时采集。

振动传感器测得的信号被传输到数据采集系统，最后通过通用串行总线端口传输到便携式计算机。然后，通过安装的 MATLAB 软件对数据进行离线处理。为了分析发动机机体在中低负荷下的振动情况，在25%负荷（98r、91.64kN.m）、40%负荷（105r、1116.13kN.m）、50%负荷三种负荷工况下进行了试验。

1.3均方根（RMS）

为了评估发动机机体在三轴上的振动强度，利用式（1）计算振动信号的均方根（RMS），

其中是时域信号中的第 k 个加速度值，N表示信号采样的总数。

1.4修正集合经验模态分解（MEEMD）

MEEMD是在EMD基础上，在原始信号中加入一对正负白噪声，利用置换熵算法（PE）去除异常本征模态函数（IMF），以获得更好的分解效果。MEEMD 算法的具体步骤如下。

（1）在原始信号中加入正负白噪声和：

式中表示白噪声的幅度，和是在原始信号中加入白噪声的结果。

（2）应用EEMD对上述信号进行分解，

其中和是EEMD的结果。

（3）对分量进行求和平均计算，最大限度的消除白噪声，得到，

（4）采用PE算法判断是否为异常分量，PE算法定义为式（7），

式中g为PE重构后内部向量的序列，为每个序列发生的概率。

（5）从原始信号中去除异常分量。

（6）最后对r（t）进行EMD分解得到最终的IMF分量和残差：

（7）MEEMD的分解过程可简化为式（10），

2 结果和讨论

2.1时域分析

由图1可以看出，不同负荷下，机体振动表现出不同的强度，三个方向上的加速度均方根值相差很大。值得注意的是，发动机机体的x轴振动最大，且大于z轴振动。一般情况下，由于 z轴是发动机活塞往复运动的方向，缸内燃油燃烧的冲击使得z轴具有较大的振动强度。然而，二冲程低速柴油机的活塞连杆部分的结构不同于四冲程循环发动机，十字头总成是其独特的结构。十字头总成的作用是连接活塞和连杆，承受侧向推力，并指导活塞的运动。在所获得的发动机机体振动中，虽然活塞运动方向的振动强度较大，但由于十字头组件在测量位置产生的侧向推力的存在，x轴的均方根值最大。

随着载荷的增加，z轴振动强度变化不大，y轴振动强度呈增长趋势，约增长90% 。相反，x轴的振动烈度有一定程度的下降，尤其是在50% 载荷工况下，下降了41% 。总体而言，3个方向的均方根值之和在25% 载荷工况下最大，在50% 载荷工况下最小。这表明随着低速柴油机转速的提高，各方向的振动强度趋于一致。

由于x轴的振动强度最大，且与横梁产生的侧推力直接相关，因此对x轴的振动数据进行了分析。图3给出了不同载荷条件下x軸振动的时域波形。与上述分析结果一致，25% 载荷下的振幅较大，最大值为22 m/。然而，40% 和50% 载荷工况下的最大振幅有所下降，下降了27% ，均在16 m/左右。

2.2 MEEMD 分析

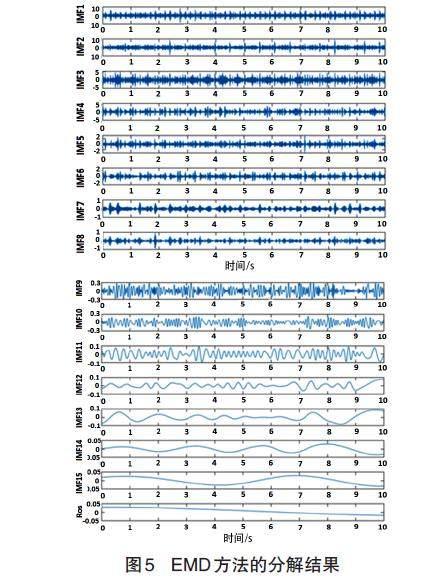
船用低速柴油机不同负荷条件下x轴的时域信号如图2-图4所示。分别用 EMD 和 MEEMD 两种方法处理x轴上的信号，图2-图4的处理结果如图5和图6所示。EMD的分解结果包含15个本征模态函数和1个残差，MEEMD 的分解结果包含12个本征模态函数和1个残差。

EMD 方法的分解结果如图5所示， imf 1-imf 8是具有明显周期性瞬态激励含量的分量。因此，可以假设这些部件是由十字头总成在活塞行程反转期间撞击缸体的激励和气缸内的燃烧爆发冲击引起的。Imf 9-imf 11可以被认为是低速发动机机体的整体振动。其余部件包括 imf 12-imf 15均为稳态单自由度振动。低频成分也可以认为是由低速柴油机的整体振动引起的。最终残差是单调的，不能进一步分解的成分。

MEEMD 方法的分解结果如图6所示，imf1-imf5是具有不同点火周期的信号组件，因此与侧推力和燃料燃烧爆发压力有关，并且比 EMD 少3个。Imf6-imf8是发动机机体的高频振动，而 imf9-imf12是其低频振动。最后，MEEMD 分析的残差是单调的，不能进一步分解，分解结果中白噪声的残差接近于0。因此，在原始信号中加入正负白噪声对各 IMF 分量基本没有影响。该算法也改善了其分解结果。总的来说，改进的经验模态分解的本征模态函数比经验模态分解的本征模态函数少3个，从而抑制了模态混叠，减少了伪分量。该方法在机体振动分析中具有良好的实用性，可为今后低速柴油机机体振动信号处理提供方法参考。

3结论

本研究测量了二冲程低速柴油机在三种不同负荷条件下的机体振动。主要目的是研究柴油机机体振动的剧烈程度及其机理，以及机体振动信号经验模态分解对机体振动信号分解的影响。为此，测量了发动机3个方向（x、 y、 z 轴）的振动信号。结果表明，由于十字头总成产生的侧向推力，x轴上的振动强度最大。与经验模态分解相比，经验模态分解的本征模态函数个数较少，能够抑制模态混叠，减少伪分量的出现。因此，该方法适用于低速柴油机机体振动信号的分解。

参考文献

[1]  胡丽 ，何先波， 谭政宇等.基于盲源分离算法的柴油机噪声激励源诊断[J]. 内燃机工程， 2023，44（1）： 27-33，44.

[2]  HUANG N E， SHEN Z， LONG S R， et al. The empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings of the Royal Society a-Mathematical

Physical and Engineering Sciences，1998;454（1971）：903-995.

[3] 蒋佳炜，胡以怀，方云虎等.船舶动力装置智能故障诊断技术的应用与展望[J].中国舰船研究，2020，15（01）：56-67.

[4] 李瑞星，戴莹莹，王润贤等.基于EEMD和SOM的轴承故障诊断[J].机械工程师，2023（1）：4-8.

[5] 周军，李永祥，任佳鹏.基于MEEMD与HT的谐波检测方法[J].电力系统及其自动化学报，2023，35（6）：73-82.

[6] 鄭近德，程军圣，杨宇.改进的EEMD算法及其应用研究[J].振动与冲击，2013，32（21）：21-26，46.

[7] 魏秀业，程海吉，贺妍等.基于MEEMD与相关分析的行星齿轮箱测点优化[J].制造技术与床，2022（2）：121-125.

[8] 张程，刘佳静，蔡思静等.基于MEEMD与MP的电网低频振荡模态识别[J].智慧电力，2022，50（4）：89-95.

[9] 余华龙，徐国林.基于MEEMD和时变VARMA模型的地震动噪声清除及基线修正[J].地震工程与工程振动，2022，42（2）：172-180.

[10] 胡泰桓，曾春华，朱道恒等.风暴作用下浅水波浪的MEEMD分析[J].海洋科学进展，2023，41（1）：76-86.