基于正态分布初步探索猪肺部病变评分最小采样数量

方杰 肖海君 谭涛

摘  要：在屠宰环节猪进行肺部病变评分（lung lesion scoring，LLS），有助于更全面完整地评估和预测猪场呼吸道疾病及其造成的经济损失。评估结果的科学性和准确性一方面取决于评分的方法和流程，另一方面取决于采样是否随机、样本数量是否足够。文章旨在基于正态分布的基本原理，初步探索猪肺部病变评分中所需要的最小采样数量。

关键词：正态分布；呼吸道疾病；肺部评分；最小采样数量

中图分类号：S851.31+3 文献标志码：A          文章编号：1001-0769（2024）02-0116-05

1  正态分布是自然界常见分布规律

所谓正态分布是指某一个数量指标在诸多随机无关联的因素影响下，最终呈现正态分布，用图形表示像一个钟，中间高、两端逐渐对称减少。用一个简单的例子来解释，影响人身高的因素有很多，如遗传、营养、运动、疾病等，而通过分析大量的身高数据后，发现各个年龄段的男性和女性身高数据分别表现出正态分布的特性[1-2]。这一规律的发现是一个漫长的、逐渐发展的过程，最早可以追溯到1733年，De Moivre和Stirling两位科学家通过计算赌博概率问题的思考，偶然间得到了正态分布的数学公式雏形，后来Laplace进一步完善了该公式，建立了第一代中心极限定理——De Moivre-Laplace中心极限定理，当时没有人会把这个数学公式、定理和自然规律相联系。高斯运用正态分布规律，准确地预测了天文学天体出现的时间。人们逐渐在生物、医药、建筑、经济等各个领域都观察到了正态分布特性，并对数学公式、定理进行了持续的扩展和完善[3-4]。为了纪念高斯的伟大创新，德国10马克纸币上仍然印着高斯头像和正态分布图案。

2  猪呼吸道等多种疾病发病情况符合正态分布规律

正态分布这一规律同样适用于分析猪的疾病[5]。加拿大爱德华王子岛大学大西洋兽医学院的Hurnik等[6]研究了当地一家屠宰场的猪肺部病变，对地方性肺炎和胸膜炎进行了简单肺部病变评分，根据每次的评分结果，通过统计学分析分别计算出每次暴发的地方性肺炎和胸膜炎的严重程度，并发现这个计算结果的数值趋向于正态分布；2005年，德國基尔大学畜牧业研究所的Karsten等[7]发现，猪从感染经典猪瘟到具有传染性的时间间隔也呈正态分布；2016年，                                    美国明尼苏达州立大学兽医群体医学系的Kinsley等[8]发现，猪感染口蹄疫后处于亚临床感染阶段的时间也呈正态分布。由于这是一种普遍现象，有的学者会对样本数据进行正态分布验证来判断采样是否合理，并选择合适的统计分析方法[9-11]。

3  如何通过有限样本反映整个群体的信息

在实践中，我们对未知群体的有限次数的采样并不能总是做到近似拟合正态分布曲线，针对不同采样群体大小和抽样数量，出现了t分布检验、F分布检验、卡方分布检验等方法，这些分布都是基于正态分布公式改变了部分参数推导得到的。在Student t分布检验中，当每次抽样数量达到30个及以上时，t分布近似于正态分布。至此我们又回到中心极限定理，经过了多代科学家的努力和完善，该定理在教科书上最终被描述为：从均值为μ，方差δ的总体中，抽取样本容量n的随机样本，当n充分大时（通常要求≥30个），样本均值的抽样分布近似服从均值为μ，方差δ/n的正态分布。这个定理告诉我们，对于符合正态分布规律的大数据样本，采样数越大就越能反映样本总体的信息，同时应尽可能让每次抽样的数量达到30以上[4]。

4  肺部病变评分中采样数量与正态分布拟合度关系的模拟试验

在开展肺部病变评分时，我们会对每次肺部病变评分中多个肺脏得分数据进行统计学计算得到一个实变指数，范围为0～6，根据这个范围，我们接下来将用R语言去模拟采样数量和正态分布的拟合度关系，以便验证每次采样数量达到30个以上是否必要。基本思路是，使用Set.seed（789）语句固定随机序列，然后按照样本数生成0～6范围的符合正态分布的随机数，由此生成的随机数相当于我们每次肺部病变评分后得到每个肺脏数据，生成一次随机数相当于做了一次肺部病变评分，生成500次就相当于做了500次肺部病变评分。最后，我们比较在样本数量不同和肺部病变评分次数不同的情况下，数据与正态分布曲线的拟合度。

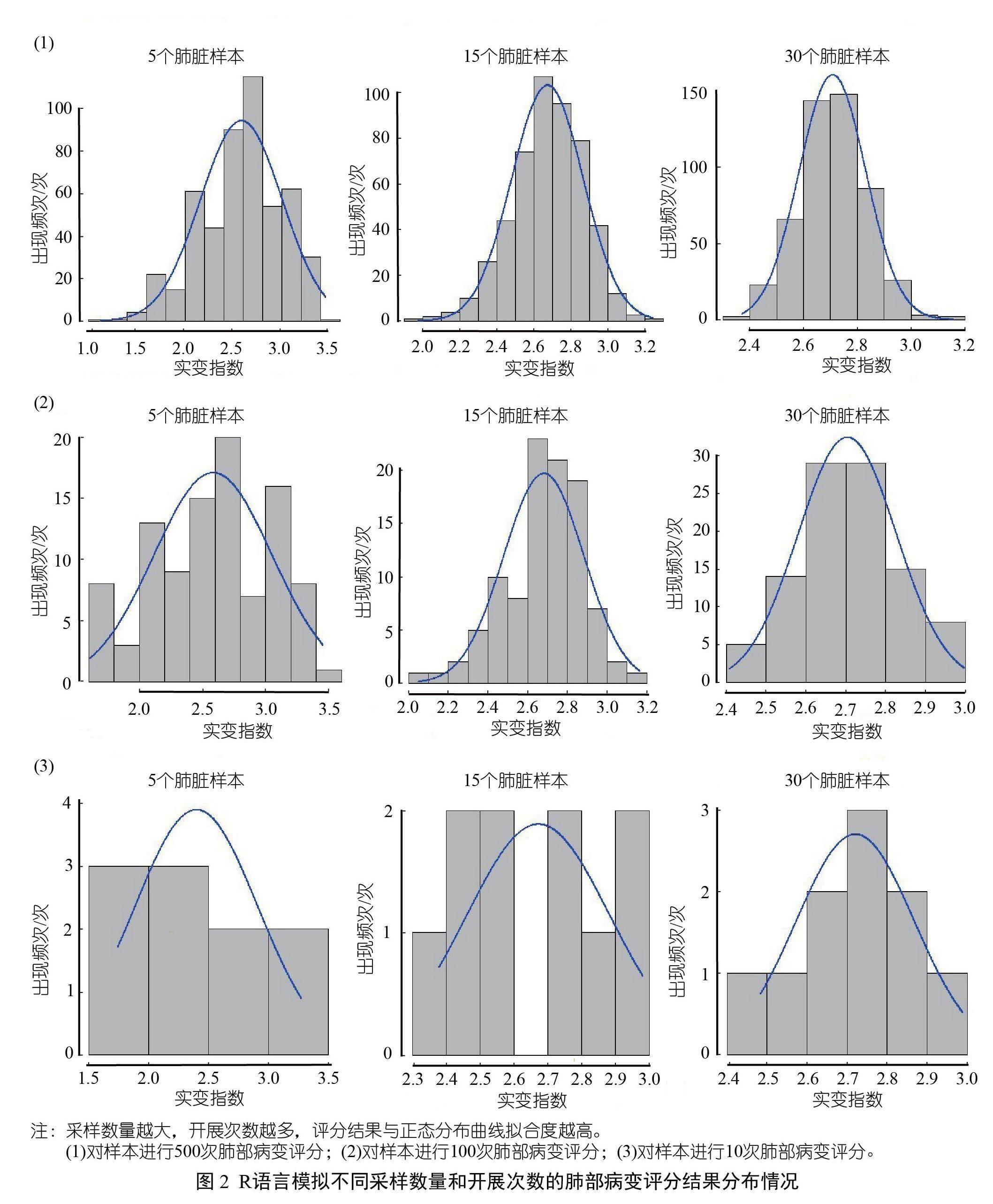
为了方便理解，将代码简化，并以每次采样30个肺脏，做了500场肺部病变评分的模拟分析代码作示例（图1），通过调整n和m的参数获得图2中的9个直方图（图2）。

结果显示，在采样数量较少（每次5个肺脏）的情况下，进行10场肺部病变评分的结果与正态分布差异较大；随着开展场次的增加，情况略有改善，但在该情况下即使开展500场的肺部评分，所得结果也不能较好地拟合正态分布曲线；在采样数量为每次15个肺脏的情况下，10场肺部病变评分的结果依然与正态分布差异较大，开展了100场后，情况有所改善，当开展500场后所得结果已经与正态分布曲线拟合较好；在采样数量为每次30个肺脏的情况下，完成10场肺部病变评分的结果与正态分布曲线的拟合情况已经远远优于5个和15个采样数量，开展了100场肺部病变评分后，已经能较完美拟合正态分布曲线（图2）。

5  从肺部病变评分实践数据中探索正态分布和采样数量的关系

截止2023年7月底，我们在全国开展了134场次猪肺部病变评分，大多数采样数量在30个以上，但也遇到特殊情况造成采样数量不足的，在这种有限的采样数量和开展次数中，我们尝试去进行一些分析比较。考虑到需要在同等开展次数下比较样本量差异的影响，我们在样本量20以下的、样本量20～29的和样本量30以上的肺部病变评分活动中各选择28场次进行正态分布分析。结果显示，从直方图上样本量30以上的结果更趋向于正态分布，20～29样本量略差，0～20样本量几乎不表现正态分布趋势；从RJ（Ryan-Joiner，RJ）指标看，该值越接近1则与正态分布曲线拟合度越高，也是随着样本量增加而更接近1（图3）。

6  結果与讨论

模拟分析结果表明，当开展肺部病变评分次数不足时，尽量需要采样30个以上肺脏才能得到对猪群有代表性的分析结果；当开展的次数足够多时，每次采集15个样本也可以达到近似效果。然而，在实践中，尽管我们期望肺部病变评分是持续开展的；但是，在国内当前情况下，某一家猪场想要持续开展100场甚至以上的肺部病变评分是有一定难度的；在实际屠宰环节，因为各种各样的原因影响样本采集数量，但每场肺部病变评分要尽量采30个以上肺脏样本是非常关键和必要的。

参考文献

[1] BURMASTER D E，MURRAY D M．A trivariate distribution for the height， weight，and fat of adult men[J]．Risk Anal，1998，18（4）：385-389.

[2] 刘海花．大连地区健康成年人人体测量指标的调查[D]．大连：大连医科大学，2011.

[3] 陈希孺．数理统计学简史[M]．长沙：湖南教育出版社，2000.

[4] 李金昌．神奇的正态分布[J]．中国统计，2020（9）：28-30.

[5] PASMA T．Spatial epidemiology of an H3N2 swine influenza outbreak[J]．Canadian Veterinary Journal La Revue Vétérinaire Canadienne，2008，49（2）：167-76.

[6] HURNIK D，DOHOO I R，BATE L A．Types of farm management as risk factors for swine respiratory disease[J]．Preventive Veterinary Medicine，1994，20（1/2）：147-157.

[7] KARSTEN S，RAVE G，KRIETER J．Monte Carlo simulation of classical swine fever epidemics and control Ⅱ．Validation of the model[J]．Veterinary Microbiology，2005，108（3/4）：199-205.

[8] KINSLEY A C，PATTERSON G，VANDERWAAL K L，et al．Parameter Values for Epidemiological Models of Foot-and-Mouth Disease in Swine[J]．Frontiers in Veterinary Science，2016，3：44.

[9] SHEN H，WANG C，MADSON D M，et al．High prevalence of porcine circovirus viremia in newborn piglets in five clinically normal swine breeding herds in North America[J]．Preventive Veterinary Medicine，2010，97（3/4）：228-236.

[10] KWAK S G，KIM J H．Central limit theorem： the cornerstone of modern statistics[J]．Korean Journal of Anesthesiology，2017，70（2）：144-156.

[11] ISLAQM M R．Sample size and its role in Central Limit Theorem （CLT） [J]．2018.