基于粒子群算法的湘江船闸闸室编排算法

邓伟 熊浩奇 余绍军 颜淑婷

摘要：随着水运交通的不断发展，船闸作为重要的水利工程设施，在调节和控制船舶通行方面发挥着关键作用。合理且高效的船闸闸室编排对于提高船舶的通过效率具有至关重要的作用。该研究将粒子群算法引入船闸闸室编排问题中，将每个粒子视为一个可能的船闸闸室编排方案。通过不断的迭代优化，粒子群算法能够寻找到最优的编排方案，从而使得船舶的通过时间达到最短。文章提出的算法能够有效地提高船舶的通过效率，优化船闸闸室的利用，具有实际应用的潜力和价值。

关键词：船闸闸室编排；粒子群算法；编排问题

中图分类号：TP311        文献标识码：A

文章编号：1009-3044（2024）09-0012-03

开放科学（资源服务）标识码（OSID）

1 绪论

船闸作为水运交通中的重要设施，对于船舶的顺利通过和水运运输的顺畅进行起着至关重要的作用。船闸闸室编排是指根据不同船舶的尺寸、通过时间等因素，合理安排船舶在闸室中的顺序和位置，旨在提高闸室利用率和船舶通过的效率[1]。然而，随着船舶规模和运输需求的不断增加，传统的船闸闸室编排方法已经难以满足实际需求，因此需要寻求更优化的算法来解决该问题。本论文的研究目的是基于粒子群算法（PSO） 提出一种优化的湘江船闸闸室编排算法。该算法将通过数据分析和数学模型的建立，与粒子群算法相结合，以求得最优的闸室编排方案。

2 船闸闸室编排的数学模型

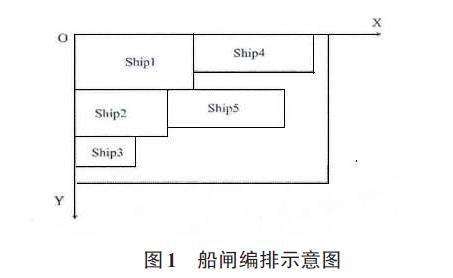
本文将船舶简化为小矩形，因此船舶编排的过程可以简化为小矩形填充大矩形的过程，即在编制计划内填船（排挡），如图1所示[2]。在计划编制船舶时，船舶是否被选中以及选中后所处的位置都会对编排结果产生影响。

为了保证船舶先到先过原则，同时兼顾船舶优先级，通过对船舶综合权重的计算，船舶过闸按综合权重大小进行排序，并生成有序的船舶流。文中符号定义：i，j为船舶编号；xj为第i艘船舶以O为原点在船闸的停靠横坐标；yi为第i艘船舶以O为原点在船闸的停靠纵坐标；ai为第i艘船舶的面积；m为己选船舶总数；n为待选船舶总数；A为船闸闸室面积；L为船闸闸室有效长度；M為船闸闸室有效宽度；leni为第i艘船的长度；widi为第i艘船的宽度[3]。

闸室编排的过程中，由于不同的船舶的进闸组合方案对于平均待闸时间影响不大，因此主要优化闸室面积利用率，闸室编排的目标是最大化闸室面积利用率，如式（1） 所示。

[maxf=i=1maiA]          （1）

选择进入某一闸次的船舶必须满足以下约束条件：

1） 所有选中的船舶能全部排下：

[i=1mai≤A]       （2）

2） 每条选中船舶的尺寸必须小于船闸的尺寸：

[0

[0

3） 所有选中的船舶放置位置不可与其他船重叠，假如船舶j是已选船舶中除i以外的任意一艘，则必须满足：

[xi+leni≤xj]或[xi≥xj+leni]或

[yi+widi≤yj]或[yi≥yj+widi]  （5）

3 船闸闸室编排的算法求解

船舶的配置方法需要考虑排队论，假设所选船闸闸室有m个备选船舶站址，通过估算需要新增n～k（n＜k） 个船舶，可得所有可能的方案有[i=nkCin]个。再进一步根据式（2） 、式（3） 、式（4） 、式（5） 的约束条件，可以筛选出一部分可行的船舶位置优化方案。对上述筛选的可行的优化方案进行计算时，只需要考虑各船舶个数在最小个数和最大个数之间这一约束条件。利用MATLAB进行编程对模型进行求解，具体求解过程如下[4]：

1） 本文将Voronoi图进行左右分块，进行栅格化；确定船舶坐标、船舶最大最小尺寸及船闸闸室容量以及其他相关参数；将船舶坐标、船闸闸室容量利用多维数组进行表示。

2） 将船舶坐标和船闸闸室容量等其他相关参数带入粒子群算法，以最大化闸室面积利用率为主要优化目标，以船闸闸室容量为约束条件，搜索满足约束条件规划方案的最优解。

3） 得到闸室面积利用率，作为粒子群算法的适应度值，记录个体极值和全局极值。

4） 若未达到迭代次数，则更新粒子速度与位置信息作为新的船舶编排方案，重新进行搜索。

5） 若达到迭代次数，则得到最大化闸室面积利用率的编排方案，以数据和Voronoi图进行显示。

利用Voronoi图及粒子群优化算法对模型求解流程如图2所示。

4 闸室面积利用率与待闸时间的优化

在闸室编排的过程中，闸室面积利用率与待闸时间的优化时，最大化闸室面积利用率，如式（6） 所示，平均待闸时间最短的如（7） 所示[5]。

[maxf=i=1maiA]       （6）

[max（m/i=1mbi）]     （7）

闸室面积利用率与平均待闸时间的优化的多目标函数为：

[maxλi=1maiA+（1-λ）m/（i=1mbi）]    （8）

其中：i为船舶编号；bi为船舶i的等待时间；[λ]为权重参数。必须满足以下约束条件还是如式（2） ～式（5） 。

5 算法优越性验证与结果分析

本文利用湘江船闸闸室2023年4月份的闸室使用情况，使用本文提出的粒子群算法得出结果与人工编排进行比较，如表1所示。

如表1所示，使用粒子群算法的船闸闸室容量比使用人工编排高，说明本文的算法具有很高的适应性。

在[λ]=0.5下的湘江船闸闸室利用率和等待时间情况如表2所示。

在[λ]=0.8下的湘江船闸闸室利用率和等待时间情况如表3所示。

如表2和表3所示，使用粒子群算法的船闸闸室容量比使用人工编排高而且等待时间也较人工编排短，说明本文的算法具有很高的适应性。

6 结束语

本文针对湘江船闸的闸室编排问题，提出了一种基于粒子群算法的优化方法。首先对湘江船闸的运行情况和问题进行了调研和分析，包括船舶尺寸、通过时间、闸室容量等。然后，将问题抽象成一个优化问题，并建立了适合粒子群算法优化的数学模型。接着，通过粒子群算法的初始化、迭代更新和适应度评估等步骤，寻找最优的闸室编排方案。最后，通过数值模拟和对比实验，验证了所提算法的有效性和性能优势。

参考文献：

[1] 朱莹莹，王宇嘉.求解复杂旅行商问题的混合粒子群算法[J].轻工机械，2015，33（3）：42-45，49.

[2] 阳琼芳，孙如祥. 粒子群与遗传算法的混合算法[J]. 华侨大学学报（自然科学版），2015，36（6）：645-649.

[3] 李雅琼.基于粒子群算法的遗传算法优化研究[J].兰州文理学院学报（自然科学版），2017，31（1）：55-60.

[4] 汪冲，李俊，李波，等.改进的蚁群与粒子群混合算法求解旅行商问题[J].计算机仿真，2016，33（11）：274-279.

[5] 李擎，张超，陈鹏，等.一种基于粒子群参数优化的改进蚁群算法[J].控制与决策，2013，28（6）：873-878，883.

【通联编辑：代影】