一种基于环振荡器的真随机数发生器

邹小花 李房云

摘要：真随机数发生器（TRNG） 是一种用于生成真随机数的设备，是安全芯片中的重要单元之一，生成的真随机数是确保通信加密及身份认证等密码协议安全性的必要工具。仿真实验结果表明，随着抖动源抖动程度的增大，每次采样的熵趋近于1，即使在最坏的情况下也能达到误差低于10-4的水平。文章进一步分析环振荡器（RO）的数学模型并提出一种基于环振荡器的高效率、低成本的真随机数发生器。

关键词：真随机数发生器；TRNG；环振荡器；RO；抖动源；jitter

中图分类号：TN79，TN918        文献标识码：A

文章编号：1009-3044（2024）09-0008-04

开放科学（资源服务）标识码（OSID）

0 引言

随机数在现实世界中有广泛的应用，比如保障互联网安全的各种加密算法、计算机仿真、电子游戏、抽签等方面。随机数分为两种，伪随机数和真随机数。伪随机数是以数论和计算机理论为基础生成的，实现方便、分布均匀、成本低。由于存在有限的可计算状态，伪随机数具有周期性，使其很容易破解[1]。自然现象或物理过程中的各种随机噪声是真随机数发生器（True Random Number Generator，TRNG）产生随机数的方式。伪随机数存在的周期性问题的解决方法让序列具有了真正的随机性，根据热噪声、闪烁噪声等随机噪声往往都是不可预测和产生的随机数无规律难破解的特点。真随机数发生器产生的随机数存在生成速率相对较慢、随机数的统计特性不好、内外部环境影响的问题。如何设计满足现代加密系统加密需求、具备良好性能的随机数已成为研究的重要问题。关注熵源的设计和优化非常重要，因为熵源的品质从根本上决定着随机数发生器性能的好坏[2]。

梳理国内外相关研究的现状表明，有些科研人员已经实现了根据不同原理结构设计的真随机数发生器。国内科研人员如鲁迎春提出基于可配置异步反馈环形振荡器的真随机数发生器，利用与非门和异或门形成可配置的异步反馈环形振荡器，改善熵源的随机性通过增加相位噪声和扩大时间抖动范围来实现[3]。汪鹏君提出基于压控振荡器的真随机数发生器，通过电阻热噪声放大后作为VCO的控制信号，振荡器中心频率随机抖动[4]。这些真随机数发生器设计方法中有的随机数发生频率太低、有的算法好，但却实现难度大、成本高，有些需要特定的工作环境。基于电路噪声的随机数是不可预测的，具有高安全性。目前基于数字电路的真随机数发生器设计方法有振荡器采样、亚稳态电路等。根据熵源产生随机数的原理[5-8]，以基于环振荡器的真随机数发生器为研究对象，给出了环振荡器RO的数学模型分析，通过在环路中添加多路选择器的方法，使熵源功耗低、體积小、适应性强，最后采用Matlab对模型进行仿真。

1 真随机数发生器设计

真随机数发生器分成三个功能模块：熵源、采样/量化、数字后处理。如图1所示，分别对应产生随机数的三个阶段。

熵源是用来产生原始数据列，这里产生的信号是模拟随机信号。采样/量化是对前阶段产生的随机信号采样和量化，通过D触发器、模拟开关等实现。如果熵源的随机性差或采样电器存在偏置性，后处理单元会对采样量化后的数字序列进一步处理，保证输出随机数具有良好的统计特性。

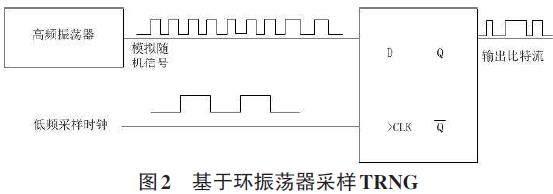
利用振荡器中存在的相位噪声和器件的差异性来产生随机数。基于环振荡器采样TRNG如图2所示。至少需要两个频率不同的振荡器，高频振荡器的信号采样通过D触发器完成，采样时钟是低频时钟，熵源是高频振荡器里的时序抖动。实际设计中，高频振荡器的振动频率大于低频振荡器，输出结果具有不确定性。如果存在非随机噪声，这种方法很有效。由于振荡器的时序抖动不足，只对熵源采样是不够的，生成的随机数的统计性不理想，需要在熵源和采样两个单元进行优化。

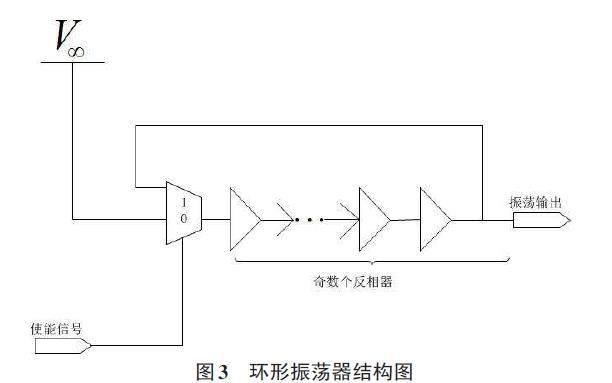
在不同的具体周期上会出现的不可预测的缩短或变长为时钟周期，振荡器的时钟周期在某一个周期上的暂时变化为时钟抖动[9]。振荡器的振荡频率在中心频率附近轻微的无规则变动是时钟抖动在时域上的反映[10]。将奇数个反相器首尾相连并将最后一个反相器的输出反馈到第一个反相器的输入端是采用环形振荡器的结构。 环形振荡器结构图如图3所示。

环形振荡器结构图中的振荡器的时钟信号周期与外部信号没有关系[11-13]，与反相器的门延迟和反相器的个数相关。假设单个反相器的延迟时长为?t，反相器的个数为 N，各个反相器的延迟时长在相同的情况下环形振荡器的振荡周期为：

[T=2*N*Δt]         （1）

通过三个反相器（A，B，C）的例子推导出一个环形振荡器的振荡周期。[T0] 为某一时刻，反相器 A 的输出端（反相器 B 的输入端）在延迟?t后将会变为低电平，反相器 A 的输入端为高电平，则此时t = [T0]+ ?t。

当t =[T0]+ 2?t时，反相器 B 的输出端（反相器 C 的输入端）将变为高电平。

当t = [T0]+ 3?t时，反相器 A 的输入端电平与 [T0]时刻相反，反相器 C 的输出端（反相器 A 的输入端）将变为低电平，通过推导得出从[T0] 时刻开始共需要 6 个?t后完成一个完整的周期振荡。如此反复进行，反相器 A 的输入端再次变回高电平，振荡频率为：

[T=2*3*Δt=6Δt]            （2）

完全由反相器构成的环形振荡器的缺点是功耗相对较大，当不需要随机数发生器工作时，关闭环振，从而降低电路整体的功耗，通过环路中添加多路选择器控制环振[7]。

方案的RO布局说明中，ro_clk中的震荡环完全由奇数个反相器构成，这个震荡环的频率设计为30M左右，即从震荡环起始点经过整个震荡环返回到起始点的这条环路径的延迟设计为15ns左右[14-18]。ro_source中的三十二个震荡环为可控的震荡环，每个震荡环由一个与非门和偶数个反相器构成，三十二个震荡环的震荡频率尽量保持不同，具体配置如表1所示。

2 性能分析

2.1 理想情况分析

在这里，理想情况是指没有jitter的情况，此时整个过程是一个确定性的过程[6]。我们可以看到，32个ro_source一共分为两类：ro_clk的周期15ns是r1～r9、r12、r13、r17、r22、r32（共14个）等于ro的周期的倍数，因此每次采样这些ro的采样结果都是一样的；其余18个ro的周期和15ns不存在整除关系，因此ro的采样结果是不同的，但是对于这些ro来说，采样的结果也只有若干种可能[16]。

2.2 加入抖动后的分析

将一次采样作为一个随机事件来考察，采样的结果[Bout∈{0，1}]。令[xi]表示ri （i=1，2，...，32） ，在此次采样时输出的随机变量，则有[Bout=⊕32i=1xi]，[Bout=1]的概率为

[P（Bout=1）=12+（-2）31?（P（x1=1）-12）?...]         [? （P（X32=1）]    （3）

Xi=1的概率，采用如下记号：

[Ti]：ri的周期；

T：采样周期，固定为150（以0.1ns为单位）；

[T1iTTi]：在一个周期T内，ri采样次数的期望；

[X1=1]：一次采样中ri处在周期[Ti]的前半段；

[X1=0]：一次采样中ri处在周期[Ti]的后半段；

[tio]：ri在采样周期开始时的延迟；

[Jij]：在一个采样周期内，ri在第j个周期的jitter；

[σi]：ri的jitter的标准差；同时满足下述两个条件时，可以认为发生采样时，ri处在第m+1个[Ti]周期内：

[ti0+j=1m（Ti+Ji1）

[T-ti0+j=1m（Ti+Ji1）

满足下述条件时，[X1=1]：

[T-ti0+j=1m（Ti+Ji1）

进一步令[Ji=mj=1Jij]，则有：

[j=1m（Ti+Ji1）=m?Ti+j=1mJi1=m?Ti+Ji]  （7）

其中：[Ji]為m个独立同分布的高斯jitter之和，因此也服从高斯分布，[Ji～N（0，m?σ2i]） 。综上可知，

[P（xi=1）=k=1∞（P（ti0+j=1k（Ti+Jik+1）]

[?P（T-ti0+j=1k（Ti+Ji1）

在jitter值合理的前提下，式（8）中的k值不需要取[1，∞]这么大的范围，假设jitter的标准差为σ，那么只需要[T1i]前后各取[4×σTi]个就够了，并且近似认为式（6）蕴涵式（5），因此式（8）修正为：

[Bout=1]的概率，将（9）代入（3）可以得到[Bout=1]的概率。进一步，按照每个jitter都服从均值为0的正态分布的假设，可以进一步展开表达式。熵分析根据熵的定义，在一次采样中，熵值为：

[Entropy（Bout）=-P（Bout=1）?log2（P（Bout=1））-P（Bout=0）?log2（P（Bout=0））]      （10）

3 数值仿真

TRNG的实验环境由FPGA开发板、外部时钟源以及逻辑分析仪组成。 软件环境为QuartusII 软件进行集成开发。硬件平台是基于 Altera 开发平台的 FPGA 开发板，开发板具有丰富的外围接口，包括PS/2 接口、串口、VGA 接口、网口等。FPGA产生随机数据，逻辑分析采集数据后，检验随机序列的性能。使用Matlab对前述数学模型进行仿真，实验共进行了10次。采样数据如图4和图5所示。

从图4可以看出，随着jitter的增大，P（Bout=1）的概率越来越趋近于0.5，即每次采样的熵趋近于1。Jitter的标准差以0.1ms为单位，P（Bout=1）-0.5的值随jitter标准差的变化而越来越小。振荡器加入抖动的数量直接影响随机源模块产生序列的统计性能，振荡器抖动数量越多，TRNG输出序列的随机性越好。

如果振荡器加入的抖动太多，会消耗过多的硬件资源，功耗也过大。从图5可以看出，即使最坏的情况P（Bout=1）也非常接近0.5，最坏的情况下P（Bout=1）-0.5= 3.69E-05。这个实验结果大大改善了现有真随机数的熵源和采样的方式，提高了TRNG输出的统计特性和随机性。

4 结束语

本文根据熵源产生随机数的原理，提出了一种高速的熵源改进结构。该结构解决了制约随机数发生器输出速率的困难，采取增加振荡器熵源的抖动和轮流采样方式来降低单一熵源的采样速率，输出序列的相关性得到减弱，提高输出序列的随机性。性能分析表明加入抖动后，采样的熵趋近于1，仿真结果表明，重新组合熵源产生的随机数在提高随机数生成速率的同时增强了真随机数发生器的抗攻击能力。

参考文献：

[1] 张鸿飞，王坚，罗春丽，等.基于抖动的高速真随机数发生器的设计和实现[J].核技术，2011，34（7）：556-560.

[2] 周新淳.一位硬件随机数发生器的设计与仿真[J].电子设计工程，2017，25（6）：19-22.

[3] 鲁迎春，韩倩，刘新颖，等.基于可配置异步反馈环形振荡器的真随机数发生器[J].电子测量与仪器学报，2022，36（11）：126-133.

[4] 汪鹏君，李桢，李刚，等.基于压控振荡器的真随机数发生器设计[J].电子学报，2019，47（2）：417-421.

[5] 朱亮亮.真随机数发生器的研究与设计[D].杭州：杭州电子科技大学，2017.

[6] 金杰，罗敏，宫月红.一种基于热噪声的真随机数发生器的设计与实现[J].微电子学与计算机，2015，32（10）：7-11，16.

[7] 赵海英.随机数发生器随机性检测系统的设计与实现[D].成都：电子科技大学，2014.

[8] 董俊，朱文，蒲秀英，等.物理真随机数发生器的设计[J].电光与控制，2013，20（2）：93.

[9] 陳爽，曹素梅，左金印.随机数发生器检测与设计[J].信息安全与通信保密，2012，10（12）：103-105.

[10] 李清，王立辉，刘丹，等.一种基于 Galois 环振的真随机数发生器设计[J].科学技术与工程，2012， 12（17）：4057-4060.

[11] 郭亚炜，邓焕，曾晓洋，等.基于振荡器的真随机数发生器：CN1752924A[P].2006-03-29.

[12] 李艳平.高速时钟信号抖动的ADC测量技术研究[D].成都：电子科技大学，2009.

[13] WIECZOREK P Z，GO?OFIT K.Dual-metastability time-competitive true random number generator[J].IEEE Transactions on Circuits and Systems I：Regular Papers，2014，61（1）：134-145.

[14] 张建国，化腾飞，马荔，等.基于物理噪声源的真随机数发生器的设计与实现[J].机械工程与自动化，2015（5）：1-3.

[15] 张亮，戎蒙恬，诸悦，等.基于混沌系统的真随机数发生器芯片设计和实现[J].上海交通大学学报，2006，40（3）：421-424，430.

[16] 宋勇，陈贤富，姚海东.随机数发生器探讨及一种真随机数发生器实现[J].计算机工程，2007，33（2）：71-73.

[17] 孙曹钧.数字真随机数发生器的设计与实现[D].南京：东南大学，2014.

[18] JOHNSON A P，CHAKRABORTY R S，MUKHOPADYAY D.An improved DCM-based tunable true random number generator for xilinx FPGA[J].IEEE Transactions on Circuits and Systems II：Express Briefs，2017，64（4）：452-456.

【通联编辑：代影】