基于改进A*算法的安全路径规划

杨聿壬 郭江宇 董晓峰 赵阳

摘要：由于传统的A*算法存在搜索角度固定、经过障碍物时过于靠近障碍物、易导致碰撞、转向角度不够平滑的问题，提出一种改进A*算法的安全路径规划方法。对A*算法中的搜索邻域进行扩展，使搜索方向之间的夹角不再局限于45°；基于二维高斯分布设计安全距离矩阵，在启发函数中加入当前节点危险值；采用三次均匀B样条曲线对路径进行平滑处理。经过仿真验证，改进的A*算法能够减少算法迭代次数，提升路径平滑程度，能够有效避免路径存在障碍物，提高了路径的安全性。

关键词：改进A*算法；路径规划；扩展搜索方向；安全距离矩阵；三次均匀B样条曲线

中图分类号：TP301.6     文献标识码：A

文章编号：1009-3044（2024）09-0001-04

开放科学（资源服务）标识码（OSID）

0 引言

路径规划是综合考虑环境和目的地信息，为无人机设计出一条最优的无碰撞行动路线。A*算法作为静态路网中搜寻最短路徑的常用算法，具有搜索性能好、准确度高的优点[1]。在A*算法中无人机通常被等效为栅格中心的一个质点，未考虑无人机本身的体积和机动可能与障碍物产生碰撞。安全路径是在考虑了无人机本身实际大小的情况下，设计出一条与障碍物保持一定安全距离的行动路线，为无人机与障碍物之间留下可以机动的空间，同时避免从障碍物之间狭窄缝隙处通过。

针对A*算法中的不足，国内外许多学者进行不同的改进。文献[2]和文献[3]对A*算法的搜索邻域进行扩展，使得路径的拐点减少，路径总长度变短，路径也更加平滑，能够适应无人机的运动。文献[4]提出稀疏A*算法，通过设置路径的约束条件，裁剪搜索空间中的冗余节点，减少了搜索时间。文献[5]采用球形节点拓展法，基于无人机最小转弯半径和最大探测距离，采用变步长搜索策略，缩短了规划时间，减少了规划步长。文献[6]提出了一种A*波纹减少算法，降低了分辨率的变化造成的路径长度变化的波纹效应，并通过平滑算法的改进缩短了路径长度。文献[7]提出了一种组合式启发函数，采用曼哈顿距离和欧氏距离的线性组合描述距离代价；同时采用双向搜索策略，对传统A*算法进行了优化。文献[8]提出了一种改进A*与人工势场法相结合的算法，将A*算法的解作为引力之一，引入偏航引力增益系数和栅格危险度，提高了路径的安全系数。文献[9]提出一种带四角安全距离矩阵的改进A*算法，但该方法局限于矩形障碍物检测，较小或细长的障碍物在转角处检测效果不好。文献[10]对A*算法子节点扩展方法进行改进，不向障碍物方向进行搜索，该方法局限于扩展节点的8邻域，保持的安全距离固定，缺乏灵活性。文献[11]针对无人机三维空间路径规划，采用自适应搜索方向，缩减搜索空间；重新设计了威胁函数，将威胁空间以概率的形式加入代价函数中。

上述的改进算法在不同程度上提高了传统A*算法的性能，但是并没有很好地解决路径规划中安全距离的问题。当前考虑安全距离的改进A*算法大多仍考虑的是节点的4邻域或8邻域，不能保证更远的安全距离，且避障过程中转向角度固定、转折点过多，不利于复杂环境下规避障碍。针对这些不足，本文提出了扩展搜索方向矩阵，使得改进A*算法的步长更灵活，转向角度不再局限于45°，提高了算法效率；提出基于二维高斯分布的安全距离矩阵，优化启发函数，在选择节点时远离障碍物，同时提出路径危险评估方法，对算法改进前后的路径进行对比评估；采用三次均匀B样条曲线对路径进行平滑处理。

1 传统A*算法

A*算法在Dijkstra算法的基础上，通过添加启发函数来优化代价函数，既考虑了从起点到当前节点的累计代价，又考虑了当前节点到终点的估计代价，从而在保证了搜索效率的同时，又得到了较短的路径。因此，在静态的网格地图路径规划中，A*算法成为求解最短路径的常用算法之一，其启发函数如式（1） 所示：

[f（N）=g（N）+h（N）] （1）

其中，[f（N）]为当前节点的总代价，[g（N）]为起点到当前节点的代价，[h（N）]为当前节点到终点的启发函数值，通常有欧几里得距离、曼哈顿距离、切比雪夫距离三种计算方法。

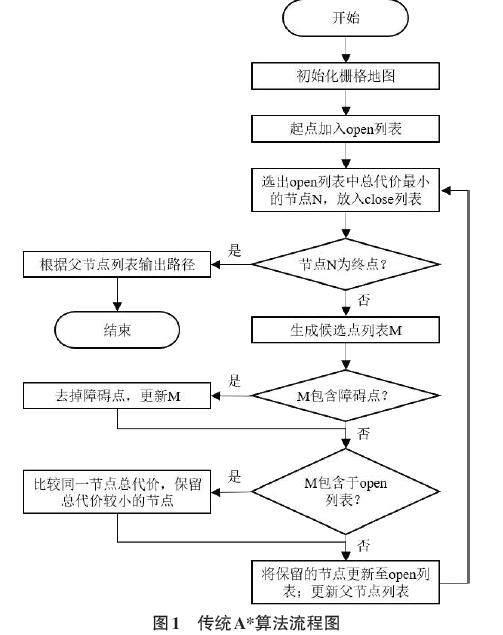
传统A*算法的流程图如图1所示，对其详细说明如下。

1） 采用栅格法构建环境地图，用固定行数和列数的矩阵表示环境地图。矩阵中值为0表示可通行区域，显示为白色；值为1表示障碍物区域，不可通行，显示为黑色。

2） 建立open列表和close列表。open列表用来存储当前点下一步运动的候选节点，close列表用来存储算法计算出的待定路径节点。将起点放入open列表，设置close列表为空。

3） 从open列表中选择总代价最小的节点N，将其移动到close列表。在算法第一轮迭代中，open列表中只有起点，可直接将起点移动到close列表中。

4） 判断选出的节点N是否为终点，如果是终点，则根据父节点矩阵回溯至起点，生成路径，结束循环。如果节点N不是终点，则生成当前点下一步运动的候选点列表M。候选点通常为当前点的4邻域或8邻域。

5） 判断M中的候选点是否在栅格地图中的障碍物上，如果在障碍物上，则从M列表中去除；不在则保留。更新M列表，并计算M列表中各候选点的总代价。

6） 判断M列表中的候选点是否已经存在于open列表中。如果open列表中没有相同节点，则保留；反之，比较候选点在open列表中和M列表中的总代价，选择总代价小的一方更新到M列表中。

7） 将M列表中的候选点坐标及总代价更新到open列表中，同时把当前节点N设置为M列表中各候选点的父节点，记录到父节点列表中。返回步骤3） ，循环至终点被找到。

2 改进A*算法

传统A*算法中，各个搜索方向之间的角度限定在45°，即8邻域内，限制了搜索步长和方向，使得路径搜索不够灵活，也使得路径的转角过大，所得路径并非最优解。同时，在经过障碍物时，路径通常紧贴障碍物边缘，在实际应用中，容易产生碰撞风险。因此，本文采用扩展搜索方向矩阵、安全距离矩阵和三次均匀B样条曲线平滑路径，对上述传统A*算法中的不足进行改进。

2.1 扩展搜索方向矩阵

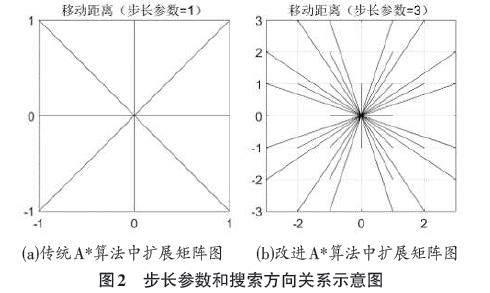
传统A*算法中，当前节点的下一待扩展候选节点通常位于当前节点的8邻域中，如图2中的图（a） 所示。为了扩展搜索的方向，本文采用了如图2中右图的扩展搜索方向矩阵作为待扩展候选节点。图中坐标（0，0） 处为当前节点，最内圈与传统A*算法中的8邻域相同。次内圈的16个节点中，去掉了与最内圈方向相同的8个节点，保留方向不同的其余8个节点。以此类推，可以继续向外侧扩展，矩阵的半径（即步长参数）越大，搜索方向之间的夹角越小，搜索过程就越精准，能够有效减少路径长度和转向角度。由式（2） 可求得不同步长参数对应的搜索方向数。

[S=8×1+R×R-12] （2）

其中，[R]为步长参数，表示当前节点到最远待扩展的候选节点的切比雪夫距离，[S]表示当前节点可以扩展的方向的个数。

2.2 安全距离矩阵和评估方法

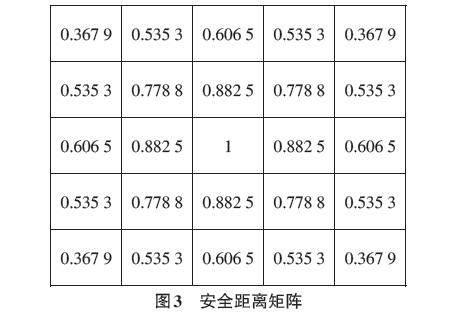
为了计算每个节点的危险值，以该节点为中心建立基于二维高斯分布的安全距离矩阵[MS]，矩阵的每个元素可以由式（3） 求得。

[MS（m，n）=e-12m2+n2a2×b，-d0≤m，n≤d0] （3）

其中，[m]和[n]表示矩阵元素相对于矩阵中心的位置，[d0]表示安全距离阈值，与无人机的机身大小有关，[a]和[b]为比例参数。依照本文仿真实验中的参数设置，[d0=2，a=1，b=2]，可以得到如图3所示的安全距离矩阵。

使用得到的安全距离矩阵，依照图4所示示意图，可以计算出当前节点N的危险值。图中黄色区域为安全距离矩阵的范围，橙色区域为处于安全距离矩阵中的障碍物区域，由于栅格地图中，可通行区域的值为0，障碍物区域的值为1，使用安全距离矩阵中元素与栅格地图对应位置的值相乘，再求和，即可得到节点N的危险值[RiskN]，表达式如式（4） 所示。

[RiskN=xN-d0≤m≤xN+d0yN-d0≤n≤yN+d0MSm，n×MAPm，n] （4）

其中，[MAP]为栅格地图矩阵，[xN]和[yN]分别表示当前节点N的横坐标和纵坐标。

对A*算法中的启发函数[h（N）]进行优化，使其能更合理地反映当前节点到终点的距离估计代价。欧几里得距离为两点间线段的距离，路径规划中起点和终点之间通常都存在着障碍物，因此实际距离比欧几里得距离大；曼哈顿距离为两点横纵坐标之差的绝对值，再求和，类似沿坐标轴方向绕开障碍物的距离，但本文使用的改进A*算法可以沿多个角度的斜线进行路径规划，实际距离比曼哈顿距离要小。因此本文的启发函数为当前节点到终点的加权欧几里得距离与加权曼哈顿距离之和，再加上式（4） 计算出的危险值，更贴合实际距离的同时更倾向远离障碍物的路径，[h（N）]的计算如式（5） 所示。

[h（N）=ω1×EuN+ω2×MhN+RiskN] （5）

其中[EuN]表示欧几里得距离，[MhN]表示曼哈顿距离，加权系数[ω1=ω2=0.5]。

完成路径规划后，需要对整体路径进行危险评估。在路径上等距离取[T]个采样点，计算每一个采样点的危险值并累加，得到路径危险评估值[FR]，计算式如下：

[FR=i=1TRρNi，Nobs] （6）

[RρNi，Nobs=e-12ρa2×b， ρ0，ρ≥d0

其中，[ρNi，Nobs]为第[i]个采样点到最近的障碍物的距离。

2.3 基于B样条（B-spline） 路径平滑

采用栅格地图进行路径规划，计算出的路径通常转弯较多，且转向角度比较大，不利于应用至实际工程中。而B样条路径优化具有几何不变性、仿射不变性等优点，使得拟合曲线与原始路径的差异最小。因此，本文采用三次均匀B样条曲线对A*算法计算出的路径进行优化，将原始路径的所有节点作为B样条曲线的控制顶点，输出经过平滑后的路径。

B样条曲线可以表示为下面的表达式：

[Bsplineu=i=0nPiNi，k（u）] （8）

其中[Pi]为控制顶点的坐标，[Ni，k]是[k]次曲线的B样条基函数，[u]是归一化的非递减节点向量，长度为[n+k+1]。基函数是由节点向量[u]所决定的[k]次分段多项式。

基函数通常采用Cox-deBoor递推公式计算，计算公式如式（9） （10） 所示：

[Ni，0u=1， if ui≤u≤ui+10， others] （9）

[Ni，k=u-uiui+k-uiNi，k-1u+ui+k+1-uui+k+1-ui+1Ni+1，k-1u] （10）

式（9） 为0次基函数，式（10） 为[1～k]次基函数。其中[i]为节点序号，[k]为基函数的次数。

3 仿真实验

为了验证本文提出的改进A*算法的有效性，使用MATLAB 2017a 进行仿真，并与传统A*算法做比较。仿真的地图为[100×100]的规则障碍物栅格地图，本文的改进A*算法的步长参数[R=3]，安全距离矩阵的比例参数[a=2]，[b=1]，安全距离阈值[d0=2]。传统A*算法的步长参数[R=1]，即下一步待探索的候选点为当前点的8邻域，启发函数中不包括危险值。两种方法的对比仿真结果如图5所示。

图中红色路径为使用传统A*算法计算得出，可以看到在图中红色圆圈处，该路径与障碍物边缘十分靠近，甚至从两个障碍物的狭窄缝隙间通过，在实际应用中容易产生碰撞危险。蓝色路径为本文改进A*算法計算结果，可以明显对比出，该路径绕开了障碍物狭窄处，且与障碍物边缘保持一定距离。对两条路径都使用式（6） 和式（7） 提出的安全评估方法，得到的结果如表1所示。

从表1中可以看出，本文提出的改进A*算法在使用安全距离矩阵计算每个节点的危险值并添加到启发函数中后，可以有效避开狭窄通道等危险路径，也可以有效绕开障碍物。但为了保证路径安全，不可避免地需要绕路，导致路径长度略有增加。改进A*算法相比传统算法，迭代次数略微下降，路径长度略微增大了3.76%，但是能够完全避免路径周围2个单元格内存在障碍物，极大地提高了路径的安全性，造成的路径长度提升在可以接受的范围内。

表2中给出了相同的安全距离矩阵参数设定下，改进A*算法选择不同的步长参数时，计算出的路径结果的数据。当[R=1]时，即为传统A*算法只采取安全距离优化，相比传统A*算法，不存在路径碰撞危险，迭代次数只增加了1.26%，但为了绕开障碍物，路径长度增加了7.22%。通过本文提出的扩展搜索方向，随着步长参数的增大，迭代次数和路径长度均减少。但步长参数增大到一定值时，由于两个节点之间距离较大，使得两点间的路径可能靠近障碍物，使路径存在碰撞的危险。

表3中给出了不同安全距离阈值[d0]计算出的路径的对比数据。随着[d0]增大，驱使路径远离障碍物，使得路径长度进一步增大；同时本文的仿真地图较为狭窄，过大的安全距离阈值使得计算危险值时将过多的障碍物内部的单元格计算在内，降低了路径安全的优化效果。因此，安全距离阈值需要考虑栅格地图的障碍物密度，不宜过大。

图6为三次均匀B样条曲线优化对比图，图（b） 中的局部路径比较图为图（a） 中蓝色方框处放大后的示意图。从图中的对比可以看出，优化后的曲线更加平滑。通过计算，优化前的转角总和为396.9°，优化后的转角总和为362.8°，降低了8.59%。

4 总结

本文针对传统A*算法中，搜索角度固定、路径与障碍物碰撞风险较大以及路径不够平滑的问题，对A*算法进行了改进。在选择下一个扩展节点时，引入扩展搜索方向矩阵，使得搜索的步长和方向更灵活；在启发函数中增加安全距离矩阵计算出的节点危险值，使得规划的路径能够远离障碍物；使用三次均匀B样条曲线对计算出的路径进行平滑优化。通过仿真实验表明，改进后的A*算法规划出的路径，安全性显著上升，平滑程度有一定提升，同时算法的迭代次数略微下降。

参考文献：

[1] 路晶，史宇，张书畅，等.无人机航迹规划算法综述[J].航空计算技术，2022，52（4）：131-134.

[2] 辛煜，梁华为，杜明博，等.一种可搜索无限个邻域的改进A*算法[J].机器人，2014，36（5）：627-633.

[3] 张敬寒，陶兆胜，彭澎，等.基于扩大搜索邻域A*算法的平滑路径规划[J].长春理工大学学报（自然科学版），2018，41（6）：124-127，146.

[4] SZCZERBA R J，GALKOWSKI P，GLICKTEIN I S，et al.Robust algorithm for real-time route planning[J].IEEE Transactions on Aerospace and Electronic Systems，2000，36（3）：869-878.

[5] 马云红，张恒，齐乐融，等.基于改进A？算法的三维无人机路径规划[J].电光与控制，2019，26（10）：22-25.

[6] ZAMMIT C，VAN KAMPEN E J.Advancements for A* and RRT in 3D path planning of UAVs[C]//AIAA Scitech 2019 Forum.7-11 January 2019，San Diego，California.Reston，Virginia：AIAA，2019：0920.

[7] 姜月秋，李紫嫣，關启学，等.基于改进A*算法的无人机路径规划研究[J].兵器装备工程学报，2020，41（9）：160-164.

[8] 刘光才，马寅松，齐福强，等.基于改进A～*-人工势场法的城市物流无人机路径规划[J].飞行力学，2022，40（06）：16-23.

[9] 段书用，王启帆，韩旭，等.具有确保安全距离的A*路径优化方法[J].机械工程学报，2020，56（18）：205-215.

[10] 高九州，徐威峰，张立辉，等.基于改进A*算法的无人机避障航线规划[J].现代电子技术，2023，46（8）：181-186.

[11] 卞强，孙齐，童余德.一种新的改进A～*算法无人机三维路径规划[J].武汉理工大学学报，2022，44（7）：80-88.

【通联编辑：梁书】