基于相互学习的短时交通流预测研究

刘忠伟，李 萍，周 盛，闫豆豆，李 颖，安毅生

(1. 云基智慧工程有限公司，广东 深圳 518000；2. 长安大学 信息工程学院，西安 710064)

0 引言

随着城市机动车保有量的不断增加，城市道路日益拥挤。为改善这一状况，交通管理部门提出了利用智能交通系统(ITS，intelligent transportation system)缓解拥堵问题。其中，交通流预测是智能交通系统的核心之一。通过收集历史数据，可以预测未来某个时间段内的交通状况，包括速度、流量和占有率等。根据预测时长[1]，交通流预测可分为短期预测(5～30 min)和中长期预测(超过30 min)。交通流具有明显的时空特性，不同道路之间复杂的空间相关性和时间依赖性给交通流预测带来了挑战。为了解决这些挑战，过去几十年中涌现了许多交通流预测方法。最初，线性回归等统计分析模型被广泛应用，但是统计理论模型属于线性模型，在解决非线性问题时存在不足。受限于统计分析模型的不足，机器学习的发展促使研究者探索支持向量机(SVM，support vector machine)、K最近邻(K-Nearest Neighbors)等基于数据驱动的方法进行交通预测。

1 交通流预测研究现状

近年来，国内外对于交通流预测的方法大致可分为3大类：统计分析模型、机器学习模型和深度学习模型。

1)基于统计分析的预测模型：统计分析模型利用概率论和数理统计等相关数学理论建模，主要有历史平均模型(HA，historical average)[2]、差分整合移动平均自回归模型(ARIMA，autoregressive integrated moving average model)[3]、卡尔曼滤波器(Kalman filtering)[4]等。历史平均模型计算过程简单、速度快，但是模型是静态的，预测的准确性较低。ARIMA模型的主要目标是将时间序列数据转换为平稳序列，以便进行数学建模和预测，因此它对数据平稳性要求较高，主要适用于线性序列预测，但是交通流数据的不平稳性和多种非线性因素可能会降低ARIMA的预测性能。基于统计分析的模型在早期的交通流预测中表现较好，但它们假设交通流是静止的，属于线性预测，仅从概率的角度考虑空间依赖性，实际的交通流受多种因素影响，具有明显的非线性和复杂的时空依赖性。

2)基于机器学习的预测模型：随着交通数据量的急剧增长以及人工神经网络的发展，研究者们开始使用机器学习进行交通流预测，相比于统计分析模型需要手工调参，机器学习模型比较灵活，可以在遍历数据集时可以自动调整参数。常见的机器学习预测模型有：K近邻(KNN，K-nearest neighbors)和支持向量回归(SVR，support vector regression)等。K最近邻算法是选取目标样本所在特征空间K个最近的样本，所选取K个样本数中所占数量最大的类别即为目标样本所属类别。Zheng等人[5]提出了一种改进的KNN模型，在选择K近邻时引入了时间约束窗口并且对状态向量之间距离的局部极小值进行排序，为控制极值的影响，文章在主成分分析基础上，还提出了一种新的分析特征的算法，利用该模型来预测交通流。Hou等人[6]引入了两层KNN算法模型对模式匹配过程做了改进，增加了状态模式匹配使得当前状态向量与历史样本趋势和最小。支持向量机是一种二分类算法，算法思想是求解凸二次规划的最优化。Wu等人[7]应用SVR预测旅行时间，与其他预测模型相比，SVR可以提升预测性能。

3)基于深度学习的预测模型：相比于机器学习，深度学习模型可以更好地挖掘数据隐藏的特性，处理复杂的非线性问题，目前，随着人工神经网络以及深度学习的快速发展，越来越多的研究者将其应用到交通邻域，以其强大的学习能力去提取交通大数据隐藏的时空特性，可以较为准确地预测未来时刻的交通状况。

在提取时间特征方面，循环神经网络(RNN，recurrent neural network)具有较好的性能。Ma等人[8]在真实数据集上利用RNN进行拥堵预测，但是RNN在建模较长序列时会产生梯度爆炸等一系列问题。Qu等人[9]将特征注入RNN，形成Feature Injected RNN (FI-RNNS)，用堆叠的RNN去提取交通数据的序列特征，并将其与上下文因素结合，进一步挖掘交通数据潜在的时间特性。RNN的变体长短期记忆(LSTM，long-short term memory)和门控循环单元(GRU，recurrent neural network)可以有效解决模型训练过程中梯度爆炸等问题，阎嘉琳等人[10]提出基于LSTM的城市交通道路预测模型，并在出租车GPS轨迹数据集上进行验证。Zhang等人[11]考虑了天气因素的影响，使用GRU进行城市交通流预测。

在提取空间特征方面，卷积神经网络(CNN，convolution neural network) 具有强大的特征提取能力。Ma等人[12]提出了一种基于图像的交通速度预测模型，将GPS轨迹数据作为输入，通过矩阵变换将交通路网转化为具有时空信息的图像，图像的两个维度分别表示路网的时间维度和空间维度，然后使用CNN提取图像特征进行交通流预测。Liu等人[13]提出了Conv-LSTM，将卷积和LSTM组合形成一种端到端的结构提取交通流的时空特征，然后使用双向LSTM(Bi-LSTM)提取交通流的周期性特征。但是交通路网是一种典型的拓扑结构数据，将其处理为网格数据后使用CNN，忽略了路网本身的特征，因此研究者们尝试将CNN泛化到图域，形成图卷积神经网络GCN来处理交通路网、社交网络等拓扑结构数据。Li等人[14]提出了一种扩散卷积循环神经网络(DCRNN，diffusion convolutional recurrent neural network)，使用GCN和GRU共同提取交通流的时空相关性，首先在图上使用双向随机游走捕获空间依赖性，然后使用GRU提取时间特征。Yu等人[15]提出了时空卷积网络(STGCN，spatio-temporal graph convolutional networks)，该模型由时空卷积块堆叠而成，利用门控时间卷积和空间卷积提取出最基本的时间特征以及最相关的空间特征。由于GCN强大的空间特征提取能力，研究者们还尝试将注意力机制和Transformer等神经网络与GCN结合来预测交通流。Zheng等人[16]提出了一种图上的多注意网络(GMAN，graph multi-attention network)，由多个注意力模块堆叠而成，包括对空间特性建模的空间注意力模块、对时间特性建模的时间注意力模块以及自适应融合时空特征的门控融合机制。空间注意力机制根据邻近节点对目标节点影响的大小分配不同的权值，时间注意力机制根据预测点历史时刻的影响不同分配不同的权值。Tian等人[17]提出了一种包含时间注意力机制的深度学习网络框架解决城市交通事故预测问题，实现了较好的预测性能。此外，Cai等人[18]将Transformer应用到图上来建模时间相关性，并且设计了4种新的位置编码策略编码时间序列的连续性和周期性。Li等人[19]使用多目标粒子群优化算法优化深度信念网络的一些参数，增强了交通流的多步预测能力。

2 知识蒸馏相关理论

知识蒸馏是一种有效的模型压缩方法，其核心思想是将来自复杂教师模型的知识迁移到简单的学生模型上，从而提高学生模型的泛化能力。教师模型通常拥有较强的预测精度，但其训练过程比较复杂；相反，学生模型参数较少，训练过程较为简单，但其预测能力相对较弱。因此，知识蒸馏技术可以通过教师网络输出的软标签来监督学生网络的学习，从而提升学生模型的预测性能。根据蒸馏的方式和知识类型，知识蒸馏可分为离线蒸馏、在线蒸馏以及自蒸馏。在离线蒸馏中，教师模型经过预先训练，并生成软标签供学生模型使用。基于响应的知识蒸馏、基于特征的知识蒸馏以及基于关系的知识蒸馏则是离线蒸馏中按知识类型划分的3种主要方法。其中，基于响应的知识蒸馏主要侧重于对教师网络最后一层的逻辑输出进行处理，让学生网络去模仿教师网络的输出。2014年Hithon[20]首次提出了基于响应的知识蒸馏，同时也提出了蒸馏温度T的概念，在高温T下，学生网络模仿教师网络的输出，蒸馏温度则是用来软化教师网络的软目标输出，当温度系数值不断增大，得到的输出标签更加平滑。基于特征的知识蒸馏，其核心思想是学习教师网络层与层之间的关系，从而提升学生网络的性能，Romero等人[21]提出的FitNets表示学生能够直接模仿教师网络的特征激活值。基于特征的知识蒸馏可以在学生网络学习时提供更多的信息，但是由于教师网络与学生网络中间层存在维度差异，以及在两个网络上如何选取对应中间层操作较为困难。Park等人[22]提出了基于关系的知识蒸馏，重点关注模型内部特征之间的关系，而不仅仅是模型输出。这种蒸馏方法方法认为捕捉和模仿教师模型内部特征之间的相互作用和依赖关系，可以帮助学生模型更全面地理解任务，从而学到更丰富的知识。

传统的离线蒸馏存在局限性，需要提前训练一个复杂的教师网络，会耗费大量的时间和计算资源，且学生网络不能学习教师网络所蕴含的所有知识，为了解决这些问题，研究者们在传统知识蒸馏的基础上提出了在线知识蒸馏，即无需提取训练复杂的教师模型，教师模型和学生模型在学习过程中互相更新。其中以Zhang等人[23]提出的深度相互学习策略(DML，deep mutual learning)为代表，两个或多个学生模型可以在训练过程中互相学习，互相监督，打破了传统的知识蒸馏预先设定好的强弱关系，无需提前训练复杂的教师模型，将传统的单向知识迁移更新为双向迁移，即训练过程中两个或多个模型互为教师，互为学生。Zhai等人[24]将相互学习策略泛化到图上，提出了图相互学习模型(MGL，mutual graph learning) 将相互学习由规则网格推广到图域。

自蒸馏是一种特殊的在线蒸馏，指在没有新增复杂模型的情况下找到一个教师模型，同样可以提供有效增益给学生模型，意味着教师网络与学生网络应用同一个主体网络，或者直接将自身的信息作为蒸馏损失的监督，是模型内部的知识迁移。2019年，Zhang等人[25]提出了一种自蒸馏的方式，用模型的深层部分蒸馏和监督浅层部分。2021年，Kim[26]等人提出了渐近式自蒸馏(PS-KD，progressive self-knowledge distillation)，用前边几轮的模型去蒸馏后边几轮模型训练。

综上所述，知识蒸馏是一种通过知识迁移和蒸馏损失来提高模型预测精度的方法。这种方法可以满足交通流预测对于精准性的高要求。因此，在本文中，采用知识蒸馏技术对交通流预测模型进行了优化。

3 模型架构

3.1 预测问题定义

交通流预测是根据部署在道路上N个检测器预先收集到的数据来预测未来时刻的交通状况[27]。交通路网可以定义为G=(V，E，W)，其中V为节点的集合，E为两个节点之间边的集合，W∈RNⅹN对应图G的邻接矩阵。实际应用中，节点即为部署在道路上的检测器，收集到的交通信息包括速度、流量、占有率等。对于一个交通网络，Xt∈RNⅹC表示在t时间步交通网络中所有节点的特征的集合，C表示特征的数目。通过给定M0个历史时刻的交通数据去测未来M个时刻内所有节点的交通特征，即交通流预测问题可定义为：

(1)

其中：f(·)是一个经过训练的可学习的函数，可以将历史时刻的交通数据映射到未来时刻。

3.2 DCRNN模型

本文以DCRNN作为基准模型，将交通流建模为有向图上的扩散过程，通过图上的随机游走捕捉交通流的空间特征，使用门控单元GRU提取时间特征，将序列到序列框架和预定采样相结合进行交通流预测。图1即为DCRNN的网络架构，是一种编码器-解码器结构，其中编码器的功能是将一个长度不固定的输入序列转化成一个固定长度的上下文变量，在该变量中编码输入序列信息；解码器将该变量中的信息进行解码生成一个输出序列。

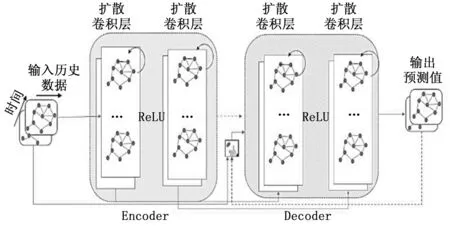
图1 DCRNN模型图

首先对历史交通流数据集按照时间步长进行划分，将路网建模为有向图，图中节点表示部署在道路上的检测器。然后将经过划分处理后的数据作为解码器的输入，解码器由扩散卷积层堆叠而成，以此来提取图中各个节点之间隐藏的空间相关性。使用门控循环单元GRU提取时间依赖性，这是一种具有强大功能的循环神经网络RNN的变体，用扩散卷积代替GRU中的矩阵相乘，产生了扩散卷积门控循环单元DCGRU。编码器的最终输出作为解码器的输入，解码器的结构与编码器类似，进行最终的预测输出。为了解决训练过程和测试过程中输入数据分布不一致的问题，DCRNN在训练过程中采用计划采样，网络将以概率p选择真实值作为下一步的输入，以1-p的概率选择模型自身的输出作为下一步的输入。

3.3 基于相互学习策略的模型优化

DCRNN模型能够有效地提取交通数据中隐藏的时空相关性，并预测未来交通状况。然而，该模型在自身特征感知和提取方面存在一定的局限性。本文受到知识蒸馏中相互学习策略的启发，对DCRNN进行了优化。利用两个或多个网络在训练过程中相互学习，相互协同完成知识的传递，并在不增加模型复杂度的前提下优化模型的预测性能。为了降低训练过程中的参数量，只使用两个未经训练的DCRNN模型构建基于相互学习的预测模型。首先将处理后的数据输入两个模型，分别经过两个模型的softmax层输出预测值，使用KL(Kullback-Leibler Divergence，用于计算不同概率分布之间的差异)散度衡量两个网络预测值的匹配度，KL值越小，则表示两个网络之间的匹配度越高。除KL值之外，使用交叉熵损失(CE，cross entropy)来衡量每个模型的预测值与真实值的差异。综上，在搭建的预测模型中，每个学生网络的损失由两部分组成：传统的监督损失CE以及与同伴网络的匹配损失KL。图2是优化模型DMCRNN(Diffusion Mutual Convolutional Recurrent Neural Network)的结构，其中P1和P2分别表示两个网络在训练过程中输出的预测概率，利用KL(P2||P1)计算两个网络预测概率之间的差异，KL值越小，表示两个预测值之间的差异越小。P1与P2之间KL散度计算公式如下：

(2)

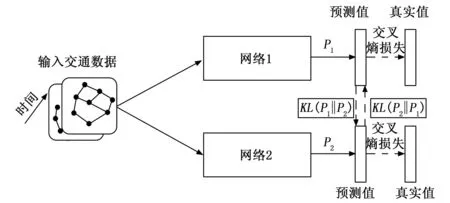
图2 基于相互学习的预测模型

即网络1的损失为相互学习损失以及自身损失以权值系数进行叠加，可表示为：

L1=LC1+DKL(P2||P1)

(3)

同理可得网络2的损失：

L2=LC2+DKL(P1||P2)

(4)

模型在每一次迭代过程中均采用相互学习算法，对DCRNN模型进行优化，两个网络分别利用对方的预测值去更新各自的参数，直至收敛。不同于传统的知识蒸馏为单向蒸馏，即知识仅从教师网络迁移到学术网络，而相互学习是一种双向蒸馏，两个网络在训练过程中不断更新优化，直到参数收敛。基于相互学习的DCRNN模型优化算法框架如表1所示，经过优化后可以提升DCRNN模型的预测性能。

表1 数据集基本信息

4 实验

为了验证基于相互学习算法预测模型的有效性，该研究在两个真实数据集(METR-LA和PEMS-BAY)上进行实验并与其他几种基准模型进行对比。

算法：基于相互学习的交通流预测算法

输入：训练数据，学习率r

初始化：DCRNN网络Net1和DCRNN网络Net2

t=0

do：t=t+1随机抽取数据：

从Net1中计算预测值y1和真实值ytrue；

从Net2中计算预测值y2和真实值ytrue；

计算Net1的随机梯度并更新网络参数：

a.计算误差E1=(y1-ytrue)2；

b.计算Net1的梯度dE1/dw1；

c.更新Net1的参数w1_new=w1-r*dE1/dw1；

更新Net1的预测值y1；

计算Net2的随机梯度并更新网络参数：

a.计算误差E2= (y2-yt rue)2；

b.计算Net2的梯度dE2/dw2；

c.更新Net2的参数w2_new=w2-r*dE2/dw2；

更新Net2的预测值y2

While：目标函数未收敛

4.1 数据预处理

METR-LA：该数据集采样于美国洛杉矶高速公路上的207个传感器，其中包含2012年3月1日到2012年6月7日所收集到的交通速度等信息。数据采集频率为5 min一次，包含34 272条交通数据。

PEMS-BAY：该数据集来源于加州高速公路，包含湾区325个检测器，数据采集频率为每五分钟一次，包含从2017年1月1日到2017年5月31日所收集到的流量、速度等信息，总共有52 116条交通数据。

如表1所示，本文主要使用两个数据集中的速度信息，按照7∶2∶1的比例划分数据集，其中训练集占70%，测试集占20%，验证集占10%。为了提高模型在梯度下降时收敛速度，对数据集采用Z-Score来标准化：

(5)

其中：z表示归一化后的数据，x表示原始输入数据，μ，σ分别表示均值和方差。

构建图的邻接矩阵是交通流预测模型提取空间相关性的关键，DCRNN模型采用基于距离的方法建立图的邻接矩阵，利用交通路网上检测器之间的距离来计算节点之间的紧密程度，加权邻接矩阵计算公式为：

(6)

其中：dist(vi，vj)≤κ，Wij表示两个检测器vi和vj所连接的边的权值，dist(vi，vj)表示vi和vj在路网上的距离，σ表示距离的标准差，k表示阈值。

4.2 实验设置

基于Pytorch框架训练DMCRNN模型，训练时采用内含4张型号为GeForceRTX 3090显卡的服务器，具体的环境配置以及参数设置如表2、表3所示。

表2 硬件条件

表3 实验参数设置

实验过程中利用1小时的历史数据去预测未来1小时内的交通状况。并且训练过程中利用dropout和early stopping机制防止模型过拟合，随机扩散时最大扩散步长为2。

4.3 评估指标

在评估优化后的模型预测性能时，采用如下3个指标评估真实值与预测值之间的差异：

1)平均绝对误差(MAE，mean absolute error)，可以直观显示出真实值与预测值之间的偏差，直观反映模型的预测结果，计算公式如下：

(7)

2)平均绝对百分比误差(MAPE，mean absolute percentage error)，可以评价真实值与预测值之间的符合程度，反映模型预测的准确程度，计算公式如下：

(8)

3)均方根误差(RMSE，root mean square deviation)，可以反映出真实值与预测值差值的变化，反映模型预测的精确程度。计算公式如下：

(9)

其中：n为时间步长，yi和f(xi)分别表示第i个时间步的真实值和预测值，3个指标的数值越小，表示模型的预测精度越高。

4.4 基准模型介绍

为验证优化算法的有效性，我们在两个真实的数据集上进行了实验，并将实验结果与目前具有代表性的7种模型进行了比较。

HA[2]：历史平均模型，即计算历史数据的平均值。

ARIMA[3]：差分整合移动平均自回归模型，一种预测未来值的时间序列分析方法。

VAR[28]：向量自回归模型，可以捕获交通流序列之间的成对关系，是一种更先进的时间序列模型。

SVR[7]：支持向量机模型，利用支持向量机来解决回归问题，是一种线性模型。

FNN[29]：前馈神经网络模型，其中包含多个隐藏层。

LSTM[10]：长短期记忆网络，属于RNN的变体，在长时间序列问题上表现较好。

DCRNN[14]：扩散卷积递归神经网络，利用扩散卷积网络和GRU分别提取空间特征和时间特征。

4.5 实验结果分析

我们在两个真实数据集上进行实验，根据预测结果，利用上述3个评估指标对预测性能进行分析。表4和表5分别展示了DCMRNN模型与其他基准模型在两个数据集上的性能比较，我们选取了15 min，30 min和1 h这3个时间步长进行比较。从表中可以看出本文提出的模型在两个数据集上的3种误差均是最低的，即预测结果更加接近真实值。尤其是随着时间步长的增加，其预测效果更好。从表3和表4中可以看出随着预测时间步长的增加，DMCRNN模型与其他模型三项指标之间的差值越大，表明了该模型在较长时间步预测时仍具有较好的性能，模型具有鲁棒性。在METR-LA数据集上MAE值相较于DCRNN下降了0.15，MAPE下降了0.4%，RMSE下降了0.55；在PEMS-BAY数据集上MAE值相较于DCRNN下降了0.12，MAPE下降了0.2%，RMSE下降了0.31，表明增加相互学习算法后的模型优化效果显著。

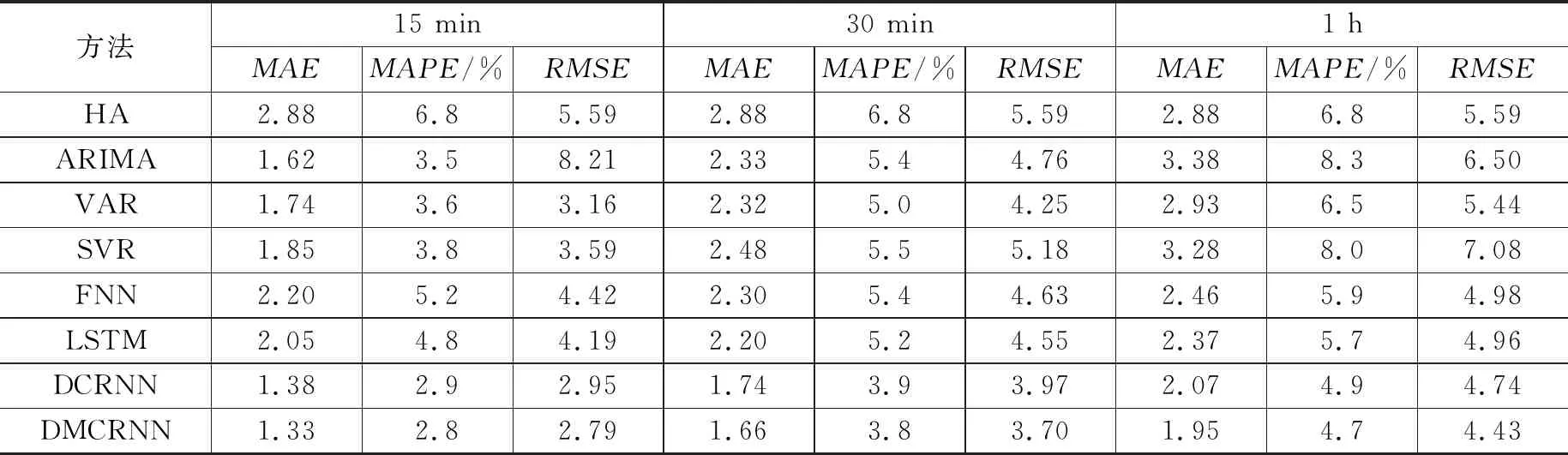
表5 DCMRNN与基准模型在PEMS-BAY数据集上的性能比较

为了进一步比较DMCRNN模型与基准模型DCRNN，

图3、4和5展示了两个模型在METR-LA数据集的3种评价指标以及损失可视化。图3、4和5中灰色线条表示基准模型DCRNN在验证过程中的指标变化，黑色线条表示我们的模型DMCRNN的指标变化，可以看出我们的模型相比于DCRNN，误差可以收敛到更低。图6为两个模型训练过程中损失曲线可视化图，其中我们提出的模型DMCRNN收敛速度更快。图7是两个模型在测试集上RMSE的比较，横坐标表示时间步长，纵坐标表示RMSE，可以看出随着预测时间步长的增加，两个模型之间的差异变大，即我们提出的模型在较长时间步时表现较好。

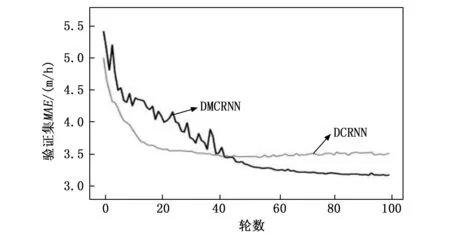
图3 验证集MAE可视化曲线图

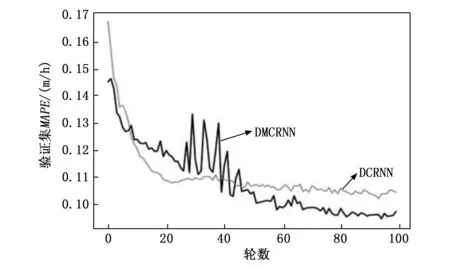
图4 验证集MAPE可视化曲线

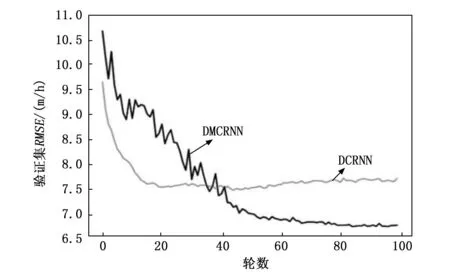
图5 验证集RMSE可视化曲线图

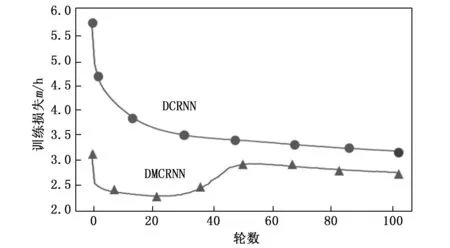
图6 训练集损失可视化

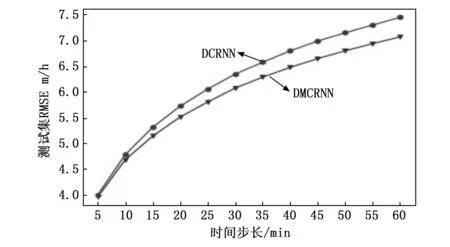
图7 两个模型在不同时间步长上的RMSE比较

4.6 实验参数分析

基于相互学习优化过程中有两个重要的超参数，第一个是不同温度系数对蒸馏结果的影响，第二个是不同的权重系数对两部分损失函数的影响。这两个参数都来源于损失函数，损失函数是模型性能的关键之一，温度T表示蒸馏温度，来源于KL散度的计算过程中，会对网络的性能产生影响；而参数α表示两种损失在总损失中的比重。

实验过程中观察到T=8时验证集上MAE以及损失曲线最终收敛的值比其他温度更低，因此选用T=8作为基准蒸馏温度；将α系数设置为[0.1，0.3，0.5，0.7，0.9，0.99]进行实验，结果显示当α等于0.9或者0.1时，效果最差。α=0.9表示相互学习损失权重过大，网络自身的损失权重过低，极大影响了模型的预测性能。α=0.1表示相互学习损失权重过低，网络之间相互学习能力变弱，同样影响了预测性能。其他3个不同的权重系数对模型的影响整体相差不大，其中α=0.5在验证集上MAE以及损失曲线最终收敛的值较其他两个权重系数的曲线收敛结果更低一点。最终选取α=0.5作为最佳权重系数。

4.7 相互学习可扩展性实验

为了验证相互学习算法的普适性，实验中选取了Shang等人[30]提出的(GTS，graph for time series)模型进行验证，GTS是一种新的图优化方法，当图未知的时候，该方法可学习图结构以增强对多个多元时间序列的预测。GTS也是以DCRNN为基准模型，通过优化图结构从而大幅度提升了预测性能。因此将GTS作为基准模型，增加相互学习算法，使两个GTS网络作为学生模型互相学习。同样在METR-LA和PEMS-BAY两个数据集上进行实验，表7选取了1小时的预测结果进行对比，实验结果可以看出，在增加相互学习算法的GTS模型预测误差相比于原来均有所降低，尤其是在METR-LA数据集上，再次证明了相互学习算法的有效性。

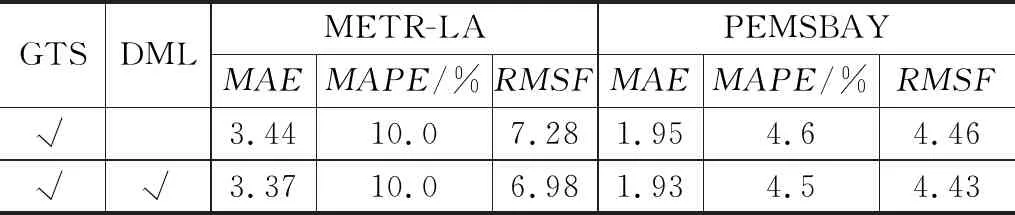
表7 扩展实验结果

5 结束语

本文提出了一种基于相互学习策略的交通流预测优化模型(DMCRNN)。该模型以DCRNN为基准模型，引入相互学习算法，并在两个真实数据集上进行了实验，取得了较好的结果。与其他基准模型进行对比证明了相互学习策略可以有效提高模型的预测性能。同时，设计了扩展性实验验证相互学习在其他模型上的效果，证明了相互学习的普适性。总之，优化后的模型表现良好，但训练过程中会生成两个模型，并联运算，导致训练时间相比基准模型较长，并且会生成两份优化参数。然而，在实际应用中只需要其中一个模型的优化参数。因此，未来工作可以考虑通过优化模型之间的并联方式来减少训练时间。