管道燃气快烤装置燃烧过程数值仿真及结构参数影响分析
柳星河,智小琦,郭 璐,李 劲,贾 杰
(中北大学 机电工程学院,太原 030051)
0 引言
随着军事武器技术的不断发展,现代战场环境日益复杂,武器弹药在保证毁伤效果的同时还要保证在遭受意外刺激时能将引爆的概率和响应程度降低到最小,以减小意外事故对武器平台和作战人员的危害[1-2]。在武器弹药遭受的各种意外刺激中,热刺激是最重要的、最危险的刺激之一,大型武器作战平台遭受的灾害事故中火灾往往占大多数。针对弹药的意外热刺激现象所进行的试验称为烤燃试验,烤燃试验分为慢烤试验和快烤试验,分别模拟了弹药在受到暗火和明火刺激时的响应情况[3-4]。烤燃试验方法、响应机理及影响因素、弹药壳体缓释技术是弹药烤燃研究的主要方向,其中关于影响因素的研究最为广泛且得到了许多有价值的结论[5],而关于烤燃试验方法以及试验装置的研究相对较少。
弹药的快速烤燃试验是评估弹药热安全性的重要标志性试验,大多数意外火灾事故中,弹药都会与火焰产生直接接触从而发生热响应。目前用于快烤试验的火焰源有:池火快烤[6-8]、辐射加热器快烤[9-10]、燃气燃烧器快烤[11-13](喷嘴燃烧器、沙床燃烧器、管道燃烧器)。
大多数快烤试验还是采用航空煤油等有机燃料直接点燃产生明火火烧弹药,该方法简单通用性强,相对也较简单。但也存在一些问题:一是航空煤油燃烧不完全,空气污染非常严重;二是航空煤油池火燃烧温度难以控制,影响燃烧结果;三是航空煤油昂贵,渠道来源受限。而采用清洁的燃气燃烧做火源,给快速烤燃试验提供了一种新的渠道,其优点是燃烧更为充分、污染小,火焰大小可控,且燃气来源便捷。从环境保护和试验效率的角度考虑,使用更为可控更加环保的燃气燃料作为快烤火源未来将成为一种趋势。新版北约的AOP-4240《弹药快速加热测试程序》中已明确提出使用燃气燃料作为火源的快速烤燃试验方法[14],国内目前还没有相应的标准出台。
文献[1]针对开放空间快烤试验过程中燃料不完全燃烧所造成的环境污染问题以及环境风对试验热环境的不可控影响问题,设计了一种可控并且能减少排放污染的封闭式快烤装置,该装置由水冷外壳、受控供气系统和高温加力燃烧室组成。并通过试验对比了开放火焰环境和封闭火焰环境,试验结果表明开放油池火相较于封闭油池火得到的数据更接近实际情况。文献[11]设计了使用液化丙烷气作为燃料的LPG快烤系统,该系统由一个铁支架平台和多个预混火焰燃烧器组成,铁支架平台上水平放置了一面铁丝网用于放置试验产品,火焰燃烧器位于铁网下方,分两列放置,系统的点火和熄灭可以远程控制。进行了三种不同类型产品的快烤试验,测量了产品周围火焰温度并观察了产品响应情况。试验结果表明,以液化丙烷气作为燃料的小型测试设备可以替代航空煤油池火,并且新的试验设备更加环保经济,且易于操作。但是预混燃烧器产生的火焰辐射热流占比较低,且产生的火焰温度环境不均匀。文献[12]设计了丙烷沙床燃烧器,该装置主体为一个矩形铁盘,铁盘大小1 000 mm×1 150 mm,铁盘上表面铺设了一层沙子,侧面设置有燃气管道入口,燃气进入铁盘从上表面沙层流出后燃烧以产生均匀的火焰。采用了平板温度计测量了快烤装置的火焰温度,并与航空煤油池火和预混燃气燃烧器进行了对比。试验结果表明,沙床燃烧器性能位于航空煤油池火和预混燃气燃烧器之间,航空煤油的火焰温度最均匀,平均火焰温度最高,预混燃烧器产生的火焰平均温度最低,且温度环境不均匀。文献[13]在沙床燃烧器的基础上,设计了小型管道燃烧器,试验装置大小1 000 mm×1 150 mm,由10根钻孔管道组成,每根管道都由一个燃气罐供应燃气。试验采用了绝热表面温度探头(ASTP,adiabatic surface temperature probe)测量了火焰环境中的热流密度,试验结果表明,管道燃烧器能满足快烤试验要求的温度均匀性和热流要求,且装置结构简单易于维修更换。小型管道燃烧器适用于迫击炮和中口径炮弹,如果需要测试大型产品,燃烧器等比放大即可。
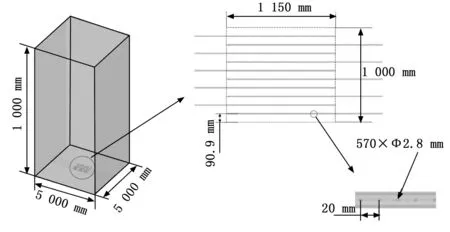
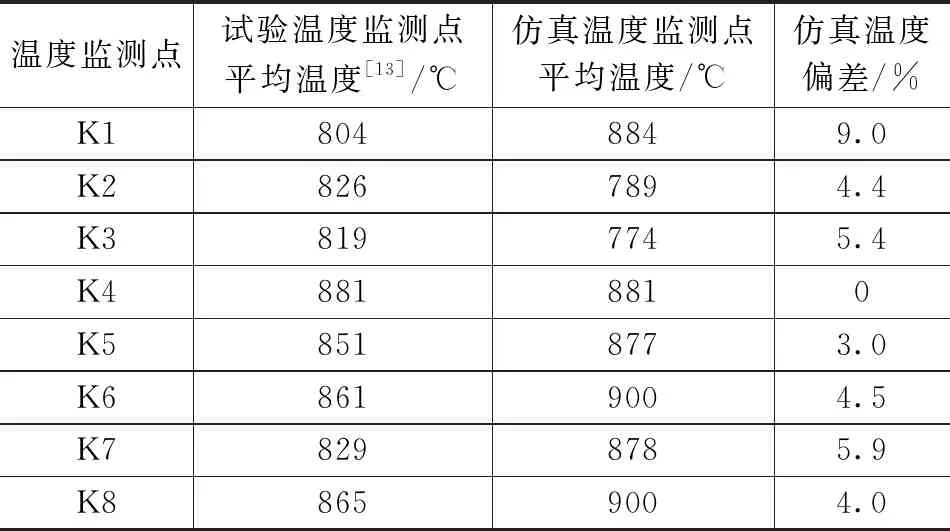
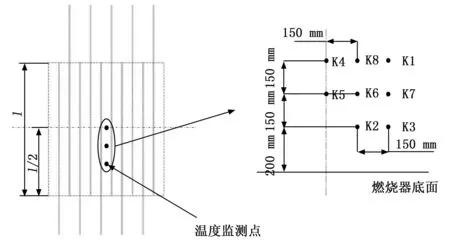
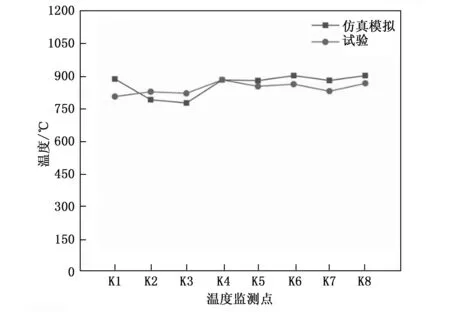
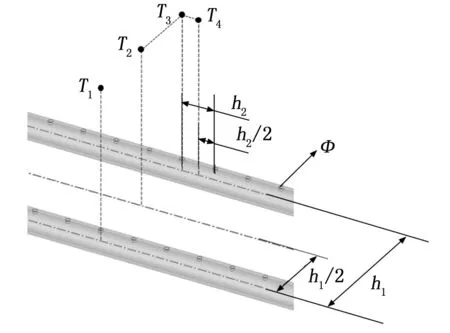
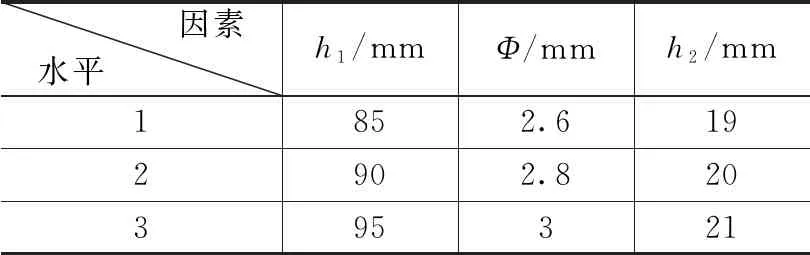
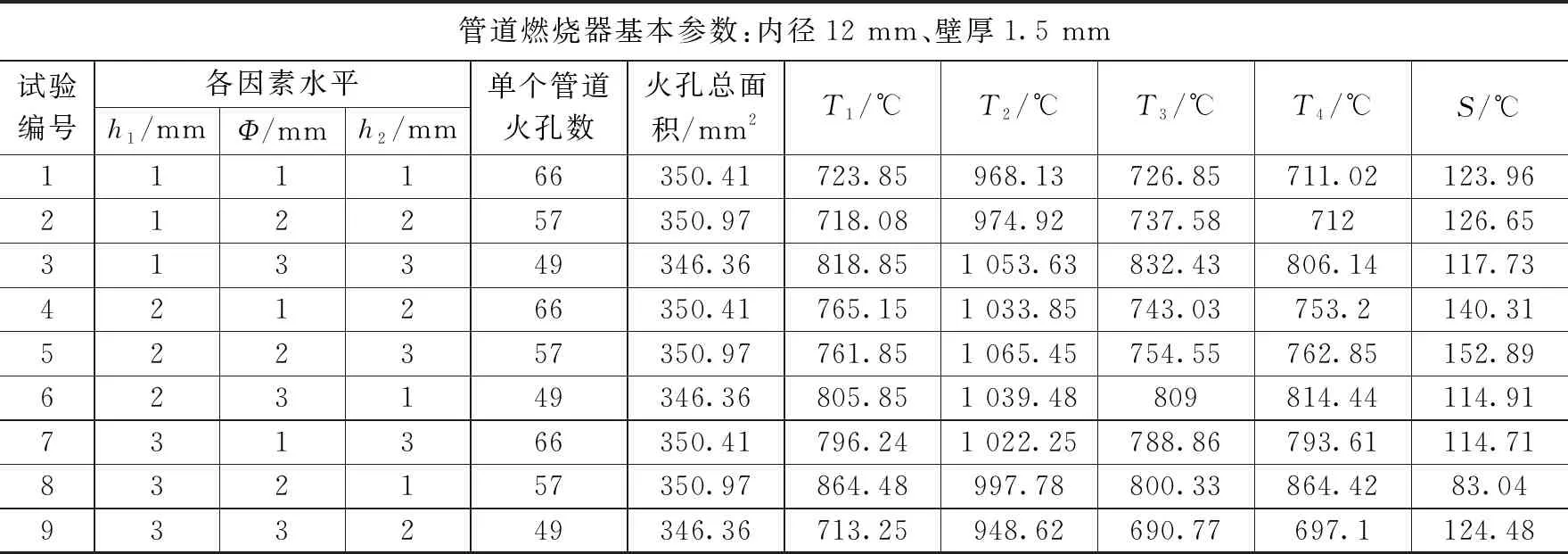
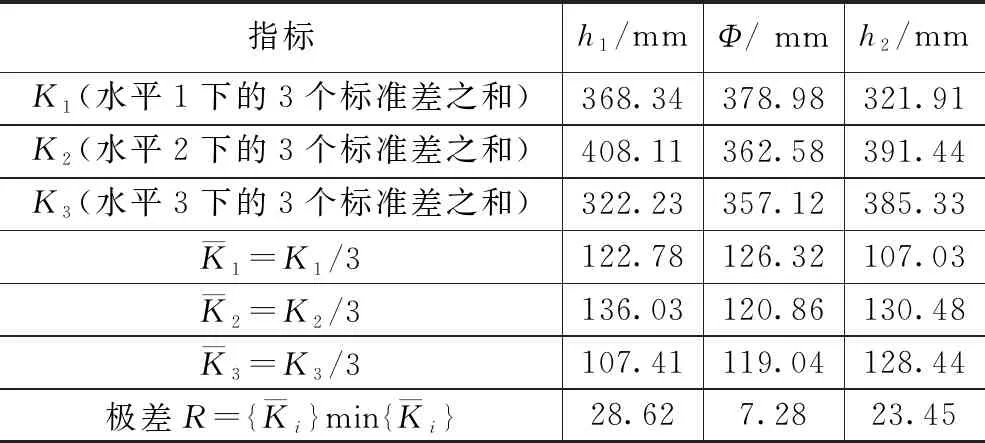
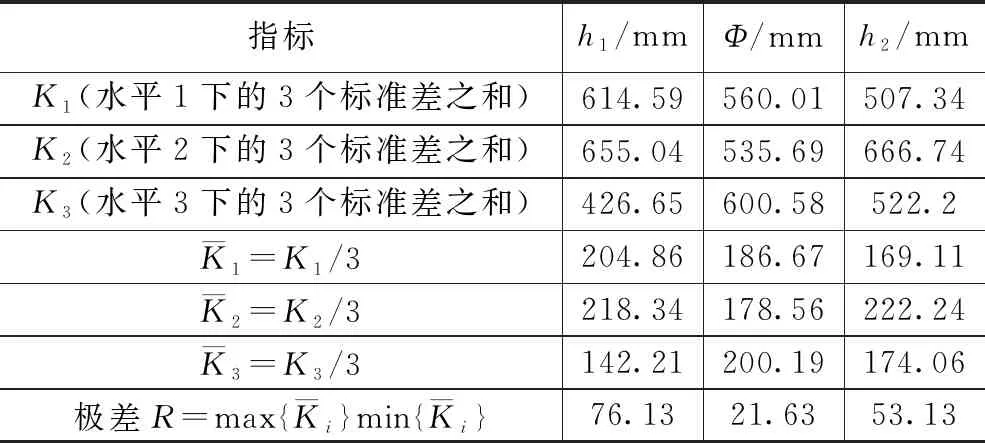
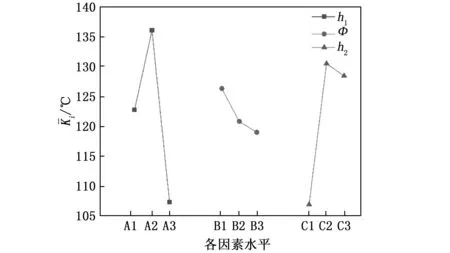
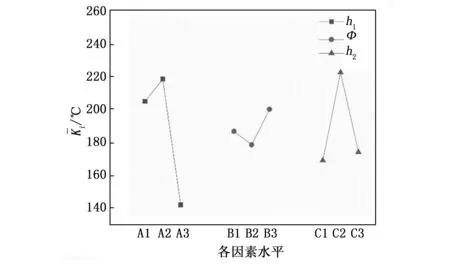
文献[15]设计了密封状态不同的烤燃弹结构,并采用航空煤油为火焰源进行了快烤试验,研究了不同密封条件对于RDX基传爆药快烤响应烈度的影响,定义了间隙系数A来表现壳体的密封程度,间隙系数为泄气面积与药柱表面积的比值,在试验条件下得出:A=0时,响应为爆轰反应;A≥0.014 3时,响应为燃烧反应;0 综上可以看出,国外对于快烤试验方法和试验设备的研究较为系统和全面,并且很早就开始了燃气快烤装置的相关研究。他们的研究着重于燃气快烤装置的设计和搭建,并通过大量试验验证了燃气快烤装置的可行性,即装置产生的火焰特征能否达到航空煤油池火的效果。但对于燃气装置结构参数与火焰特征的关系,以及燃气装置的优化方法还没有进行深入研究。而国内对于快烤试验的研究目前着重于研究弹药的快烤响应等级以及相关数值仿真方法的研究,快烤试验大多采用的还是航空煤油池火,关于燃气快烤试验的研究还鲜有报道。 管道燃烧器制造简单,火焰特征与池火火焰相当,且结构简单便于维修和更换,是目前较为理想的兼具环保性和经济性的燃气快烤装置。国外相关学者已经通过试验验证了管道燃气快烤装置可以达到航空煤油池火的效果,并且国外一些试验测试公司已经将管道快烤装置作为快烤试验的火焰源使用。本文通过CFD与正交试验法相结合的方法,对文献[13]中设计的管道燃气快烤装置进行仿真研究,分析影响管道燃气燃烧火焰温度及其均匀性的关键参数及其影响规律,并在此基础上对文献[13]的快烤装置进行优化设计,提高其使用性能,以期为今后设计和使用燃气快烤装置提供必要的参考。 计算流体力学(CFD,computational fluid dynamics)可以预测流体流动、传热控制、化学反应以及其他相关物理现象。由于物理试验需要大量的人工和经济成本,所以在产品设计初期进行大量的验证试验并不划算,借助CFD软件补充物理试验,可以节约成本,并观测在试验中不易观测的现象,有效降低了研究周期。本文选择商用CFD软件Fluent进行仿真研究。 1.1.1 控制方程 计算流体力学进行流体计算时需要遵循质量守恒定律、动量守恒定律和能量守恒定律,由此可以得到3大方程:质量连续性方程、动量方程和能量方程[18-21]。 质量连续性方程: (1) 式中,ρ为流体密度;u为流体速度。 动量方程: (2) 式中,ui为直角坐标系中的x、y和z方向的速度分量,Fi为单位体积上质量力的分量,μ为动力粘度。 能量方程: (3) 式中,es为单位质量流体能量,P为单位体积表面力,k为热传导系数,在使用能量方程时,一般只讨论机械能之间的转换和求解损失功的大小。 1.1.2 燃烧化学反应模型 Fluent用于模拟燃烧反应的模型有通用有限速率模型、非预混燃烧模型、预混燃烧模型、部分预混燃烧模型以及PDF运输方程模型,其中适用于燃气扩散火焰模拟的有通用有限速率模型和非预混燃烧模型[20-21]。 通用有限速率模型即组分运输模型是基于组分质量分数的运输方程解,其运输方程如式(4),根据所定义的化学反应进行模拟,反应速率以源项的形式出现在组分运输方程中: (4) 非预混燃烧模型是求解混合分数运输方程和两个守恒标量的方程,这样可以从预测的混合分数分布中求解出每一个组分的浓度。通过概率密度函数(PDF,probability density function)来考虑湍流的影响。 非预混模型中混合分数定义如式(5): (5) 式中,Zk为元素k的质量分数,Zk,o为氧化剂入口处k元素的质量分数,Zk,f为燃料入口处k元素的质量分数,f为计算中控制容积内燃料的质量分数。f=0表示已经完全燃烧,f=1表示为开始燃烧。 非预混模型可以通过关于混合分数的方程代替组分运输方程。混合分数的方程如式(6): (6) 式中,μt湍流粘度系数,Sm指质量由液体燃料滴或反应颗粒传入气相中的量,Suser为用户自定义源项。 1.1.3 湍流模型 计算湍流的方法主要有3种,即直接数值模拟法(DNS,direct numerical simulate)、雷诺时均模拟法(RANS,Reynolds averaged Navier-Stokes)以及尺度解析模拟法(SRS,scale-resolving simulate)。DNS就是直接求解完整的三维非定常N-S方程,其对湍流的流动没有做任何假设与简化,理论上可以得到精确的计算结果。但由于湍流的特性,导致采用DNS需要非常大的计算资源,其模型网格最小尺寸要小于湍流的最小涡尺度,才能表现出完整的湍流状态。目前来说DNS方法只能用于简单几何的流动机理研究,还无法用于真正意义上的工程计算。RANS方法是将非稳态的N-S方程对时间做平均,求解工程中需要的时均量。然而平均处理会在输运方程中引入额外的未知项(雷诺应力和通量),使得方程中未知量的个数大于方程个数,需要选择合适的湍流模型进行封闭[22]。SRS方法不同于RANS方法的平均处理,它可以解析出部分湍流信息,其核心思想是对N-S方程进行某种过滤,把小于过滤尺寸的脉动使用模型表达,而大于过滤尺寸的涡则直接求解,从而分辨出更多流动细节。其求解精度与网格分辨率和时间步长关系密切,需要较小的网格和时间步长对湍流进行解析,因此其计算量相对于RANS来说要大很多。 在这3种湍流计算方法中,RANS方法是应用最广泛的湍流模拟方法,Fluent中大部分湍流模型均采用RANS方法。该方法最为典型的模型为k-ω模型,本文仿真模拟中选择的湍流模型为SST k-ω模型,该模型将湍流问题简化为两个附加输运方程的求解,并引入涡流粘度(湍流粘度)来计算雷诺应力。通过求解输运方程获得湍流粘性系数,最终得到的总粘性系数分为层流粘性系数和湍流粘性系数[23],即: μ=μl+μt (7) SST k-ω模型的输运方程为[24]: (8) Gω-Yω+Dω+Sω (9) 式中,Gk为湍流动能的生成,Gω为ω的生成,Гk和Гω为k和ω的有效扩散率,Yk和Yω表示由湍流引起的k和ω的耗散,Dω为交叉扩散项。 在进行产品测试时测试软件主要完成测试环境确认,测试资源的检查和复位;产品供电及工作时序的控制;产品输出信息的接收、存储和实时显示;产品测试项目的检测和判读。测试仪对产品参数进行动态检测的过程中,能够实时显示系统测试状态、测试数据和测试曲线,并直观显示测试的最终结果。 为验证仿真模型的准确性,本文参照文献[13]所进行的管道燃气快烤试验,建立仿真模型,并通过与试验结果的对比来验证所建立模型的准确性。 1.2.1 物理模型 文献[13]中设计的管道燃气装置如图1所示,燃烧器整体尺寸为1 150 mm×1 000 mm,包含10根长1 150 mm,外径Φ15 mm的钻孔钢管,管壁厚度为1.5 mm,管道间距90.9 mm,十根管道上共钻有570个Φ2.8 mm的火孔,火孔孔距为20 mm。每根钢管连接一个燃气罐供应燃气,以确保试验过程中燃气的供应充足。 图1 文献[13]管道燃气快烤装置示意图 根据燃烧器相关参数建立的物理模型如图2所示,为减少边界对于燃气燃烧的影响并模拟开放空间中的燃烧情况,考虑到计算资源,设置空气域为5 m×5 m×10 m。 图2 仿真模型结构尺寸示意图 1.2.2 网格划分 本文仿真过程中涉及管道内流体流动模拟,流体在管道内流动时,因其粘性作用会在管道壁面产生边界层。边界层网格的设定对于管道内流体流动的模拟影响很大,一般通过y+值确定边界层网格大小,其求解公式如下[25]: (10) 式中,uτ为摩擦系数,υ为流体粘度,y为第一层边界层厚度。对于低雷诺数湍流模型(k-ω模型),y+值取1,计算得到第一层网格厚度为3.4×10-3mm。 通过网格无关性验证,综合考虑计算成本和计算准确性,最终选择网格数量为5 640 873个,网格划分采用Fluent Meshing特有的poly-hexcore网格,生成好的模型网格如图3所示。为减少计算时间,仅对火焰区域和管道火孔区域进行加密,火焰加密区网格大小为30 mm,火孔处加密网格大小0.5 mm。 图3 模型网格划分 图4模型边界条件设置示意图 1.2.3 燃烧模型和辐射模型 本文选用非预混燃烧模型对燃气火焰进行模拟。气体燃料选择为丙烷,丙烷物性参数如表1所示。本文在计算时选择的辐射模型为P1辐射模型。 表1 丙烷物性参数 1.2.4 边界条件 根据燃气燃烧的实际情况,模型中定义的边界条件有燃气入口边界、空气入口边界、出口边界、壁面边界。整个燃烧装置中包含10根燃气管道,每根燃气管道与空气域的交界设置为燃气入口,入口类型为质量流入口,入口流量为0.004 kg/s。空气域四周设置为空气入口,入口类型为速度入口,设置入口速度为0.05 m/s。空气域上表面设置为压力出口,出口表压为0 kPa,下表面设置为绝热壁面边界,模拟地面。燃烧过程中忽略火焰对管道壁面的传热影响,设置管道壁面为绝热壁面。仿真中环境温度为300 K,环境压力为101.325 kPa。 1.2.5 求解设置 本文仿真模拟采用压力基瞬态求解,求解算法选择压力和速度耦合算法,时间步长设置为0.5 s。当迭代步数达到设定值即停止计算。观察火焰温度监测点的变化曲线,如果火焰温度波动趋于平稳,出现温度平台,则可以认为模拟已收敛。 为验证仿真模型的准确型,按照文献[13]中燃烧试验设置的温度监测点位置,在仿真模型中设置相同的8个温度监测点,各测点位置分布如图5所示。通过对比仿真和试验中各测点的平均温度,验证仿真模型的准确性。仿真与试验值比较如图6所示。试验温度测点数据和仿真所得到的各测点温度及误差如表2所示。 表2 试验和仿真温度数据表 图5 温度测点布置图 图6 仿真与试验数据对比 从仿真测得的8个测点温度和试验的对比表中可以看出,K1点的温度偏差最大,偏差为9%,其余点均小于6%,各测点温度误差均不超过10%。从仿真与试验的测点温度变化图可以看出,仿真与试验结果基本吻合,验证了所选模型的准确性。 北约标准化协议AOP-4240中要求快烤火焰要保证烤燃试件的周围热空间均匀性,并且30 s内温度要达到550 ℃,火焰稳定后的平均温度不能低于800 ℃[14]。所以燃气快烤装置不仅要保证试件周围火焰温度不低于800 ℃,且燃烧器上方火焰温度的均匀性也是判断燃气快烤装置的重要指标。为保证管道燃烧器空间温度及其均匀性,设计了正交试验,通过仿真研究管道参数对燃气火焰空间温度分布的影响。 设管道直径不变,本文选取了管道燃烧器的3个主要参数:管道间距h1、火孔孔径Φ、火孔间距h2作为正交试验的3个因素。燃烧器其他参数保持不变,即管道内径为12 mm,外径为15 mm,管道上火孔出口总面积保持不变。选择燃烧器火焰温度的均匀性作为燃烧器的正交试验的判断指标。 正交试验设计是研究多因素多水平的一种试验设计方法,不同于全面试验对每种情况都进行试验的方法,它根据正交性从全面试验中挑选出部分代表性的点进行试验,这些代表性的点具备了“均匀分配,整齐可比 ”的特点。正交试验设计使用一种规范化的正交表进行试验设计,可以用较少的试验次数,取得较为准确、可靠的优选结论,是一种高效率、快速、经济的试验设计方法。由于管道燃气快烤装置是由多根管道燃烧器组成。为了节省计算资源,减少仿真时间,不考虑火焰间的干扰,对模型进行简化。 选择两根管道燃烧器进行正交试验仿真研究,分别在燃烧器上方0.3 m和0.45 m的平面上,布置4个温度测点,测点分布如图7所示。T1、T3分别位于两根管道火孔正上方,T2位于T1和T3中心,T4位于相邻两个火孔中心。以4个测点温度的标准差作为指标研究火焰温度均匀性,标准差S计算公式如式(11)所示: 图7 温度测点位置示意图 (11) 以S为指标对0.3 m和0.45 m处两个高度平面分别进行计算分析。各因素各水平内容如表3所示。 表3 正交设计各因素水平表 根据设计好的3水平3因素表建立仿真模型。仿真试验中相关设置与上节仿真模型相同。仿真燃烧模型选择非预混燃烧模型,湍流模型选择SST k-ω模型,辐射模型选择P1模型。相关边界条件设置如下:空气入口选择速度入口,入口速度0.05 m/s;燃料入口选择质量流入口,入口质量流为0.004 kg/s,出口选择为压力出口,壁面边界条件为绝热壁面条件。 按照正交试验表设计的工况进行仿真试验,试验结果见表4。根据表4的试验结果,分析管道参数变化对于燃烧器上方火焰温度均匀性的影响,并得出各参数对火焰温度的影响权重,找出最佳方案。 表4 正交试验数据模拟结果 采用极差分析法对各因素水平的影响进行分析,0.3 m和0.45 m高度上各因素的极差结果见表5和表6。极差越大,说明因素的影响越重要。根据极差计算表和指标趋势图分别对0.3 m和0.45 m高度处温度均匀性指标进行分析。 表5 0.3 m高度温度均匀性极差计算表 表6 0.45 m高度温度均匀性极差表 由表5和表6可以看出,不论在0.3 m高度还是0.45 m高度处,管道间距都是影响火焰温度均匀性的最主要因素,其次是火孔间距,最次影响因素是火孔孔径。根据标准差S随各因素水平的变化趋势图(图8、图9),得出在0.3 m和0.45 m处管道参数的最佳组合。在0.3 m高度处火焰温度均匀性的最佳因素组合均为A3B3C1,即管道间距取95 mm、火孔孔径取3 mm、火孔间距取19 mm。在0.45 m高度处火焰温度均匀性的最佳因素组合为A3B2C1,即管道间距取95 mm、火孔孔径取2.8 mm、火孔间距取19 mm。可见,同一燃烧装置结构在不同高度处的火焰均匀性是不同的,表现出最佳方案不同。因此实际应用中,应根据燃烧装置,确定最佳高度,以确保温度均匀性的最佳方案。 图8 0.3 m高度火焰均匀性指标随试验因素变化趋势 图9 0.45 m高度火焰均匀性指标随试验因素变化趋势 为了减少航空煤油池火快烤试验产生的环境污染,提出了使用清洁燃料的燃气快烤装置,管道燃气快烤装置是目前应用最广泛的燃气快烤装置。本文以文献[13]中的管道燃气快烤试验为基础,采用CFD和正交试验法相结合的方法研究了管道燃气快烤装置结构参数对于其火焰特征的影响,并对快烤装置进行了结构优化设计。仿真的得到的各测点平均温度与试验相比误差均小于10%。选择管道间距、火孔孔径以及火孔孔距3个参数,设计了三因素三水平正交实验,分别分析了在管道上方0.3 m和0.45 m处各因素水平对管道燃烧器火焰温度均匀性指标的影响。在本文仿真试验条件下,得出以下结论:在管道直径确定的条件下,管道间距是影响管道燃烧器火焰温度均匀性的最主要因素,其次是火孔间距,火孔孔径是影响火焰温度均匀性的最次要因素。本文研究条件下,在0.3 m高度处火焰温度均匀性的最佳因素为:管道间距取95 mm、火孔孔径取3 mm、火孔间距取19 mm;相同条件下,管道燃烧器上方不同高度处火焰温度均匀性对应的最佳结构参数并不相同。试验时根据试件的放置高度,有不同的最佳结构参数。1 数值模拟
1.1 数学模型
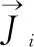
1.2 物理模型建立及仿真设置



1.3 仿真模拟结果验证
2 管道燃烧装置关键参数的正交设计
2.1 关键参数的选取
2.2 正交试验设计
2.3 正交仿真试验结果
3 结果讨论与分析
4 结束语

