基于CEEMD-VMD-SIST算法的sEMG信号降噪方法

李 效，张 明，张 倩，叶 轩

(武汉纺织大学 电子与电气工程学院，武汉 430000)

0 引言

表面肌电(sEMG，surface electromyography)信号作为一种生物信号，包含了大量表征生物肌肉特征的信息，因此可以通过对其进行检测与处理进而实现手势识别、机械外骨骼控制等的研究与应用，例如通过对检测到的sEMG信号进行特征提取操作识别当前动作实现对机械外骨骼运动的控制。又因其能够超前肢体运动30～150 ms产生，且采集过程无创，如使用氯化银电极或MYO臂环即可实现sEMG信号的采集，而备受国内外研究人员关注。

然而，sEMG信号作为一种非线性非稳定信号，强度极其微弱[1]，其频率主要分布在10～500 Hz，通常在人体这个复杂环境中极易被淹没，而且在采集过程中也会不可避免地引入下面3种外界干扰：基线漂移(BW，baseline wandering)、工频干扰(PLI，power line interference)与高斯白噪声(GWN，Gaussian white noise)[2-3]。这其中基线漂移主要是由于电极、皮肤以及肌肉之间的相对位移导致的，其频率范围通常为1～10 Hz；工频干扰则来自环境中的电磁噪声，我国的工频干扰频率主要为50 Hz；高斯白噪声的频谱则分布于全频段，与sEMG信号频谱范围相交。若根据频带分布情况，这些干扰可分为非频率混叠与频率混叠两类，前者可以使用经典滤波器滤除，后者却很难做到。sEMG信号中噪声的存在会大大影响后续基于sEMG信号的手势识别准确率，因此有必要对含噪sEMG信号进行降噪处理。

目前对被高斯白噪声污染的sEMG信号进行降噪是一个研究热点，其目的主要是在尽可能地降噪的同时最大程度上保留sEMG信号中的有用信息。传统降噪算法主要有小波阈值降噪、小波包阈值降噪、经验模态分解(EMD，empirical mode decomposition)降噪等。其中小波阈值降噪因其简单有效而得到广泛应用，如孙志杰等人[4]在小波阈值降噪中通过调整小波基函数及其分解层数在布里渊光时域反射仪的降噪过程中取得了较好的降噪效果；王晨等人[5]在小波阈值降噪中通过调整小波母函数、分解层数、阈值规则和阈值函数的一系列参数在布里渊光时域反射仪的降噪过程中的降噪过程中取得了更好的降噪效果；马东等人[6]在小波阈值降噪中通过改进小波阈值及其小波阈值函数在sEMG信号的降噪过程中取得了很好的降噪效果。但因小波阈值降噪对高频系数的分解度不够以及频率混叠现象常常导致降噪效果不佳，而小波包阈值降噪虽然提高了分解度但仍然存在频率混叠现象以及小波母函数选择、阈值设置等诸多参数选择的困难。鉴于EMD具有自适应性和设置参数较少的特点，有学者将其与小波结合，如席旭刚等通过使用EMD对sEMG信号进行分解，利用自相关函数对其模态分量(IMF，intrinsic mode function)进行选择重构，使用小波降噪算法对重构后信号进行处理，取得了较好的降噪效果[7]；刘晓光等人[8]通过使用EMD对sEMG信号进行分解，利用样本熵对含噪IMF进行选择，使用小波降噪算法对选中的IMF进行处理，结果显示重构后的sEMG信号降噪效果较好；石志远等人[9]通过使用EMD对含噪信号进行分解，利用互相关函数对IMF进行选择，使用小波降噪算法对选中的IMF进行降噪处理，结果显示重构后的信号降噪效果更好。该类算法重点对选中的IMF进行小波阈值降噪，在提高分解度的同时，一定程度上也改善了降噪效果，但该方法并没有考虑两种分解算法本身的不足，在实际使用中该分解算法容易导致各模态分量之间的频率混叠，导致使用Donoho等提出阈值降噪效果不佳[10-11]。遂有学者使用互补集合经验模态分解(CEEMD，complementary ensemble empirical mode decomposition)与小波包的联合降噪算法，如董利超等人[12]使用CEEMD对含噪信号进行分解并利用自相关函数客观界定含噪IMF范围，利用小波包降噪算法对选中的IMF进行降噪处理，重构后的心音信号取得良好降噪效果。只是该方法未能考虑到小波包分解方法存在的频率混叠问题，而变分模态分解(VMD，variational mode decomposition)算法能够有效避免这样的问题，如吴田等人[13]在sEMG信号的降噪研究中直接使用VMD算法对信号进行分解，该方法切实有效地避免了各IMF之间频率混叠问题，取得了较好的降噪效果。

众所周知，GWN是随机且均匀分布的。如果能先用CEEMD方法对噪声信号进行预处理，初始中心频率更集中在低频处，有利于后续的VMD处理。为此，本文提出了一种基于CEEMD与VMD的sEMG信号滑动区间软阈值(SIST，sliding interval soft threshold)降噪算法(CEEMD-VMD-SIST)，该算法利用CEEMD对噪声信号进行预处理，初始中心频率更集中在低频处，有利于后续的VMD处理。首先，采用CEEMD方法对噪声信号进行自适应分解，得到一组本征模态函数(IMF)；接着，根据自相关系数客观地界定降噪信号的模态分量范围；然后，对选中的模态分量采用VMD进行分解，由于为有限频带以及分量间中心频率互斥从而避开了模态混叠问题，进而避免了因使用小波包而带来的模态混叠问题；最后使用SIST算法对含噪sEMG信号进行阈值降噪处理。实验结果表明，使用本文所提算法对含噪sEMG信号进行降噪处理，与传统降噪算法相比，其信噪比与均方根误差均有明显改善，可以更大程度上保留有用信息。

1 CEEMD-VMD-SIST降噪算法

1.1 CEEMD算法

CEEMD算法是以EMD为基础，在集合经验模态分解(EEMD，ensemble empirical mode decomposition)的基础上进行改进的一种算法，由于引入的是互补噪声，所以在重构信号时的冗余噪声会在很大程度上被消除，而无需进行上百次EMD，从而提高了计算效率[14-15]。CEEMD算法主要包括以下几个步骤：

1) 将n组正负成对的白噪声信号加入原始信号x(t)中，从而生成两组IMF集合：

(1)

式中，n(t)为辅助白噪声，其幅值可选x(t)标准差的0.2～0.5倍或可随噪声的强度而调整增大。m1、m2分别表示加入成对的正负白噪声后的信号。

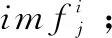
3) 对多组IMF进行求均值操作：

(2)

式中，imfj为x(t)经过CEEMD分解后的第j个IMF，能较好地保证信号的完整性，同时能很好地解决EMD的模态混叠现象，并能很大程度地解决集合经验模态分解导致的时间复杂度高的问题。将原始sEMG信号进行CEEMD分解前5层结果如图1所示，图中可以看出信号的各个频段分量被很好地分离，具有信号完整性。

图1 原始sEMG信号的CEEMD分解的前五层

1.2 VMD算法

VMD算法是首先构建一个变分模式分解模型，接下来不断地迭代求解各个模态分量，然后估计满足带宽之和最小时的最优解[16-17]，最后将输入信号f(t)自适应地分解成有限带宽的K个本征模态函数(BIMF，bandlimited intrinsic mode function)，该过程产生的约束变量模型如下：

(3)

式中，{uk}、{ωk}分别表示分解后的K个BIMF分量和相应的中心频率。∂t代表函数对时间t的偏导数。δ(t)为狄拉克分布(Dirac distribution)函数。

为了求解约束变分模型的最优解，引入惩罚因子α和Lagrange乘法算子λ，构建无约束的增广Lagrange函数，表达式如下：

(4)

采用交替方向的乘子算法(ADMM，alternate direction method of multipliers)来求取增广Lagrange函数中的“鞍点”[18]，这其中迭代更新(uk)，(ωk)和λ的更新公式如下：

(5)

(6)

(7)

式中，^ 表示傅里叶变换；τ表示噪声容忍参数；n表示迭代次数。

(8)

影响VMD算法性能的参数主要包括模态数M、惩罚因子α、噪声容忍参数τ和判别精度ε。如果模态数过少，会导致数据分割不足，出现模态混叠，而过多的模式数往往会导致额外噪声的产生。因此，模态数M的选择会对性能产生影响，针对本文sEMG降噪信号经过测试对比M取12为最佳，其它参数一般设置为：α为3 000，τ为0，ε为1e-7[19]。

1.3 基于CEEMD与VMD的sEMG滑动区间软阈值降噪

由上述CEEMD算法可知，经CEEMD分解后的原始含噪信号被分解为若干个IMF，其分解过程可看作是自适应滤波过程，即将含噪sEMG信号自适应地分解为一组从高频到低频的不同尺度的IMF。对于含噪sEMG信号，其经CEEMD分解后一般认为噪声多集中于低阶IMF，而有用信号的大部分能量多集中于高阶IMF，即低频段。因此，分量阶数越小，对应频率越高，集中的能量越少，必然会存在一个分界点b，使得imf1～imfb为噪声主导分量。

由于原始sEMG信号含噪水平不同，导致分界点b发生变化，即不存在一个普遍适用性的分界点b，因此，这边需要一种客观判定标准来确定分界点b。

为了能够客观确定这个分界点b，本文采用自相关系数进行确定。自相关函数定义为：

Rx(t1，t2)=E[x(t1)x(t2)]

(9)

随机信号的自相关系数反映了信号与自身在不同时间点时的相似程度，白噪声随机性的值在除零点外每个时间点之间是弱相关，图2表示强度为5 dBW的高斯白噪声及其自相关系数。而一般信号每个时间点的值之间都有一定的相关性，其特点是强相关。因此高斯白噪声主导的IMF自相关系数体现出白噪声特性，在零点处取极大值而其它点处约等于零；而有用信号主导的IMF的自相关系数是在零点处取极大值，但是其余时刻是向两侧震荡衰减至零，如图3所示。

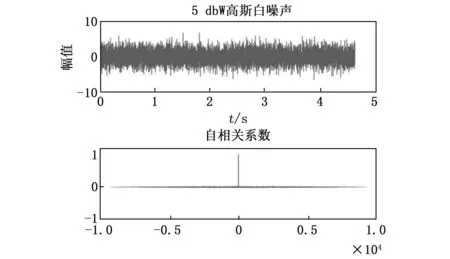
图2 5 dbW高斯白噪声及其自相关系数

为了能够准确表示噪声与有用信号的相关程度，本文采用归一化自相关函数[20]：

(10)

式中，Rx(0)和Rx(j)分别为延迟时间为零和j的自相关系数。采用CEEMD算法分解SNR=5 的某一sEMG信号得到的IMF自相关系数如图4所示，显然能够通过设定幅值阈值由自相关系数波形确定分界点b。

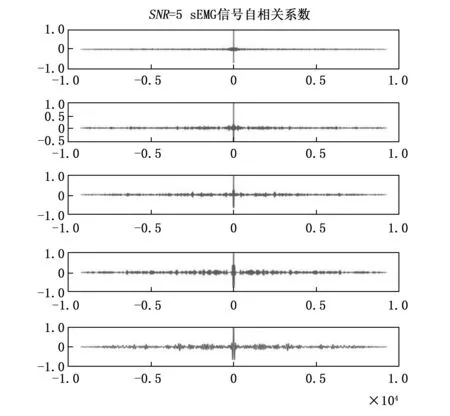
图4 sEMG信号自相关系数(SNR=5)

实际sEMG信号的能量主要集中在50～150 Hz，此外信号中含有很多尖峰和凸起，为了能够保存信号的更多细节，本文仅对imf1～imfb进行降噪处理，并将其与剩余未处理分量进行重构，即可得到降噪后信号。

本文所提算法流程如图5所示，其步骤如下：

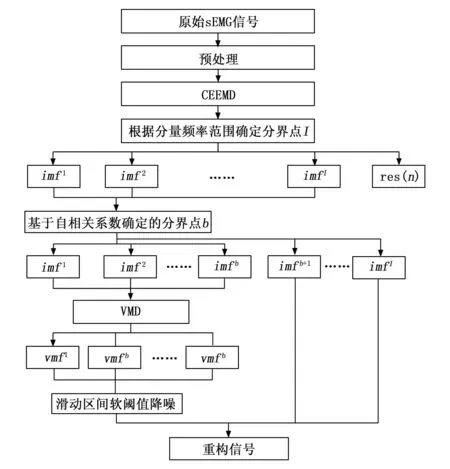
图5 本文所提算法流程图

首先，对原始含噪信号进行预处理，采用最大最小值归一化与零均值处理方法。

其次，对预处理后含噪信号进行CEEMD算法处理，经CEEMD分解得到的公式为：

(11)

式中，d(n)表示信号分解结果；imfi(n)表示CEEMD的第i个分量；I表示分解层数，由信号的频谱范围决定；这里res(n)表示分解后的残差。将频谱范围低于20 Hz的分量作为残差res(n)去掉以减小基线漂移的影响。

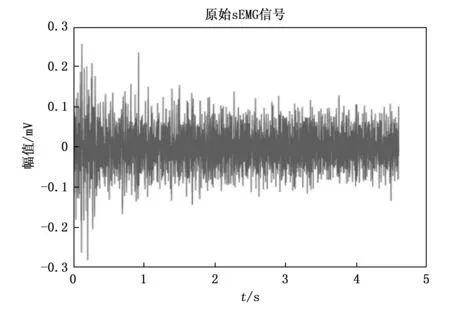
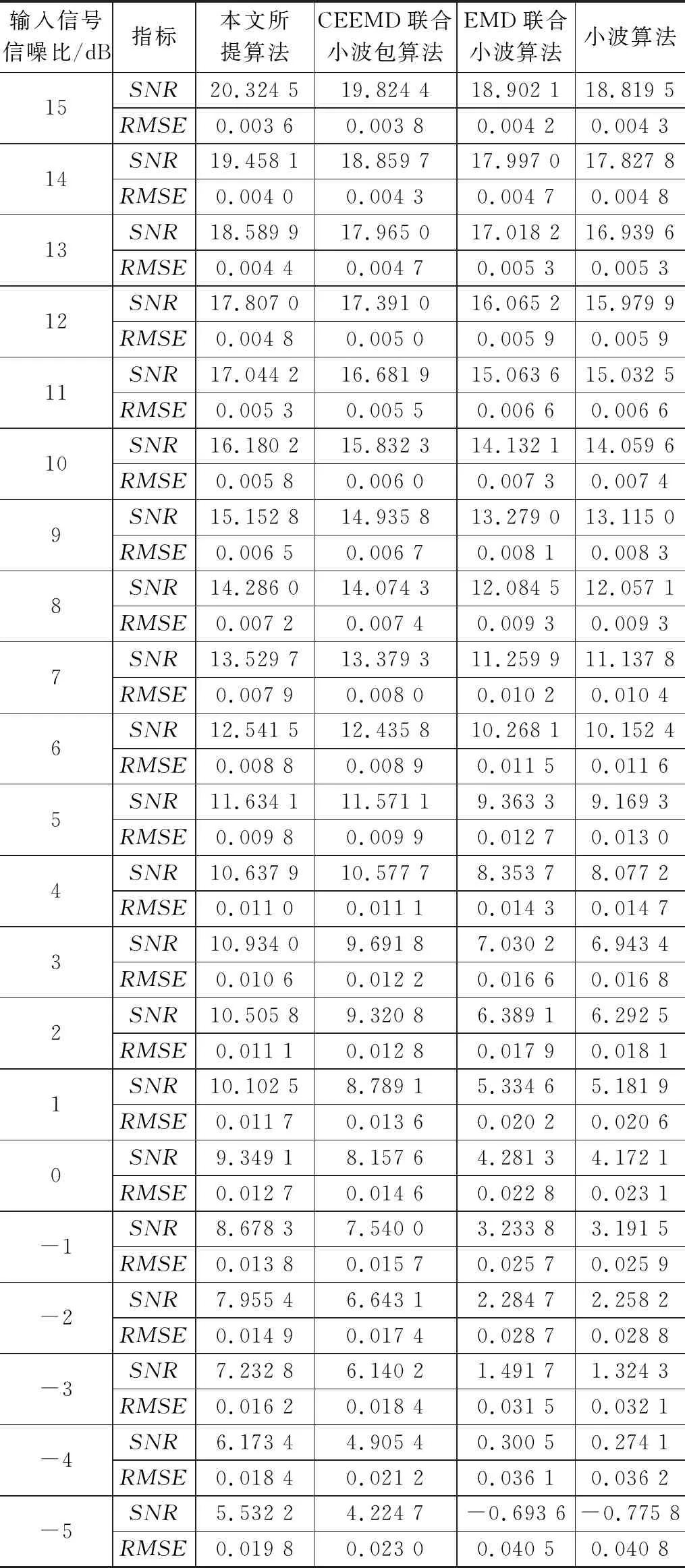
再次，根据自相关系数分析法对分量进行分类，得到白噪声主导的分量imf1～imfb(b

然后，采用滑动区间软阈值方法进行降噪其表达式如公式(12)所示：

(12)

(13)

式中，L为vmfi的长度，σi为vmfi的噪声方差，它的表达式为：

(14)

式中，vmfi为imfi进行VMD操作后的模态分量矩阵中的第j个分量。

最后，对vmf1～vmfb和imfb+1～imfI进行重构，得到降噪后的信号。

2 实验与分析

2.1 降噪效果评估指标

为了能够评估降噪性能，本文将采用信噪比(SNR，signal-to-noise ratio)与均方根误差(RMSE，root mean square error)两个指标进行评估各种算法的降噪效果，更大的SNR、更小的RMSE代表更佳的降噪性能。

(15)

(16)

式中，x(i)为原始sEMG信号，s(i) 为降噪后的sEMG信号，L为信号长度。

2.2 实验及分析

为了验证提出的降噪算法，本文搭建了sEMG信号的数据采集与手势识别系统，如图6所示，该系统的数据采集采集部分首先由前端采集电路使用差分放大方式对sEMG信号进行采集，采样频率为1 000 Hz，然后采用单片机通过蓝牙无线通信方式向上位机发送数据，最后上位机将接收到的原始数据保存为文本格式供后续处理。

图6 实验平台

同时为了更好地展示本文所提出的CEEMD-VMD-SIST算法的降噪性能，将与小波降噪、EMD联合小波降噪、CEEMD联合小波包降噪这3种算法进行降噪效果的对比测试。

实验将采用某一手指动作的sEMG信号，如图7所示，通过向图7所示的原始sEMG信号中分别叠加不同大小的高斯白噪声，以模拟不同信噪比的含噪sEMG信号。本文中，将参数I与b分别设置为8和5。

图7 原始sEMG信号

采用上述4种降噪算法分别对不同信噪比的信号进行降噪，降噪效果图分别如图8～10所示，其中图(a)为小波降噪算法处理结果，图(b)为EMD联合小波降噪算法处理结果，图(c)为CEEMD联合小波包降噪算法处理结果，图(d)为本文所提算法的降噪处理结果，图中的小图部分则表示信号的局部放大图。

图8 4种算法降噪性能比较(SNR=15)

图9 4种算法降噪性能比较(SNR=10)

图10 4种算法降噪性能比较(SNR=0)

2.3 降噪性能分析

在图8～10中，小波、EMD联合小波的降噪结果不是很理想，信号中大量的高频噪声未消除。从局部放大图展示的结果中可明显看出在同一噪声水平下，本文所提算法性能较好，且该优势随着噪声水平的提高而越发明显。CEEMD联合小波包降噪算法与本文所提算法的降噪效果接近，都能够有效地去除信号中的高频噪声，在信噪比较大时降噪结果基本一致，但随着信噪比的减小，两者略有差异，需进一步分析。

为了更加精确地比较各种降噪算法的降噪效果，本文使用SNR和RMSE两个指标来评价算法的降噪效果。采用同2.2节中的信号和算法，并取不同信噪比进行实验得到图11与表1所示。

表1 多种噪声水平下4种算法降噪效果

图11 多种信噪比下4种算法降噪效果

图11展示了不同信噪比下4种降噪算法的SNR和RMSE指标对比曲线，表1为图11中多种信噪比下4种算法降噪效果的SNR和RMSE具体指标的计算值。图11(a)中展示了使用4种降噪算法处理后，sEMG信号的SNR均可以得到不同程度的提升，这其中特别是本文所提算法的降噪效果最佳。图11(b)中则展示了使用4种降噪算法处理后的所取得的RMSE，其中本文所提算法所取得的RMSE值最小。

此外，从图11与表1中还可以看出，虽然CEEMD联合小波包算法的降噪结果与本文所提算法最为接近，但是随着噪声水平的提高可以明显看出本文所提算法所得SNR与RMSE两个指标均明显优于前者，即本文所提算法在强噪声条件下也能获得良好的降噪效果，自适应降噪能力更好。

3 结束语

为了改善对sEMG信号的降噪效果，本文提出了一种基于CEEMD-VMD-SIST降噪算法。通过使用原始sEMG信号进行实验，结果表明本文所提算法：

1) CEEMD与VMD组合克服了模态混叠的不足，同时也摆脱了小波类算法的参数选择困难问题。

2) 相比其它降噪算法，在不同噪声水平下特别是噪声水平较高的情况下能够取得更好的降噪效果。

因此，本文所提算法的降噪性能与其它3种降噪算法相比，信噪比与均方根误差这两个指标均有明显改善，且原始sEMG信号经其处理后，在后续手势识别中取得了更好的识别效果。