卫星导航多干扰源直接定位方法

任 洋，姚金杰，赵昶淳，邹 宇，薛晓东

(1.中北大学 信息探测与处理山西省重点实验室，太原 030051；2.内蒙航天动力机械测试所，呼和浩特 010076)

0 引言

随着我国卫星通信事业的蓬勃发展，卫星导航系统提供了准确的位置、导航和时间信息，给人们的生活带来便利。然而，卫星信号到达地面时信号强度微弱，受到干扰的情形逐年增多，这些干扰源可能会导致导航系统的服务中断或提供不准确的信息，造成一些问题。因此快速准确地定位干扰源，对于卫星导航系统的运行维护、用户的正常使用以及抗干扰能力的提升都至关重要[1-3]。

传统的卫星导航干扰源定位一般采用两步定位法，由估计中间参数和位置解算两个步骤组成[4]。首先，从接收机截获到的干扰信号中估计得到与干扰源位置相关的中间参数，如到达时间(TOA，time of arrival)、到达时间差(TDOA，time difference of arrival)、到达频差(FDOA，frequency difference of arrival)、到达角度(AOA，angle of arrival)等[5-7]；然后，基于中间定位参数，建立并求解关于目标位置的几何方程组，得到位置信息。从估计理论的角度来看，该方法是次优的，参数估计是在各接收基站独立进行，忽略了所有观测信号对应同一个目标这一客观约束[8]，且随着定位系统的传输、存储和计算能力的突飞猛进，两步定位法的低复杂度优势逐渐被淡化[9]。

直接定位 ( DPD，direct position determination )[10]方法充分利用了这一客观约束，联合所有信号构建依赖于干扰源位置的代价函数，再求得代价函数的最优解以获得目标位置[11-14]。但是对接收信号建模时，依然需要考虑干扰源位置信息蕴含在哪些变量即信息类型中，选取恰当的信息类型并建立准确的信号模型是保证直接定位精度的前提。直接定位的全局最优性是通过网格化参数空间并穷举搜索参数网格来实现的，为了得到高精度的定位结果，通常采用降低网格分辨率以增加网格密度的方法，但在穷举搜索时会导致计算复杂度呈指数增加。因此如何在降低计算复杂度的同时，提升定位精度是应用直接定位方法的关键所在。

在多干扰源定位场景中，Weiss等人[15]提出了基于多重信号分类(MUSIC，multiple signal classification)的多目标直接定位算法，在发射波形未知的情况下对样本自相关矩阵进行子空间分解，利用噪声子空间与信号子空间的正交性，构建代价函数，并通过谱峰检测估计各辐射源位置，但是必须知道目标辐射源的数量，且通常需要大量的快拍。在多干扰定位场景中目标提取是一个关键步骤，若无法成功提取目标，目标位置也难以确定，相应地，后续定位精度也会受到阻碍。因此Yi等人[16]在MUSIC定位方法的基础上给出了一种目标提取及位置估计的方法，通过消除已定位目标的影响，通过依次进行门限处理，按照目标强度依次定位出监测区域的目标，直至满足一定停止准则。针对该方法操作复杂这一问题，陈芳香等人[17]首先利用Akaike信息准则 (AIC，akaike information criterion) 来确定目标估计数，对于目标提取采用图像膨胀 (IE，image expansion) 算法，能够获得局部极大值点对应的位置坐标，但可能出现更多的误检测对象和不必要的噪声。在文献[18]中通过计算每个时刻的接收信号协方差矩阵，对协方差矩阵分块，计算得到传播算子，进而得到导向矢量正交投影子空间的估计，其定位精确度与传统MUSIC直接定位算法相当。Tirer 等人[8，19]根据最小方差无失真响应(MVDR，minimum variance distortion less response) 滤波准则，提出了基于 MVDR 的多目标直接定位算法，采用DPD结合MVDR算法的超分辨能力，可以得到多个目标的位置信息，但忽略了目标提取仍然采用穷举搜索法，导致计算复杂度较大这一问题。

针对上述问题，本文面向北斗导航接收机受到多个静态压制式干扰的定位场景，提出一种改进DPD_MVDR的直接定位方法，无需估计干扰源个数，对接收信号进行频域处理，构建代价函数，在目标提取这一关键技术上使用自适应网格细化方法，设置动态网格分辨率，降低计算复杂度的同时提高定位精度，通过仿真验证可达到所提方法的要求。

1 卫星导航多干扰源定位问题

1.1 系统与信号模型

假设如图1所示的北斗卫星导航静态多干扰源定位场景，存在G个干扰源，发射不同频率的压制式干扰信号，其干扰源位置的笛卡尔坐标为pg=(xg，yg)，g=1，2，...，G，设置系统空间中存在L个静止的接收机且彼此之间时频同步，每个接收机均配备有M个阵元构成的阵列天线，接收机的笛卡尔坐标用pl=(xl，yl)，l=1，2，...，L表示。如此搭建系统模型，使得关于干扰源的位置信息包含在了到达时间与到达角度中。

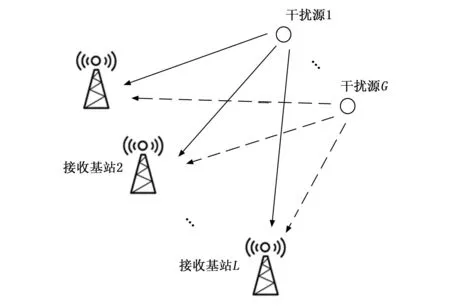
图1 静态多干扰源定位场景

假设信号参数对各接收机未知，每个接收机均能在视线范围内收到所有干扰源信号，则第l个接收机的接收信号可表示为：

0≤t≤T

(1)

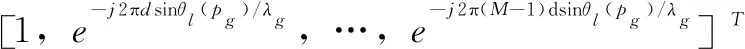
(2)

(3)

c是光速，arctan函数的范围[-π/2，π/2]，角度是与法线的夹角。从上述信号模型来看，干扰源位置信息包含在阵列响应al(θl(pg))与时延τl(pg)中，分别与干扰源到接收机之间的到达角度和到达时间有关，因此本文基于这两种信息类型来确定干扰源的位置。

1.2 自适应网格细化原理

传统直接定位算法采用的是固定网格分辨率，代价函数往往是非凸的，容易陷入局部最优解，且在目标提取时往往采取穷举搜索方法，该方法的计算复杂度与网格分辨率密切相关，网格分辨率同时决定了最终的目标定位精度，因此三者之间难以同时兼顾定位精度与计算复杂度即定位的实时性。网格精细化处理是常用来解决定位精度的方法[21-22]，通过增大网格密度提高定位精度，但往往带来巨大的计算量，也无法做到二者同时兼顾。本文在目标提取上采用自适应网格细化方法，首先，对感兴趣的区域以较高分辨率划分粗网格，遍历所有网格集合得到初始代价函数平面以及初始谱峰，该步骤为粗搜索；然后，分别在初始谱峰附近运用自适应网格细化并进行谱峰精细搜索，直到满足收敛条件则停止。使用该方法可以在得到较高定位精度的同时大幅度降低计算复杂度。

2 改进多目标直接定位算法

2.1 基于MVDR的直接定位算法

将式(1)中获得的接收信号rl(t)的观测时间T等分成K个时间片段，每段长度为I=T/K，且满足T/K≥max{τl(pg)}，即远大于干扰源到接收机的最大时延。对于任一感兴趣的干扰源目标信号，对第k个片段的接收信号进行傅里叶变换表示为：

rl(ωi，k)=αlal(θl(p))s(ωi，k)e-jωi[τl(p)+t0]+zl(ωi，k)，

k=1，…，K

(4)

其中：rl(ωi，k)与s(ωi，k)分别表示接收信号rl(t)与发射信号sg(t)在第k个时间片段的傅里叶变换谱，对应的频点数为I，zl(ωi，k)包含噪声和其他干扰源信号的干扰。

联合所有接收机接收信号定义下列向量和矩阵，并将含有干扰源位置信息的向量组合：

s(ωi，k) ≜s(ωi，k)e-j ωi t0

α≜[α1，…，αL]T

z(ωi，k) ≜[z1(ωi，k)，…，zL(ωi，k)]T

(5)

则第k个时间片段的第i个频点的所有接收机上的接收信号通过整理上式可以表示为如下向量形式：

(6)

联合K个时间片段可以得到第i个频点的LM×LM维的接收信号的协方差矩阵：

(7)

整理所有频点定义如下向量：

(8)

根据MVDR的基本原理，对接收信号空域滤波后，感兴趣的目标信号能够无失真地通过滤波器，从而得到基于MVDR的目标估计函数：

(9)

其中：

(10)

wopt(p，α)表示空域滤波器的权向量，最小化了除p即目标之外所有源的总输出能量，因此它有望产生高分辨率且满足：

(11)

将式(11)的权向量代入式(9)中得到：

(12)

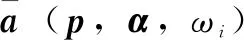
Β≜IL⊗lM

(13)

式中，IL表示L×L维的单位矩阵，lM表示M×1维的全1矩阵，⊗表示克罗尼克乘积，则得到的Β是一个LM×L的矩阵。

将式(13)代入式(12)得到目标估计函数：

(14)

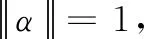
(15)

λmax(·)表示求矩阵的最大特征值，其中矩阵ZL×L是包含有干扰源位置信息的数据矩阵。最终，得到基于MVDR的目标代价函数：

(16)

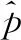
2.2 自适应网格细化估计位置

(17)

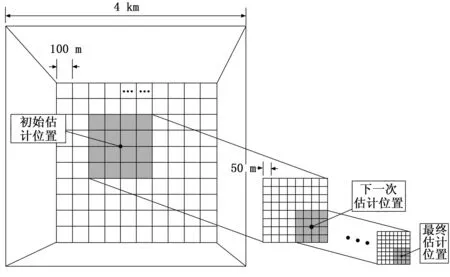
图2 迭代网格细化

根据上式i的设定决定了每次迭代过程中选择覆盖的范围，当i=1时则表明，每次迭代范围为估计位置所在的一倍分辨率。

由于在每一次迭代中，上一次的估计值都包含在下一次网格区域中，所以第k次的解是第k+1次的可行解，这确保了目标的最优值不会随迭代的进行而增加。直到第k次迭代的定位结果与k-1次结果相差小于1 m时，停止迭代，选择第k次的结果为最终的干扰源位置。

2.3 改进的DPD_MVDR算法流程

基于 MVDR 算法与自适应网格细化算法相结合的改进多干扰源直接定位算法，其具体实现流程如下：

1)确定干扰源所在位置的二维搜索区域，将搜索区域栅格离散化处理后的位置坐标集合作 为搜索空间Ωx_grid×y_grid[23]；

2)在频域上对接收信号rl(t)作傅里叶变换，将接收信号分成K个部分，每个部分包含有I个频点，对于每个部分根据式(4)计算其在单个频点上的rl(ωi，k)，并按式(5)得到r(ωi，k)；

5)对于每个网格点，根据式(2)计算其时延τl(pi)；在每个网格点下遍历I个频点，在每个频点处根据式(13)计算得到Λωi(p)与矩阵Β，然后根据式(15)将I个频点求和得到单一网格位置处的矩阵Z；

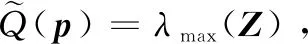
7)所有网格点重复5)与6)得到最终的代价函数平面；

8)根据代价函数平面的函数值由大到小得到干扰源数目的局部极大值点，并得到极大值点对应的位置坐标，构成初始位置估计值；

9)将自适应网格细化算法应用于估计位置所在的小区域内，进行迭代细化，得到最终的估计值。其整体算法操作流程如图3所示。

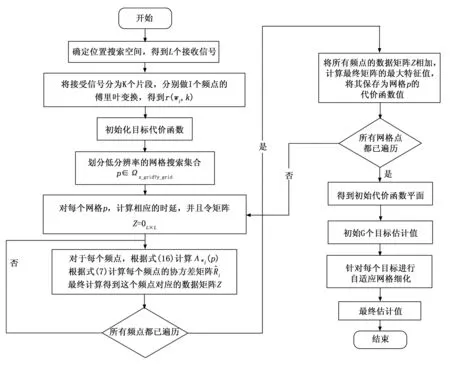
图3 算法流程图

3 实验结果与分析

为了验证算法的性能，采用目标有效提取率(EER，effective estimate rate)和目标均方根误差(RMSE，root mean square error )两个评价指标：

(18)

式中，N为蒙特卡洛仿真次数；Ne为所有实验中目标位置估计结果出现在有效范围内的实验次数；xj，yj为第j次实验得到的目标位置估计值。有效提取率越高，定位算法越有效，计算估计位置的RMSE才具有统计参考意义。

3.1 算法定位性能验证

仿真场景如图4所示：初始定位区域为4 000 m×4 000 m，设置有5台接收机(即L=5)，每个接收机都配置有由7个阵元(即M=7)组成的均匀线阵，阵元间距取为半波长；存在3个静止的压制式干扰源，分别发射针对北斗B1C、B2a与B2b的单音干扰，避免产生相干信号对实验结果造成影响。

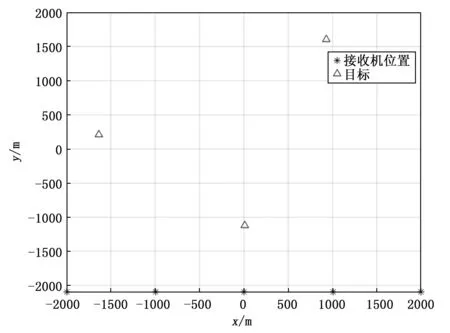
图4 定位场景图

设置干扰源的坐标分别为 (-1 635，210；10，-1 120；930，1 605) m，接收机的坐标分别为(-2 000，-2 100；-1 000，-2 100；0，-2 100；1 000，-2 100；2 000，-2 100 )m。通道衰减的建模公式为αl=1+δl，其中δl是一个圆形的、复的高斯随机变量，均值为0标准差为 0.1，每个接收机和干扰源的信道衰减独立绘制。使用本文所提算法，定位结果基于5个频点的2 000个快拍，当设置信噪比为10 dB，初始网格分辨率为100 m，自适应网格细化覆盖范围i=2时，定位结果如图5所示。其中在三维定位结果图中干扰源所在位置有明显的峰值，定位误差均小于1 m；在代价函数平面图中，颜色越亮的区域表示该区域的代价函数值越大，分别对应 3个干扰源位置，验证了算法具有较高的定位精度。

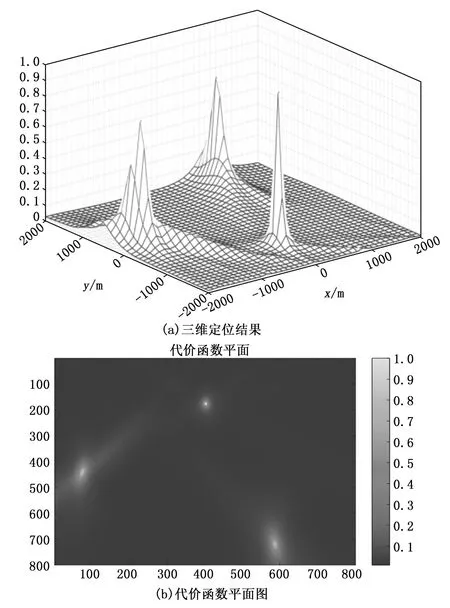
图5 定位结果图

为了进一步验证所提算法的定位精度，设置在100 m的网格分辨率下，分别与DPD_MVDR、DPD_MUSIC以及DPD_MUSIC+自适应网格细化3种算法进行对比，设置如上所示的仿真条件，分别在信噪比为-20：5：20 dB环境下蒙特卡洛300 次，检验算法的定位精度。图6分别给出了4种算法针对3个干扰源定位结果的EER和RMSE随信噪比变化的曲线图，为便于直观比较算法的定位性能，分别将它们对同一目标的性能曲线绘制在了同一幅图片中，其中将出现在真实目标位置 500 m范围内的定位结果认定为有效定位。

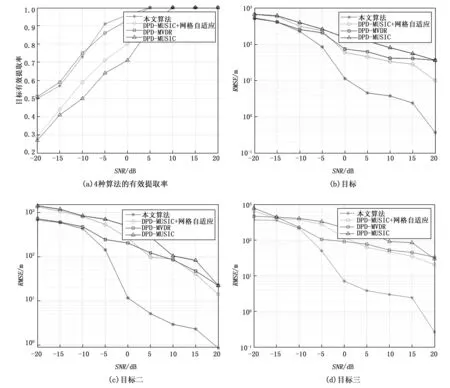
图6 4种算法的EER与RMSE

从图6(a)中可以看出4种方法的目标有效提取率均随着信噪比的增大而增大并最终收敛于1，在低信噪比情况下，4种算法的有效提取率都比较低，主要因为噪声干扰导致代价函数峰值位置出现偏差，位置捕获错误；在中信噪比情况下，本文算法的有效提取率明显高于其他3种方法，对比发现加有网格自适应的改进DPD_MUSIC算法其有效提取率也高于没有添加这一优化的DPD_MUSIC算法，主要因为添加有网格自适应的算法可以不断迭代，重新划分更细的网格搜索集合，降低定位误差提高提取率，由此证明了加有自适应网格细化方法的多目标直接定位算法可以提高定位精度。

图6(b)、(c)、(d)分别表述了3个干扰源使用4种算法的目标估计RMSE随信噪比变化情况，3张图中随信噪比的增大4种算法的RMSE均呈下降趋势。从图6(b)中可以看出，在低信噪比条件下4种算法由于目标有效提取率较低造成误差均很大；随着信噪比的增大，对于DPD_MVDR与DPD_MUSIC算法由于实验设置的网格分辨率为100 m，因此误差范围至少在100 m及以上导致定位精度较差；对比增加有网格自适应的DPD_MUSIC算法以及本文算法，其定位精度随着信噪比的增大而逐渐提高，因为其在初始估计值处逐渐增大网格分辨率，提高了定位精度，验证了所提算法可以改进DPD_MVDR直接定位算法的定位精度。

3.2 算法计算复杂度验证分析

在上一小节中验证了在网格分辨率为100 m的情况下，改进算法能够有效提高干扰源的定位精度，由于计算复杂度与网格分辨率密切相关，网格分辨率同时决定了最终的目标定位精度。因此设置网格分辨率为5 m，对于DPD_MVDR直接定位算法其定位精度小于5 m，但计算复杂度远远高于100 m下的所提算法的计算复杂度，验证了传统的DPD_MVDR直接定位算法无法做到二者的同时兼顾。

本文所提的多干扰源定位方法其计算量是k次迭代的网格细化过程中使用DPD_MVDR方法的计算量之和。为了验证所提算法能够做到定位精度与计算复杂度二者同时兼得，在DPD_MVDR定位算法中，为了得到较高精度的定位结果，需要提高网格分辨率，设置在定位区域为4 000 m×4 000 m的范围内网格分辨率为5 m，则计算量为8012个网格点下，分别在I个频点下计算数据矩阵Z并对其进行特征值分解，寻找最大特征值，其计算复杂度为O(8012(I(2(ML)2+L3+L)))；设置本文所提算法的网格分辨率为100 m，进行k次迭代的计算复杂度为O((412+3k(4i+1)2)(I(2(ML)2+L3+L)))，理论上计算复杂度优于单独使用DPD_MVDR算法。表1展示了上述两种情况下以及网格分辨率为100 m的情况下DPD_MVDR单独一次实验所用的时间，可以看出所提算法所用时间大大低于传统方法，且与100 m分辨率下的传统算法耗时差不多，但定位精度却大大提高，验证了所提算法在得到较高定位精度的同时降低了计算复杂度。

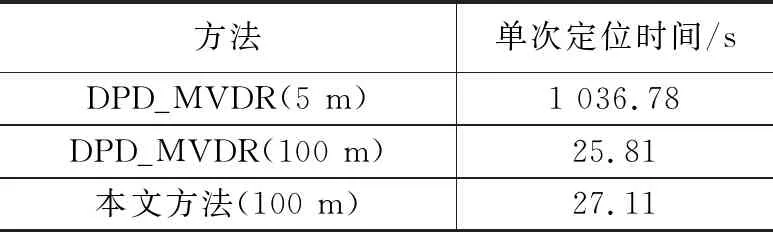
表1 不同方法单次定位时间

3.3 相关参数对定位性能的影响

在上述仿真中，接收机上均配备有7阵元的均匀线阵，由于使用均匀线阵进行直接定位，最多可定位的干扰源个数为M-1个，在本次仿真中共有3个干扰源，因此阵元数不能低于4。考虑到目标提取率在0 dB后逐渐收敛于1，为了更直观验证阵元数目对定位性能的影响，设置信噪比为0 dB。其他参数与上述仿真相同，阵元个数分别为 5：2：13时，蒙特卡洛独立仿真300次，绘制3个干扰源的RMSE随阵元数变化曲线如图7所示，所提算法的定位性能随着阵元数的增大而逐渐提高，这是由于阵元数越多意味着接收到的信号能量越多，在信号处理后获得的信噪比增益越大，由此算法的定位精度会越高，但阵元数增多导致成本增加，因此本文中选用阵元数为7。

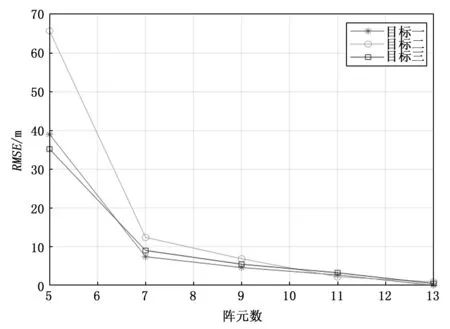
图7 RMSE随阵元数变化曲线

所提算法在最终进行自适应网格细化迭代时，网格区域的迭代覆盖范围受参数i的设定，通过仿真分析i分别取1，2，3情况下其中一个干扰源定位精度随信噪比变化情况如图8所示。在低信噪比条件下，由于目标有效提取率较低，3种情况下的误差均很大；随着i值的增大，定位精度也逐渐提高；在高信噪比下，i=3时会由于覆盖范围太大，涉及了别的目标源，导致误差增大。因此在仿真场景中选用i=2的情况，相比大范围的区域划分，在带来较小精度损失的情况下降低了计算复杂度。

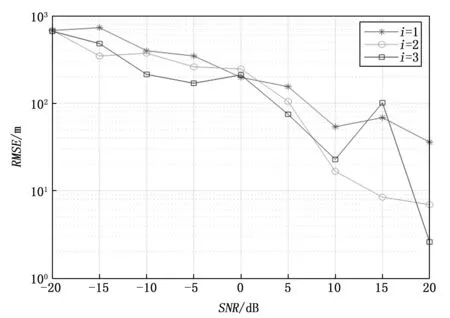
图8 参数i不同时的RMSE曲线

4 结束语

本文面向卫星导航多干扰源定位场景，使用自适应网格细化方法改进传统的DPD_MVDR直接定位算法，无需已知或估计干扰源的数量，只在初始估计值处进行网格细化，证明在100 m的网格分辨率下，本文算法定位精度高于DPD_MVDR算法，与5 m网格分辨率下的DPD_MVDR相比，100 m下的本文算法在得到同样高定位精度的同时降低了计算复杂度，做到了能够很好地兼顾定位精度与计算复杂度，适用于对定位精度和定位实时性均有较高要求的场景。为了得到更高精度的定位结果，可以结合神经网络训练多干扰源位置，以训练结果为中心缩小搜索范围，之后再结合自适应网格细化，由此可以大幅度提高目标有效提取率得到更高的定位精度。现有的研究成果对于卫星导航系统存在多个静止的干扰源并对其进行及时准确地定位有着重要意义，对于多个同频干扰源造成的相干信号的直接定位也是本文后续的主要研究内容。