考虑温度应力动态变化的继电保护装置可靠性研究

龚杰，徐习东，杨剑友，方愉冬

（1.浙江大学 电气工程学院，杭州 310027；2.国网浙江省电力有限公司温州供电公司，浙江 温州 325000；3.国网浙江省电力有限公司，杭州 310007）

0 引言

继电保护是保证电网安全稳定运行的第一道防线，继电保护装置的寿命评估、检修退役决策直接影响到了电网的安全稳定运行［1-2］。为了避免提前退役装置造成不必要的经济浪费或延迟退役装置带来的安全隐患，对继电保护装置的可靠性进行合理的评估是十分必要的。

继电保护装置在可靠性模型上为各部件组成的串联系统，任何部件的失效都会导致保护装置的失效。文献［3］推导了考虑数据检修、截尾特性的基于极大似然估计的继电保护装置恒定失效率计算方法和最小二乘拟合方法，但是其没有考虑装置老化的情况。文献［4］采用基于对数正态分布的寿命模型，并使用最小二乘法和平均秩次法进行参数估计。文献［5-6］采用三参数威布尔分布函数对继电保护装置失效率数据进行拟合，得出三参数Weibull 模型中各参数的数值。文献［7］以部件为基本单位，假设部件服从威布尔分布，给出串联、并联以及表决系统寿命与剩余寿命数值计算方法；文献［8］提出了一种基于三参数威布尔分布的灰色估计法，提高了在小样本情况下其可靠性参数估计精度和速度。但是以上文献的模型中没有体现出环境应力对保护装置可靠性的影响。若计及保护装置的失效率与环境、运维水平、制造工艺等多重因素，保护装置的失效率有更多的不确定性。文献［9］提出利用长期影响因素修正系数和短期影响因素修正系数来描述长短期影响因素对装置失效率的影响，但是其修正系数的量化较为困难。

继电保护装置内部包含大量的电子元器件。这些元器件在运行过程中，不可避免地受到各种环境应力的影响，如温度变化、湿度波动、机械振动等。评估应力对装置寿命的影响，可以采用各种应力加速模型，常见的应力加速模型有：Arrhenius 模型［10］、逆幂律模型［11］、艾琳模型［12］、Peck模型［13］、Relia模型［14］。

温度是影响继电保护装置寿命和可靠性最重要的环境因素［5］。针对温度应力的复杂动态变化，本文将保护装置运行环境温度视为一个服从正态分布的随机变量，结合Arrhenius［10］与Weibull分布模型，建立基于温度应力动态变化的保护装置可靠性模型，通过上述模型采用数值分析的方法，分析了保护装置的失效概率密度、可靠度和失效率随温度应力特征参数变化的特点。

1 基于威布尔分布的失效模型

Weibull 模型因其能灵活地模拟浴盆曲线［15］的各个阶段而在可靠性分析中得到广泛应用［16］。Weibull分布的失效分布函数F(t)、失效概率密度函数f(t)、可靠度函数R(t)和失效率函数λ(t)如式（1）—（4）所示：

式中：t为运行时间；β为形状参数；η为尺度参数。其中当β<1时，失效率随时间的推移而减小，对应浴盆曲线的早期失效阶段；当β=1 时，失效率不随时间而改变，对应浴盆曲线的偶然失效阶段；当β>1 时，失效率随时间的推移而增大，对应浴盆曲线的耗损失效阶段。Weibull 模型中各项参数通常根据统计的失效数据计算得出。

大量的文献采用Weibull函数描述保护装置的寿命分布，并且Weibull分布的形状参数在失效机理不变时为一个定值，而尺度参数则与受到的应力水平有关［17-21］。应力对寿命特征的影响，可以用应力加速模型来表征。因此，一些文献用加速寿命模型表征尺度参数［22］。

2 考虑温度应力动态变化的继电保护装置可靠性模型

2.1 温度应力对老化失效率的影响

Arrhenius 在1880 年提出了Arrhenius 模型［10］被广泛应用在描述温度应力对装置寿命的影响，其表达式为：

式中：ζ为特征寿命，如中位寿命等；A为常数且A>0，可以通过大量试验数据利用参数估计方法［5］求得；E为激活能，主要与产品的材料有关，在失效机理不变情况下，可认为是常数，一般通过加速寿命试验或加速退化试验得出；K为波尔兹常数，K=8.617×10-5eV；T为绝对温度，约等于摄氏温度加273.15。

若寿命分布服从Weibull分布的保护装置工作在恒定温度Ti下，则Weibull函数中的尺度参数可用式（6）表示：

将式（6）代入式（2）—（4），可求得恒定温度Ti下，继电保护装置的失效概率密度函数、可靠度函数和失效率函数，如式（7）—（9）所示：

2.2 温度的变化特征

虽然有文献认为继电保护装置的内部温度总是随运行年限而升高［22］，温度T可以用一个随运行时间递增的函数表达，但是考虑到开关柜中保护装置的运行温度不仅会随季节的变化而上下波动，同一季节内也会呈现一定的随机波动，因此，用一个单调函数来表征温度变化有一定的局限性。以某地区2019—2021年的环境日均温度数据为例，并考虑保护装置内部一定的温升，可以得到保护装置的温度数据如图1所示。

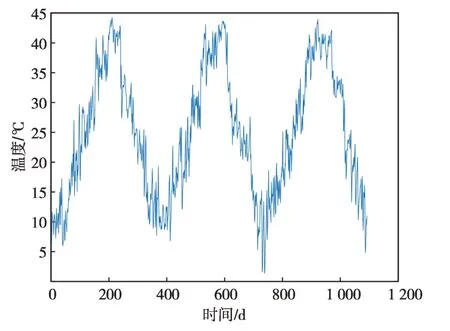
图1 2019—2021年日均温度变化曲线Fig.1 Daily temperature change curve from 2019 to 2021

对于图1所示的温度变化，难以用一个时间函数表达。因此我们把温度变化描述为一个正态分布的随机变量，温度分布的概率密度函数如式（10）所示：

式中：μT为装置运行期间温度的均值；σT为装置运行期间温度的方差。

考虑式（5）中温度T为绝对温度，因此把图1中的温度转换成绝对温度；然后利用极大似然估计法计算，可以得出该地区的保护装置内部温度的均值μT为298.21 K，标准差σT为10.69。

2.3 基于温度应力动态变化的保护装置可靠性模型

当温度T为一个正态分布的随机变量，其概率密度函数如式（10）所示，由条件概率密度函数以及温度应力分布的概率密度函数可以推导得到保护装置失效的全概率密度函数、可靠度函数和失效率函数。概率密度函数、可靠度函数和失效率函数分别如式（11）—（13）所示：

式（11）—（13）与式（7）—（9）相比，增加了两个环境温度参数，即温度的均值和温度的方差。显然不同温度均值和方差会影响失效率和可靠度的变化特征。

以某型号的继电保护装置为例，装置的活化能E采用国际通用的经验值0.7 eV。本文利用文献［23］中在恒定应力下得到的失效数据，采用最小二乘法估计得到A和β分别为1.206 5×10-8和3.384 1。根据2.2节计算得出温度的均值μT和准差σT，利用数值计算的方法并忽略温度T变化至5σT以外的情况，根据式（12）—（13）可计算得出装置运行在该地区开关柜内的可靠度期望值曲线和失效率期望值曲线，分别如图2和图3所示。

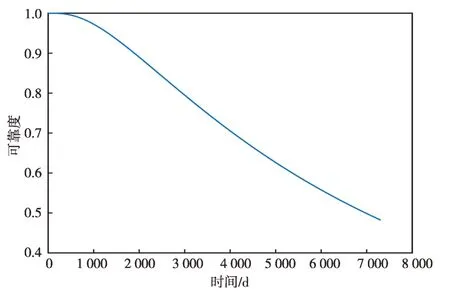
图2 装置的可靠度期望值曲线Fig.2 Curve of expected device reliability

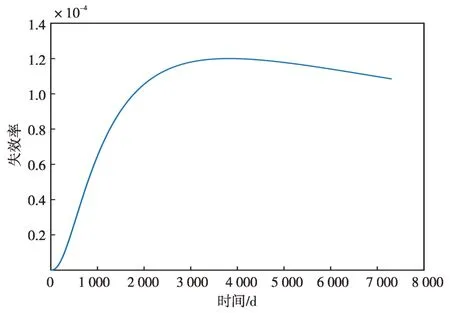
图3 装置的失效率期望值曲线Fig.3 Curve of expected failure rate of device

图2说明装置运行期间，其可靠度是不断下降的，该地区此型号保护装置的可靠度不低于80%的工作年限为6.8年。由图3可知，装置的失效率刚开始快速增长，一定时间后失效率出现缓慢下降的情况，这是由于在复杂的温度应力条件下，尺度参数处于动态变化之中造成的结果。如果所有同类型的装置在其失效率最高或之前强制退役，则很难观测到后期失效率下降的情况。

3 温度特征参数变化对保护装置可靠性的影响分析

3.1 温度均值对装置可靠性的影响分析

不同地区其环境温度是存在差别的，为分析温度均值对保护装置可靠性的影响，分别选取绝对温度的均值为295.15 K（22 ℃）、299.15 K（26 ℃）、303.14 K（30 ℃）三种情况进行对比；除此之外，考虑温度的波动，分别针对方差为7、9、11、13四种情况下对f（t）、R（t）、λ（t）进行分析计算。数值计算结果如图4—6所示。

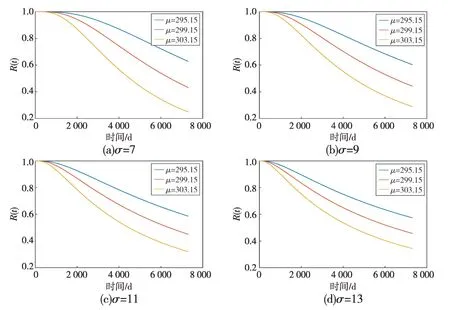
图4 不同μ下f（t）的对比情况Fig.4 Comparison of f（t）at different μ values

图4表明：在相同方差下，温度的均值越大其失效概率密度函数f（t）的最大值出现的时间越早，其最大值也越大。

图5表明：在相同方差和时间的情况下，温度的均值越高，其可靠度越低。从图5也显示，可靠度衰减不是线性的，在前期，温度均值越高其可靠度衰减得越快，一定临界时间后，温度均值越高其可靠度衰减得越慢。

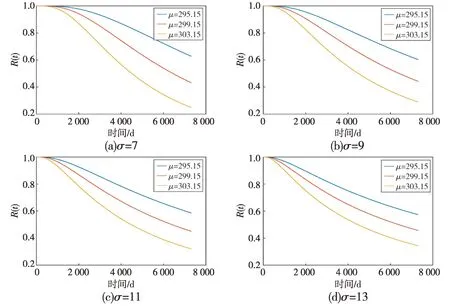
图5 不同μ下R（t）的变化情况Fig.5 Variation of R（t）at different μ values

图6表明：在方差一定的情况下，温度均值越高，失效率越高，与图4、图5的结论一致。虽然从图5中可以看到可靠度是持续减小的，但是失效率在一定年限以后是会逐渐降低的，这是复杂温度应力下，Weibull尺度参数发生动态变化的结果。

图6 不同μ下λ（t）的变化情况Fig.6 Variation of λ（t）at different μ values

3.2 温度方差对装置可靠性的影响分析

为探讨温度动态变化幅度对装置可靠性的影响，在同一温度均值下，对比方差不同时概率度、可靠度和失效率曲线的变化情况分别如图7—9所示。

图7 不同σ下f（t）的对比情况Fig.7 Comparison of f（t）at different σ values

图7表明：在相同的温度均值的情况下，方差越大其概率密度函数f（t）的最大值出现的时间越早。但方差对概率密度函数f（t）最大值的影响有限，也不是线性关系。

图8表明：在温度均值相同的情况下，在一定时间内，方差越小，可靠度越高；超出某个临界时间后，方差越小，可靠度越低。对比图8中三个分图可以发现，温度均值越大临界时间点出现得越早。

图8 不同σ下R（t）的变化情况Fig.8 Variation of R（t）at different σ values

图9表明：在相同的温度均值的情况下，在一定时间内，方差越大，失效率随时间增加的速度越快；在一定临界时间后，方差越大，失效率随时间增加的速度越慢，甚至当方差大于一定值时，失效率会出现下降的情况；与图8的可靠度结论一致。图9 中三个分图进一步显示了温度均值越大，临界时间出现的越早。

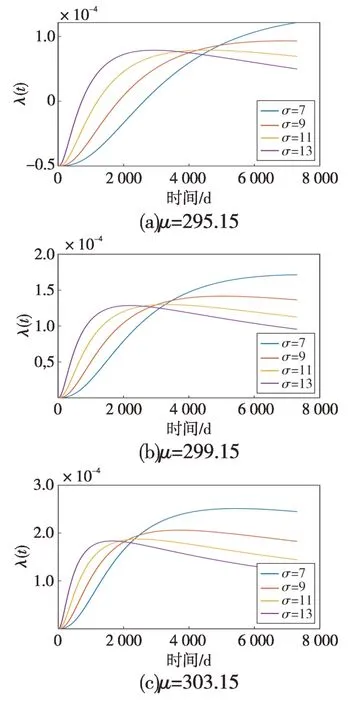
图9 不同σ下λ（t）的变化情况Fig.9 Variation of λ（t）at different σ values

上述数值分析结果表明当Weibull函数中的尺度参数在动态温度应力下发生动态变化时，Weibull 函数的形状在某个临界点后会发生改变，因此采用Weibull函数对长期在复杂应力环境下使用的装置统计分析时，应充分注意这种形状的改变。

4 结论

考虑保护装置运行环境动态变化，本文提出了一组基于温度应力动态变化的继电保护装置的可靠性模型。基于该模型，选取不同温度均值及方差对失效概率密度、可靠度和失效率分别进行数值计算分析，得到动态温度应力下保护装置可靠性的一些特征如下：

1）温度的均值越大其概率密度函数的最大值越大，出现的时间越早，即温度越高，早期失效越多。若考虑温度动态变化，动态变化越大，即温度方差越大，失效概率密度函数的最大值出现的时间越早。即温度动态变化范围越大，即使温度均值较低，早期失效情况也会增多。

2）温度的均值越高，其可靠度随时间衰减越快。在同一温度均值下，若考虑温度动态变化，则存在一个临界时间点，在临界时间点之前，温度方差越小，可靠度越高；超出这个临界时间点后，温度方差越大，可靠度越高。温度方差对可靠度非线性衰减的过程有较大影响。

3）若运行时间相同，则温度均值越高，失效率越高，这与传统的温度越高，老化失效越快是一致的。若考虑温度动态变化，动态变化越大，失效率在一定临界时间以后是会逐渐降低，这是复杂温度应力下，Weibull 尺度参数会发生动态变化的结果。且温度均值越大，临界时间出现的越早。