具有无症状感染的新冠病毒传播模型研究

原玉茹 李淑萍

摘  要：为研究无症状感染者对新冠病毒的传播影响，建立了一个具有无症状感染的新冠病毒传播动力学模型.首先，利用下一代矩阵法求得基本再生数R0.其次，当R0＜1时，应用Hurwitz判据证明了无病平衡点的局部稳定性，并通过构造Lyapunov函数的方法证明了无病平衡点的全局稳定性；当R0＞1时，系统存在唯一的地方病平衡点且是局部渐近稳定的，并证明了系统的一致持续性.然后，利用最优控制理论，求得了最优控制解的表达形式.最后，通过数值模拟验证了理论结果，并对参数进行敏感性分析，说明无症状感染者对新冠病毒传播的影响程度不容忽视，应采取居家隔离措施来降低疾病的传播率.

关键词：无症状感染；稳定性；一致持续；最优控制；敏感性分析

中图分类号：O175.1      文献标志码：A文章编号：1000-2367（2024）03-0071-09

传染病是人类生存的最大威胁之一，传染病的反复流行，不仅影响人类的身体健康，更大程度上损害了社会利益，因此流行病学和其他生物学领域的研究人员开始了解传染病并尝试通过模型的研究来揭示疾病的流行规律，预测流行趋势，为发现、预防和控制疾病的流行提供理论根据和策略.从2019年末起，由严重急性呼吸综合征冠状病毒2（severe acute respiratory syndrome coronavirus 2，SARS-CoV-2）引起的新型冠状病毒感染在中国和世界各地蔓延.该病毒的症状表现为干咳、发烧和疲劳，进一步还可能导致肺炎、肾衰竭甚至死亡［1-4］.这种病毒可以通过身体接触、打喷嚏和咳嗽时的飞沫在人与人之间传播，并且越来越多的证据表明，新冠病毒的快速传播在一定程度上是由无症状感染者驱动的.

无症状感染者是一类具有传染性但是没有相关临床症状的群体，他们隐藏在人群中不容易被发现，因此在病毒的传播过程中，这类群体会发挥很大的作用.无症状感染者的出现频率和传染性是新冠病毒大流行的主要原因，在一项研究中，将流行病学数据与估计数据的44%的无症状感染者比例进行了比较，发现无症状感染的个体比输入病例更容易引起更大的疫情［5］.为了更加深入地了解新冠病毒的快速传播与无症状感染者之间的关系，一大批的专家学者建立了相关的传染病模型.DOBROVOLNY［6］建立了一个包含无症状感染的仓室数学模型，预测到在感染高峰期会有更多的无症状或未报告的病例.该研究显示，即使无症状感染不一定占感染的很大比例，它仍可以改变流行病的规模和致命性.但该模型有一点不足的是，尚未考虑疾病的潜伏期，这就可能导致同一个仓室内包含有不同感染率的人，这种个体的混合对参数估计的准确性会有很大影响.GU等［7］建立了一类包括住院、隔离和检疫的SEIAQHR模型，通过详细的数值模拟结果强调了社交距离、隔离和检疫等干预措施的必要性.SUN等［8］基于一个来自黑龙江省的数据驱动模型SCIRA模型来估计无症状患者的影响，结果表明由于无症状患者也具有传染性，這些隐蔽病例的潜在影响应引起广泛关注.

收稿日期：2022-12-29;修回日期：2023-09-22.

基金项目：国家自然科学基金（11701528）.

作者简介：原玉茹（1997-），女，山西晋城人，中北大学硕士研究生，研究方向为生物数学，E-mail：yuanyrjy@126.com.

通信作者：李淑萍，E-mail：lspnuc@126.com.

引用本文：原玉茹，李淑萍.具有无症状感染的新冠病毒传播模型研究［J］.河南师范大学学报（自然科学版），2024，52（3）：71-79.（Yuan Yuru，Li Shuping.A study of a COVID-19 transmission model with asymptomatic infection［J］.Journal of Henan Normal University（Natural Science Edition），2024，52（3）：71-79.DOI：10.16366/j.cnki.1000-2367.2022.12.29.0001.）

上述各种研究表明，无症状感染者这些隐藏病例，对于传染病建模而言无疑是不可忽略的.

在本文中，建立了一个包含无症状感染的病毒流行的仓室模型，并进行动力学分析，以确定无症状个体在新冠病毒传播中发挥的作用.

1  模型的建立

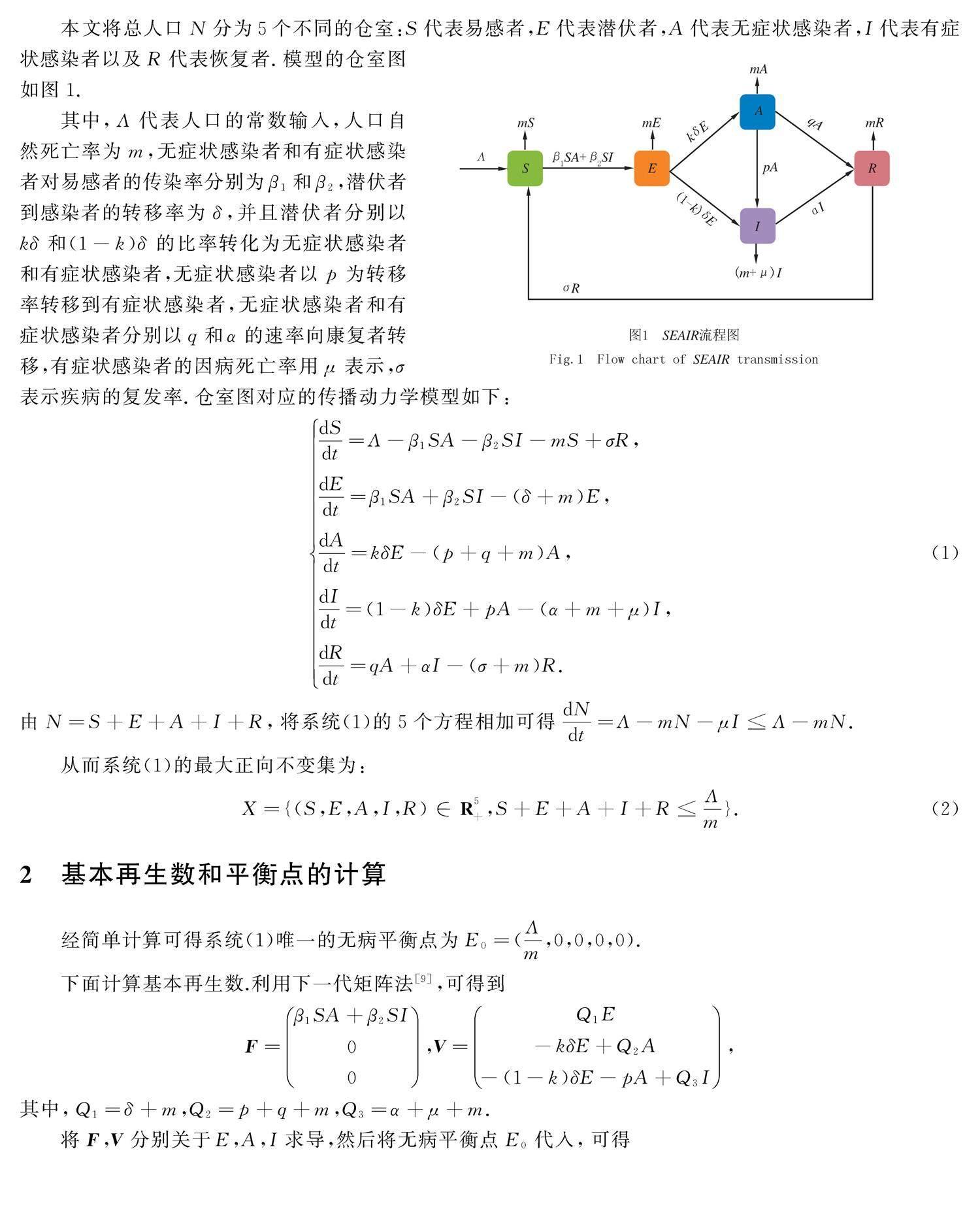
本文将总人口N分为5个不同的仓室：S代表易感者，E代表潜伏者，A代表无症状感染者，I代表有症状感染者以及R代表恢复者.模型的仓室图如图1.

其中，Λ代表人口的常数输入，人口自然死亡率为m，无症状感染者和有症状感染者对易感者的传染率分别为β1和β2，潜伏者到感染者的转移率为δ，并且潜伏者分别以kδ和（1-k）δ的比率转化为无症状感染者和有症状感染者，无症状感染者以p为转移率转移到有症状感染者，无症状感染者和有症状感染者分别以q和α的速率向康复者转移，有症状感染者的因病死亡率用μ表示，σ表示疾病的复发率.仓室图对应的传播动力学模型如下：

dSdt=Λ-β1SA-β2SI-mS+σR，dEdt=β1SA+β2SI-（δ+m）E，dAdt=kδE-（p+q+m）A，dIdt=（1-k）δE+pA-（α+m+μ）I，dRdt=qA+αI-（σ+m）R.（1）

由N=S+E+A+I+R，将系统（1）的5个方程相加可得dNdt=Λ-mN-μIΛ-mN.

从而系统（1）的最大正向不变集为：X=｛（S，E，A，I，R）∈R5+，S+E+A+I+RΛm｝.（2）

2  基本再生数和平衡点的计算

经简单计算可得系统（1）唯一的无病平衡点为E0=（Λm，0，0，0，0）.

下面计算基本再生数.利用下一代矩阵法［9］，可得到

F=β1SA+β2SI00，V=Q1E-kδE+Q2A-（1-k）δE-pA+Q3I，

其中，Q1=δ+m，Q2=p+q+m，Q3=α+μ+m.

将F，V分别关于E，A，I求导，然后将无病平衡点E0代入，可得

F=0β1Λmβ2Λm000000，V=Q100-kδQ20-（1-k）δ-pQ3.

从而有FV-1=kδβ1ΛmQ1Q2+（1-k）δβ2ΛmQ1Q3+kδpβ2ΛmQ1Q2Q3β1ΛQ3+pβ2ΛmQ2Q3β2ΛmQ3000000.

因此，基本再生数为R0=r1+r2+r3，（3）

其中，r1=kδβ1ΛmQ1Q2，r2=（1-k）δβ2ΛmQ1Q3，r3=kδpβ2ΛmQ1Q2Q3.

将系统（1）的地方病平衡点记为E*=（S1，E1，A1，I1，R1）.为求解地方病平衡点，令模型（1）右端为0，即Λ-β1S1A1-β2S1I1-mS1+σR1=0，β1S1A1+β2S1I1-（δ+m）E1=0，kδE1-（p+q+m）A1=0，（1-k）δE1+pA1-（α+m+μ）I1=0，qA1+αI1-（σ+m）R1=0.（4）

可解得S1=Q1Q2Q3kδβ1Q3+（1-k）δβ2Q2+kδpβ2，E1=Q2kδA1，

A1=R0-1R0kδQ3（σ+μ）Q1Q2Q3（σ+μ）-σkδqQ3-σα（1-k）δQ2-σαkδp，

I1=（1-k）Q2+kpkQ3A1，R1=kqQ3+α（1-k）Q2+αkpk（σ+m）Q3A1.

经计算，S1，E1，A1，I1，R1均为正.因此，当R0＞1时，系统（1）存在唯一的地方病平衡点E*=（S1，E1，A1，I1，R1）.

3  平衡点的稳定性

3.1  无病平衡点的稳定性

定理1  當R0＜1时，系统（1）的无病平衡点E0在X内是局部渐近稳定的；当R0＞1时，无病平衡点不稳定.

证明  系统（1）在E0处的Jacobian矩阵为J|E0=-m0-β1Λm-β2Λmσ0-Q1-β1Λm-β2Λm00kδ-Q2000（1-k）δp-Q3000qα-（σ+m）.

矩阵J|E0的特征方程为（λ+m）（λ+σ+m）（λ3+b1λ2+b2λ+b3）=0.（5）

显然，已有λ1=-m，λ2=-（σ+m）为方程（5）的两个负实根，并且b1=Q1+Q2+Q3＞0，b2=Q1Q2（1-R1）+Q1Q3（1-R2）+Q2Q3＞0，b3=Q1Q2Q3（1-R0）＞0.

进一步得：b1b2-b3=Q1（Q1+Q2+Q3）（Q2（1-R1）+Q3（1-R2））+Q2Q3（Q2+Q3）+Q1Q2Q3R0＞0.

因此，由Hurwitz判据［10］可知，当R0＜1时，系统（1）在无病平衡点E0处局部渐近稳定.当R0＞1时，b3＜0，此时无病平衡点不稳定.

定理2  当R0＜1时，系统（1）的无病平衡点E0在X内是全局渐近稳定的.

证明  构造Lyapunov函数V=（kδQ1Q2β1+kδp+（1-k）δQ2Q1Q2Q3β2）E+（β1Q2+pβ2Q2Q3）A+β2Q3I＞0.

当R0＜1时，dVdt=（kδQ1Q2β1+kδp+（1-k）δQ2Q1Q2Q3β2）E′+（β1Q2+pβ2Q2Q3）A′+β2Q3I′=

（kδQ1Q2β1+kδp+（1-k）δQ2Q1Q2Q3β2）（β1SA+β2SI-（δ+m）E）+（β1Q2+

pβ2Q2Q3）（kδE-（p+q+m）A）+β2Q3（（1-k）δE+pA-（α+m+μ）I）=

（R0-1）（β1A+β2I）0.

令Ω=｛（S，E，A，I，R）|dVdt=0｝=｛（S，E，A，I，R）|A=I=0｝，在Ω内，当t→∞时，有S→Λm，因此｛E0｝是Ω的最大ω不变集.从而由LaSalle不变集原理可知，X内的任何轨线都趋于E0，无病平衡点E0在X内全局渐近稳定.

3.2  地方病平衡点的稳定性

定理3  当R0＞1时，若满足c（ab-c）＞a2e及（ae-f）（abc-c2-a2e）＞f（ab-c）2+af2，那么系统（1）的地方病平衡点E*在X内是局部渐近稳定的.其中，a=a11+a12+m+a13，b=a14-a15+a11（a12+m+a13）+（a12+m）a13，

c=a11a13（a12+m）+（a14-a15）（a12+m+a13）+a12a15，

e=a13（a12+m）（a14-a15）+a12（a16+a13a15-σα（1-k）δ-σkδq），f=a12（a13a16-ασpkδ-ασ（1-k）δQ2-σqkδQ3）.

且有a11=Q1+Q2+Q3，a12=β1A1+β2I1，a13=σ+m，

a14=Q1Q2+Q1Q3+Q2Q3，a15=（1-k）δβ2S1+kδβ1S1，a16=Q1Q2Q3.

证明  系统（1）在E*处的Jacobian矩阵为J|E*=-β1A1-β2I1-m0-β1S1-β2S1σβ1A1+β2I1-Q1β1S1β2S100kδ-Q2000（1-k）δp-Q3000qα-（σ+m）.

J|E*的特征方程为λ5+aλ4+bλ3+cλ2+eλ+f=0.（6）

经计算可得，a，b，c，e，f＞0.当R0＞1时，若满足以下条件［11］：

（i）c（ab-c）＞a2e;（ii）（ae-f）（abc-c2-a2e）＞f（ab-c）2+af2.

那么矩阵J|E*的5个特征值均有负实部.通过Hurwitz判据可知，系统（1）的地方病平衡点E*在X内是局部渐近稳定的.

4  系统的持续性

定理3  当R0＞1时，系统（1）是一致持续的，即存在一个正数ε，使得limt→∞ inf（A（t），I（t），R（t））（ε，ε，ε）.

证明  首先由集合X见式（2），定义集合X0=｛（S，E，A，I，R）∈X|E，A，I，R＞0｝，X0=X＼X0.

由系统（1）第2个方程可得：E（t）E（t0）e-（σ+m）（t-t0）＞0，（7）

由系统（1）第3个方程可得：A（t）A（t0）e-（p+q+m）（t-t0）＞0，（8）

由系统（1）第4个方程可得：I（t）I（t0）e-（α+μ+m）（t-t0）＞0，（9）

由系统（1）第5个方程可得：R（t）R（t0）e-（σ+m）（t-t0）＞0.（10）

因此X和X0是正不变集，X0是X的相对闭集.接下来证明系统（1）是一致持续的.记M=｛（S（0），E（0），A（0），I（0），R（0））|（S（t），E（t），A（t），I（t），R（t））∈X0，t0｝.

现在证明M=｛（S（0），0，0，0，0）|S（t）0｝显然已有｛（S（0），0，0，0，0）|S（t）0｝M下面只需要证M｛（S（0），0，0，0，0）|S（t）0｝.

设（S（0），E（0），A（0），I（0），R（0））∈M则需证明对t0，有E（t）=0，A（t）=0，I（t）=0，R（t）= 0.利用反证法，假设结论不成立，则存在t00，使得下式之一成立：

（i）A（t0）＞0;（ii）I（t0）＞0;（iii）R（t0）＞0;（iv）E（t0）＞0.

对于情况（i），对式（8）形式求解可得对所有t＞t0，有A（t）＞0.进一步由系统（1）可得E（t）＞0，I（t）＞0，R（t）＞0.因而有（S（t），E（t），A（t），I（t），R（t））X0，产生矛盾.对于情况（ii）和情况（iii），由同样的方法也可得出与（S（0），E（0），A（0），I（0），R（0））∈M矛盾.而对于第（iv）种情况，即E（t0）＞0，当t＞t0时，可得A（t）=A（t0）e-（p+q+m）（t-t0）+∫tt0kδEe（p+q+m）tdt，显然E（t0）＞0时，对于t＞t0，有A（t）＞0.同理可求得I（t）和R（t）的形式解，当t＞t0时有I（t）＞0，R（t）＞0.因此（S（t），E（t），A（t），I（t），R（t））X0，得出矛盾.从而证得M=｛（S（0），0，0，0，0）|S（0）0｝.系统（1）的无病平衡点E0全局渐近稳定，在M中只有一个平衡点E0.

下面将证明E0相对于集合X0是弱排斥的，即证limt→∞  sup d（Φ（t），E0）＞0，仅需证明Ws（E0）∩X0=即可.利用反证法，假设此结论不成立，则系统（1）存在一个正解（S（t），E（t），A（t），I（t），R（t）），使得limt→∞（S（t），E（t），A（t），I（t），R（t））=（S0，0，0，0，0）.

定义M=F-V，因为R0＞1，所以s（M）＞0.对于足够小的ε＞0，有s（M-Mε）＞0.其中，

Mε=0β1εβ2ε000000.

存在T＞0，使得对任意的t＞T，有S0-ε＜S（t）＜S0+ε.

从而可得如下微分方程不等式dEdtβ1（S0-ε）A+β2（S0-ε）I-（δ+m）E，

dAdt=kδE-（p+q+m）A，dIdt=（1-k）δE+pA-（α+m+μ）I.

考虑辅助系统dEdt=β1（S0-ε）A+β2（S0-ε）I-（δ+m）E，

dAdt=kδE-（p+q+m）A，dIdt=（1-k）δE+pA-（α+m+μ）I.（11）

因为s（M-Mε）＞0，所以当t→∞时，E（t）→∞，A（t）→∞，I（t）→∞，這与假设t→∞时，E（t）→0，A（t）→0，I（t）→0相矛盾［12］，从而证得Ws（E0）∩X0=.综上所述，可得系统（1）关于（X0，X0）是一致持续的.

5  最优控制理论

由于传染病的建模一般都涉及大量的参数，因此研究具有最佳控制干预措施的疾病动态就显得很有必要，为了使模型能够比较精准地预测现实，最优控制理论常被用来提出最有效的策略以便减少人们的疾病负担.以下针对新冠病毒的传播，提出并研究了4种控制策略，目标是在疫情防控期间尽量减少受感染人数和相应策略的成本.

定义U=｛ui|i=1，2，3，4｝其中u1表示减少易感者与无症状感染者接触的隔离策略，u2表示减少易感者与有症状感染者接触的隔离策略，u3表示提高无症状感染者的治疗恢复率的控制策略，u4表示提高有症状感染者的治疗恢复率的控制策略.将与时间相关的控制纳入系统（1）中，用以确定控制疾病的最优策略，可得到非线性微分方程组如下：dSdt=Λ-β1（1-u1）SA-β2（1-u2）SI-mS+σR，

dEdt=β1（1-u1）SA+β2（1-u2）SI-（δ+m）E，

dAdt=kδE-（p+q+m+u3）A，dIdt=（1-k）δE+pA-（α+m+μ+u4）I，dRdt=qA+αI+u3A+u4I-（σ+m）R.（12）

目标函数是J（u1，u2，u3，u4）=∫T0（P1A+P2I+ω12u21+ω22u22+ω32u23+ω42u24）dt，其中P1和P2分别表示无症状感染者和有症状感染者的权重系数;ω1，ω2，ω3，ω4分别代表各个控制策略对应的权重系数;ω12u21，ω22u22，ω32u23，ω42u24分别表示对应的控制策略所需的成本.

控制集U=｛（u1（t），u2（t），u3（t），u4（t））|0ui（t）1，i=1，2，3，4｝，且ui（t）在［0，1］上是勒贝格可测的.

定义Y=（S，E，A，I，R）则目标集χ可表示为χ=｛Y（·）∈W1，1（［0，T］;R5）|Y（·）满足式（1）和（12）｝.

存在u*=（u*1，u*2，u*3，u*4），使得J=（u*1，u*2，u*3，u*4）=minu1，u2，u3，u4∈UJ（u1，u2，u3，u4）.（13）

根據Pontryagin Maximum原理［13］，对于最终时间T上固定的问题（13），若U（·）∈χ为最优解，则存在一个非平凡的绝对连续映射λ∶［0，T］→R5，且λ（t）=（λ1（t），λ2（t），λ3（t），λ4（t），λ5（t）），称为伴随变量，有

（1）控制系统满足dSdt=Hλ1，dEdt=Hλ2，dAdt=Hλ3，dIdt=Hλ4，dRdt=Hλ5.

（2）伴随系统满足dλ1dt=-HS，dλ2dt=-HE，dλ3dt=-HA，dλ4dt=-HI，dλ5dt=-HR.

（3）极小值条件H（Y*（t），U*（t），λ*（t））=min0＜ui＜uimaxH（Y*（t），U（t），λ*（t））.

对于t∈［0，T］成立，将哈密顿函数H定义为H（Y，U，λ）=P1A+P2I+ω12u21+ω22u22+ω32u23ω42u24+λ1［Λ-β1（1-u1）SA-

β2（1-u2）SI-mS+σR］+λ2［β1（1-u1）SA+β2（1-u2）SI-（δ+m）E］+

λ3［kδE-（p+q+m+u3）A］+λ4［（1-k）δE+pA-（α+m+

μ+u4）I］+λ5［qA+αI+u3A+u4I-（σ+m）R］，（14）

此外，有横截条件λi（T）=0，i=1，2，…，5成立.

定理4  存在最优控制U（t）以及最优解（S*（t），E*（t），A*（t），I*（t），R*（t））满足最终时间T固定的最优控制问题（13），且存在伴随函数λ*i（·），（i=1，2，…，5），使得dλ*1dt=［β1（1-u1）A+β2（1-u2）I］（λ*1-λ*2）+mλ*1，

dλ*2dt=（δ+m）λ*2-kδλ*3-（1-k）δλ*4，

dλ*3dt=-P1+β1（1-u1）S（λ*1-λ*2）+（p+q+m+u3）λ*3-pλ*4-（q+u3）λ*5，

dλ*4dt=-P2+β2（1-u2）S（λ*1-λ*2）+（α+m+μ+u4）λ*4-（α+u4）λ*5，

dλ*5dt=-σλ*1+（σ+m）λ*5，

且有横截条件λ*i（T）=0，i=1，2，…，5.

更进一步得到最优控制解被表示为如下形式：u*1（t）=min｛max｛0，（λ*2-λ*1）β1S*A*ω1｝，1｝，u*2（t）=min｛max｛0，（λ*2-λ*1）β2S*I*ω2｝，1｝，

u*3（t）=min｛max｛0，（λ*3-λ*5）A*ω3｝，1｝，u*4（t）=min｛max｛0，（λ*4-λ*5）I*ω4｝，1｝.

6  数值模拟

6.1  平衡点的稳定性

假设Λ=100，β1=0.000 1，β2=0.000 1，m=0.07，δ=0.4，σ=0.03，k=0.6，p=0.3，q=0.6，α=0.3，μ=0.05，可得R0=0.31＜1，如图2（a）所示，验证了无病平衡点是全局渐近稳定的.假设β1=0.001，β2=0.001 4，δ=0.7，σ=0.05，q=0.485，μ=0.066，可得R0=3.87＞1，如图2（b）所示，地方病平衡点是全局渐近稳定的.

6.2  敏感性分析

敏感性分析用于描述输入参数对输出变量的影响程度，其主要方法之一的偏秩相关系数法（PRCC）是一种非常有用的统计抽样技术，现已广泛应用于分析传染病模型领域［14］.本文通过利用拉丁超立方抽样法，对影响系统（1）的基本再生数R0的各个参数进行了敏感性分析，进而对这些参数影响R0的程度有了一定的判断.通过分析发现，在选取的参数中，m与R0呈显著负相关，Λ，β1，β2，k与R0呈显著正相关.从图3中可以发现，在这些对疾病的暴发有着不同程度影响的参数中，无症状感染者对易感者的传染率β1对R0的影响极大，因此可以通过降低β1来达到减少和控制传染病传播的目的；也可以通过增大无症状和有症状感染者的恢复率系数q和α来缩短传染病的治愈周期；或者通过减小人口的常数输入Λ来降低人口流动性，进而降低疾病的传播速度.

6.3  最优控制

在图4（b，c）中，得到了采取最优控制策略前后无症状感染者和有症状感染者的数量对比，很明显由于采取了控制策略，感染人数迅速趋近于0.这说明所研究的控制策略对于控制传染病的传播能够起到很好的作用，证明了控制策略的有效性.

7  结  论

本文建立了具有无症状感染的SEAIR模型，针对无症状感染者在新冠肺炎传播中的影响进行了研究.首先计算了模型的基本再生数，其次利用理论方法证明了无病平衡点的稳定性，并证明了系统的一致持续性.然后应用庞特里亚金极大值原理对一个最优控制问题进行了求解.最后通过数值模拟验证了理论结果的可靠性，并对参数进行敏感性分析，说明无症状感染者对疾病的传播影响不容忽视.隔离和社交距离是阻止感染传播的主要武器，因此国家可以重点从这方面入手，通过采取适当的措施，实行完善的隔离政策，提升人们对病毒的防范意识，减少易感人群与染病者之间的接触，最终达到控制疾病传播的目的.

参  考  文  献

［1］   KARIA R，GUPTA I，KHANDAIT H，et al.COVID-19 and its modes of transmission［J］.SN Comprehensive Clinical Medicine，2020，2（10）：1798-1801.

［2］LI X P，WANG Y，KHAN M A，et al.A dynamical study of SARS-COV-2：a study of third wave［J］.Results in Physics，2021，29：104705.

［3］KUMARI P，SINGH H P，SINGH S.SEIAQRDT model for the spread of novel coronavirus（COVID-19）：a case study in India［J］.Applied Intelligence，2021，51（5）：2818-2837.

［4］KANG X X，HU Y，LIU Z Y，et al.Forecast and evaluation of asymptomatic COVID-19 patients spreading in China［J］.Results in Physics，2022，34：105195.

［5］SUN T Z，WENG D.Estimating the effects of asymptomatic and imported patients on COVID-19 epidemic using mathematical modeling［J］.Journal of Medical Virology，2020，92（10）：1995-2003.

［6］DOBROVOLNY H M.Modeling the role of asymptomatics in infection spread with application to SARS-CoV-2［J］.PLoS One，2020，15（8）：e0236976.

［7］GU Y，ULLAH S，KHAN M A，et al.Mathematical modeling and stability analysis of the COVID-19 with quarantine and isolation［J］.Results in Physics，2022，34：105284.

［8］SUN T Z，WANG Y.Modeling COVID-19 epidemic in Heilongjiang Province，China［J］.Chaos，Solitons & Fractals，2020，138：109949.

［9］VAN DEN DRIESSCHE P，WATMOUGH J.Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission［J］.Mathematical Biosciences，2002，180（1/2）：29-48.

［10］馬知恩，周义仓，王稳地，等.传染病动力学的数学建模与研究［M］.北京：科学出版社，2004.

［11］LASALLE J P.动力系统的稳定性［M］.成都：四川科学技术出版社，2002.

［12］ZHANG F，ZHAO X Q.A periodic epidemic model in a patchy environment［J］.Journal of Mathematical Analysis and Applications，2007，325（1）：496-516.

［13］LI K Z，ZHU G H，MA Z J，et al.Dynamic stability of an SIQS epidemic network and its optimal control［J］.Communications in Nonlinear Science and Numerical Simulation，2019，66：84-95.

［14］李淑萍，苗慧.数据驱动下带环境病毒的新冠肺炎传播模型［J］.山西大学学报（自然科学版），2023，46（1）：131-140.

A study of a COVID-19 transmission model with asymptomatic infection

Yuan Yuru， Li Shuping

（School of Mathematics， North University of China， Taiyuan 030051， China）

Abstract： In order to study the influence of asymptomatic infection on the transmission of novel coronavirus， a transmission dynamics model of COVID-19 with asymptomatic infection is established. First， the basic reproduction number is obtained by the next generation matrix method. Secondly， when R0＜1， Hurwitz criterion is applied to prove the local stability of the disease-free equilibrium， and the global stability of the disease-free equilibrium is proved by constructing a lyapunov function; and when R0＞1， there is a unique endemic equilibrium and the system is locally asymptotically stable， proving the uniform persistence of the system. Then， using the optimal control theory， the expression form of the optimal control solution is solved. Finally， the theoretical results are verified by numerical simulation， and the sensitivity analysis of the parameters showed that the influence of asymptomatic infection on the transmission of novel coronavirus can not be ignored， and compulsory isolation measures should be taken to reduce the transmission rate of the disease.

Keywords： asymptomatic infection; stability; uniformly persistent; optimal control; sensitivity analysis

［责任编校  陈留院  赵晓华］