构建有效提问 优化数学课堂

嵇珍妮

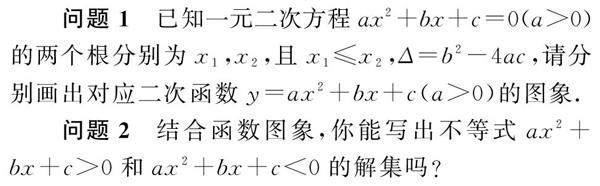
摘要：课堂提问在课堂教学中是必不可少的，它是激发学生学习热情，提升学生思维品质，提高教学效率的重要路径.有效提问可以引发学生思考，帮助学生主动获得知识，激发学生潜能，实现思维、能力的全面提升.本文中分析了课堂提问中存在的一些问题，并提出了几点有效策略，通过课堂提问的优化，促进学生综合能力和综合素养的全面提升.

关键词：课堂提问；有效提问；策略

课堂提问是一门教学艺术，是一种重要的教学手段，是师生双边活动的纽带.在高中数学教学过程中，要认真研究教学内容和学生，基于教学实际创设有效问题，指引学生向着成功的方向发展，促使学生积极思考，从而不断提升学生解决数学问题的能力，为提高课堂教学效果打下基础[1].下面笔者结合教学实践谈谈高职数学课堂提问现状，并结合教学实例提出创设有效问题的途径，以期通过有效问题的创设，让学生获得更高层次的发展.

1 高职数学课堂提问现状分析

在新课程背景下，大多教师会采用提问的方式提高学生参与课堂的积极性和主动性，以此充分发挥学生的主体作用，提高课堂教学实效.不过当前课堂提问还存在一定的弊端，主要有以下几个方面的问题.

1.1 提问数量过多

当下，“自主、合作、探究”教学模式成为数学课堂教学的主流.教学中，为了给学生创造更多的探究机会，有的教师一味地追求提问的数量，因而忽视了学生的自主学习意识，压缩了学生独立思考的时间和空间，这样的课堂表面上看热热闹闹，但是没有摆脱教师思维的束缚，影响学生发现、分析和解决问题能力的提升.

1.2 思考时间过短

数学课堂教学往往时间紧、任务重，部分教师为了顺利完成教学计划，提出问题后或是让学优生直接给出答案，或是自己直接讲解，没有给学生提供足够的思考时间，使得课堂提问流于形式，不仅难以发挥课堂提问的优势，而且容易给学生造成心理负担，得不偿失.

1.3 问题缺乏质量

教师设计的问题既要紧扣教材，又要符合学生的心理特点和认知规律，还要有明确的目标，这样才能通过提问诱发学生思考，促进学生思维发展.然而，部分教师在设计问题时往往忽略了这一点，仅仅让学生回答“是不是”“对不对”“会不会”或“是什么”“为什么”等显性知识，问题缺乏思维量，难以促进学生的思考.

2 高职数学课堂有效提问策略

在注重学生学科核心素养培养的背景下，数学课堂要打破死记硬背、机械训练的现状，为学生营造一个平等、自主、和谐、探究的学习环境，鼓励学生探究思考，并提供机会让学生自主表达，逐步提高学生发现、提出、分析和解决问题的能力.在具体实施过程中，教师要在合适的时机提出有效问题，促进学生思考.

2.1 在“联结点”提出问题

数学学习是一个不断完善与发展的过程，有效的学习是建立在学生已有知识经验的基础之上的，教师作为课堂教学的组织者，要善于在新旧知识的联结点设问，为新知与旧知搭建互通的桥梁，促进旧知的巩固和新知的生长，构建新的认知结构，逐渐带领学生走上反思总结之路.

例如，在教学“函数奇偶性的定义”时，为了帮助学生更好地理解新知，建构新的认知结構，教师从学生已有的知识经验出发，精心设计问题，以期通过有效提问唤醒学生的已有认知，提高学生学习信心.问题如下：如图1，观察两个函数的图象，并回答下列问题.

（1）分别求当自变量x=±1和x=±2时的函数值，并说说你的发现.

（2）从对称的角度来分析，你有什么发现？

从学生已有知识经验出发，让学生通过观察、对比发现蕴含其中的一般规律，此时教师给出奇偶函数的定义，学生自然也就易于理解和接受了.

在日常教学中，若直接从课时视角出发，将课时内容生搬硬套地传授给学生，学生能够识记和套用，但是因为没有知识经验的铺垫，不仅不易于学生理解和掌握，而且难以帮助学生建构完善的知识体系，这样学生所掌握的知识是零碎的、分散的，难以形成持久的记忆，影响学习效果.因此，在实际教学中，教师要找准新旧知识联结点进行提问，以此通过问题将新知与旧知有效地串联起来，这样不仅可以及时巩固旧知，而且可以引出新知，有利于知识的理解，有利于知识结构的建立.

[HJ1.6mm]

2.2 在“冲突点”提出问题

新课标强调，课堂教学应激发学生的兴趣，调动学生的积极性，引发学生的思考，培养学生的创造性思维.为了达到这一要求，教师可以尝试制造一些冲突，并引导学生解决冲突，让学生经历从认知平衡到认知不平衡再到认知平衡的过程，这个过程可以激发学习兴趣、引发深度思考、发展数学思维、提升数学素养[2].

例如，在教学“组合”时，教师设计如下问题：

问题1 高一（5）班共有60人，从中任选5人参加演讲比赛，共有多少种选法？

在学习组合问题前，学生已经学习了排列，为此问题给出后，学生首先想到的是排列，而题目中给出的是“任选”，显然与学生已有认知冲突，学生因为不知道是否需要排列而产生困惑.面对学生的困惑，教师提问：若将“任选5人参加朗诵比赛”改为“任选5人参加不同的比赛”，你能得到什么？学生毫不犹豫地给出答案：A560.

问题2 题目改编前后，二者之间存在什么关系？

教学中，为了降低问题的难度，提高学生的参与度，教师鼓励学生合作学习，以此通过合作让学生相互启发、相互帮扶，探寻问题的突破口.通过合作学习，学生很快找到了解决问题的突破口，确定可以分步研究.首先从中任选5个人参加比赛是一个组合问题，而5人若参加不同的项目则是排列问题，这样结合排列知识顺利地解决了问题1，即C560=A560A55.

在日常教学中，教师要有意识地制造冲突，引导学生关注不同知识的区别与联系，以此通过“冲突”的解决，帮助学生深化认知、实现知识的相互融通，提高举一反三的能力.

2.3 在“交汇点”提出问题

数学是一门逻辑性较强的学科，数学知识前后有着千丝万缕的联系.教学中，教师要有意识地通过设问将相似、相关的知识建立联系，让学生从整体上把握知识，提高综合应用数学知识解决问题的能力，发展数学素养.

例如，在教学“一元二次不等式”时，为了有效沟通其与二次方程、二次函数之间的联系，获得一元二次不等式的解法，教师设计如下问题：

问题1 已知一元二次方程ax2+bx+c=0（a>0）的两个根分别为x1，x2，且x1≤x2，Δ=b2－4ac，请分别画出对应二次函数y=ax2+bx+c（a>0）的图象.

问题2 结合函数图象，你能写出不等式ax2+bx+c>0和ax2+bx+c<0的解集吗？

通过以上问题将三个“二次”有效地联系在一起，这样通过问题的解决不仅可以达到深化认知、加强理解的目的，而且可以优化学生知识结构，形成系统的解决方法，提高学生思考运用能力.

2.4 在“模糊点”提出问题

数学知识具有高度的抽象性，学生在理解上容易出现模糊点，甚至误区，若教师不能及时把握，很容易引发错误，从而影响学生学习效率和学习信心.基于此，在日常教学中，教师应根据学情从不同的角度设计问题，帮助学生消除盲点或误区，形成正确的认知，提高教学质量.

例如，在学习“双曲线”時，很多学生容易将双曲线的定义与圆、椭圆的定义相混淆.教师弄清造成混淆的原因，并在模糊点设问，以此通过问题的解决帮助学生消除困惑.

问题1 若双曲线定义中其他条件不变，仅将“小于|F1F2|”改为“等于|F1F2|”，此时点的轨迹是什么？

问题2 若双曲线定义中其他条件不变，仅将“小于|F1F2|”改为“大于|F1F2|”，此时点的轨迹是什么？

这样在“模糊点”设问，引导学生自主探索，主动对比，不仅可以顺利地消除模糊点，突破难点，而且可以提升学生的思维能力，切实提高学生分析和解决问题的能力.

总之，在数学教学中，教师切勿急于求成，要认真分析教材和学生，了解学生在学习中可能出现的问题，并结合实际情况有效提问，引导学生思考探究，帮助学生形成正确的解题方法，发展学生的数学思维，让数学课堂呈现勃勃生机.

参考文献：

[1]杨秀珍.浅谈高中数学教学中有效提问的重要性[J].现代农村科技， 2020（4）：121.

[2]许燕萍.利用认知冲突 解开学生数学素养生长的密码[J].数学之友，2023（12）：50-52.