融入概率学习的混合差分进化算法求解绿色分布式可重入作业车间调度

胡 蓉,伍 星,毛剑琳,钱 斌

(1.昆明理工大学信息工程与自动化学院,云南昆明 650500;2.云南机电职业技术学院,云南昆明 650000;3.昆明理工大学机电工程学院,云南昆明 650500)

1 引言

绿色制造作为同时考虑环境和能耗的生产模式,是工业生产实现高质量、可持续发展的重要环节.近年,中国碳达峰、碳中和“双碳”目标的提出和推行,对我国能源及制造业在节能减排方面提出了更高要求.企业要在竞争激烈的市场中胜出,生产成本的有效控制是关键.如何对生产过程进行优化调度实现降本增效,已成为企业的生命线.此外,公司之间生产合作和企业兼并现象日益普遍,分布式制造已经成为一种重要生产模式[1].在上述背景下,有必要深入开展绿色分布式生产调度方面的研究.

作业车间调度问题(job shop scheduling problem,JSSP)是工业生产中一类非常重要的问题.经典JSSP的研究通常局限于工件在各机器或设备上只加工1次.然而,在钢铁生产、半导体制造等战略性行业中,部分关键工件需在同一机器上处理多次(如钢卷退火和晶圆加工)[2].这表明研究绿色分布式可重入作业车间调度问题(green distributed reentrant JSSP,GDRJSSP)的建模与求解,具有重要现实意义.在计算复杂性上,JSSP归约于GDRJSSP,而JSSP属于典型NP难问题,故GDRJSSP也为NP难问题.因此,研究该问题也具有显著理论价值.

绿色生产调度的已有研究主要聚焦于单工厂或车间调度问题,包括绿色单机调度问题[1]、绿色并行机调度问题[3]、绿色流水车间调度问题[4]、绿色混合流水车间调度问题[5]、绿色作业车间调度问题[6]和绿色柔性作业车间调度问题[7].在分布式工厂方面,已有研究还较为有限,主要为绿色分布式流水车间调度问题[8]、绿色分布式装配流水车间调度问题[9]、绿色分布式作业车间调度问题[10].对于GDRJSSP,尚无研究报道,故亟需对其开展研究.

生产调度问题多为NP难问题,具有非凸几何结构,其主要求解算法包括运筹学算法和智能优化算法.运筹学算法(如分枝定界、列生成、分枝定价)追求获取问题最优解.然而,对于非凸优化问题,至今还没有多项式时间可获取最优解的通用算法.这使得运筹学算法需遍历或部分遍历问题解空间,从而无法在较短时间内得到较大规模问题的满意解.智能优化算法追求尽快获取问题优质解,其特点在于可通过对解空间较少区域的搜索来实现对目标值较广且较优区域的搜索[11].这使其能在较短时间内获取问题的优质解,从而成为目前求解各类复杂调度问题(包括文献[1,3-10]的问题)的主要算法.

差分进化(differential evolution,DE)算法将群体中个体间差异和竞争产生的群体智能用于优化搜索方向,具有较强的全局搜索能力和内在的并行搜索特性,被成功用于有效求解各种复杂优化问题[12].DE的研究受到众多学者的关注,已成功应用于求解交通运输、电力系统、化工制药等领域中的优化问题求解.在生产调度问题求解方面,现有的有效DE均采用混合算法框架,即利用DE对问题解空间执行全局搜索,同时根据问题特点加入合适的局部搜索,从而形成某种混合DE.譬如,Wang等[13]提出一种离散DE求解阻塞流水车间调度问题,其优化目标为最大完工时间最小.Wu等[14]针对分布式装配柔性作业车间调度问题,设计结合模拟退火的混合DE进行求解,以实现提前/延迟和总成本同时最小.对于GDRJSSP,目前没有基于DE的求解算法研究,故本文设计混合DE进行求解.

综上,本文提出一种融入概率学习的混合DE(hybrid DE incorporated with probabilistic learning,HDEPL),用于求解优化目标为同时最小化总完工时间和总能耗的GDRJSSP.首先,分析问题特点,设计编码规则来确定搜索空间,并设计活动化解码规则来提升解的质量.其次,采用DE执行全局搜索,同时加入基于贝叶斯网络结构的多维概率模型合理学习和积累优质解(即当前种群中的较优解)的模式信息,提升算法驱动全局搜索较快探测或感知到解空间中优质解区域的能力.下一步,分析问题解的结构特征,设计基于关键路径的4种邻域结构来对当前非劣解集中各非劣解执行较深入的局部搜索,进而利用基于非关键路径的节能策略尝试降低各非劣解对应的总能耗.最后,将算法应用于各种规模的测试问题进行对比分析,验证了HDE-PL能够有效求解GDRJSSP.

2 问题描述

2.1 GDRJSSP描述

GDRJSSP可描述为:考虑n个工件J={J1,···,Jn},分别分配到F个工厂上加工,每个工厂均有m台加工机器M={M1,···,Mm},每台机器存在s种可调节的速度档位且对应加工速度表示为V={v1,···,vs}.按工艺要求每个工件需要重复加工L次,即工件Ji的第j道工序用Oi,j来表示,工件Ji完成加工工序{Oi,1,···,Oi,m×L}的数量是m×L,相应的基本加工时间为pi,j.由于机器的加工速度可调整,当机器以速度vz加工工序Oi,j时,实际加工时间为pi,j,z=pi,j/vz.设工序Oi,j的开工时间为Si,j,完工时间为Ci,j,工厂k的完工时间为Ck,工厂k中机器Mj的开工时间为Sj,k.当机器Mj以速度vz加工时,单位时间能耗为EPj,z.当机器Mj上未加工工件时,则该机器处于待机状态,其单位时间能耗为EIj.令π={π1,···,πn×m×L}为整体的工序序列,为工厂f中的工序序列,nf为分配到工厂f中的工件数,其中

同时,生产环境设定为:在零时刻即可加工,即工件到达时间设置为零;机器间缓冲区大小不受限制;机器可采用数个档位分别进行匀速加工,每台机器只能完成一道工序的加工;每道工序需在前一道工序加工结束后才可加工;不能打断工序在机器上的加工.优化或调度目标是确定工件在工厂上的分配情况、各机器上工件工序在加工顺序以及机器速度设置,使得生产效率指标Cmax和总能耗指标(total energy consumption,TEC)达到最优.基于以上描述,建立如下数学模型:

其中: 式(1)为优化目标,即要求最大完工时间和总能耗同时最小;式(2)保证每个工件都能唯一分配到一个工厂中;式(3)-(4)保证同一工件的所有操作都必须分配到同一工厂中且工件的操作满足工艺约束;每台机器的首个加工工件由式(5)确定;工件在机器上加工顺序的唯一性由式(6)保证;式(7)-(8)限定任意时刻一个工件最多只能在一台机器上处理;式(9)限定一台机器最多只能同时处理一个工件,其中Q为极大的正数;式(10)确定每台机器的开始加工时间;式(11)确定每个工厂的完工时间;式(12)-(13)确定最大完工时间Cmax;式(14)限定任意时刻一个操作仅能在同一速度下进行处理;式(15)计算加工状态;式(16)计算待机状态的总能耗,其中ψj为机器Mj的能耗系数;式(17)计算加工过程中的总能量消耗.此外,设置二进制决策变量xr,i,j,k,yi,t,j和hi,j,z.若工件j为工厂k中机器Mj上加工工件r的后继工件,置xr,i,j,k=1,否则xr,i,j,k=0;若工件i在机器Mt上完工后继续在机器Mj上加工,置yi,t,j=1,否则yi,t,j=0;若工件i的第j个操作Oi,j以速度vz处理,置hi,j,z=1,否则hi,j,z=0.

2.2 Pareto最优

GDRJSSP需同时考虑最小化生产效率指标及能耗指标,属于多目标优化问题.该类问题需通过支配关系来确定最优解集.关于多目标优化中的支配、非劣解、非劣解集、Pareto最优解集等概念,可参见文献[15].在求解NP难的多目标优化问题(如GDRJSSP)时,智能优化算法追求在较短时间内获取尽量逼近Pareto最优解集的优质非劣解集.

3 融入概率学习的混合DE算法(HDE-PL)

GDRJSSP需将工件分配给不同的工厂并确定各工厂内的工件加工顺序,同时还要确定各工厂内机器的加工速度.因此,采用三元组(π,A,V)来表示HDE-PL的个体(即问题的可行解),其中π为工序序列,A为工厂分配向量,V为加工速度矩阵.

智能优化算法均是采用相应机制不断生成新个体或新解来实现搜索的.在HDE-PL的全局搜索部分,采用DE进化机制改变当前个体中的π来生成新个体,并利用概率学习模型采样机制生成与当前个体中的π和A均不同的新个体,同时用较优新个体替换旧个体并更新非劣解集,从而逐步引导搜索前往问题解空间中存在优质解的区域.在HDE-PL的局部搜索部分,先采用多邻域变换机制尝试改进当前非劣解集中每个解(对应存在优质解的区域)中的π,再利用调速节能机制尝试改进这些解中的V,从而生成更优的新个体.HDE-PL正是通过上述机制不断合理变换π,A和V的取值,从而实现对GDRJSSP解空间的搜索.

3.1 编码

工序序列π的编码方式为基于工件的工序编码,即π={π1,···,πn×m×L}(实例见表1最后1行).

表1 调度解的表达Table 1 Illustration of scheduling solution

在采用DE生成新个体时,当前个体中的A和V保持不变,只对π进行改变.然而,标准DE的个体为实数向量,只能在连续域空间内进行搜索.为使DE 可求解GDRJSSP,利用可重入最小值排序(reentrant smallest order value,RSOV)规则[16],将DE 中的第i个实数向量Xi=[xi,1,···,xi,n×m×L]转换为工件的工序或操作序列πi=[πi,1,···,πi,n×m×L].根据RSOV规则,首先将Xi=[xi,1,···,xi,n×m×L]按升序排列后得到中间序列φi=[φi,1,···,φi,n×m×L],再将中间序列φi映射为工序编码序列πi.这里πi,k=「(φi,k-1)/n×m×L」+1,其中「*」为取整操作,如「3.54」=3.表1 给出n=2,m=1,L=3时Xi到πi的转换示例.

此外,工厂分配向量A和加工速度矩阵V的编码为:A中第i个元素ai表示工件i分配至工厂ai加工,V中第i行第j列的元素vi,j表示工序Oi,j的机器加工档位.图1为n=5,m=3,L=2,F=2,A=[1,2,1,2,2]时一个调度解的甘特图.

图1 GDRJSSP调度解的甘特图Fig.1 Gantt chart of GDRJSSP’s scheduling solution

3.2 解码

传统JSSP的解码规则主要有无延迟解码、半活动化解码、活动化解码.对于GDRJSSP的解,本文拓展现有的单工厂活动化解码规则并用于对其解码,以尽量缩减工序完工时间,具体步骤如下:

步骤1为使各工厂中工序的完工时间整体较小,每个工件在分配时优先分配至当前完工时间最小的工厂,依此规则确定工厂分配向量A.根据A将n个工件{J1,J2,···,Jn}依次分配到不同的工厂中.

步骤2各工厂内每台机器上的工序加工顺序确定后,计算每个工序加工的开始时间和完工时间.

步骤3根据式(13)(17)分别计算问题解π的最大完工时间Cmax和总能耗指标TEC.

3.3 概率学习模型

对于GDRJSSP的解(π,A,V),工序块定义为工序序列π中连续相邻的两道工序.显然,π由不同位置上的工序块所组成.为能有效学习优质解中π内部工序块的分布信息,设计统计工序块出现频次的贝叶斯网络(见图2),并以此构建工序块分布概率学习模型.通过采样该模型生成新种群来实现与DE不同的搜索,可丰富HDE-PL的全局搜索行为并增强其引导全局搜索到达优质解区域的能力.

图2 N-1层贝叶斯网络(工序块频次统计模型)Fig.2 N-1 layer Bayesian network(statistical model of process block frequency)

3.3.1 频次统计矩阵

3.3.2 概率学习模型

为{BPop1,···,BPopG}的个体中第x位置和第x+1位置上工序块的累计概率分布,

3.4 全局搜索

如前所言,全局搜索靠DE进化机制和概率学习模型采样机制分别生成新种群来实现.DE生成新种群的过程见第2.6节的HDE-PL算法流程.概率学习模型采样生成新种群的过程如下.

3.5 局部搜索

GDRJSSP属于复杂的多目标组合优化问题.由于不同优化目标间的相互制约,优质非劣解通常聚集在庞大解空间中接近底部的不同区域,这增大了搜索难度.为提升算法性能,设计如下局部搜索对优质解区域进行更加深入细致的搜索.

GDRJSSP的关键路径为各工厂的关键路径中最长的一条.以第3.1节中图1和本节图3为例,工厂1和工厂2的关键路径分别为各自工厂中红线所连工序.由于工厂1的关键路径最长,故整个问题的关键路径为工厂1 的关键路径.结合甘特图分析GDRJSSP的解内部结构可知,该问题任何解的最大完工时间Cmax等于其关键路径的长度,故调整关键路径上的工序有较大概率能减小Cmax.因此,设计基于关键路径的4种邻域搜索(对应4种邻域结构),对每代种群中的部分个体分别执行由这4种邻域结构构成的变邻域局部搜索,以尽量减小这些个体的Cmax.进而,设计非关键路径的节能策略,尝试降低执行过局部搜索的个体的总能耗TEC.

图3 关键路径和调速节能Fig.3 Critical path and speed regulation for saving energy

3.5.1 多邻域贪婪搜索

基于关键路径的4种邻域搜索如下:

1) 关键工厂内Interchange: 随机选择1个关键工序,并将其与该工厂内所有的非关键工序逐一进行交换,形成个邻域,并输出最好邻域.

2) 关键工厂内Insert: 随机选择1个关键工序,并将其分别插入到该工厂中每个非关键工序之前或之后,形成个邻域,并输出最好邻域.

3) 工厂间Interchange: 随机选择1个关键工序,并将其与各非关键工厂中所有的工序逐一进行交换,形成个邻域,并输出最好邻域.

4) 工厂间Insert: 随机选择1个关键工序,并将其分别插入各非关键工厂中每个工序之前或之后,形成个邻域,并输出最好邻域.

基于上述定义,设计如下变邻域搜索.

步骤1为当前非劣解集中的每个个体或解确定1条关键路径,若有多条则随机确定1条.

步骤2逐一选择当前非劣解集中的解,并对其执行上述4种邻域搜索.每执行完1种邻域搜索后,判断新解(即输出邻域)是否支配旧解.如果是,旧解将被新解所取代,确定新解关键路径后对新解从刚执行过的邻域搜索开始,继续执行剩余的邻域搜索;若两个解互不支配,则将新解直接加入非劣解集,继续对旧解执行剩余的邻域搜索;若新解被旧解支配,则继续对旧解执行剩余的邻域搜索.

步骤3非劣解集中解的数量超过ps时,则删除拥挤距离较小的解[17],保持非劣解集大小为ps.

3.5.2 基于非关键路径工序降速的节能策略

对于GDRJSSP的任意解,通过保持各工厂中关键路径上工序的加工速度不变,对非关键路径上工序的加工速度进行降档调节,有可能在最大完工时间Cmax不变的前提下,实现总能耗的降低.基于这一问题特点,对执行变邻域搜索后的非劣解集中每个非劣解执行如下的调速节能操作:

步骤1确定各工厂中的关键路径.

步骤2判断各工厂的非关键路径上每道工序是否处于最低加工速度的档位.若是则转回步骤2继续判断下一道工序;若否则进行下一步.

步骤3将该工序的当前加工速度降低一档,并判断是否影响关键路径.若是则保持档位不变,转到步骤2继续判断下一道工序;若否则降低一档,转到步骤2继续判断下一道工序.

执行上述步骤对非关键路径上的所有工序完成降档尝试后,更新该非劣解的加工速度矩阵V.

3.6 HDE-PL算法流程

从以上算法流程可知,在HDE-PL的迭代搜索过程中,非劣解集TΩ在步骤10由DE和概率学习模型共同引导的全局搜索(步骤3-9)进行更新,同时在步骤12由结合变邻域搜索和调速节能操作的局部搜索进行更新.由于全局和局部搜索均得以加强,HDE-PL可实现对GDRJSSP解空间范围较广且具有一定深度的搜索.

4 实验设计与分析

4.1 实验设置

选择FT01,FT10,FT20,LA01,LA06,LA11,LA16,LA21,LA26,LA31这10个不同规模的JSSP标准测试算例,扩展得到适用于GDRJSSP的测试集(拓展算例命名为标准测试算例名称前加“E-”,见表2).在扩展测试集中,所有工件的重入次数设置为2次,加工阶段机器速度设置为5 个可调档位(对应加工速度为{1,1.3,1.55,1.75,2.10}),机器能耗系数设置为ψj=4,机器加工与待机能耗分别设置为EPj,z=4×vz2和EIj=1.所有算法采用Delphi XE10编程,运行环境为16 GB内存、i7处理器(3.20 GHz)的PC.采用如下指标比较算法性能:

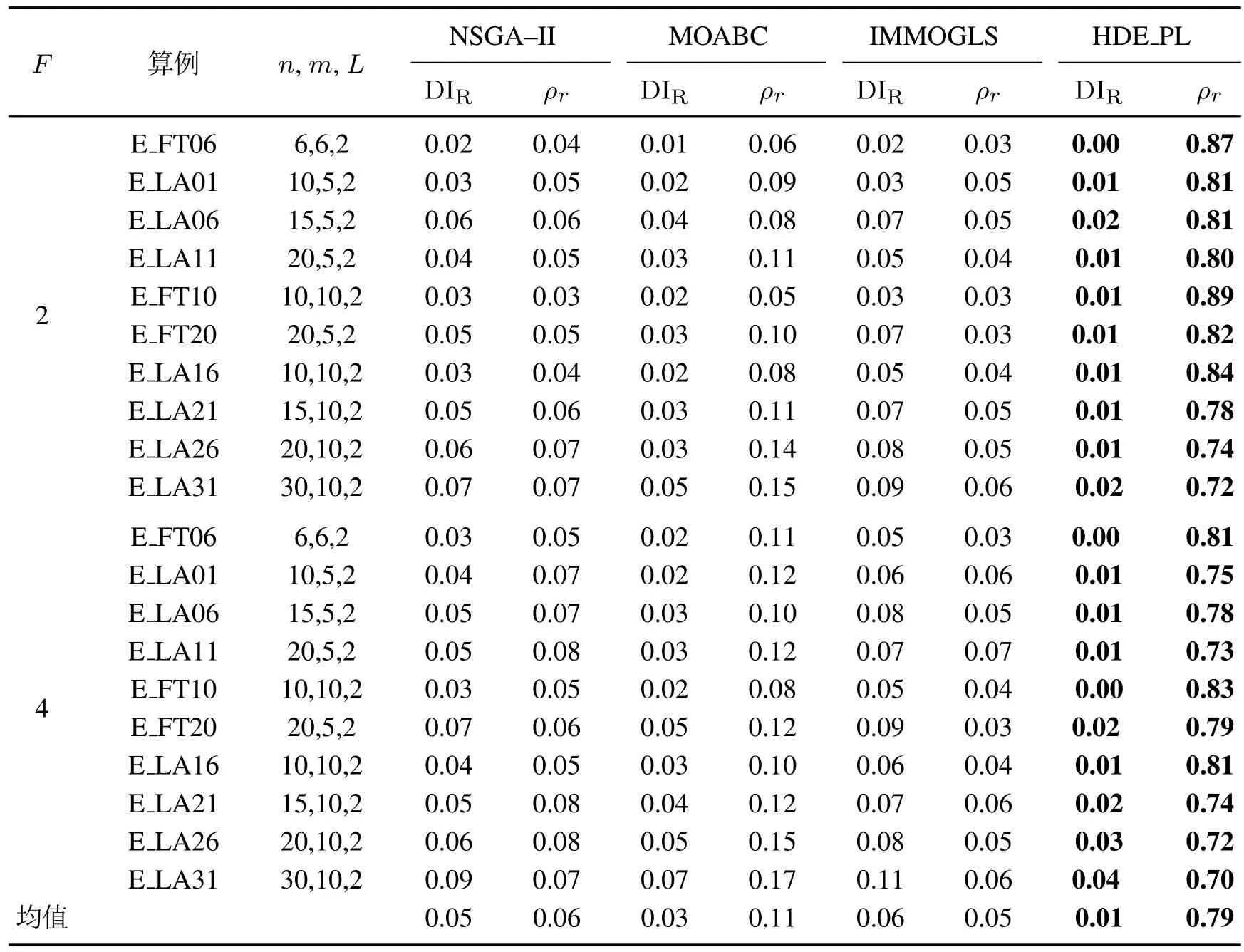
表2 NSGA-II,MOABC,IMMOGLS和HDE-PL的计算结果Table 2 Calculation results of NSGA-II,MOABC,IMMOGLS and HDE-PL

1) 距离指标DIR,可度量非劣解集Ω′中的元素相对于参考集Ω*的距离,即

其中: 解x ∈Ω′与解y ∈Ω*在归一化优化目标空间中的距离表示为d(x,y)[18].d(x,y)按式(29)计算:

式中:fi为第i个优化目标,分别为参考集Ω*中fi的最小和最大值.Ω*由所有比较算法得到的非劣解集合并构成.

2) 非劣解占比指标ρr,可度量由算法获得的非劣解集Ω′在Ω*中的比例.

DIR(Ω′)越小则表明算法获得的非劣解集更接近Pareto最优解集,而ρr越大则表明算法性能越强.

本文将HDE-PL 与非劣排序遗传算法(NSGAII)[17]、多目标人工蜂群算法(MOABC)[19]、改进多目标遗传局部搜索算法(IMMOGLS)[18]这3种高效多目标优化算法进行比较.多目标优化算法NSGA-II在离散和连续优化领域均应用广泛.MOABC在传统人工蜂群算法中加入数种有效局部搜索算子和交叉操作算子,可高效求解绿色多目标分布式作业车间调度问题.IMMOGLS采用随机加权和的方式处理多个优化目标,是公认的求解多目标流水车间调度问题的高效算法.在算法性能比较实验中,各算法运行时间均设置为f×n×m×25 ms,并都独立重复运行20次.评价指标DIR中的参考集Ω*由以上4种比较算法每次运行结束时输出的非劣解集合并得到.

4.2 仿真结果与比较

HDE-PL的关键参数为:种群规模ps、优势子种群比率φ、学习速率r1和r2、变异系数Fs、交叉概率CR.采用DOE实验设计法分析参数对HDE-PL全局搜索部分性能的影响.每个参数均选取5个不同水平值.对于每组参数,算法均运行10次,终止条件为f×n×m×25 ms.以算法在不同参数组合下各规模算例的ρr平均值作为评价指标,可得如图4 所示的参数响应图,故HDE-PL 的推荐参数组合为:ps=30,φ=0.3,r1=0.2,r2=0.1,Fs=0.5,CR=0.2.类似地,可得NSGA-II的推荐参数组合为:种群规模ps=30,变异概率pm=0.1,交叉概率pc=0.8;MOABC的推荐参数组合为:种群规模ps=30,放弃解极限La=50;IMMOGLS的推荐参数组合为:种群规模ps=30,精英个体数Ne=10,局部搜索概率pLS=0.8.

图4 HDE-PL各参数响应趋势图Fig.4 Response trend graph of HDE-PL’s various parameters

各算法在评价指标DIR和ρr下的测试结果如表2所示,其中最好值以粗体表示.由表2可知,HDE-PL的DIR值在所有问题上小于其他3种算法的DIR值,同时HDE-PL的ρr值也明显大于其他3种算法的ρr值.这表明HDE_ PL获得的非劣解集整体更接近于参考集,且获得的优质非劣解数量更多.为直观表现算法间的性能差异,图5给出这4种算法在算例E_ LA16(F=2)上的非劣解占比指标ρr对应的小提琴图(在其他算例上可得类似的图).从图5也可看出HDE PL在统计意义上显著占优.

图5 3种算法求解ELA16(F=2)算例的非劣解分布图Fig.5 Distribution of non-inferior via three algorithms for solving the E-LA16(F=2)

相对于NSGA-II 仅靠全局搜索驱动算法寻优,HDE-PL采用全局搜索和局部搜索结合的混合模式,可以更好兼顾搜索的宽度和深度.此外,虽然MOABC和IM-MOGLS两者也是包含全局搜索和局部搜索的混合算法,但是HDE PL的全局搜索部分结合分散搜索能力强的DE和引导性强的概率学习模型,有助于在更宽广的范围发现较多的优质解区域,同时在局部搜索部分采用基于关键路径的变邻域搜索,以便于执行更为集中深入的挖掘.因此,HDE PL具有更强的搜索引擎.

5 结语

本文在可重入作业车间调度问题基础上,进一步考虑分布式工厂场景和节能减排需求,确立优化目标为总完工时间和总能耗同时最小,进而建立绿色分布式可重入作业车间调度问题(GDRJSSP)模型.针对GDRJSSP,提出一种融入概率学习的混合DE(HDEPL)进行求解.在HDE-PL的全局搜索部分,设计DE与多维概率学习结合的协作搜索框架,有利于提升算法引导全局搜索到达解空间中优质解区域的能力.在HDE-PL的局部搜索部分,为实现对优质解区域较深入的细致搜索,设计相应的多邻域局部搜索.同时,为进一步降低总能耗,设计非关键路径工序加工降速的节能策略.仿真实验验证了HDE-PL的有效性.未来工作为设计高效HDE-PL 求解GDRJSSP 和物流集成的调度问题.