面向锂电池少量循环的二维支持域直推式健康状态预测
王一航,冯良骏,赵春晖
(浙江大学控制科学与工程学院,浙江杭州 310027)
1 引言
近年来,锂离子电池因其高能量密度、低自放电率、高电压、长寿命周期以及更高的可靠性被广泛使用[1],但同时,其带来的安全问题不容小觑[2].作为保障安全性的主要手段之一,锂电池的健康状态(state of health,SOH)管理受到越来越多的关注.SOH作为一种评估电池老化程度的指标,反映了电池实际容量与标称容量的衰减比率,由式(1)表示,其中Cact和Cnorm分别代表电池的实际容量和标称容量[3].
对于一个确定的电池,其Cnorm是确定的,故对SOH的预测可以转化为对Cact的预测.一个全新电池的SOH值为100%.随着电池的不断使用,SOH会逐渐下降.通常情况下,当电池的容量下降到初始值的80%,即SOH为80%时,视为寿命终止(end of life,EOL),应该更换电池[4].
一般情况下,准确的SOH只能在实验室条件下直接测量,实际应用中只能通过其他的变量例如电压电流进行估算.而由于电池老化的非线性和不确定性,SOH的预测变得十分困难[5].为解决此问题,近年来已经提出了很多预测SOH的方法,主要可以分为两类,机理分析法和数据驱动法[6].
机理分析法使用微分方程等方式来模拟电池运行状态下的电池老化过程,从而对SOH进行估计.Weng等[7]借助电化学模型和恒定电流-电压充电方法,使用变换函数和非线性最小二乘法对SOH进行预测.该模型结合了化学/电化学动力学和线性传输关系,以产生比经验模型更准确的预测.Li等[8]使用单粒子模型(single particle model,SPM)对SOH进行预测,该模型将阳极和阴极分别视为具有与电极相同的表面积的单个颗粒.卡尔曼滤波器(Kalman filter,KF)是一种自适应方法,也经常被用于SOH估计.Wassiliadis等[9]使用扩展卡尔曼滤波器进行SOH预测.卡尔曼滤波器在电池管理系统(battery management system,BMS)中应用非常广泛,其还被用于估计电荷状态(state of charge,SOC)、容量或者内部电阻[10].然而,基于微分方程的模型计算开销往往较大,且对专业知识的要求较高,很难精确地模拟整个老化进程.
数据驱动法通过利用历史充放电循环数据建立电池外部特征和SOH值的映射关系来预测SOH.该类方法不要求使用者了解内部的复杂机理,并且模型也可以在线应用[11].因此,近年来数据驱动的方法在学术界和工业界都越来越被广泛关注.例如,You等[12]使用神经网络方法预测SOH,平均误差小于2.18%,Klass等[13]提出了一种基于车载可用电池数据的SOH估计方法,使用支持向量机方法进行预测.Li等[14]通过电池充电曲线提取了特征,并且使用增量容量分析对特征进行选择,最后使用随机森林方法进行SOH预测.赵光财等[15]使用贝叶斯正则化神经网络对锂电池SOH进行预测,同时引入K临近-马尔科夫修正策略对预测结果进行修正.组合预测模型对锂电池SOH的平均预测误差小于1%.
尽管很多的数据驱动方法已在SOH评估任务中得到了广泛关注,但是该类方法需要依靠大量的历史数据进行训练.而在实际场景中,当历史充放电循环数据积累较少时,往往已经迫切地需要给出后续的SOH预测,但是锂电池的一次充放电时间往往需要花费数小时甚至数天,如果希望收集足够的电池老化数据进行建模,无疑需要巨大的时间成本[16].此外,锂电池在充放电循环中还会发生容量再生现象,容量再生现象是锂离子电池退化过程中的一个典型特征,如果电池在老化过程中的静置时间比正常的静置时间长,则会开启电池的恢复过程,从而可以增加下一个周期的可用容量,导致模型的预测不可靠[17].基于以上分析可以发现,在真实场景中对锂电池进行SOH预测,会受到典型的少数据问题的影响.如何在少量充放电循环数据的情况下巧妙设计建模分析策略,确保模型的预测精度,以及如何充分利用训练样本的信息,针对待预测样本有效进行建模,是笔者迫切需要考虑的问题,具有重要的理论研究价值和现实意义.
近年来,随着一些迁移学习方法例如域自适应神经网络(domain adaptive neural network,DaNN)[18]、细粒度域自适应对抗网络(fine-grained adversarial network-based domain adaptation,FANDA)[19]、相关性对齐(correlation alignment,CORAL)[20]和深度适配网络(deep adaptation network,DAN)[21]的提出,迁移学习算法已被广泛用于不同工业领域中.例如,在故障诊断方面,Chai等[22]提出了一种故障原型适配网络用于工业智能故障诊断,并利用多源域细化的对抗性适应策略解决域不一致和类别不一致下的故障诊断问题[23].近期,迁移学习算法也逐渐被用于锂电池SOH的少量数据预测问题.例如,Shen等[24]使用来自8个电池的源域数据训练了一个集成CNN模型,再根据目标数据集对模型进行微调,Ye等[25]使用对抗学习的方法使得源域和目标域通过特征提取器提取到的特征保持一致,最后使用少量目标域的数据对模型进行微调,Han等[26]提出了一种端到端的考虑域适应的增强长短期记忆(long short term memory,LSTM)迁移方法,采用了数据增强的方法使得源域和目标域的数据量相当,进而用最大平均差异(maximum mean discrepancy,MMD)约束实现域特征对齐.上述方法的主体思路均是使用其他工况的源域数据进行预训练,再利用目标域工况的数据进行迁移,没有考虑利用同一工况下已有电池的信息,在实际中不同工况的数据差异极大,电流、温度,甚至充放电方式都可能有所改变,导致模型的迁移困难.在这种情况下,如果能够利用已有的同一工况下其他电池的数据作为扩充,根据待预测电池的特性对数据进行选择,则会有充足的数据进行建模,实现对SOH的精准预测.
针对上述问题,本文提出了一种二维支持域直推式建模方法(two-dimensional region of support transductive learning,2D-RoSTL),通过对数据由粗到细的精确划分及模型搭建,实现了少量充放电循环下SOH的准确预测.一方面,利用同一工况其他电池的相似特性作为数据扩充,用批次数据和历史数据在两个维度上构造支持域,对数据进行粗划分,提供了充足可供选择的样本;另一方面,提出了一种直推式学习框架,考虑离线样本和在线样本特征空间的相似性信息,实现了少量循环数据下样本的精细化充分利用.并且,本文提出的方法不拘泥于特定数据,是一种通用的结构范式,其可以适用于任何具有批次数据的少量循环SOH预测场景中.本文的贡献点总结如下:
1) 提出了一种针对少量充放电数据的二维支持域构造范式,能够解决历史数据不充分的情况下模型过拟合问题以及容量再生现象导致的预测不可靠问题,其思想方法为该领域典型少量数据问题的解决提供了新的研究思路;
2) 提出了一种关注样本特征空间内相似性信息度量的直推式框架,扩充模型信息来源,细化了样本的重要程度,保证数据信息的充分利用,从而实现了对少量数据下SOH的精确预测.
本文结构如下: 第2节首先介绍了少量数据场景下的建模问题,包括使用的数据以及待解决问题的阐述;第3节介绍了本文提出的2D-RoSTL方法,包括二维支持域的构造、特征提取以及直推式建模策略;第4节通过实验证明了所提二维支持域直推建模方法的有效性;第5节进行了总结与讨论.
2 少量数据下的建模问题
在本节中,首先介绍了文中使用的4个NASA的电池数据,进而从数据出发阐述了少量循环数据情况下的建模问题.
2.1 数据介绍
本文中使用的数据集来自NASA的爱达荷州国家实验室[27],使用的电池编号为No.5,No.6,No.7和No.18.此组电池均在室温24°C条件下循环进行充电、放电和阻抗测试.在充电过程中,电池首先在恒流(constant current,CC)模式下以1.5 A电流进行充电,直至电压上升至4.2 V,然后进入恒压(constant voltage,CV)模式进行充电直至充电电流下降至20 mA.放电过程包含CC 模式,以2 A恒定电流的方式进行放电,直至电压下降至2.7 V,2.5 V,2.2 V和2.5 V.
图1展示了4个电池的老化曲线,从图中可以看出,电池的退化能力随着循环次数呈现不稳定的下降趋势,并且在循环过程中还有一定的容量再生现象.由于电池容量和电池循环次数之间的关系为非线性,这就使得电池SOH 的预测变得更加困难.图2 展示了No.6电池第10次充放电循环过程中的电压、电流和温度曲线,对于每一次充放电循环,采样点的个数都不尽相同,如何选取合适的特征对SOH进行预测,也是需要面临的一大挑战.
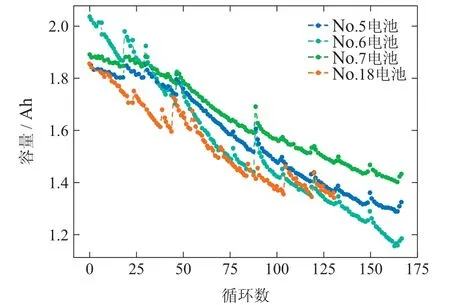
图1 4个锂电池的老化曲线Fig.1 Aging curves of four lithium batteries

图2 No.6 电池第10次充放电循环电压、电流、温度曲线Fig.2 No.6 battery voltage,current,temperature curve during the tenth charge and discharge cycle
2.2 少量循环数据建模问题
对于样本的SOH值,本文通过电压、电流、温度3个传感器的值对其进行估计.在本文中用表示第j个电池第i次循环的SOH值(后续均使用上标表示电池,下标表示循环次数),其中:i ∈{1,2,···,N},N为总循环数,j ∈{1,2,3,4}.分别表示第i次循环下电压、电流、温度曲线,j ∈{1,2,3,4}..t代表该循环下采样点的个数,三者均为时间的函数.用F(·)表示整个预测框架,则有
传统方法建立模型时使用的训练数据为之前积累的历史数据,设之前共积累了k轮充放电循环的历史数据,用分别表示历史数据的特征和标签,有
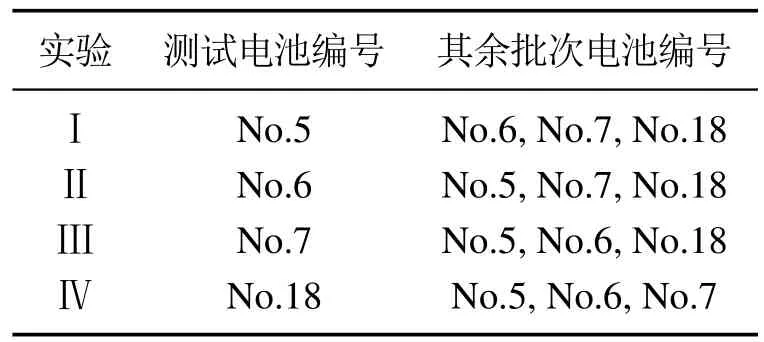
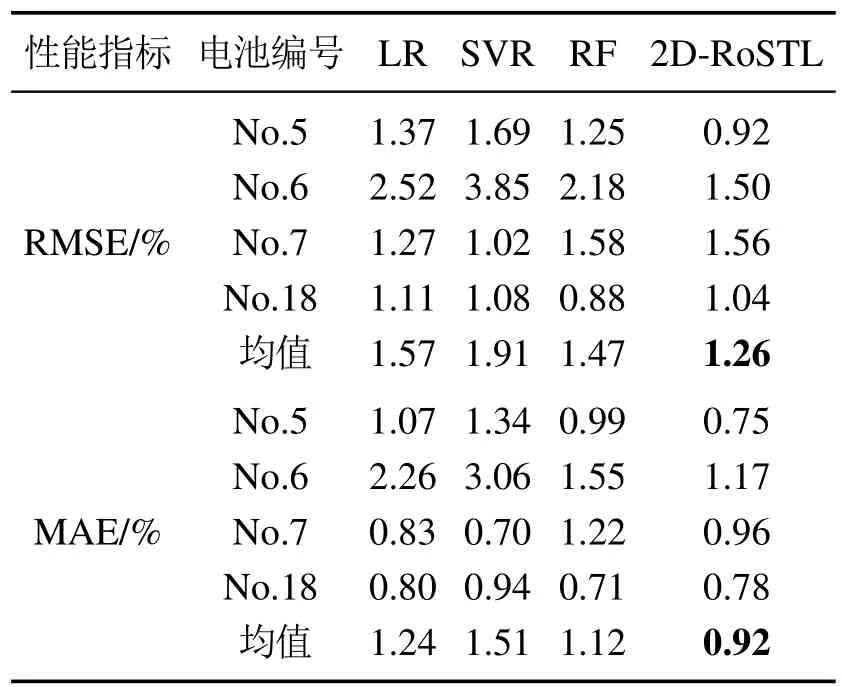
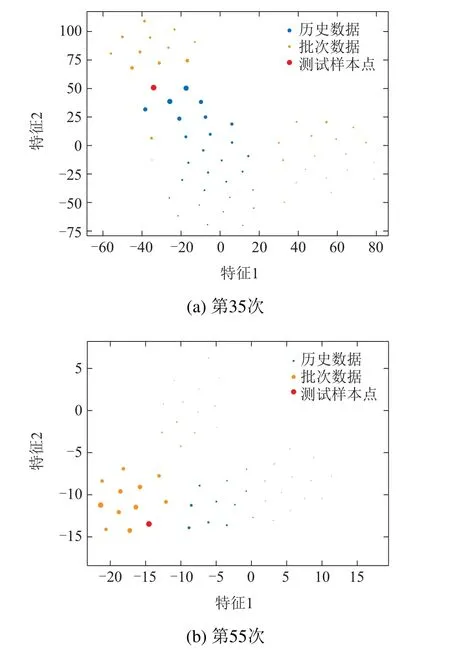
在模型建立完成后,如果希望预测第n轮充放电循环的SOH(k 图3 第n轮充放电循环训练数据示意图Fig.3 Schematic diagram of training data for the nth round of charge-discharge cycles 在本节中,首先介绍了本文所提出模型的整体结构,然后依次详细阐述了模型的各个部分,包括二维支持域的构建方法、通过传感器信号提取输入特征的手段和直推式建模以及在线应用的过程. 模型的整体结构如图4所示,首先,使用历史数据和批次数据在两个不同的维度上构造支持域,对数据进行粗划分.然后,将所选数据进行特征提取,通过滤波后的曲线提取了6个特征点.最后,直推式建模利用支持域中提供的数据,使用离线和在线样本点特征空间的相似性信息,对每个训练样本点再进行细划分,赋予每个样本不同的权重.模型建立完成后,预测测试样本点的容量,并计算SOH值.二维支持域的构建为后续建模提供了充足的数据,特征分析模块提取的特征点为模型提供了良好的输入支撑,而直推式建模利用了新样本点特征空间的信息,保证循环数据较少情况下信息的充分利用.整体结构由粗到细,模块之间相辅相成,共同完成SOH预测模型的搭建,以实现对SOH的精准预测. 图4 建模应用流程图,整体由特征提取、2D-RoSTL建模和在线应用3部分构成Fig.4 The modeling application flow chart is composed of three parts: feature extraction,2D-RoSTL modeling and online application 在少量充放电循环数据的条件下,如何避免模型的过拟合及预测不可靠,是笔者迫切要考虑的问题.本文借鉴了工业过程中的批次思想[28-31],将其首次创新性引入到SOH研究中. 图5展示了二维支持域的构建图,其由两部分构成,横向的历史循环数据和纵向的批次数据,其中两部分张成的空间构成了数据矩阵.相比传统建模方法仅使用历史数据建模,引入批次思想构造建模数据不仅仅增加了数据量,解决了模型训练数据不足的问题,更是从另一个维度上为模型提供了其他电池的参考信息,使得模型学习到更多不同情况下的知识,增加模型的鲁棒性以及泛化性能. 图5 二维支持域架构图Fig.5 2D region of support structure diagram 通过构造二维支持域补充数据后,还需要对数据进行处理.每一次充放电循环都会产生3条V,I,T曲线,考虑到电池老化的非线性,需要从曲线中提取和电池容量密切相关的特征作为输入进行预测. 增量容量(incremental capacity,IC)曲线[32]是近些年被用于提取SOH特征的重要手段,其纵坐标是横坐标是电压值,可由下式计算: 由于IC曲线涉及到微分计算,曲线中包含非常多的噪声信号,噪声会影响本文对特征的提取,所以,如何去除噪声就变得尤为关键.比较常用的方法有SG(Savitzky-Golay)滤波法[33]和高斯滤波(Gaussian smoothing,GS)法[34].图6比较了No.6电池第30个循环IC曲线由SG滤波器和GS滤波器滤波的效果.可以看出,GS滤波器的滤波效果更加优秀,其可以获得干净的峰值信号.故在本文中使用GS滤波器进行滤波,其可以表示为 图6 No.6 电池第30个循环IC曲线SG滤波器和GS滤波器滤波效果Fig.6 No.6 battery 30th cycle IC curve SG filter and GS filter filtering effect 其中:µ是均值,σ是标准差.使用GS滤波器滤波之后,从曲线上提取了6个特征点,分别是两个波峰和一个波谷的电压值和值,使用这6个特征对SOH进行预测,需要注意的是,均值和标准差的选择必须谨慎,如果过平滑可能使得曲线的波峰和波谷消失,如果平滑不足可能使得波峰和波谷增多. 二维支持域的构建相当于是对整体数据做了一次粗划分,为模型的建立提供了充足的样本,但是由于模型中包含历史和批次两个维度的数据,数据的地位并不等同,并且在同一个维度内部,例如建模的历史数据,一个样本和一个样本之间的重要性也不是完全相等的.如果将全部的数据给予相同地位进行建模,无疑会损失很多信息.本文这里利用在线样本和离线样本特征空间的相似性,扩充信息进行直推式建模,为每一个样本赋予一个独立的权重,细化每一个样本的重要程度,整体由粗到细,实现模型的精细化搭建和数据的充分利用.用xtest表示在线样本,模型变为 在SOH预测中,希望更多的关注那些对预测更有帮助的信息,更多的忽略那些可能携带噪声的信息.所以,这里采用特征空间中相似性度量的手段来判断训练样本的重要性,和xtest更加相近的样本认为其更加重要.样本权重通过高斯核函数进行计算,使用下标q代表训练集中的第q个样本,用w表示样本的权重 图7展示了基于特征相似性的直推式建模方法,其在构造二维支持域的基础上(图5所示)细化了支持域的范围,并且增加了样本权重.需要注意的是,这里的远近并不是指的距离的远近,而是通过式(14)使用特征之间的相似性进行度量,循环相近的样本之间特征也有可能相差很远,例如图中两点权重不同,循环更远的点反而权重更大一些.特别指出,可通过事先定义一个衡量权重大小的阈值.如果权重小到对建模没有影响,即低于该阈值,则这些数据点将会被忽略,从而支持域的范围也会发生改变,变为一个不规则的形状,从图中可以看出,支持域中已将权重小的点除去(如虚线部分所示),这些点一般为批次数据中偏远的点. 图7 基于特征相似性的直推式建模Fig.7 Transductive modeling based on feature similarity 由于提取到的特征和真实的SOH值相关性很高,故本文建模方法采用的是最小二乘法,损失函数取真实值和预测值的二范数平方,有 2D-RoSTL算法应用的整体过程如算法1所示,当一次充放电循环完成后,利用滑窗选取二维支持域,得到批次数据,加上原有的少量历史数据,经过特征提取和特征相似度权重计算后建立最小二乘模型D,最后将待预测样本进行特征提取后输入模型,即可得到预测的SOH值.需要说明的是,由于最小二乘模型建模及预测的时间为秒级,故在线进行建模完全可以保证预测的及时性和准确性. 算法12D-RoSTL算法. 输入:历史及其他电池充放电循环传感器信号V,I,T,每次循环所对应的SOH值y,待预测传感器信号Vtest,Itest,Ttest. 输出:预测的SOH值ytest. 步骤1通过二维支持域选取数据,根据式(8)-(9)截取待预测循环前后其他电池的批次数据; 步骤2将选取的数据和该电池之前的历史数据使用增量容量曲线和高斯滤波进行特征提取,得到用于训练; 步骤3将待测传感器信号进行特征提取,得到xtest; 步骤4使用式(14)计算训练集中每个样本的权重; 步骤5建模,最小化式(15)中的损失函数L,模型收敛或迭代超过最大次数时停止迭代,得到模型D; 步骤6通过模型D预测xtest对应的SOH 值ytest. 本节利用NASA的开源数据[27]对2D-RoSTL算法的有效性进行验证,使用的电池编号为No.5,No.6,No.7和No.18,具体充放电细节如第1.1节所述.由于此组电池的实验条件均相同,故将其视为同一工况下不同批次的数据.每一次对比实验共进行4组,每组选择一个电池作为测试电池(后续表中电池编号均指测试电池编号),取其前20%的历史数据作为训练,后80%的数据作为测试,其余电池作为批次数据的补充,共同进行2D-RoSTL建模预测,其实验数据集划分如表1所示. 表1 实验数据集划分Table 1 Experimental dataset partition 实验评价标准选用均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE).RMSE可以衡量观测值同真值之间的偏差,而MAE能更好地反映预测值误差的实际情况,二者可以用下式表示: 其中:yi代表真实值,代表预测值,M代表总预测样本数. 为了验证所提2D-RoSTL算法的有效性,首先,将其与一些直接建模模型作对比实验,选取了常用的线性回归(linear regression,LR)、支持向量回归(support vector regression,SVR)以及随机森林(random forest,RF)3种回归算法,它们均已被广泛用于锂电池SOH预测[16-17].实验中回归算法均使用测试电池前20%的历史数据和其余批次电池的全部数据集合作为训练,而2D-RoSTL则是采用划分的支持域中的数据作为训练.表2展示了几种算法对SOH的预测精度(均值最优用粗体表示),2D-RoSTL 在No.5和No.6电池上的预测有着最优的结果,并且在4个电池平均的精度上也保持最优.值得注意的是,这里滑窗的长度仅为11,相比较每个电池168次循环的数据长度,建立支持域所使用的批次数据不足整体的10%,但其效果却优于使用全部批次数据建模预测的其余回归算法,充分体现了本文所提方法的优越性. 表2 对比直接建模的回归算法预测性能Table 2 Comparing the predictive performance with regression algorithms for direct modeling 图8展示了回归算法和2D-RoSTL在No.5电池上的SOH预测效果,从图中可以看出,2D-RoSTL的预测值(紫色)和真实的SOH值(蓝色)最相近,其预测结果明显优于其余的回归算法. 图8 回归算法和2D-RoSTL算法在No.5电池上的SOH预测效果Fig.8 The SOH prediction effect of the regression algorithm and the 2D-RoSTL algorithm on the No.5 battery 为了证明2D-RoSTL在少量数据方法中的优越性,将所提算法与DaNN,CORAL和DAN 等迁移学习方法进行对比实验,迁移学习方法的源域为其他批次电池的全部数据,目标域为测试电池的前20%历史数据. 表3展示了迁移学习方法和2D-RoSTL的预测性能,在4组电池实验共10个RMSE和MAE指标中,所提方法有7次均为最优,其余性能也与最优结果相近,且平均精度也为最优(RMSE均值为1.26%,MAE均值为0.92%,而其余迁移学习算法最优RMSE 均值为1.74%,最优MAE均值为1.47%). 表3 对比迁移学习算法预测性能Table 3 Comparing the predictive performance with transfer learning algorithms 图9对No.6电池第35和第55次循环时的二维支持域分布以及训练数据样本权重进行可视化,从图中可以看出,对于不同的测试样本,其二维支持域的选取不尽相同,并且历史数据和批次数据的重要性也有所不同,对于前期的待测样本点,历史数据的重要性可能较大,而对于中后期的样本点,批次数据则是占主导地位,二者共同构成的二维支持域将待测样本点囊括其中,从而极大地提升了SOH预测的准确度. 图9 二维支持域可视化效果图Fig.9 The 2D region of support visualization 为了验证2D-RoSTL算法中各模块的有效性,设计了消融实验进行对比,其结果如表4所示. 表4 消融实验Table 4 Ablation experiment 表中二维支持域方法(2D-RoS)为本方法中去掉了直推式模块后的方法,其直接使用构造的二维支持域进行建模,不考虑样本权重.二维直推式方法(2DTL)为本方法中去掉了二维支持域模块后的方法,其不进行二维支持域的构造,而是直接使用全部的历史数据和批次数据进行建模.一维支持域直推式方法(1D-RoSTL)为本方法中将二维支持域替换为一维后的方法,其不使用历史数据,而是仅使用批次数据进行支持域的构造,其中最优结果加粗表示,可以看到,2D-RoSTL在除No.7电池之外的其余所有实验组中均表现最优,并且4组实验的误差均值也是最小,对于No.7电池,其与最优结果2D-TL误差接近,但2DTL算法建模是使用了全部的数据,而2D-RoSTL在每次建模构造支持域时仅使用了很少的数据,充分说明了2D-RoSTL各个模块的有效性. 本文针对锂电池SOH预测遇到的充放电循环历史数据不足与容量再生问题,创新性地提出了一种2DRoSTL方法,通过对数据由粗到细的精准划分,实现了基于少量充放电循环数据对SOH和再生现象的精确预测,其中二维支持域的构造范式可以拓展到其他的少样本学习问题中.通过NASA的数据进行了实验验证,2D-RoSTL方法对比其他的直接建模方法以及迁移学习方法都有显著的性能优越性,其在4个电池中RMSE 均小于1.56%,MAE 均小于1.17%,为少量数据的SOH预测提供了新思路.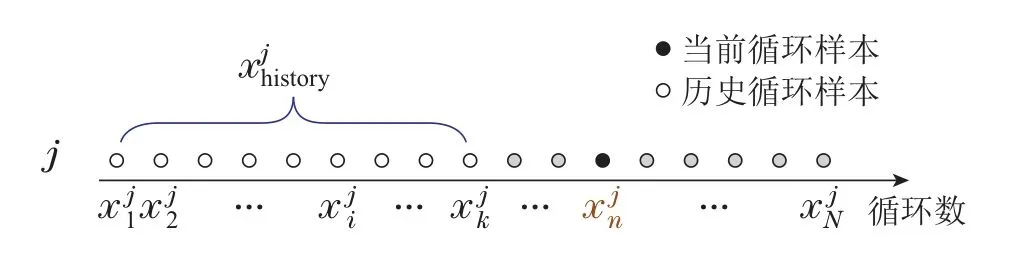
3 二维支持域直推式(2D-RoSTL)建模方法
3.1 整体结构
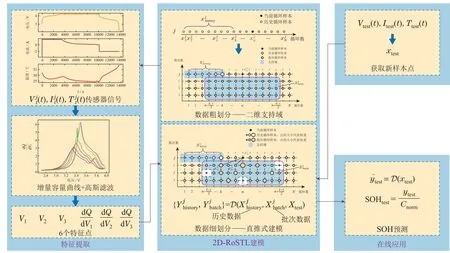
3.2 二维支持域的构建
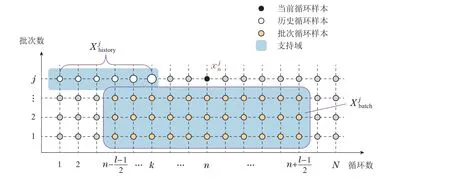
3.3 特征提取

3.4 基于特征相似性的直推式建模
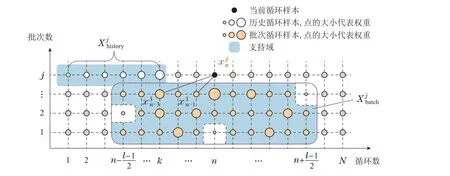
3.5 在线应用
4 实验与分析
4.1 数据集及评价标准
4.2 对比回归算法
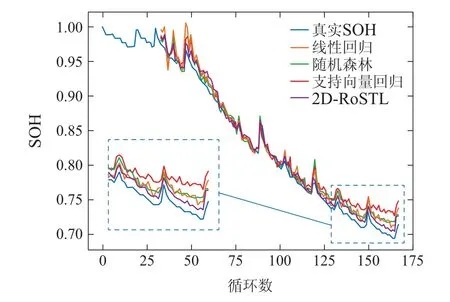
4.3 对比迁移学习算法及支持域可视化

4.4 消融实验

5 结论

