基于工况知识引导注意力时间卷积网络的烧结终点预测

方怡静,蒋朝辉,桂卫华,潘 冬

(1.中南大学自动化学院,湖南长沙 410083;2.南洋理工大学化学化工与生物工程学院,新加坡 637459)

1 引言

烧结是将贫铁矿加工成富铁矿有利于高炉冶炼的过程,生产的烧结矿为高炉炼铁提供主要原料,是钢铁企业的重要生产环节[1-2].烧结终点(burning through point,BTP)是指料层温度最高点所对应的烧结机位置.如果烧结终点超前,会造成烧结机利用率低;如果烧结终点滞后,混料未完全烧透便被破碎冷却,会造成烧结产品质量降低,返矿率升高,成本增加[3-4].因此,烧结终点的实时预测对实现烧结过程的稳定运行优化与控制具有重要意义[5-6].

烧结过程伴随着复杂的物理化学反应,内部规律复杂,具有较强的动态性和非线性,这使得数据驱动的烧结终点预测模型受到了广泛关注.针对烧结终点位置预测,国内外学者做了一系列相关研究.文献[7]采用灰色理论模型和粒子群算法预测烧结终点位置.文献[8]将遗传算法与神经网络相结合应用于BTP的预测.文献[9]提出了梯度提升决策树算法来建立BTP温度的预测模型.文献[10]通过烟花算法来优化模型参数,利用支持向量机构建BTP预测模型.文献[11]建立了集成极限学习机模型用于预测固体燃料消耗量、煤气消耗量、BTP和转股强度.上述方法虽然在烧结过程BTP的预测上取得了一定进展,但是它们大都是浅层网络,难以描述烧结过程数据内的复杂非线性和时空动态性.

时间卷积网络(temporal convolutional network,TCN)是近年来提出的一种具有时序数据处理能力的模型[12-13].通过膨胀因果卷积、空洞卷积等卷积计算方法,TCN具有更灵活、更长的感受野,这使它更容易捕获长期的历史数据特征信息.对于烧结过程,从装料操作到烧结结束需要几十分钟,伴随着复杂的物理和化学反应,烧结终点的位置受过去多个时刻的过程数据影响.然而,传统的TCN无法区分预测窗口内每个特征变量的重要性,没有考虑不同特征变量对烧结终点预测结果的重要性.

为此,本文提出了一种工况知识引导注意力时间卷积网络(attention mechanism temporal convolutional network,AM-TCN)用于烧结终点的智能预测.为了获取历史数据中包含的工况信息,本文利用导数动态时间规整距离,根据当前工况数据查询得到历史相似的工况数据,对历史相似过程数据进行分析,实现对历史工况知识的提取.为了获取过程变量序列与烧结终点位置之间的动态相关性,利用堆叠的时间卷积模块实现过程数据的特征提取,得到预测窗口内的过程数据序列的特征变量.为了区分每个特征对当前任务的贡献,引入注意力机制,通过计算得到的历史工况知识自适应地确定特征变量的注意力值,从而提高模型动态特征提取性能.基于某烧结厂的生产数据对所提方法进行了实验验证,结果表明所提方法具有较好的预测精度,可以为烧结现场操作人员控制烧结过程提供可靠的烧结终点位置信息.

2 时间卷积网络

时间卷积网络是为抓取长时依赖信息而提出的一种时序卷积神经网络模型.它主要由因果卷积和膨胀卷积两部分组成.因果卷积只利用输入时刻之前的时间序列参与运算,而不涉及未来的数据信息,从而保证了时序建模的因果性.膨胀卷积对卷积输入进行间隔采样,网络的感受野大小随着层数呈指数级增长,以适应高维情况下的序列输入.典型的时间卷积网络如图1所示.

图1 时间卷积示意图Fig.1 Schematic diagram of temporal convolution

定义输入时间序列表示为X=(x0,x1,···,xt,···,xT),卷积核表示为F=(f0,f1,···,fk-1),则膨胀卷积的计算方法如下所示:

式中:d表示控制卷积核之间间隔的膨胀率,k表示卷积核的大小,其感受野的计算公式为

感受野的大小随着膨胀率d的增加成倍扩大,膨胀卷积正是通过这种策略灵活调整感受野的尺寸.除了增加卷积层数,还可以通过堆叠时间卷积模块的方式来扩展感受野并提高卷积计算对输入序列的记忆能力.这种方式可以通过更少的网络层数获取更多的历史信息,因此被广泛运用.

为了缓解网络深度增加带来的过拟合和梯度爆炸等问题,TCN中还引入了深度残差网络中的残差结构来缓解上述问题.如图2所示,一个残差学习单元包含多个堆叠的网络层,每一个残差学习单元的输入x与输出直接相连,其数学表示为

图2 残差连接示意图Fig.2 Diagram of residual connection

其中:xl和xl+1分别表示残差单元的输入和输出;F(xl,Wl)是残差函数,表示学习到的残差;h(xl)表示恒等映射;最终残差单元的输出为F(xl,Wl)+xl.

通过扩张的因果卷积和残差连接,时间卷积网络可以灵活的调整感受野的大小,从而获取动态过程时间序列中包含的信息.为了充分挖掘数据的深层次特征,本文通过堆叠多个时间卷积模块来构建深度时序特征提取网络.每个时间卷积模块依次包含两个膨胀因果卷积层和一个激活函数,不同的时间卷积模块中会使用多个卷积核来进行特征提取.而在一个时间卷积模块内,两个膨胀因果卷积层具有相同的扩张率d和内核大小f.第N个时间卷积模块RFN上的感受野大小可以计算如下:

根据上述分析,利用堆叠时间卷积网络提取数据的非线性和动态特征可以看作是过程变量的潜变量.假设t时刻的终点预测值为y(t),则网络的输入为{x(t-T+1),x(t-T+2),···,x(t)},其中x(t)∈Rn.特征提取模块的输出为V={v1(t),v2(t),···,vm(t)}.

3 烧结终点预测模型的建立与分析

为了充分挖掘历史数据信息中有意义的工况知识和烧结过程数据的非线性和动态特征,本文提出了一种工况知识引导的注意力时间卷积网络用于烧结过程的烧结终点预测.本节将详细介绍所提方法的具体内容和其预测建模框架.

3.1 基于DTW距离的历史工况知识获取

目前,烧结厂的操作人员通过对历史工况数据总结专家知识,可以根据当前的过程数据结合相似的历史工况信息判断当前工况下大致的烧结终点位置.当前工况与历史工况的相似性可以视为当前过程数据序列与历史过程数据序列的相似性.衡量数据序列的相似度计算的方法众多,利用欧氏距离来比较两个时间序列时,序列与序列之间的每一个点按顺序建立起了一对一的对应关系,这种计算方式可能丢失两个时间序列关键波动特征的相关性.动态规整距离(dynamic time warping,DTW)方法可以在非一一对应的情况下成功匹配两个过程数据序列的波峰和波谷.而波峰和波谷可以反映时间序列的波动性,尤其是在工业过程中,过程序列的波动往往能够表征该段序列的重要特征.因此,DTW在时间序列轨迹相似性测量中具有显著的优势.给定两个时间序列Q={q(1),q(2),···,q(p)}和C={c(1),c(2),···,c(s)},构建一个p×s的距离矩阵,矩阵中的第i行第j列所对应的元素代表的是序列中点q(i)和q(j)的距离dE(q(i),c(j)),其中dE代表欧氏距离,dE(q(i),c(j))=(q(i)-c(j))2.DTW的目的是寻找最佳路径W={w1,w2,···,wk}以最小化Q和C之间的积累距离.积累距离dDTW(i,j)为当前点距离dE(q(i),c(j))与可以到达该点的最小的邻近元素的累积距离之和,表达式为

通过这种方式进行递归计算,可以得到最终的累积距离dDTW(q,c),即Q和C之间的DTW 距离dDTW(Q,C).然而,DTW会在对齐两个序列时产生不自然的扭曲,如图3所示,这主要是因为DTW算法仅考虑了数据点在纵坐标轴上的值而没有考虑数据的变化趋势.为了改善这一问题,Keogh等人[14]提出导数动态时间规则(derivative DTW,DDTW),通过计算时序数据的一阶导数来获取与序列形状相关的信息,这样能更好的捕捉时间序列数据波动信息.

图3 DTW对齐两个序列时产生的不自然扭曲[14]Fig.3 Unnatural distortion when DTW aligns two sequences[14]

在DDTW中,距离矩阵中的元素为时序数据在两点处一阶导数的差值的平方.DDTW中的一阶导数估计算公式如下所示:

而DDTW的累积距离计算公式为

DDTW距离的详细计算步骤如表1所示.

表1 DDTW距离的详细计算步骤Table 1 Detailed calculation steps of DDTW distance

同时,为了区分历史工况对工况知识的贡献度,定义以下权重计算公式用于计算各个历时数据序列包含工况知识的权重:

其中θ为控制权重随着距离变化快慢的可调参数.

通过计算当前输入过程数据序列与历史过程序列之间的DDTW距离,可以获得与当前工况相关度最高的历史工况数据序列,进而提取历史工况知识.具体的历史工况知识提取步骤如下:

步骤1获取历史采样输入数据序列{x(t-T+1),x(t-T+2),···,和输出数据{yT,yT+1,···,ykT};

步骤2通过DDTW距离准则计算当前输入数据序列{x(t-T+1),x(t-T+2),···,x(t)}与历史输入数据序列之间的距离以及权重值w=[w1,w2,···,wM],并选择M个最相关的数据序列作为历史案例库;

步骤3计算历史案例库中数据序列对应的输出数据计算得到历史工况知识.

3.2 基于工况知识引导的注意力机制计算

使用时间卷积对过程序列进行特征提取,提取的特征可以看作过程变量的潜变量.然而,提取得到的潜变量对预测目标的贡献并没有被考虑,因此,笔者希望能够区分不同潜变量的重要性.烧结终点的位置与当前的工况息息相关,通过查询历史数据库,可以获取与当前工况相似的历史工况,从而提取得到历史工况知识,提取得到的历史工况知识包含了当前工况的特征.因此,通过将历史工况知识引入注意力机制,可以充分挖掘历史数据中包含的工况信息与当前特征潜变量之间的相关性,从而获取不同潜变量对当前工况下的烧结终点位置的贡献,进而引导模型自适应的确定特征变量的状态.定义重构得到的特征变量为V={v1(t),v2(t),···,vm(t)}.将获取的历史工况知识作为先验知识引入注意力机制,实现基于工况知识引导注意力的权重计算.然后,基于获取的注意力权重构建自适应加权的特征变量作为回归层的输入.通过这种策略,可以显著降低由过程噪声引起的模型泛化性能下降.本文中的注意力计算采用加性模型,如式(10)所示,输入信息为经过堆叠的时间卷积模块提取的特征变量,查询信息为提取的历史工况知识.在t时刻,基于工况知识引导的注意力值可由下式计算为

式中:i ∈[1,m];f(t)表示提取的历史工况知识;Qi,Wi,Ui和bi表示式中需要通过学习确定的超参数;gi(t)表示特征向量中的第i个特征在t时刻的注意力值;式(11)用于将注意力值归一化从而保证所有特征的注意力值之和为1;归一化后得到的注意力值被称为历史工况知识引导的注意力,而基于工况知识引导注意力加权的特征向量可以被表示为

3.3 基于工况知识引导注意力时间卷积网络的烧结终点预测框架

通过计算得到基于历史工况知识的注意力值β(t),从而获得预测窗口内的加权特征向量,被用作回归层的输入来建立(t)和之间的非线性映射关系,如式(13)所示,最终得到终点的预测结果.

式中:W和b分别表示回归层的权重和偏置,φ表示激活函数.定义烧结终点的真实测量值为{y(1),y(2),···,y(N)},预测结果为{(1),(2),···,(N)},通过利用Adam优化算法最小化预测值与真实值之间的均方误差(mean square error,MSE)来训练模型,模型的损失函数可表示为

式中N表示训练集中的样本个数.

基于所提的工况知识引导注意力时间卷积网络构建预测模型框架,如图4所示.模型构建的详细步骤如下:

图4 工况知识引导注意力时间卷积网络的烧结终点预测框图Fig.4 Diagram of burning through point prediction based on working condition knowledge guided attention temporal convolutional network

步骤1假设预测时间窗的大小为T,收集预测时间窗口内的历史数据,根据风箱温度数据拟合得到窗口内每个历史采样时刻的烧结终点数据.预测窗口内用作模型输入的过程数据可表示为{x(t-T+1),x(t-T+2),···,x(t)},xt∈Rn,预测目标值为下一时刻的烧结终点位置y(t+1).

步骤2确定模型的超参数,如卷积时间模块的数量和卷积核尺寸,卷积核的尺寸和卷积模块的数量应满足确定的模型记忆长度.

步骤3通过堆叠的时间卷积模块对输入过程数据序列{x(t-T+1),x(t-T+2),···,x(t)}进行特征提取,得到潜变量向量V={v1(t),v2(t),···,vm(t)}.

步骤4为了进一步区分重构特征变量对预测目标的重要程度,计算每个特征在t时刻基于工况知识引导的注意力值β(t),基于注意力值得到加权后的特征向量为

步骤5作为全连接层的输入,最终得到预测结果为(t+1)=φ(W·+b).

4 工业验证

4.1 数据描述与预处理

为了验证所提方法的有效性,本文采用我国华南地区某钢铁集团二号高炉3号烧结厂2021年1月14号至2021年1月20日的生产数据进行仿真实验.根据专家经验和机理分析,对烧结过程中影响烧结终点的过程参数进行筛选,最终确定影响烧结终点的主要参数变量如表2所示.从生产数据库中读取所需的10000组过程参数,过程参数的采样间隔均为1 min.为了改善建模数据质量,需要对数据进行预处理.通过箱线图法剔除过程数据中的异常值,最终得到9000个样本用作训练集,1000个样本用作测试集.

表2 模型输入变量Table 2 The input variables of the proposed model

4.2 模型参数确定

合适的网络参数对于模型的预测性能至关重要.本节挑选了3个重要的超参数进行敏感性实验,它们分别是预测窗口大小、卷积模块个数以及卷积核个数.输入过程序列的长度由滑动窗口的尺寸决定,为了确定合适的滑动窗口大小,通过构建敏感性参数实验分析不同滑动窗口大小对模型预测性能的影响.考虑烧结机长度和速度,候选滑动窗口尺寸为30,35,40,50.表3列出了不同滑动窗口尺寸下预测结果的评价指标,包括相关系(R2)、均方根误差(root mean square error,RMSE)、绝对误差(mean absolute error,MAE)和平均命中率(MSE).结果表明,窗口大小为40时模型的效果最佳.

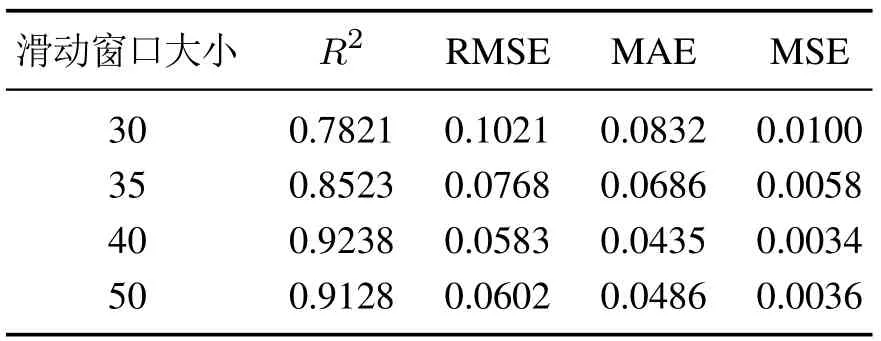
表3 不同的滑动窗口下模型的预测效果对比Table 3 Comparison of prediction performance of models under different sliding windows

此外,浅层的网络结构和较小的卷积核尺寸都会导致模型无法有效捕捉时间序列的长时特征.深度网络结构可以捕获数据的高维特征,但是随着堆叠的时间卷积模块数量增加,模型的性能提升反而受限,且空洞卷积的存在可能会导致模型感受野超过输入序列的长度.如表4所示,当时间卷积模块数达到3时,模型的性能相较之前提升明显,但随着模块数量进一步的增加,模型性能难以获得显著的改进.与此同时,随着卷积模块数量的增加,需要训练的网络参数也随之增加,所需耗费的内存也更多.此外,不同卷积核数量下的预测结果如表5所示,根据表5中列出的预测结果,卷积核个数被设置为30,卷积核大小被设置为4.

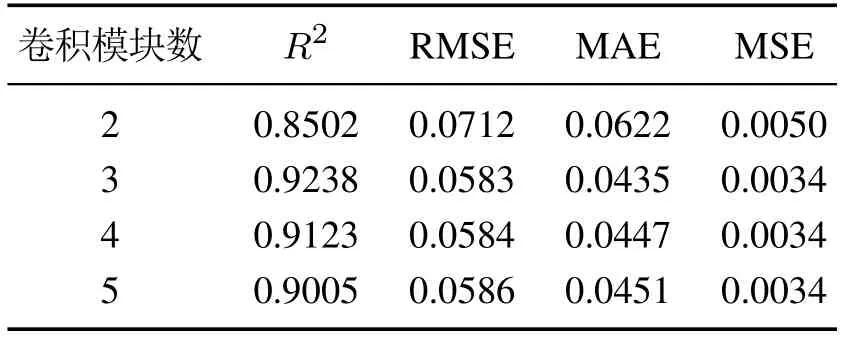
表4 不同卷积模块个数下的预测结果对比Table 4 Comparison of prediction performance of models under different block n umbers

表5 不同卷积核数的预测结果对比Table 5 Comparison of prediction performance of models under different kernel numbers

4.3 结果分析

本文选择了人工神经网络(artificial neural network,ANN)、长短期记忆网络(long short term memory,LSTM)和TCN方法与本文所提方法进行对比实验来验证所提方法在烧结终点预测上的有效性.

表6给出了4种预测方法在预测烧结终点的性能对比结果.从表6可以看出,ANN简单的网络结构无法提取烧结过程数据的复杂非线性特征和动态特性,导致预测性能不佳.LSTM具有历史数据记忆能力,因此,它的性能较ANN有一定的提升.TCN通过利用权重共享的卷积核,减少模型参数的同时获取更多的数据信息,因此TCN的预测性能较LSTM仍有提升.但由于TCN没有充分历史工况知识对预测模型的影响,它的预测性能仍然无法达到最佳.AM-TCN通过将历史数据中包含的工况知识引入模型训练中,从而自适应地确定过程变量表示的状态,可以进一步提高模型性能.因此,所提出AM-TCN方法在4个评价指标上均优于其他方法,具有最好的预测准确率.

表6 各模型的预测性能指标比较Table 6 Comparison of prediction performance indicators for different methods

为了直观地比较AM-TCN 与其他方法的预测性能,图5展示了不同方法在测试集上的预测曲线图.从图5(a)-(d)可以看出ANN和LSTM的预测曲线与真实值曲线均有较大的偏差.虽然TCN的预测线在大多数情况下可以更好地跟踪大测试集上的真实值,但仍然没有拟合的很好.从图5(d)可看出AM-TCN的预测曲线和真实曲线几乎能够重叠成一条线,这也代表了AM-TCN的预测性能最佳.从烧结终点位置变化趋势的跟踪能力上来看,AM-TCN对于烧结终点位置变化趋势的跟踪能力同优于其他3种预测模型.

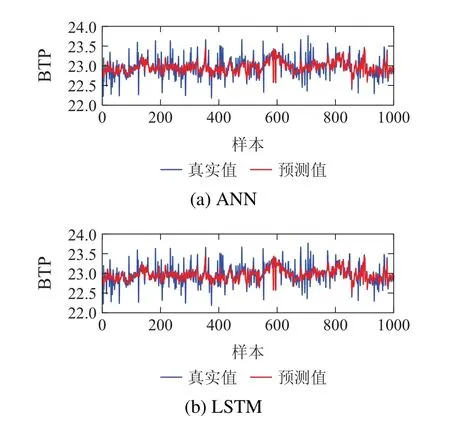
图5 不同模型的烧结终点(BTP)预测曲线Fig.5 BTP prediction curves of different models

5 结论

烧结终点是烧结过程中的关键质量指标.针对烧结过程数据强非线性和动态时变特性问题,本文提出了一种基于工况知识引导注意力时间卷积网络(AMTCN)的烧结终点预测方法.基于实际烧结过程数据的研究结果表明: 1)所提方法相对于传统的静态预测模型,R2,RMSE,MAE和MSE评价指标在预测精度和稳定性均表现更优;2)与常规TCN模型相比,AMTCN在引入了历史工况知识之后,在预测精度和曲线变化趋势上都有了较大程度的提高,可一定程度上满足烧结工业现场对烧结终点指标估计的需求.