盲校小学数学分数教具的具身设计与应用
沈光银 张粤睿 苏凡 王佳圆

【摘要】 数学教具可以表征数学基本知识、基本技能和基本思想。盲校小学数学分数教具的设计可以依据具身设计的原理,将传统视觉通道的教具转化成可借助触觉和运动觉等感觉通道使用的教具,帮助盲生理解并建构分数的多重意义、分数的纵向结构以及分数运算原理,从而培养其分数学习的基本能力。
【关键词】 盲校;小学数学;分数教具;具身设计
【中图分类号】 G761
【作者简介】 沈光银,教授,华南师范大学教育科学学院(广州,510631);张粤睿,硕士研究生,埃塞克斯大学(科尔切斯特,CO43SQ);苏凡、王佳圆,硕士研究生,华南师范大学教育科学学院(广州,510631)。
《盲校义务教育数学课程标准(2016年版)》(以下简称课程标准)明确要求,盲生在分数学习过程中应结合具体情境初步认识分数,理解分数的意义,能读、写分数,比较分数大小,能分别进行简单的分数加、减、乘、除运算及混合运算[1]。受限于视觉障碍,盲生在分数学习中普遍存在分数意义理解因缺乏表象支持而不深刻、分数读写因结构异化而不顺畅、分数运算因计算原理模糊而不透彻等问题。要解决这些分数学习中的问题,就需要教师通过教具帮助盲生理解并建构分数的多重意义、分数的纵向结构以及分数运算原理等基本内容,培养其分数学习的基本能力。
《“十四五”特殊教育发展提升行动计划》强调,要进一步优化完善残疾学生特殊学习用品[2]。课程标准也指出,教师应努力收集、开发制作简便实用的教具和學具,以培养盲生的实践能力[3]。如何设计适合盲生使用的分数教具?具身认知理论认为,个体可以通过具身动作开展逻辑分析、问题解决、意义建构和推理论证等认知活动[4]。基于此,亚伯拉罕森和林德格伦于2014年在《剑桥学习科学手册(第二版)》中提出了具身设计的基本原理[5]。盲校小学数学分数教具的设计可以依据具身设计的原理,将传统视觉通道的教具转化成可借助触觉和运动觉等感觉通道使用的教具。本文结合盲生分数学习中的问题,探析分数教具的设计及其在解决相应问题中的应用。
一、丰富分数意义的多元表征,增强分数概念基本认知
分数具有多重意义,理解分数意义是分数学习的重要基础。分数主要包含部分—整体关系、子集—集合关系、等分除的商、小数、数轴上的点和比值等多种意义,且意义表征的形式各不相同。盲生受视觉障碍的限制,在生活中经历的与分数有关的活动非常有限,且对分数意义的理解缺乏视觉表象的支持。因此,盲生要形成分数的概念,就需要借助具身性的教具强化其对分数意义的理解与建构。
(一)非符号性和符号性教具兼制,增强分数意义表征的逻辑性与确定性
盲生分数学习的首要问题是缺乏有效的关于分数意义的表象。尽管盲生经历过类似切蛋糕、分苹果等生活情境,但实际上并未真正通过触觉感知过这些事物由整体等分为部分的形象化过程。在盲校分数教学中,盲生不单要知道如何用符号表征分数概念的基本形式,更重要的是借助非符号性教具理解分数概念的真正意义。
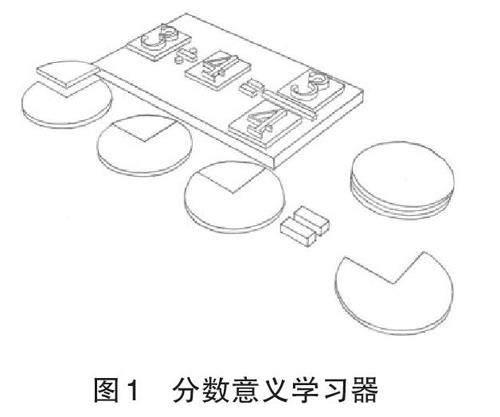
盲校分数教学应首先通过非符号性教具,丰富盲生的分数意义表象。非符号性教具是借助多种图形表征分数基本概念的教学用具,它可以半具体化地把分数概念表征在教具的结构中,从而帮助盲生通过触觉和运动觉感知并理解分数的意义,增强分数意义表征的逻辑性。例如,在分数意义的教学中,为了让盲生理解“分数是等分除的商”这一分数概念,教师设计了“分数意义学习器”(见图1)以解析分数是对整体的等分[6]。盲生通过触摸教具下方区域的分数拼盘,形象地理解“3÷4”就是把3个圆形拼盘的每一个都平均分成4份,其中一份就是3个1/4,进而通过操作活动在教具上方的演算区建构3÷4=3/4的基本原理。
同时,为了帮助盲生掌握分数的基本结构,教师还需要重视符号性分数教具的设计,以增强分数意义表征的确定性。如分数二分之一,可以借助盲文刻印机或3D打印机等制成不同半径的盲文点位
(二)横向性和纵向性教具兼制,增强分数意义表征的深刻性与灵活性
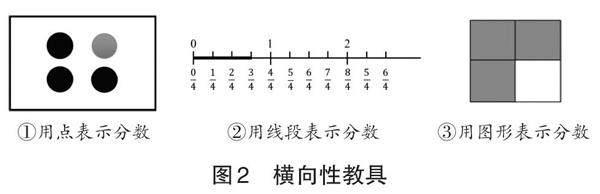
横向性教具是将某一概念或规则用不同的形式加以表现的教具。鉴于分数意义的多重性特征,难以用同一种形式的教具完整表征分数意义。在盲校分数教学中,教师可以借助点、线、面、体等不同形式的凸图设计非符号性教具(见图2),同时将分数概念与数量、长度、面积、体积等结合起来,以增强盲生分数意义理解的深刻性。例如,3/4用点来表示,可以说明子集—集合关系的意义;用线段来表示,可以说明分数单位的概念;用图形来表示,可以说明部分—整体关系的意义。
纵向性教具是将某一概念或规则用同一形式的不同类型加以表现的教具。任何一种分数意义,既可以通过不同的形式进行横向的表征,也可以通过同一形式的不同类型加以表征,从而丰富盲生表征分数意义的具体表象,增强分数意义理解的灵活性。例如,为了让盲生理解并建构1/2的意义,教师可以分别用面积二等分的正方形、长方形、圆形及三角形等图形的不同类型凸图加以演示(见图3),从而增强盲生表征分数意义的灵活性。
二、解构分数运算的基本原理,掌握分数运算基本方法
任何一种运算都应该从算理和算法两个角度进行解析。若盲校小学数学分数运算的教学囿于算法,在形象化过程中缺少表象操作的支持,则会导致在实际教学中偏重运算方法的传授,而忽视甚至省略运算原理的解析。具身设计的分数教具,不仅可以帮助盲生真实感受运算的基本逻辑,而且可以形象地呈现运算的逻辑顺序,有效解决算理与算法脱节问题。
(一)设计表征原理的教具,建构分数计算原理
算理即计算原理,是借助数学概念、定律和性质等,以语义分析的形式说明算式“为什么这样算”的客观规律。例如,类似“2/8+1/8”这种同分母分数的加法,其计算原理以分数概念为起点,即它们的分数单位都是1/8,表示的是2个1/8加1个1/8,合起来是3个1/8,所以2/8+1/8=3/8。分数教学实验研究发现,教师提供中间层次的操作性工具,有利于学生发展分数概念,并为构建运算规律的表象奠定基础[8]。由于视觉通道受阻,盲生在生活中较少产生有关分数概念的常识性感知,且这种具体性的感知与数学运算之间难以有效联结。
为了帮助盲生理解分数运算原理,教师可以设计表象操作性教具,以帮助盲生建构具体生活经验与数学运算之间的联系。这种表象操作性教具是一种半具体化的分数教学用具,它所体现的不再是基于分蛋糕、切苹果这种具体性的分数概念上的计算,而是将日常生活中的分数及其运算抽象成半具体化的、有关分数单位的表象,并基于这种表象建构运算原理。例如,在教学“2/8+1/8”的计算原理时,教师使用“分数计算原理演示器”(见图4),一方面帮助盲生建构“1/8”的分数概念(即把单位1平均分成8份,其中的一份就叫做1/8),另一方面帮助盲生建立分数概念与同分母分数加法运算之间的关系。教师可以引导盲生点数分数计算原理演示器的拼板来理解分数的单位,并通过重叠不同分数单位的拼板来比较分数的大小,进而通过触觉和运动觉来理解“2/8+1/8”就是2块拼板加1块拼板(即2个1/8加1个1/8),在教具的使用中理解并掌握分数运算的基本原理。
(二)设计表征逻辑顺序的教具,解析分数计算方法
算法即計算方法,是依据计算原理,以句法规则的形式规定一类算式“怎么计算”的基本程序或逻辑顺序。例如,同分母分数加减法运算方法是“分母不变,分子相加减”。由于盲文书写结构的异化,盲生难以借助横向的盲文书写顺序辅助分数运算。同时,由于盲文书写需要将盲文纸夹在盲文写字板的面板和底板之间,书写后的盲文无法即写即摸,同样失去了像明眼文一样辅助分数运算的功能。因此,盲生分数运算的学习只能依赖脑海中的逻辑推理及对运算过程的记忆,这样容易造成运算逻辑不明晰、运算过程模糊等问题。
在分数运算方法教学中,教师可以运用具身设计的原理,从盲生的触觉和运动觉等优势通道出发,将分数运算的教具设计成表征计算逻辑顺序的操作性教具,从而帮助盲生将实际的操作活动直接建构成分数运算的方法与过程。例如,在教学分数乘法分配律时,教师设计“分数乘法分配律运算器”(见图5),将分数乘法分配律的基本运算程序表征在实际的操作活动中,一方面有助于盲生通过操作活动理解分数乘法分配律的基本原理,另一方面有助于盲生直接利用该教具进行相关的运算。
三、整合分数运算原理与方法,提升分数运算基本能力
算理为计算提供了正确的思维方式,保证的是计算过程的科学性与合理性;算法为计算提供了具体的操作程序,保证的是计算过程的正确性与快捷性。算理是算法的逻辑依据,而算法则是算理的计算形式,两者相辅相成,密不可分。因此,数学运算教学应算理和算法并重,帮助盲生避免运算原理与方法脱节,陷入只知道怎么计算,而不知道为什么这样计算的困境。
(一)设计整合运算原理与方法的教具,发展分数运算思维
在盲校小学分数计算教学中,教师可以设计运算原理与方法相整合的教具,利用表征运算原理的部分帮助盲生理解计算的思维方式,利用表征运算方法的部分帮助盲生理解计算的逻辑过程。例如,在教学类似“2/8+1/8”的同分母分数的加法时,教师设计“同分母分数加法的整合性教具”(见图6),利用教具上半部分的分数拼板帮助盲生理解同分母分数加法的原理,认清其本质是分数单位相同的分数相加,即数分数单位的份数。接着,盲生根据理解的运算原理,利用教具下半部分的演算区域表征同分母分数加法的运算逻辑,即分数单位同是1/8的两个分数相加,分母8不变,分子1+2=3,所以2/8+1/8=3/8。
(二)设计整合运算内容与过程的教具,提升分数运算能力
盲校小学数学分数运算部分要求盲生掌握分数加法与减法、通分与约分、乘法与除法等学习内容及其运算过程。由于分数运算的常规教学是单纯的逻辑推理和演算,盲生不仅会因为认知资源的大量消耗而感到疲劳,更重要的是光凭记忆推演容易导致运算错误。为了更好地帮助盲生学习分数的各种运算,教师需要运用具身设计的原理开发各种相关的运算工具,如同分母分数加法演算器、同分母分数减法演算器、异分母分数加法演算器、异分母分数减法演算器等。这显然会给教师的教学工作带来很重的负担,且不利于盲生建构分数各运算内容之间的联系。
在分数运算教具的设计中,教师可以将某些运算教具整合在一起,以帮助盲生建构相应的运算体系。例如,教师设计“分数演算器”(见图7),利用传统算盘的原理将分子用算珠表征在上半部分,将分母表征在下半部分,一方面还原了分数的纵向结构,另一方面便于推演各种分数的运算过程。在进行分数加减法演算时,盲生在第一、第二列拨出算式中的两个分数,在第三列拨出相应的结果;在进行分数通分和约分时,在分数演算器任意一列的上下凹槽中分别拨出相应的分子分母,再根据通分和约分的规则,在该列进行演算。
分数概念与盲生日常生活的弱关联性、盲文分数结构的异化性、盲文书写对分数运算的非辅助性等问题导致了盲校小学数学分数教学中的各种困难。究其本质,盲生与分数基本知识和基本技能等相关的抽象逻辑思维的发展缺少了日常生活经验及视觉表象的支撑。盲校小学数学分数教具的具身设计有利于将视觉性的数学教具转化成盲生可通过触觉和运动觉通道使用的教具,从而为分数认识与分数运算的学习提供保障。
【参考文献】
[1][3]中华人民共和国教育部.盲校义务教育数学课程标准(2016年版)[S].北京:人民教育出版社,2018:10-20,69.
[2]中华人民共和国教育部.国务院办公厅关于转发教育部等部门“十四五”特殊教育发展提升行动计划的通知[EB/OL].(2022-01-25)[2024-02-21].http://www.moe.gov.cn/jyb_xxgk/moe_1777/moe_1778/202201/t20220125_596312.html.
[4]Thompson E. Mind in life:biology,phenomenology,and the sciences of mind[M].Boston:Harvard Unive-rsity Press,2010.
[5]Abrahamson D,Lindgren R.Embodiment and embodied design[M]//Sawyer R K.The cambridge handbook of the learning sciences.Cambridge:Cambridge University Press,2014:358-376.
[6]史宁中.基本概念与运算法则[M].北京:高等教育出版社,2019:14.
[7]沈光银.手语在小学中低年级数学教学中的应用[J].网络科技时代,2008(5):95-96.
[8]Behr M J,Harel G,Post T,et al.Rational number,ratio,and proportion[M]//Grouws D A.Handbook of research on mathematics teaching and learning.New York:Macmillan,2006:296-333.
(责任编辑:黄春露)
【基金项目】 本文为国家社会科学基金“十四五”规划2023年度教育学一般课题“盲生与明眼生数感特征的对比及干预研究”(BBA230110)的阶段性研究成果。

