基于单类支持向量机的组合导航容错算法

孙传波, 王 虹, 杨 然, 余国才

(南京理工大学,南京 210000)

0 引言

随着科学技术的不断发展,逐渐成熟的组合导航定位技术在众多领域得到了广泛的应用。不断提高整体导航系统的精度和性能,是组合导航技术发展的重要目标。以SINS/GNSS/BA组合导航系统为例,当GNSS系统受到外部干扰输出异常数据,经过时间更新和数据融合后,整个系统的精度都会受到影响,因此对组合导航系统进行故障检测和判断的重要性不言而喻。

目前较为主流的故障检测方法包括基于解析模型的检测方法、基于小波变换的检测方法和基于神经网络的检测方法。卡方检测法属于典型的基于解析模型的检测方法,文献[1]采用卡方检测法实时判决测量值的有效性,进行故障隔离,但是实际应用中很难获取准确、实时的系统模型和量测模型;文献[2]基于小波模极大值原理设计检测算法,提高了系统的可靠性,但在大尺度条件下可能出现延迟;文献[3]将BP神经网络与组合导航系统结合,提出了新型自适应滤波算法,但是神经网络的在线训练会影响系统工作的实时性;文献[4]使用主元分析法对异常点进行检测,但是对原始数据要求高并难以处理非线性问题。以上常用的故障检测方法都有着各自的局限性[5],在捷联惯导应用背景下,本文以多源组合导航系统为平台,对导航容错算法进行研究,采用基于单类支持向量机(One-Class Support Vector Machine,OCSVM)的容错算法,对系统故障的敏感性更高,处理非线性问题效果更好,提高了组合导航系统的稳定性。

1 多源信息容错组合导航系统

在组合导航系统中,滤波结构对系统的输出结果有很大影响。融合重置式联邦滤波器不仅可以消除子滤波器的相关性,还可以提高系统局部和整体的精度,是如今组合导航的常用结构,但是在子系统发生故障时,容易污染其他子滤波器和主滤波器,容错性较差,因此需要加入故障检测模块[6]。

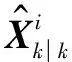
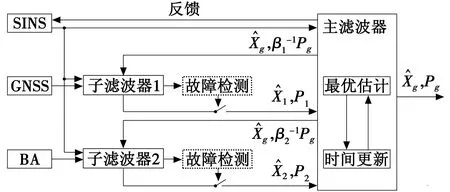
图1 多源信息容错组合导航系统结构图Fig.1 Structure of multi-source information fault-tolerant integrated navigation system

2 基于单类支持向量机的故障检测算法

SVM[7]是一种如今应用较为广泛的机器学习方法,与传统的人工神经网络相比,该方法对非线性、高维数的分类问题的适用性更强[8]。在单类分类问题中使用支持向量机方法称为单类支持向量机(OCSVM)[9]。

2.1 OCSVM基本理论及数学模型

OCSVM的核心思想是通过非线性映射将原始空间内的单类非线性样本组投影到高维特征空间,然后利用超平面将正类样本与原点(唯一负类点)以最大距离分开。其分类原理[10]如图2所示,其中,⊕为正类样本,⊖为负类样本,d为原点与超平面的最大距离。

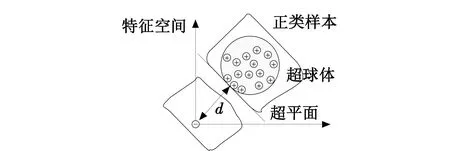
图2 OCSVM分类原理Fig.2 Principle of OCSVM classification

在超平面法[11]中,寻求超平面需解决下述优化问题

(1)

s.t. 〈w,φ(xi)〉≥ρ-ξi,ξi≥0,i=1,2,…,l

式中:ρ∈R,为超平面的截距;w为平面法向量;l为训练集数量;v∈(0,1),为控制参数;ξi为松弛因子;φ(xi)为空间映射。其对偶形式为最小化目标函数

(2)

式中:α=[α1,α2,…,αl]T,为优化权值向量;K为核函数;eT用来求优化权值向量的和。

假设支持向量的集合为I,对应的xi为支持向量,g为新样本,可得超平面的函数形式为

(3)

式中,x为高维向量。对于测试集,若f(x)≥0,则测试点为正常点,反之则为异常点。

2.2 基于OCSVM的故障检测

组合导航中需要对子系统进行故障检测[12],首先使用正常数据对OCSVM进行训练,然后令其对异常数据实现检测功能并加以隔离。此时,为了提高建模效率和系统准确性,需要对原始数据进行预处理。

2.2.1 相空间重构

导航信号为时间序列信号,不符合多维特性,为使其满足支持向量机样本特性,需要对其进行相位重构[13]。

根据Takens嵌入原理,使用延迟法来重构混沌吸引子的相空间,在一定条件下,可以任选时延τ,只要相空间维数m(通常为2k+1)足够大,就可以刻画出该尺度层次上的k维混沌吸引子。最后通过考察时延τ,即可得到一个新的多维坐标[14]。假设系统一定时间内测得的导航数据时间序列为x(t),t=1,2,…,L,L为数据长度,在时延为τ的情况下,重构m维相空间时的相点为

Xi={x(ti),x(ti+τ),x(ti+2τ),…,x(ti+(m-1)τ)}

(4)

式中,i=1,…,M,M=L-(m-1)τ,为重构相空间向量个数。

2.2.2 向量预选取

支持向量对OCSVM最终形式起着决定性作用,通过精简训练样本,提高寻找支持向量的速度,在一定程度上可以提高故障检测的效率。

如有样本集合D={xi∈Rl|i=1,2,…,N},那么在高维特征空间中,样本集合的中心点以及高维向量x与中心点所形成向量c的夹角为

(5)

式中:N为样本数量;xi为样本点;φ(xi)为空间映射。

由式(5)可知,其夹角越大,此向量越可能成为支持向量[15]。因此对于样本集合D,根据

(6)

计算出每个点对应的si的值,选取值较小的xi构成新的样本集就可以达到精简训练样本的目的。式中,k(xi,xj)为核函数矩阵,xj为样本点。

2.2.3 故障检测算法

为了提高OCSVM模型的准确率,在训练模型之前,采用十折交叉验证法(10-fold-validation),将所有样本分为10等份,其中每一等份轮流作为测试数据,从而求取最优模型参数。核函数选用径向基核函数RBF

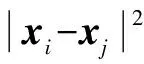
(7)

式中,δ为核宽度,通过十折交叉验证法可以选择检测效果最佳的核宽度和异常点容忍比例。

3 仿真实验

前文已构建了联邦滤波组合导航系统,并加入了故障检测算法,本章将对提出的算法性能进行验证。

3.1 实验方案

首先设定飞行轨迹,基于仿真轨迹产生所需的传感数据,然后将传感数据按比例分为训练样本和测试样本,在测试样本不同时间点加入突变故障和缓变故障,检验算法是否可以将异常点与正常点准确识别,最后将算法应用于组合导航系统进行仿真,通过对比来验证容错系统的有效性。

3.2 轨迹仿真及数据产生

模拟飞行总时间1120 s,IMU数据更新频率为100 Hz,GNSS数据更新频率为10 Hz,以某地为起始点,进行多次转向与爬升之后降落,轨迹图见图3。

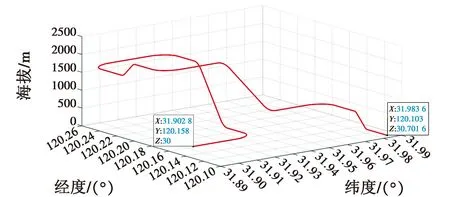
图3 飞行轨迹仿真图Fig.3 Flight path simulation diagram

3.3 正常点与异常点识别

在得到的轨迹数据中选取部分样本点进行训练和测试,若测试样本点中SINS子系统如图4所示出现数据异常,仿真后将得到图5所示的识别结果。

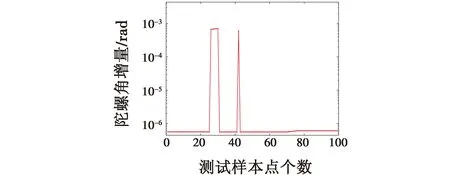
图4 测试点数据时域图Fig.4 Time domain diagram of test point data

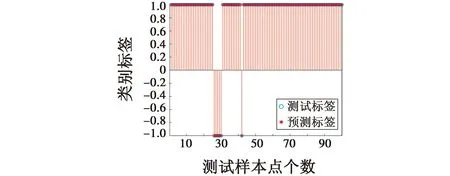
图5 测试集实际与预测标签分类Fig.5 Actual and predictive tag classification in test set

仿真中,利用交叉验证法对样本数据进行多次测试,求取最优nu和gamma参数,以获得最佳的边界,由图5可知,本文算法可以很好地检测出物体运动中的故障数据。

3.4 组合导航容错仿真

为了验证容错算法在实际情况下的可靠性,根据已有GNSS数据,建立GNSS子系统故障检测模型,假设在500 s时GNSS子系统高度数据出现异常,图6(a)～6(c)分别展现了对高度数据不采用故障检测的情况下、加入卡尔曼滤波处理的情况下和加入本容错算法的情况下的误差估计,其中,δL为纬度误差,δλ为经度误差,δH为高度误差,δP为组合导航系统误差。

图6 不同处理方法下组合导航系统误差估计Fig.6 Error estimation of integrated navigation system under different processing methods

表1为不同处理方法下,测得的是在470～570 s时间内的3组高度误差的均方根值。

表1 高度误差均方根值

从图6和表1可以看到,在没有隔离故障数据的情况下,不采用故障检测或采用卡尔曼滤波方法处理数据,即使经过组合导航系统的修正,一定时间内高度上的定位精度仍然受到了很大影响,而隔离故障数据后,高度上的定位精度有了明显提升。因为故障和误差的特性不一样,采用滤波算法只能降低故障值的幅度,很难达到理想效果。

3种处理方法下的组合导航定位效果如图7所示。

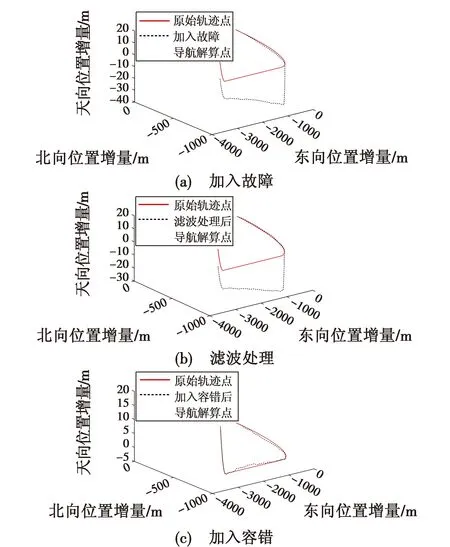
图7 原始轨迹与解算轨迹对比Fig.7 Comparison between the original trajectory and the computed trajectory

结合联邦滤波组合导航系统和3组实验数据对图7进行分析可知:未加入故障检测模块时,一旦子系统出现故障,在无法隔离故障数据的情况下,故障数据被当作正常数据送入主滤波器进行融合,并参与最优估计、时间更新和数据反馈等过程,因此故障数据会污染主滤波器和其他子滤波器,一定时间内组合导航系统的精度会变差,解算轨迹大幅度偏离实际轨迹;当组合导航系统在加入本文所提的容错算法后,故障数据进入主滤波器前,经过训练后的故障检测模块可以快速地将故障值隔离,避免异常数据影响系统精度,解算轨迹与原始轨迹基本吻合,两者位置误差较小,组合导航系统的稳定性和可靠性得到了提升。

4 结束语

本文提出了一种基于单类支持向量机(OCSVM)的组合导航容错算法,并在基于联邦滤波结构的多源组合导航系统上进行仿真分析,验证了该算法的有效性。采用本文算法可在一定程度上提高组合导航系统的稳定性和可靠性。