Dissociation cross sections of ψ(3770),ψ(4040),ψ(4160),and ψ(4415) mesons with nucleons

Ruo-Qing Ding ,Xiao-Ming Xu,∗ and H J Weber

1 Department of Physics,Shanghai University,Baoshan,Shanghai 200444,China

2 Department of Physics,University of Virginia,Charlottesville,VA 22904,United States of America

Abstract We study the dissociation of ψ(3770),ψ(4040),ψ(4160),and ψ(4415)mesons in collision with nucleons,which takes place in high-energy proton-nucleus collisions.The quark interchange between a nucleon and a meson leads to the dissociation of the meson.We consider the reactions:,where R stands for ψ(3770),ψ(4040),ψ(4160),or ψ(4415).A reaction of a neutron and a meson corresponds to a reaction of a proton and the meson by replacing the up quark with the down quark and vice versa.Transition-amplitude formulas are derived from the S-matrix element.Unpolarized cross sections are calculated with the transition amplitudes for scattering in the prior form and in the post form.The cross sections relate to nodes in the radial wave functions of ψ(3770),ψ(4040),ψ(4160),and ψ(4415) mesons.

Keywords: inelastic nucleon-charmonium scattering,quark interchange,relativistic constituent quark potential model

1.Introduction

It is shown in [1–3] that ψ(3770),ψ(4040),ψ(4160),and ψ(4415) mesons are the 13D1,33S1,23D1,and 43S1states of a charm quark and a charm antiquark.The fourmesons have been widely studied ine+e-annihilation that produce hadrons[4–7],ππJ/ψ[8–10],ηJ/ψ[9–12],K+K-J/ψ[10],γχcJ(J=1,2) [10,13],two charmed mesons [14,15],D0D*-π+[16],two charmed strange mesons[17,18],ππhc[19],ωχc2[20],μ+μ-[21],and[22].Electron-positron annihilation produces a virtual photon which splits into a charm quark and a charm antiquark,and this quark-antiquark pair becomes ameson nonperturbatively.Production of the ψ(3770) meson ine+eannihilation was studied in the nonrelativistic quantum chromodynamics (NRQCD) factorization formalism that includes color-singlet and color-octet contributions [23].In [24,25] the conversion of the photon to the ψ(4040) or ψ(4160) meson is indicated by a constant factor.

Au-Au collisions at the Relativistic Heavy Ion Collider(RHIC) and Pb-Pb collisions at the Large Hadron Collider(LHC) produce quark-gluon plasmas.At the critical temperatureTc,the quark-gluon plasma becomes hadronic matter.Since ψ(4040),ψ(4160),and ψ(4415) mesons are dissolved in hadronic matter when the temperature is larger than 0.97Tc,0.95Tc,and 0.87Tc,respectively [26],they can only be produced in hadronic matter.Therefore,the production of ψ(4040),ψ(4160),and ψ(4415) can be taken as probes of hadronic matter that results from the quark-gluon plasma created in ultrarelativistic heavy-ion collisions.In hadronic matter,they are produced in the following reactions:and so on,whereRstands for ψ(4040),ψ(4160),or ψ(4415).Charmed mesons have been well measured in Pb-Pb collisions at the LHC.It is shown in [27] that numbers of ψ(4040),ψ(4160),and ψ(4415) produced in a central Pb-Pb collision at the center-of-mass energy per nucleon-nucleon pair=5.02 TeV are 0.25,0.1,and 0.18,respectively.Therefore,it is interesting to measure ψ(4040),ψ(4160),and ψ(4415)mesons produced in Pb-Pb collisions at the LHC.

Production ofD-wave charmonia in nucleon-nucleon collisions was studied in NRQCD in[28].Production cross sections depend on parton distribution functions,short-distance processes,and nonperturbative matrix elements of four-fermion operators.In proton-nucleus reactions a charmonium produced in a protonnucleon collision further interacts with other nucleons.The nucleon-charmonium collisions may break the charmonium,and thus reduce the charmonium number.Therefore,in the present work we study the dissociation of ψ(3770),ψ(4040),ψ(4160),and ψ(4415) mesons in collisions with nucleons.Since many experiments onpAreactions have been carried out at the RHIC and the LHC,it is interesting to study the dissociation processes.

ψ(3770),ψ(4040),ψ(4160),and ψ(4415) mesons are of special interest because they are easily produced at electronpositron colliders.The mechanism of producing them in protonnucleus reactions is different from the mechanism of producing them in electron-positron collisions.The mesons are influenced by cold nuclear matter due to the dissociation processes and nuclear modification of parton distribution functions.Therefore,it will be interesting to compare the production of the mesons in proton-nucleus reactions with the production in electron-positron collisions in both experiment and theory in future.

This paper is organized as follows.In section 2 we derive formulas of transition amplitudes which are used to calculate unpolarized cross sections for the dissociation ofcc¯ mesons in collisions with nucleons.In section 3 we present numerical cross sections along with relevant discussions.In section 4 we summarize the present work.

2.Formalism

We consider the reactionA+B→C+DwhereAandCrepresent baryons andBandDare mesons.Denoted byEiand,the total energy and the total momentum of the initial(final)baryon and the initial(final)meson,respectively.IfEA(EB,EC,ED)stands for the energy of hadronA(B,C,D),Ei=EA+EBandEf=EC+ED.LetHIbe the interaction potential between two constituents of hadrons in the reactionA(q1q2q3)+→C(q1q2c)+,whereq1,q2,andq3represent light quarks.Since the quark flavors inside baryonAdiffer from the charm flavor inside mesonB,the quark interchange (for example,q3andc) between baryonAand mesonBgives rise to the reaction.TheS-matrix element forA+B→C+Dis

for baryonA,and

for baryonC,whereare the position vectors of quarksq1,q2,q3,andc,respectively.The wave function |A,B〉 of baryonAand mesonBis

and the wave function |C,D〉 of baryonCand mesonDis

in whichVis the volume where every hadron wave function is normalized.is the product of the color wave function,the flavor wave function,the spin wave function,and the space wave function of the three quarks.is the product of the color wave function,the flavor wave function,the spin wave function,and the quark-antiquark relative-motion wave function.

With the wave functions we have

The wave function of baryonAand mesonBis

and the wave function of baryonCand mesonDis

The interaction that governs scattering in the prior form shown in figure 1 is

and the interaction that governs scattering in the post form shown in figure 2 is

whereVabis the potential between constituentsaandb.Letbe the position vector of antiquark.We take the Fourier transform of the potentials and wave functions:

When quarksq1andq2have equal masses,their masses are indicated bym.Let,mc,andstand for theq3,c,andmasses,respectively.From equations (8)–(29) we obtain the transition amplitude for scattering in the prior form,

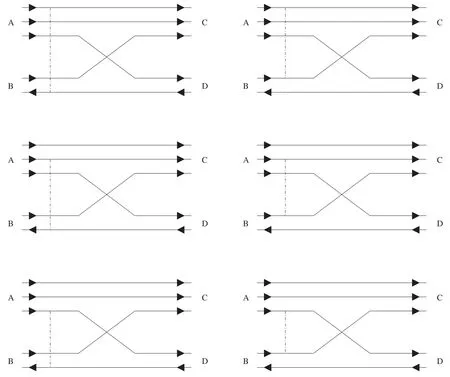
Figure 1. Scattering in the prior form.Solid lines with triangles right(left)represent quarks(antiquarks).Dot-dashed lines indicate interactions.

With the transition amplitudes the unpolarized cross section forA+B→C+Dis

wheresis the Mandelstam variable obtained from the fourmomentaPAandPBof hadronsAandBbys=(PA+PB)2;JA(JB,JC,JD)andJAz(JBz,JCz,JDz)of hadronA(B,C,D)are the total angular momentum and itszcomponent,respectively;θ is the angle betweenwhich are the threedimensional momentum components of baryonsAandCin the center-of-momentum frame of the initial baryon and the initial meson,respectively.We calculate the cross section in the center-of-momentum frame.

3.Numerical cross sections and discussions

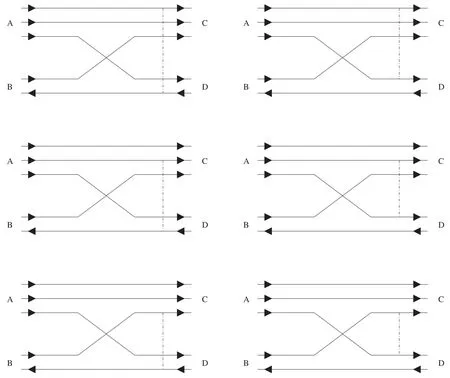
Figure 2. Scattering in the post form.Solid lines with triangles right (left) represent quarks (antiquarks).Dot-dashed lines indicate interactions.

wheredα=0.34 GeV anddβ=0.45.The potential originates from quantum chromodynamics (QCD) [29].The first two terms are the Buchmüller–Tye potential,and the other terms come from one-gluon exchange plus perturbative one-and twoloop corrections [30].

The functionv(x) manifests one-gluon exchange plus perturbative one-and two-loop corrections between constituentsaandb.It increases from 0 to 1 whenxincreases from 0 to the positive infinity.Consequently,the second term is not a color Coulomb potential.

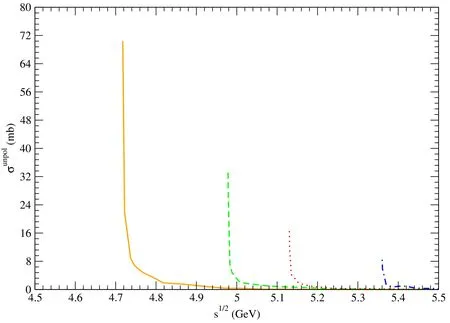
Figure 3. Solid,dashed,dotted,and dot-dashed curves stand for cross sections for pψ(3770)→,pψ(4040)→,pψ(4160)→,and pψ(4415)→,respectively.

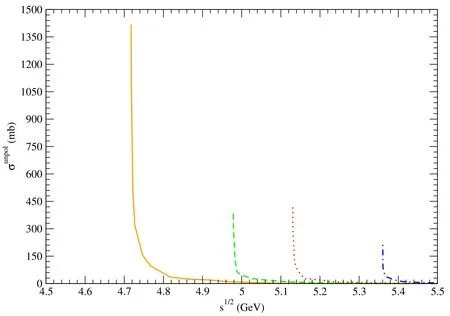
Figure 4. Solid,dashed,dotted,and dot-dashed curves stand for cross sections for pψ(3770)→,pψ(4040)→,pψ(4160)→,and pψ(4415)→,respectively.

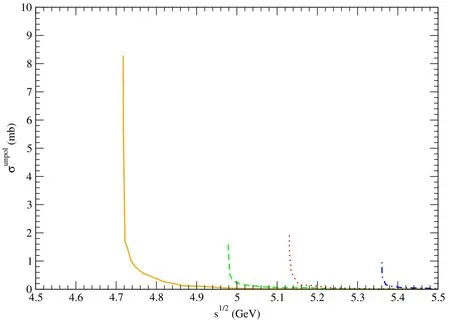
Figure 5. Solid,dashed,dotted,and dot-dashed curves stand for cross sections for pψ(3770)→, pψ(4040)→,pψ(4160)→,and pψ(4415)→,respectively.

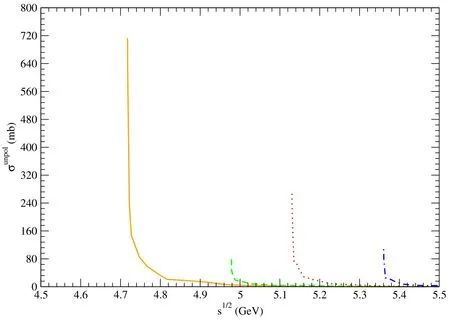
Figure 6. Solid,dashed,dotted,and dot-dashed curves stand for cross sections for pψ(3770)→,pψ(4040)→,pψ(4160)→,and pψ(4415)→,respectively.

The masses of the up quark,the down quark,the strange quark,and the charm quark are 0.32 GeV,0.32 GeV,0.5 GeV,and 1.51 GeV,respectively.Solving the Schrödinger equation withVab,we obtain meson masses that are close to the experimental masses of π,ρ,K,K*,D,D*,Ds,,J/ψ,χc,ψ′,ψ(3770),ψ(4040),ψ(4160),and ψ(4415)mesons listed in[31].The experimental data ofS-waveI=2 elastic phase shifts for ππ scattering [32] are reproduced in the Born approximation.

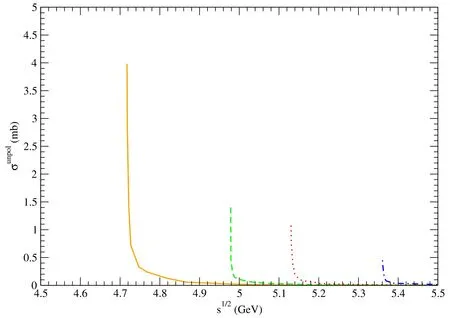
Figure 7. Solid,dashed,dotted,and dot-dashed curves stand for cross sections for pψ(3770)→, pψ(4040)→,pψ(4160)→,and pψ(4415)→,respectively.

Using the mesonic quark-antiquark relative-motion wave functions and the space wave functions of the baryons,we obtain unpolarized cross sections for dissociation of ψ(3770),ψ(4040),ψ(4160),and ψ(4415) mesons in collisions with protons.The cross sections are plotted in figures 3–12,and are parametrized as

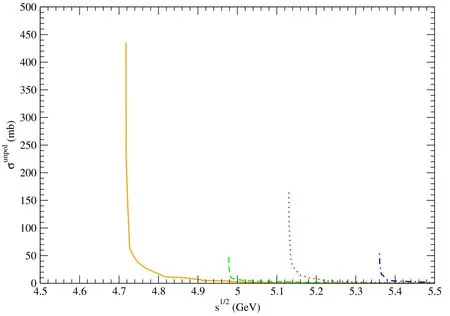
Figure 8. Solid,dashed,dotted,and dot-dashed curves stand for cross sections for pψ(3770)→,pψ(4040)→,pψ(4160)→,and pψ(4415)→,respectively.

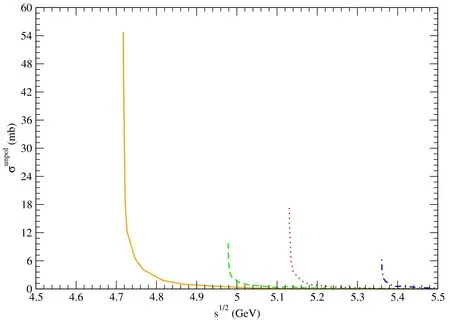
Figure 9. Solid,dashed,dotted,and dot-dashed curves stand for cross sections for pψ(3770)→,pψ(4040)→,pψ(4160)→,and pψ(4415)→,respectively.

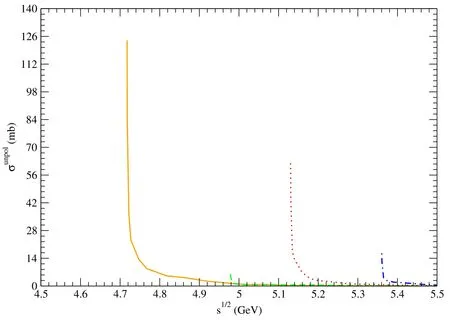
Figure 10. Solid,dashed,dotted,and dot-dashed curves stand for cross sections for pψ(3770)→,pψ(4040)→,pψ(4160)→,and pψ(4415)→,respectively.

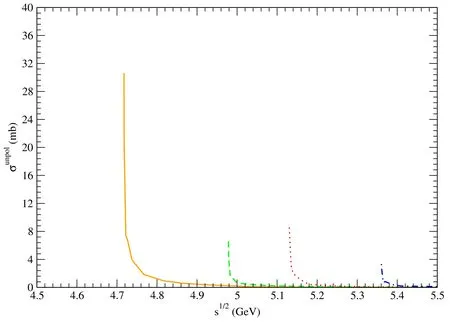
Figure 11. Solid,dashed,dotted,and dot-dashed curves stand for cross sections for pψ(3770)→,pψ(4040)→,pψ(4160)→,and pψ(4415)→,respectively.

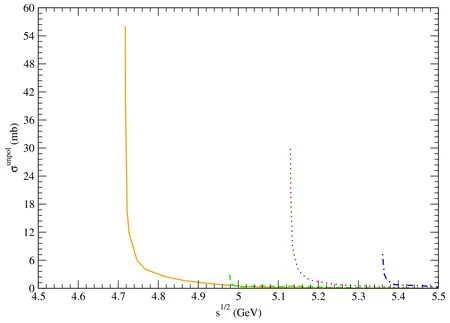
Figure 12. Solid,dashed,dotted,and dot-dashed curves stand for cross sections for pψ(3770)→,pψ(4040)→,pψ(4160)→,and pψ(4415)→,respectively.

The measured proton mass has a very small uncertainty,and the uncertainty is neglected here.The measured masses of charmed baryons have uncertainties[31],for example,themass has an error of 0.14 MeV.The measured mass of every charmed baryon has a maximum and a minimum,for example,themass has the maximum mass 2286.60 MeV and the minimum mass 2286.32 MeV.Fits to the maximum experimental masses of,andbaryons give=0.43 GeV and

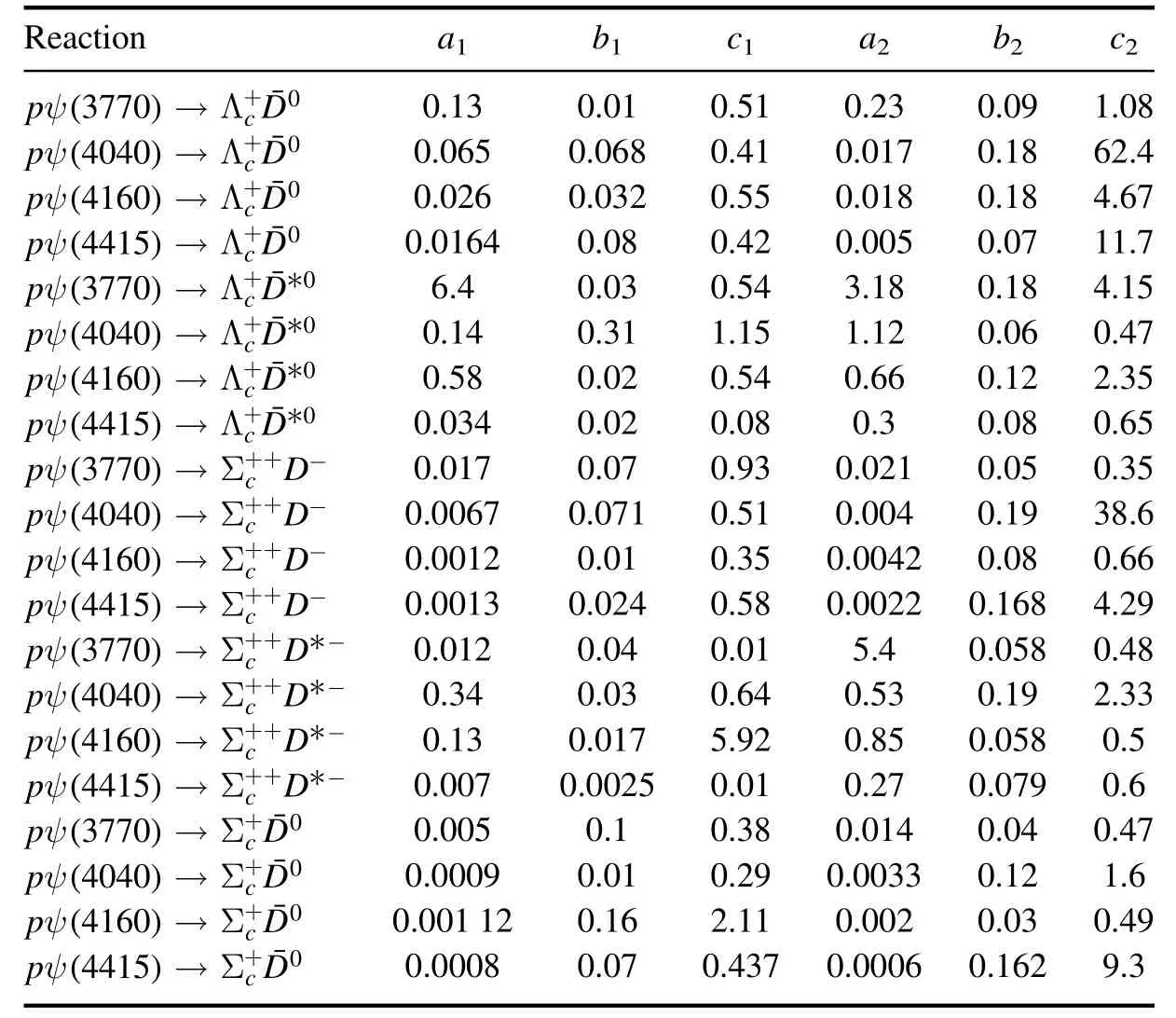
Table 1. Values of the parameters. a1 and a2 are in units of millibarns; b1 and b2 are in units of GeV; c1 and c2 are dimensionless.

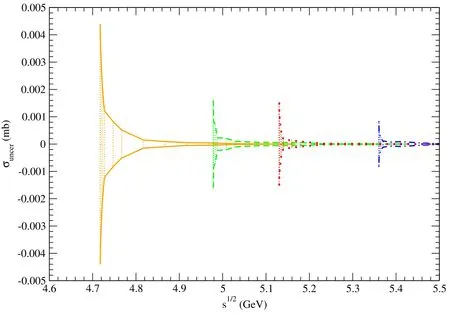
Figure 13.The error band between the two solid (dashed,dotted,and dot-dashed) curves indicate uncertainties of the unpolarized cross sections for pψ(3770)→.

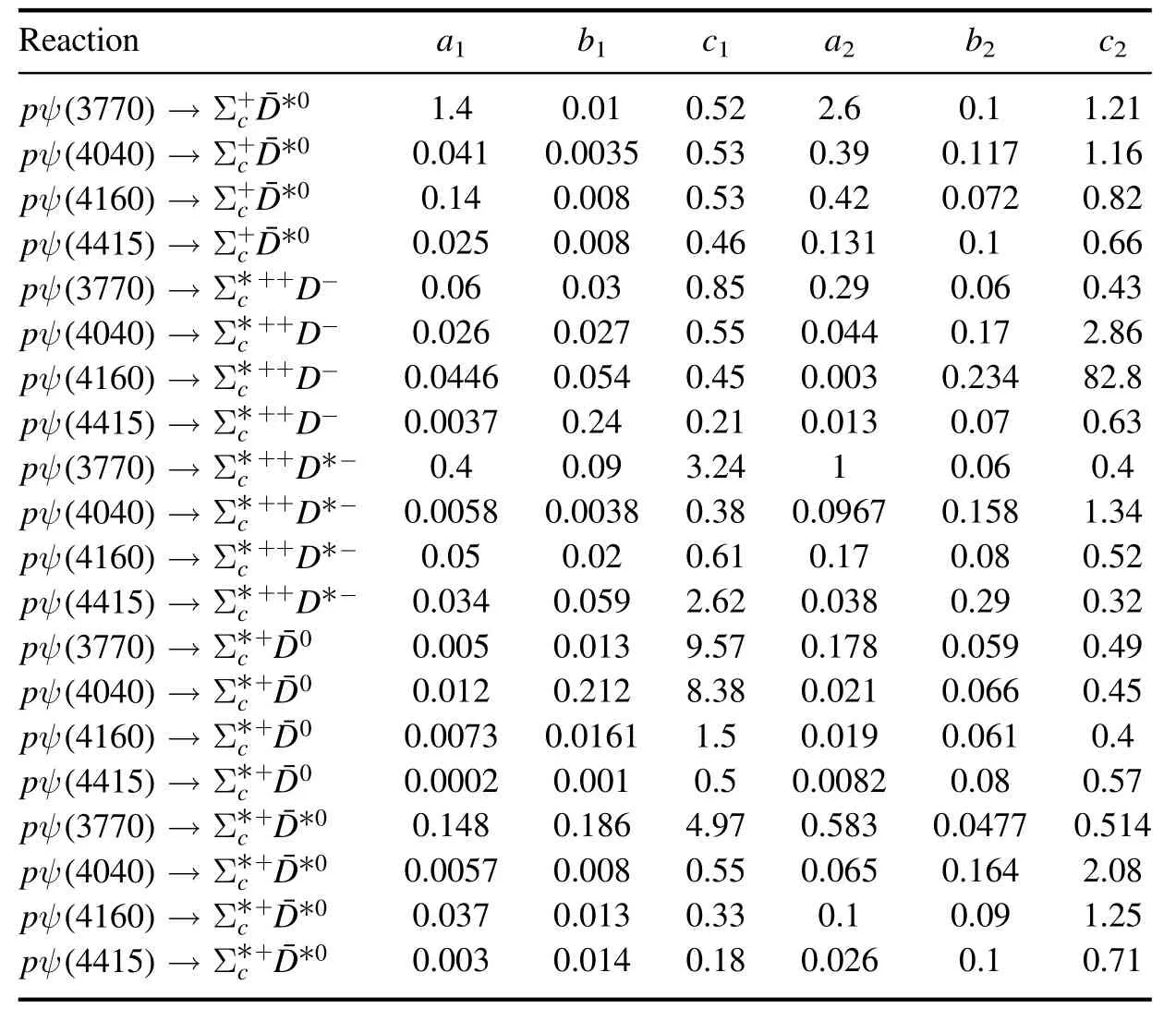
Table 2. The same as table 1,but for twenty other reactions.

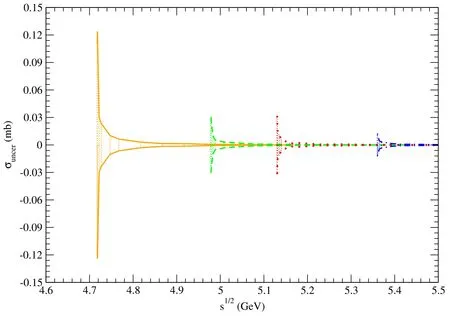
Figure 14. The error band between the two solid (dashed,dotted,and dot-dashed) curves indicate uncertainties of the unpolarized cross sections for pψ(3770)→.

Figure 15. The error band between the two solid (dashed,dotted,and dot-dashed) curves indicate uncertainties of the unpolarized cross sections for pψ(3770)→.

Figure 16. The error band between the two solid (dashed,dotted,and dot-dashed) curves indicate uncertainties of the unpolarized cross sections for pψ(3770)→.

Using these values of αρand,we obtain unpolarized cross sections which are denoted as.The differences betweenand σunpolare plotted as the upper solid,dashed,dotted,and dot-dashed curves in figures 13–22.In every figure the orange (green,red,blue) band between the lower and upper solid (dashed,dotted,dot-dashed) curves show uncertainties of the unpolarized cross sections,which are labeled as σuncerand are caused by the uncertainties of the αρvalue.However,the cross section uncertainties are too small to be shown if the bands are attached to those curves in figures 3–12.The cross section uncertainties are small because of the small uncertainties of the αρvalues,which correspond to errors of measurement of the baryon masses.

Figure 17. The error band between the two solid (dashed,dotted,and dot-dashed) curves indicate uncertainties of the unpolarized cross sections for pψ(3770)→.

Figure 18. The error band between the two solid (dashed,dotted,and dot-dashed) curves indicate uncertainties of the unpolarized cross sections for pψ(3770)→.

In [1–3],ψ(3770),ψ(4040),ψ(4160),and ψ(4415)mesons are identified with the 13D1,33S1,23D1,and 43S1states of a charm quark and a charm antiquark.This identification is also true with the potential given in equation (33),and we then study inelastic scattering of a nucleon by the fourmesons in the present work.However,we note that the quantum states of ψ(3770) and ψ(4415)mesons are open to debate.The 13D1state of the ψ(3770)meson is suggested to be mixed with the 23S1state in [35],and may contain a four-quark component with the up-and down-quarks and antiquarks in [36].The ψ(4415)meson may be a 53S1state given in the screened potential model [37],a 33D1state obtained with a quark potential derived from a Lagrangian with chiral symmetry breaking in[38],or ahybrid recognized in lattice calculations of meson masses[39],from the nonrelativistic reduction of the QCD Hamiltonian in the Coulomb gauge [40],and in the flux-tube model [41].

Figure 19. The error band between the two solid (dashed,dotted,and dot-dashed) curves indicate uncertainties of the unpolarized cross sections for pψ(3770)→(pψ(4040)→,pψ(4160)→,and pψ(4415)→).

Figure 20. The error band between the two solid (dashed,dotted,and dot-dashed) curves indicate uncertainties of the unpolarized cross sections for pψ(3770)→(pψ(4040)→,pψ(4160)→,and pψ(4415)→).

4.Summary

Figure 21. The error band between the two solid (dashed,dotted,and dot-dashed) curves indicate uncertainties of the unpolarized cross sections for pψ(3770)→(pψ(4040)→,pψ(4160)→,and pψ(4415)→).

Figure 22. The error band between the two solid (dashed,dotted,and dot-dashed) curves indicate uncertainties of the unpolarized cross sections for pψ(3770)→(pψ(4040)→,pψ(4160)→,and pψ(4415)→).

Acknowledgments

This work was supported by the project STRONG-2020 of the European Center for Theoretical Studies in Nuclear Physics and Related Areas.