Phase structures and critical behavior of rational non-linear electrodynamics Anti de Sitter black holes in Rastall gravity

Yassine Sekhmani ,Dhruba Jyoti Gogoi,Ratbay Myrzakulov and Javlon Rayimbaev

1 Ratbay Myrzakulov Eurasian International Centre for Theoretical Physics,Astana 010009,Kazakhstan

2 L.N.Gumilyov Eurasian National University,Astana 010008,Kazakhstan

3 Department of Physics,Moran College,Moranhat,Charaideo 785670,Assam,India

4 Theoretical Physics Division,Centre for Atmospheric Studies,Dibrugarh University,Dibrugarh 786004,Assam,India

5 New Uzbekistan University,Movarounnahr Str.1,Tashkent 100000,Uzbekistan

6 University of Tashkent for Applied Sciences,Gavhar Str.1,Tashkent 100149,Uzbekistan

7 National University of Uzbekistan,Tashkent 100174,Uzbekistan

Abstract This research paper presents a black hole solution with a rational nonlinear electrodynamics source within the Rastall gravity framework.The paper analyzes the thermodynamic properties of the solution in normal phase space and explores its critical behavior.The phase structure is examined using the extended first law of thermodynamics,with the cosmological constant Λ serving as pressure P.The isotherms exhibit van der Waals behavior at small values of horizon r+.The paper also investigates the Gibbs free energy behavior and finds two critical points with two pressures where the re-entrant phase transition occurs and disappears.We also explore the prevalent microstructure of black holes in Ruppeiner geometry,uncovering significant deviations in the nature of particle interactions from conventional practice.Moreover,the thermodynamic geometry is analyzed using the Ruppeiner formalism,with the normalized Ricci scalar indicating possible point-phase transitions of the heat capacity,and the normalized extrinsic curvature having the same sign as the normalized Ricci scalar.The three-phase transitions of the heat capacity are those that we find for the normalized Ruppeiner curvatures.Thus,there is an absolute correspondence.

Keywords: Rastall gravity,black hole,Phase structures

1.Introduction

The theory of general relativity(GR)is the best-known initial theory of the geometric framework for gravity [1].Within each of the predictions,the presence of black holes and gravitational waves (GWs) is the most enthralling prediction of GR.About a century after its prediction,the feasibility of GR gained traction with direct observation of GWs by the twin detectors of the Laser Interferometer Gravitational Wave Observatory (LIGO) [2].These ground-based LIGO,Variability of Solar Irradiance,and Gravity Oscillations (Virgo)detector systems anticipated the binary black hole systems,which served as credible proof of the validity of GR.Furthermore,the direct detection of GWs opened up a new pathway for testing or constraining alternative or modified gravity theories,as well as GR.In weak-field regimes as well as moderately relativistic regimes,GR is shown to pass several physical tests,such as solar system tests [3] and constraints from binary pulsars[4,5].Furthermore,the discovery of GWs by LIGO and Virgo detectors has confirmed their validity in the extremely relativistic strong gravity regime associated with binary black holes.Hence,these GWs have significantly altered our picture of the cosmos.Recent studies show that the properties of GWs might vary based on the type of modified gravity.For example,in metric f(R)gravity,GWs possess three polarization modes:tensor plus and cross or GR modes,and scalar polarization mode.The tensor plus and cross modes propagate through spacetime at the speed of light and are,in general,transverse,traceless,and massless in nature.The scalar polarization mode,however,is a hybrid of the massless breathing mode and the massive longitudinal mode [6–8].The massless breathing mode is transverse in nature but not traceless.Consequently,the investigation of the properties of black holes (which are regarded as the cleanest objects in the Universe) and other compact stars like neutron stars (potential candidates for the generation of GWs) in the modified gravity regime was prompted by these new and fascinating characteristics of GWs in different modified theories of gravity.

Thef(R) theories are commonly considered as one of the simplest extensions of GR so far.Apart fromf(R),another simple extension with violation of energy–momentum conservation is Rastall gravity,which was introduced in 1972 by Rastall [9].This idea attracted little attention of the scientific community when it was first proposed.But recently,it has attracted a large number of researchers due to its simple field equations and unique black hole solutions.The original conservation law is modified in this theory of gravity by setting the covariant divergence of the energy–momentum tensor proportional to the covariant divergence of the Ricci curvature scalar.Regardless,by merely setting the background curvature to zero,the typical conservation rule of GR can simply be obtained.It should also be noted that,in the absence of any matter source,the Rastall gravity is equivalent to the GR.This modified gravity has recently been employed in a diversity of contexts.Many contributors [10,11],have already studied black holes and neutron stars within the framework of this theory of gravity.Static and spherically symmetric solutions for neutron stars are discussed in [10].In that theory too,the work carried out on the solutions of black holes is given in[11].A study on the possible solutions of black holes surrounded by ideal fluids is presented in another publication in the same year[12].Quasinormal modes are studied in[68]for black holes surrounded by quintessence fields in Rastall gravity.This work has revealed the appropriate quasi-normal modes as a function of the parameters of the Rastall gravity model.In this work,two cases are taken into consideration: one refers to κ λ<0,which exhibit faster damping for gravitational,electromagnetic,and massless scalar fields.The second deals with κ λ>0,from which slower damping is present for gravitational,electromagnetic,and massless scalar fields.In the former scenario,the actual frequencies of the quasi-normal modes were found to be higher than in the GR.By contrast,in the second scenario,they were lower.Also,they deduced that the changes in the frequencies of the real and imaginary quasi-normal modes with κλ are comparable for different values oflandn[13–15].In parallel,many attempts have been made to reveal the phase structure of black holes within the framework of Rastall gravity.In particular,according to [16],a charged Anti de Sitter (AdS) black hole surrounded by a perfect fluid is constructed within Rastall gravity.Indeed,the matter sector can be characterized in terms of multiple probable kinds of rational nonlinear electrodynamics sources,such as dust and radiation,or exotic matter,like a quintessence,ΛCDM type,and phantom fields.For a choice of a phantom field,the charged AdS black hole shows what is called a reentrant phase transition(RPT)when some of its parameter spaces satisfy certain constraints.

The performance of the critical study for revealing phase transitions is roughly a major concreting step for black hole thermodynamics.Hawking and Page demonstrated from their contributory work that there is a range of first-order black hole phase transitions between large,stable black holes and thermal radiation in anti-de Sitter space [17].This work initiated the possibility of investigating the thermodynamic phase transition in black holes.An emerging reason is constructed within the anti-de Sitter/conformal field theory theories (AdS/CFT)[18–20],implying at the level of the Hawking–Page phase transition that this transition can be interpreted as the gravitational dual of the confinement/deconfinement phase transition of gauge fields[21].Then,the AdS/CFT duality stretched out onto the charged and rotating AdS black holes [22–24].

Recently,the pioneering of AdS black hole thermodynamics has been widely regarded as a new version of phase space,or extended phase space,after considering the cosmological constant as thermodynamic pressure [25–27,29,31].Basically,this consideration led to some thermodynamic phase transition results for a class of ordinary black holes.In AdS spaces,the charged black hole reveals van der Waals-like behavior [22,23].The critical study for the charged black hole,or the Reissner–Nordström–AdS (RNAdS),undergoes a first-order phase transition,revealing a similarity with the van der Waals liquid–gas phase transition.The critical behavior of the black hole along theP–Vdiagram is performed in extended phase space by Kubiznak and Mann[32,33],which reinforced the relation between charged AdS black holes and liquid–gas van der Waals systems [27–30,32,33].Meanwhile,the emergence of thermodynamic geometry inspired by Ruppeiner formalisms is an endeavor to draw,phenomenologically or qualitatively,insights into the microscopic interactions of a set system from the axioms of thermodynamics.The key idea is that,in ordinary thermodynamic systems,the curvature of Ruppeiner metrics is linked to the nature of the interactions among the underlying particles.Particularly for systems where the microstructures interact in an attractive pattern,the curvature scalar is assigned a negative sign,versus a positive one,for mostly repulsive forces.Further,the metric is flat for systems with no interaction,like the ideal gas.This approach has been successfully demonstrated for a broad variety of statistical and physical models.Excitingly,new studies have highlighted that this is viable for black holes as well,thereby supplying an empirical tool for deriving the microstructure of black holes from macroscopic insight [34–41],notwithstanding the absence of a quantum theory of gravitation.

The latest activities in which the physical aspect is thermodynamics or whether (optics,quasi-normal modes,…)in the essence of a black hole spacetime within the context of modified gravity models are now constituting a large amount of interest in theoretical physics.The purpose of examining such an extension of GR is considered a step toward reinforcing the general theory of relativity and establishing solid approaches to it.Nowadays,most works are taken in the essence of modifying gravity through the study of phase transitions[42–49],quasi-normal modes[50–56],and shadow behavior for black hole spacetime [57–62].

The type leading to the existence of such black holes with regular spacetime is related as a consequence of curvature singularities,implying the non-singular behavior of spacetime structure.To avoid the singularity,Gliner [63]and Sakarov [64] modeled a situation in which the matter source behaves like a de Sitter core at the center of spacetime with the state equationp=-ρ.As the approach to the singularity problem was clearly understood,Bardeen invented a way to find the first non-singular solution of Einstein’s equations,namely,the Bardeen regular black hole [65].The solution is nowhere singular and therefore regular in all spacetime,involving a de Sitter center,according to suggestions in Sakharov’s work,as well as satisfying the weak energy conditions.The possible classification of the famous nonlinear electrodynamic source is followed up with the Bardeen,Hayward,and Ayon-Beato–Garcia kinds of matter sources and,thereby,in GR,their possible solutions to the black hole are appropriately examined [66,67].

The outline of this work is as follows: the first section consists of building a black hole solution in Rastall gravity with a rational nonlinear electrodynamics source.The second section is devoted to determining all the thermodynamic quantities in the normal phase space,such as temperature,entropy,heat capacity,and Gibbs free energy.Next,the third section is the part that takes care to study,in extended phase space,the phase structure along theP–Vcriticality and shows the behavior of the Gibbs free energy.The last section deals with the investigation of thermodynamic geometry.Finally,we summarize our work with a conclusion.

2.Rastall gravity

This section’s goal is to obtain a solution while taking into account the physical background of the gravity sector as well as the matter source.To begin working toward this goal,the computation includes,in a way,two blocks regarding the model: the Rastall field equations and the matter field equations.We begin by looking at the Rastall gravity sector.

In this interesting modification of GR,the covariant conservation condition=0was changed to a more generalized version as:

To make the theory consistent with relativity,one must have the right-hand side of the above equation equal to zero when the scalar curvature or the background curvature vanishes.Thus,for a convenient option,we can set the four-vectoraμas,

where λ is a free parameter known as Rastall’s parameter.From equations (1) and (2),we can obtain the Rastall field equation as:

where β=κλ and,from hereafter,we shall term this as the Rastall parameter.The trace of the above equation gives,

The field equation in the presence of a non-vanishing cosmological constant is

whereEμνis the standard Einstein tensor.

3.Generalized AdS spherically symmetric black hole solution in Rastall’s gravity

To better approach the given model of Rastall gravity coupled to the term of rational nonlinear electrodynamics fields,we assume an ansatz for the spacetime geometry.Indeed,the spacetime metric is considered to be static,spherically,and symmetric in the following form:

wheref(r) is the metric function,which depends on the radial coordinater,and dΩ2=dθ2+sin2θdφ2.According to the spacetime structure,we assume a particular ansatz for the gauge field in the following form:

where the parameterQmstands for the total magnetic charge,and the quadratic invariantF is explicitly given by

The conjugate potential,meanwhile,may be redefined as

The definition of matter sector,involving a magnetic charge parameter to the black hole system,is a generalized term for both the type(I)and the type(II)classes of rational nonlinear electrodynamics fields.Incidentally,according to [74],the generic expression is perfectly expressed as

in which μ>0 is a dimensionless constant and α>0 carries the dimension of length squared.The generic formulation of the Lagrangian is a function of the quadratic invariant term F=Fμν Fμν,whereFμν=∂[μAν].A closer look reveals the following related expressions in the cases: ν=μ,2,1

It is interesting to note that,while considering the weak-field limit,new reduced expressions for the considered Lagrangian are generated in the approximate form as

Essentially,type (I) with the conditions (μ>1) and(0<μ<1) involves,respectively,a stronger and weaker vector field than the Maxwell vector field.Further,the case μ=1 gives rise to a pure Maxwell field in the weak-field limit.Similarly,thinking about type (II) as pointed out,it might be slightly stronger than the Maxwell field.Indeed,the preceding claim demonstrates that type (II) is a possible approach type of the Maxwell field in the weak-field limit,and is therefore the best candidate for the rational nonlinear electrodynamics source of black holes.

Let us now look at the gravitational and matter-source equations of motion (EOM).We can now obtain the following non-vanishing components of the field equation by defining the Rastall tensor from the field equation in equation (5) as Θμν=Eμν+Λgμν+κλgμνRsuch that

where the Ricci scalar reads as

Here,the prime denotes the derivative with respect to the radial coordinater.It is seen that the mixed Rastall tensor components Θ00=Θ11and Θ22=Θ33.This is the consequence of the spherical symmetric nature of the metric,equation (6),in the mixed tensor form.In this work,we would like to consider a general total energy–momentum tensorTμνdefined by

In this case,LFis the first derivative of the functionF.Meanwhile,the antisymmetric Faraday tensorFμνsatisfies the following nonlinear Maxwell equations

Proceeding with the matter part of the field equations,the energy–momentum tensor projection is now expressed as follows:

Therefore,the now-obtained set of EOM now provides an easy way to clearly define each component of the gravitational and matter sectors.To proceed,we will demonstrate the expression of the components (t,t),(r,r),(θ,θ),and (φ,φ).Thus,the Θtt=Tttand Θrr=Trrcomponents of Rastall field equations give,

whereH andG are expressed according to the terms

The present step is restricted to discovering a possible solution for the metric functionf(r);therefore,we use the differential set identified by the component(t,t).The approach to solving the second-order differential equation for the variable functionf(r) in this situation produces the following modeling solution:

where

andMis an integration constant standing for the mass of the black hole,andqis a free integration constant related to the magnetic charge,so that

Here,the hypergeometric function2F1(a,b;c;z),representing the regular solution of the hypergeometric differential equation,is defined for |z|<1 by a power series of the form2F1(a,b;c;z)=,where (n)kis the(rising)Pochhammer symbol[69].In fine order,the elements of the hypergeometric function employing the metric function are given as follows:

It is worth noting that according to[72],the Arnowitt–Deser–Misner (ADM) mass could be expressed as

Regarding the ADM mass term,or rather the condensate of the massless graviton,a close examination shows that the mass term is divided into two natures,one of which refers to the self-interaction involving the ordinary physical mass termM,and the second is nothing more than the nonlinear interactions between the graviton and the (nonlinear) photon,leading to a charge contribution α-1q3.

For a better understanding of the black hole system,it might be useful to collect all of the parameters into the parameter space.Thus,(M,q,μ,ν,β,Λ)expresses the underlying parameter space.Resuming some limits over the parameter space will allow us to find another black hole system.The limit(β=0),in particular,disables the presence of Rastall gravity,implying that the black hole is a solution in the frame of GR.At such considered limits,the black hole solution behaves as [17,71]

To conduct some analysis of nature’s singularities in relation to the physical solution,equation (20),the Ricci square (RμνRμν) and Kretshmann scalars (RμνλσRμνλσ) are needed

Using the metric function in our case,one can see that the scalars are not free from singularity issues.This is mainly due to the presence of the violation of energy–momentum conservation.

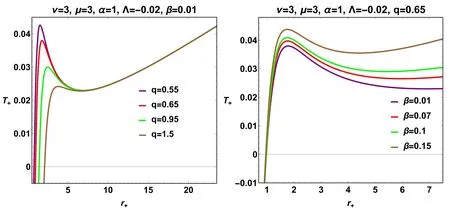
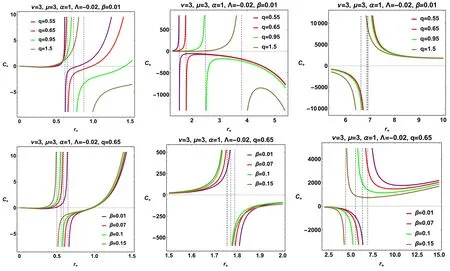
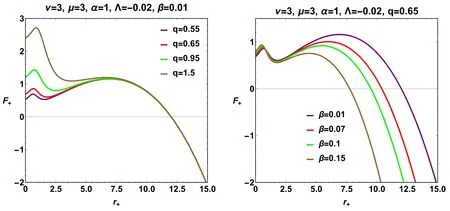
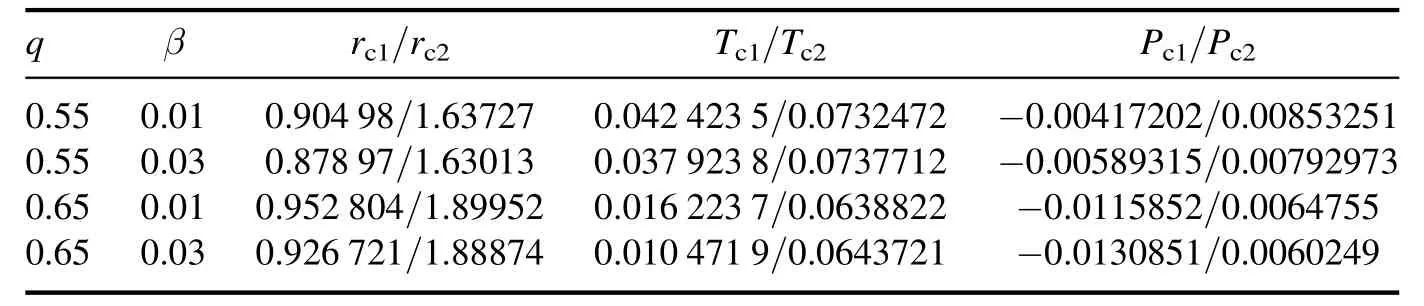
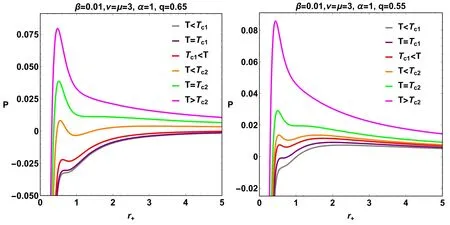
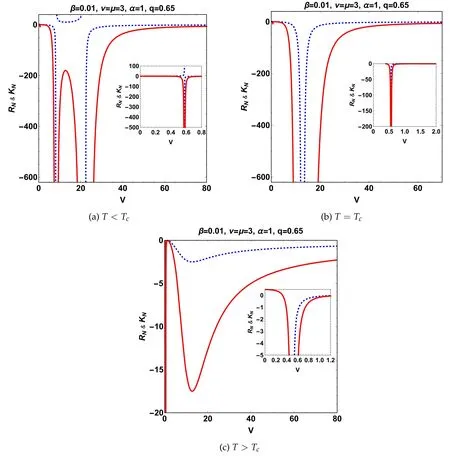
On the graphical side,the metric function is represented(figure 1) by taking into account two parameter variations,namely,β andq.It is interesting to set out some critical situations concerning the associated horizon structure.In this way,the variation of the parameter β involves some interesting behavior.In particular,according to the value of β,the number of possible sets of the horizon radius is dependent.Specifically,it is found that two critical scenarios exist in which the number of horizon radii changes.Hence,β=0.32 could generate four existing horizon radii,namely,the smallest root corresponds to two black hole horizons with an extra degeneracy smallest one,and the largest root is associated with a cosmological horizon.Moreover,for β>βc=0.32,the horizon set carries,at most,three or two horizon radii.However,β<βc=0.32 could generate one possible horizon radius.Meanwhile,the variation of the parameterq,in particular forq=0.8,generates,at most,three horizon radii,namely,two black hole horizons and the cosmological horizon.In addition,some critical issues are constrained by the critical valueqc=0.8,for whichq

4.Thermodynamic properties

Figure 1. Variation of the black hole metric function,equation(20),with respect to r for various values of(q,β)and for fixed values of(M,ν,μ,α,Λ,β).

Figure 2. Variation of the Hawking temperature T+(31)with respect to r+for various values of(q,β)and for fixed values of(ν,μ,α,Λ,β).

To study the thermodynamic properties in the normal phase space of the resulting black hole solution in depth,it is necessary to have an overview of the thermodynamic quantities in terms of mass,Hawking temperature,heat capacity,and Gibbs free energy,i.e.(M,T+,C+,F+).To construct these quantities,we first look for the mass of the black hole.At the radius of ther+horizon of the metric solution,equation(20),the mass of the black hole is given by

Within specific limits,the expression of the related black hole mass includes some other determined black hole masses.The situation of β=0 assists in the recovery of the specified mass for such a kind of AdS black hole in GR [71],which when combined withq=0 produces the Schwarzschild–AdS black hole mass [29].

The following step simply leads to finding the Hawking temperature.Taking into account the known surface gravity as

where ξμ=∂/∂tis a Killing vector.Thus,the formulaT+=κ/2π leads to finding the Hawking temperature as follows:

At some specific limits,the expression of the corresponding Hawking temperature yields alternative formulas.At the limit(β ∼0),the relevant Hawking temperature is confined to[71],and when combined withq=0,the Hawking temperature is unmistakably that of the Schwarzschild–AdS black hole[29].To see how the Hawking temperature behaves when the parameter space is a set of fixed values,we plot this behavior in figure 2.We always chose to represent the variation in terms of the parameter pair(q,β) .Remarkably,the Hawking temperature rises to a maximum atfor a specific point on ther+space,which grows depending on the variation of the parameter β.Basically,once the β-variation grows,thegrows,in contrast to theq-variation,which is disproportional to the growth of the.Moreover,further scrutiny reveals that the behavior of the Hawking temperature for essentially any parameter at smallr+is unphysically due to the negativity dubbedT+<0.Accordingly,the presence of negative regions in the temperature diagram simply has no physical justification [79,80]and,according to many works [78],this region can be removed by introducing the cut-off length in such a way that it does not conflict with quantum gravity.

It is advantageous to analyze and conduct a fascinating study for the thermodynamics aspect,keeping in mind the first law of thermodynamics in such a way that

where μiare the chemical potentials corresponding to the conserved chargesQi[73].

Implementing the first law with the given equations of mass and temperature produces an equation for the corresponding entropy.Entropy is defined clearly by

where we notice that the related entropy satisfies the area-law entropy.

When the robber got home and found no dog he thought He must have gone back to his old master, and, though night had already fallen, he went off after him

To inspect the stability of the black hole system,certain tools are emerging for this study.Predicting the local stability of our black hole solution as a first task is only possible based on the sign of the heat capacity.This function is given by

Likewise,the function is expressed in terms of the parameter space as

where

Within certain limits,as previously stated in the comments regarding the mentioning of thermodynamic variables such as mass and temperature,the corresponding heat capacity reduces.In both cases,β=0 andq=0,the heat capacity recovers that of [29].

To better analyze the behavior of heat capacity,figure 3 presents an appropriate analysis.It can be seen that the variation of parametersqand β generates a set of regions concerning the variation of heat capacity as a function of the horizon radius with a specific sign.Thus,the three sub-figures for each fixed parameter space imply five regions overall,in which three physical phase transition points(divergent points)and one physical limitation point (the root of heat capacity)are present.More specifically,the situation results in two types of sign changes of the heat capacity: either in a discontinuous way,where the divergent point is concerned,or by a continuous change generated by the physical limitation point.Essentially,the black hole system remains thermally locally stable since the sign of the heat capacity is positive.A close comparison between the pairs (q,β) shows that they have opposite behavior on the heat capacity function.

Figure 3. Variation of the heat capacity C+ (34) with respect to r+ for various values of (q,β) and for fixed values of (ν,μ,α,Λ,β).

Figure 4. Variation of the Gibbs free energy F+ (38) with respect to r+ for various values of (q,β) and for fixed values of (ν,μ,α,Λ,β).

The second task has the objective of predicting the global stability of our black hole solution.As a result,Gibbs free energy is the sole technique that involves specific global stability.The appropriate Gibbs free energy expression in normal phase space is given for this purpose as

or,more precisely,in terms of the parameter space,the functionF+is re-expressed as

In this case,the Gibbs free energy includes other expressions across the reducing parameter space.The cases(β=0,q=0),in particular,lead to the knowing expressions.

The usefulness of Gibbs free energy demonstrates whether the black hole system is globally stable or unstable.For that reason,figure 4 shows the variation of the Gibbs free energy against the horizon radius,which claims that the black hole system is unstable at smallr+(F+<0),while the positive sign of the Gibbs free energy(F+>0)dominates;hence,the black hole system remains globally stable.The presence of such a minimum o maximum(rmin,max),indicating the extreme point of the Hawking temperature on the other side,is a key feature in this figure.

5.Extended phase space

To perform the intended phase transition,the first law of thermodynamics must be in the extended version.Thus,the first law is appropriately given as

where Π intervenes as a novel quantity conjugate to α.Explicitly,it is defined by

To construct the thermodynamic phase space framework,in particular,the parameter functionf(r+,M,p,q,α) must still vanish under any transformation of the parameter.Further remarks on this subject make similar arguments to consider the constraintsf(r+,M,p,q,α)=0 and δf(r+,M,p,q,α)=0 on the evolution along the space of the parameters.Nevertheless,an alternative way is considered: taking the mass parameter,M,as a function of the parametersM(r+,ℓ,Qm,α) too.

The thermodynamic parameters areS,p,Qmand α.It is then convenient to redefineM=M(S,p,Qm,α) for the possibility of explicitly obtaining

This is similar to such a differential 1-form in the space of parameters.Clearly,all of the components are nothing more than thermodynamic quantities,like temperature,thermodynamic volume,electric potential,and the parameter of the nonlinear electromagnetic field given respectively in the form

In an alternative way,the same results can be expressed in accordance with the variation along the space of the parameters of the condition described byf(r+,M,P,Qm,α),

reshaping another term for dMgiving,as follows:

Table 1. Numerical sets for critical physical quantities (rc,Tc,Pc) with ν=μ=3 and α=1.

which must conform with equation (40).Equation (48)embraces the presence of temperature,which is geometrically defined as

which is a well-known finding,providing

It should be pointed out that this expression can also be derived using Wald’s formalism;basically,δS=as long as df=0 is satisfied.

Furthermore,the thermodynamic volume,the electric potential,and the conjugate potential are defined by the following formula:

In the black hole system,the enthalpy is defined by the total mass of the system.The thermodynamic volume can thus be computed as

According to Euler’s theorem [70],withM(S,P,Qm,α),the Smarr formula can be constructed for the charged source in Rastall gravity given by

in which the parameter α of the nonlinear electromagnetic field behaves as a thermodynamic variable.

By exploiting the Hawking temperature expression together with equation (39),we can obtain the corresponding equation of state for the black hole system as follows:

Of course,the parameters β,α,μ,and ν potentially affect this equation.As intended,we can define the specific volumev=2r+,wherewith the pressure is cast in the standard formP=+O (v).Moreover,since the thermodynamic volumeV∝,the critical point can be determined by

or alternatively,

Using the constraints mentioned above permits the discovery of the critical configuration point (Tc,Pc,rc),which could be generated by considering the next equation with the unknownrc,equation(61).Therefore,the critical set can be defined as follows:

Approaching the critical behavior numerically is achieved by solving equation (61).Thus,table 1 collects,for various fixed parameter spaces,the numerically critical point.It is well observed that the associate critical set involves two physical critical points,and hence some complicated interpretations will appear compared to the standard case of theP–Vcriticality.

It is important to recall that in the limit β→0,where the Rastall gravity is not present in the studied frame,the present state equation reduces to that defined in GR expressed by

Exploiting the above equation with condition 32,the critical point will be explicitly defined as

• type (I):

• type (II):

• Maxwellian type:

where finding the root asrcleads to the definition of the critical triplet (rc,Tc,Pc).

To evidence theP-r+criticality behavior,we plot theP-r+diagram in figure 5 for various values of Hawking temperatureT.Figure 5 shows that for certain values of the parameter space,two critical points exist: one refers to negative (unphysical)pressure and the other refers to positive pressure.The obtained curves on theP-r+diagram are moderately more complex than those of the standard van der Waals,reflecting the important behavior of Gibbs free energy.Thus,at a small value ofr+,the isotherms behave like van der Waals behavior,while at a large value ofr+,the isotherms turn and lead back to a region with negative pressures.The isothermal plots regarding this situation are perfectly similar to theP–Vdiagram of Born–Infeld–AdS black holes[76].A comparative study of the parameter charge shows that once the charge parameter increases,the maximum along theP-r+curves decreases.

Figure 5. The isotherm P-r+ of the black hole system for certain values of the parameter space.

Figure 6.The G–T diagram of the black hole system for certain values of the parameter space.Critical data:(TTr=0.0448,PTr=0.0024087)and (TZ=0.0573,PZ=0.00425724).

Figure 7. Graphs of the normalized thermodynamic Ricci scalar(solid red curve)and extrinsic curvature(dashed blue curve)as a function of thermodynamic volume V.

The next step will be to perfectly disclose the corresponding phase transition of a system via its thermodynamic potential.In particular,Gibbs’s free energy is a thermodynamic quantity computed from the Euclidean action with an appropriate boundary term.A fruitful feature resulting from the sign of Gibbs free energy enables an analysis of global stability.In the extended phase space,the thermodynamic potential is now Gibbs free energy,G=M-T S.In practice,it is worth noting that any discontinuous behavior in first-or second-order derivatives of Gibbs energy results in a first-or second-order phase transition in the system.Therefore,the appropriate Gibbs free energy expression in extended phase space is given for this purpose as

The appropriate Gibbs behavior with two critical points,is shown in figure 6.In a detailed discussion,the figure at the top left shows the behavior of theG–Tcurve forPc1=–0.0803596<0,which is a thermodynamically unstable branch with negative heat capacityCp<0.In thePPc2,the system displays no phase transitions.Therefore,the critical point with negative pressure does not globally minimize the Gibbs energy,which is not a physical point,while the second critical point minimizes the Gibbs free energy.

5.1.Critical exponents

Critical exponents neatly portray the behavior of physical quantities in the vicinity of the critical point.This is because critical exponents are independent of physical systems and can be considered as quasi-universal parameters.It may help to consider the following key notations:

wherein the critical thermodynamic volumeVcis assigned to the critical horizon radiusrcbyVc=.In this way,the critical exponents are spelled out explicitly as follows:

The exponent α specifies the behavior of specific heat at constant volume.A simple conclusion is that the entropySis independent of the Hawking temperatureT,hence

so we can deduce that α=0.

The exponent β captures the behavior of the order parameter near the critical point.In this case,the equation of state near the critical point can be developed as

where

with

Therefore,in terms of numerical results,the dependencies of the coefficientsaiupon the parametersqand β are displayed in table 2.Given that the pressure remains constant during the phase transition,the following satisfies:

where ωsand ωlare the reduced volumes of the small and large black holes,respectively.

On top of this,Maxwell’s equal-area law is quite easily stated as follows:

while taking into account the first derivative,so that

Using equations (72) and (73) yields

Table 2. Numerical sets for the constants ai with ν=μ=3 and α=1.

Whereupon,and taking into account equation (71),we may find an explicit link between ωland ωsas follows:

where the argument under the square root function remains positive.A quick look at equation (75) gives the expected results,namely

which provides λ=1/2.

The exponent γ is used to assess the critical behavior of the isothermal compressibility κT,stated in terms of

which results in γ=1.

The exponent δ is responsible for describing the critical behavior of equation (68) on the critical isothermT=Tc.Consequently,the shape of the critical isotherm is set att=0,leading to the following results:

which proves δ=3.

By considering the previous treatment,it is obviously noted that the four exploited critical exponents are those computed for the case of the charged AdS black holes.This does,in fact,prove that the rational nonlinear electrodynamic contribution within the context of Rastall gravity cannot change the critical exponents.Consequently,the present study provides physical similarities along the realm of theP–Vcriticality.

6.Thermodynamic geometry

Showing the nature of interactions among black hole microstructures is appropriately the main goal of this section.For this purpose,the exploitation of the Ruppeiner geometry permits carrying out such interpretations in that sense.Essentially,the Ruppeiner formalism provides valuable information on the internal dynamics of considered thermodynamic systems by inspecting the sign of the corresponding metric curvature.In practice,the dominant attractive (repulsive) micro-interactions are qualitatively identified from the Ruppeiner negative (positive) scalar curvature.Whereas non-interacting systems like ideal gas are set in whenever the Ruppeiner scalar curvature is vanishing.

Therefore,we investigate the thermodynamic geometry in the extended phase space.The previous critical finding is used to perform the associated geothermodynamic analysis.Hence,the probing analysis consists of taking Helmholtz-free energyF=U-TSas an appropriate thermodynamic potential andXi=(T,V)as a thermodynamic variable that is either intensive or extensive.The first approach,meanwhile,entails dealing with the following thermodynamic metric:

together with the injection of the differential form of free energy,dF=–SdT+PdV,into the corresponding metric,yields

whereCV=T(∂TS)Vis the specific heat capacity at the constant volumeV.The requirement for the application of the Ricci scalar is the revelation of a correspondence with the phase transition points of the heat capacity.Indeed,at these points,the Ricci scalar diverges.The use of the related metric in equation (79) gives an expression for the Ricci scalar as

A quick examination shows that the equation of state depends linearly on the temperatureT;thus,any derivation up to the second-order inTvanishes.The resulting expression for the Ricci scalar is formalized as follows [77]

The situation for studying thermodynamic geometry offers indepth further tools,namely,the extrinsic curvature.Indeed,extrinsic curvature for the metric in equation (79) may be represented as follows [75]

Within the framework of a given van der Waals fluid,the specific heat capacity at a constant volume isCV=3/2kB.It is straightforward thatCV==0and,as a consequence,in the following,we will employ the normalized form of curvatures as

which can be rewritten explicitly in terms of the parameter space of the black hole system and with the thermodynamic variablesTandVas

The behavior of normalized quantities such as the Ricci scalar and extrinsic curvature is depicted in figure 7 against the thermodynamic volume.Discovering a particular description for the associated phase transition involving the presence of the Ricci scalar is the main task of this part.Concretely,the phase transition takes place at the singularities of the scalar curvature: hence,predicting a repulsive interaction between the microscopic black hole molecules in scenarios dealing withRN>0.

It is remarkable from figure 7 to note that forTTc),the singular behavior gets shrunk until it disappears completely.For small values ofV,a remark takes place concerning the existence of a divergent point,despite the temperature changes in all three compared situations.Additionally,throughout the critical processes,the normalized Ruppeiner curvature scalar turns out to be negative (RN<0),indicating the existence of attractive interactions among the black hole microstructures.

7.Conclusion and summary

In this paper,we have constructed a black hole solution with a generalized distribution charged matter source within the Rastall gravity framework.The obtained solution has a number of horizons,depending on the value of the parameter space(M,q,μ,ν,β,Λ).The considered matter sector,in GR,makes a possible distinction between known kinds of rational nonlinear electrodynamics black holes,namely type(I) or type (II),in terms of μ and ν parameters,and,at the limit ν=1,where (ν=μ),the obtained solution shows a Maxwellian charged matter source.We have studied,in the normal phase space,the thermodynamic properties,and we have shown analytically and graphically the temperature behavior,heat capacity,and Gibbs free energy.A more detailed analysis concerning global and local stability was conducted by the sign pertinent to heat capacity and Gibbs free energy.As the main goal of this paper is to study the critical behavior of our black hole solution,we have examined the phase structure in which the first law of thermodynamics is extended by adding theV dPterm,where the cosmological constant Λ is considered to be the pressureP.Furthermore,the critical behavior is investigated along theP–Vdiagram where,at a small value ofr+,the isotherms exhibit van der Waals behavior;meanwhile,at a large value ofr+,the isotherms turn around and lead again to a region where the pressures are negative.Using the same objective,we have analytically and graphically treated the behavior of the Gibbs free energy in the extended phase space,and we have found that there are two critical points with two pressures at which the re-entrant phase transition occurs and disappears.For the next step,we have investigated the thermodynamic geometry using the Ruppeiner formalism.Within the context of this process,we have demonstrated the normalized quantity for the Ricci scalar as well as the extrinsic curvature.As a result,the normalized Ricci scalar indicates all the possible pointphase transitions of the heat capacity,and the normalized extrinsic curvature has the same sign as the normalized Ricci scalar.

This work comes up with certain issues and will be a topic for revealing the quasi-normal modes and shadow behavior,as well as the deflection angle.

Acknowledgments

This work was supported by the Ministry of Science and Higher Education of the Republic of Kazakhstan,Grant AP14870191.

ORCID iDs