Holographic dark energy in non-conserved gravity theory

H R Fazlollahi

Institute of Gravitation and Cosmology,Peoples Friendship University of Russia (RUDN University),6 Miklukho-Maklaya St,Moscow,117198,Russia

Abstract Recently,reconsidering the Rastall idea =a,μ through relativistic thermodynamics gives a new form for the scalar fielda which led us to construct modern modified theory of gravity debugged ‘non-conserved gravity theory’ Fazlollahi 2023 Euro.Phys.J. C 83 923.This theory unlike other modified theories of gravity cannot directly explain the current acceleration expansion in the absence of the cosmological constant and or existence of other forms of dark energy.Hence,in this study we have reinvestigated holographic dark energy ρX～H2 in the non-conserved theory of gravity.In this context,the density and pressure of dark energy depend on the non-conserved term and density of the dust matter field.As shown,due to nonconservation effects on large-scale structures,unlike the original holographic model,our model onsets an acceleration epoch for the current Universe satisfies observations.Moreover,the interaction and viscous scenarios are studied for this model.

Keywords: non-conserved gravity,covariant form of thermodynamics,holographic dark energy

1.Introduction

The current acceleration expansion of the Universe is one of the puzzles in modern cosmology.Reviewing general relativity and its field equations shows that the matter-radiation field,due to its gravitational effects,cannot explain current acceleration epoch.Keeping general relativity and its deep analyzing also reveals that the Universe may include another component with negative pressure [2].The cosmological constant Λ as its simplest form can present such a field in large-scale structure with a constant equation of stateωΛ=-1[3].However,this model suffers from two theoretical (fine-tuning) and cosmological (coincidence) problems [4].In this context,a dozen different approaches are presented to alleviate these problems.

The modified theories of gravity are one of these straightforward scenarios.In such theories the usual Einstein–Hilbert action modified by different scalar terms built by the Riemann tensor and its derivatives [5–8],curvature-matter interaction terms [9–11] and or non-Einsteinian matter field[12,13].As result,dark energy given as extra terms in Friedmann equations depends on some linear and/or nonlinear relation between geometry and matter.Although in most of these models,the modified theories of gravity support observations,there is no strong evidence around the validity of them,theoretically.For instance,according to the Rastall idea,one may assume that the conservation law is broken in curved spacetime and thus there is a flux of energy-momentum in non-flatness geometry due to the gravitational field[14].This idea may open new windows to investigate field equations in high levels of gravity energy.However,this proposal in which the flux of the energy-momentum is proportional to the scalar curvatureRis questionable.

Studying relativistic thermodynamics in this case may give some robust clues in finding the flux of the energymomentum tensor in special relativity,theoretically [15].As discussed in[1],generalizing this model into curved spacetime yields a new modified theory of gravity that satisfies the main Rastall idea,≠0,in which a fulx of energy-momentum is given by the evolution of thermodynamical parameters and not the scalar curvature.Although such a theory of gravity alleviates the coincidence problem of the cosmological constant model,in the absence of a dark energy model when we face with the pure non-conserved theory of gravity,this alternative theory cannot explain the current acceleration phase.This issue traces back to its behavior in the Friedmann–Robertson–Walker Universe;one can assume extra terms in the time component of the field equation as density of dark energy,but there is no corresponding terms in the second Friedmann equation as pressure of dark energy.Unlike other alternative theories of gravity,it shows that the pure nonconserved theory gives no dark energy,directly.As a result,to investigate late-time Universe one needs to add the density of dark energy by hand.Hence,in this study,we will study one of the candidates of dark energy in a non-conserved theory of gravity,in which the density of the dark energy comes from the fundamental properties of quantum circumstance.Inspired by the investigation of the thermodynamics of a black hole [16],Hooft proposed the famous holographic principle [17].According to this principle all of the information contained in a volume of space can be given as a hologram,which corresponds to a theory located on the boundary of that space.With this principle,Cohen and his collaborators suggested that in quantum field theory,a short distance cut-off is related to a long-distance cut-off due to the limit set by formations of a black hole[18].With this idea at hand,the energy density of an unknown field is proportional to the square of the cut-off length,inversely i.e.,ρ0≈ℓ-2.A related idea was discussed in[19,20],whereinρ0given by the Hubble scale,ℓ=H-1.This selection alleviates the fine-tuning problem in which dark energy is scaled by the cosmological parameter and not the Planck length.However,this cut-off selection cannot explain the acceleration expansion of the Universe in late-time [21].Consequently,it is worthwhile to explore such a model of dark energy in non-conserved theory and check whether this theory solves this problem or not.

The contents in this paper are organized as follows.In section 2,the non-conserved theory of gravity is revisited,briefly.In sections 3 and 4,late-time cosmology when the density of dark energy is given byρX～H2is studied for noninteraction and interaction scenarios,respectively.We also explore viscous scenario in section 5.Remarks are given in section 6.

2.Covariant thermodynamics and new gravity models

The transformation of heat and temperature in relativity theory under the Lorentz group is one of the unsolved issues and opening topics in this theory.For instance,Einstein and Planck proposed [22,23]

while Ott and Arzelies proposed another transformation form[24,25]

whereδQandTdenote heat and temperature,respectively,the variables with subscript0 represent those observed in the comoving frame,andγis the Lorentz factor.In addition to these options,Landsberg suggested that heat and temperature behave as absolute parameters and thus comoving and independent observers measure the same heat and temperature[26].However,just two first options,(1)and(2),can satisfy a relativistic Carnot cycle[27].The covariant form of relativity theory,in particular,may be essential to formulate relativistic laws of thermodynamics.In this context,one of the pioneer attempts are given by Israel and collaborators [15]:

where the number of 4-vector=njiuμ,represents the flux densities of conserved chargesjfor componenti-th andexpresses the 4-flux of entropy of fluidi-th.βν=uν/T0presents the inverse temperature 4-vector proposed by Van Kampen [28],andαj=ζj/T0.The parameterζjdenotes the relativistic injection energy or chemical potential per particle of typej,related to its classical counterpart by:

It is to be noted that the 4-vectorSμfor the flux of entropy behaves in a similar way to the 4-vector for the flux of particle number.So,like the particle number that is the scalar for the comoving observer,it is shown that entropy in its comoving frame is a scalar as well[29].As a result,this model is not in conflict with the standard expression of thermodynamical expression only when it is considered in a comoving frame.Relation (3) not only shows that Rastall’s idea is true in curved spacetime,but it is valid even in Minkowskian geometry when the flux of energy-momentum tensor is given as evolution in entropy and temperature of the whole system.

To expand this model to curved geometry,one just needs to apply the principle of general relativity [1],

in which the usual (scalar) derivative is replaced by the covariant derivative.To derive and find the total energymomentum tensor,one only needs to use definitionsβν=uν/T0andαj=ζj/T0,which yields

Such a relation shows that the flow of the energy-momentum tensor is a function of the thermodynamical parameters entropy,temperature,and mutual interaction among all participating particles.Equation (6) actually proves Rastall’s idea,not only in the presence of the gravity but also for Minkowskian geometry.It should be noted that since the energy-momentum tensor in general relativity is a symmetric one,the right-hand side of equation (6) is also a symmetric tensor.

The general relativity principle is applied and after some manipulations,the field equations can be derived as such

whereκ′ is the proportional constant.Taking a covariant derivative of the above field equations and usingGμν;μ=0 recasts equations (6) to (7).Defining the non-conserved term for each component participated in our system as

let one have compact form for field equation (7),namely

which shows each fluid (component)plays an explicit role in the field equations.Summation on all different components participating in the system (summation on indexi),yields,

where we denote the effective termsthrough

whenX=ℇ and/orT.

Since these field equations must shrink to standard Einstein field equations without losing generality,one can assumeκ′=κ.

In the following we assume that the Universe is a homogenous and isotropic medium and describe with the Friedmann–Robertson–Walker metric

wherea=a(t)is the cosmic scale factor andk=0,1 and -1 corresponds to the flat,close,and open Universe,respectively.Observations confirm that the Universe is flat and thus we assumek=0.With the aid of this assumption and using field equation (10),the Friedmann equations become

in which we consider the matter as a dust field and subscriptsmandXdenote the matter and dark energy fields,respectively.

With these Friedmann equations at hand,we will consider late-time Universe for non-interaction and interaction scenarios in the next two sections while dark energy density is given by theαas an arbitrary constant

At the end of this section,we encourage interested readers to see the main paper of the non-conserved theory of gravity to review and check the effects of the cosmological constant and also the evolution of the Universe in the inflation era [1].

3.Non-interaction scenarios

In this section,at first glance we will consider the Friedmann equations (13) and (14) for dark energy density given by equation (15) when there is no interaction between matter and dark energy.Plugging equation (15) into the first Friedmann equation (13) and solving it for the Hubble parameter yields,

Comparing the Hubble form (16) and density (15) directly reveals that the density of dark energy depends on the matter field and thus the coincidence problem alleviates.Moreover,if both density of matter and non-conserved termcan be positive,to have the valuable Hubble parameter,one finds out

Definingx=ln(a) and taking a derivative with respect toxfrom the first Friedmann equation and using its result in equation (14),gives the continuity equation

To reconstruct the standard density of matter,one may decouple the above equation as follows:

whereQrepresents the mutual interaction between the dark energy and matter field.With some computations and using the above equations,one finds:

This expression of the pressure of the dark energy shows that in the non-interaction scenario,pXis just the function of the non-conserved termand its first derivative.As a result,equation(21)illustrates that the origin of the pressure of the dark energy is a non-conservation term in our model.

In the absence of enough microscopic observations of the interaction term,one may attempt to consider field equations (13) and (14) whenQ=0,(non-interaction scenario).However,since we are faced with an extra parameterin our model,in this step it is necessary to have a valuable form for that.Reconsidering equation (8) reveals that it includes two parts:T0Stand all interactions among particles.Keeping to the second law of thermodynamics shows thatT0Stmust grow up with time,and thus it can be given byeγxin whichγ>0,while due to relation (4),the second part is proportional to the density of the matter field,namely

Consequently with these assumptions for the expanding Universe,we may suggest that

whereβandηare proportional constants.

As a result and in the absence of the interaction term,Q=0,the density of the matter,and the density and pressure of the dark energy are,

respectively.

For such a dark energy model,the equation of the state and deceleration parameter given by:

To constrain the model with current observations,we setH0=67.4,Ωm0=0.315 andωX0=-1[30],wherein Ωm0is a current fractional density of the dust matter,defined by

Hence,and by using equations (16) and (27),two free parametersβandηbecome

In order to constrainα,one may use the approach given in[31,32].In such an approach,defining the transition redshift

with the aid of the deceleration parameter(28)obtainsαas a function ofxTwhenq(xT)=0is used

The joint analysis of SNe+CMB data and the Λ cold dark matter (CDM) theory obtainszT=0.52-0.73[33].With this range at hand,the free parameterαis given by these observations.

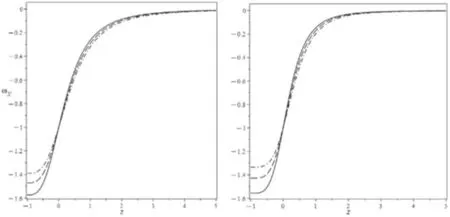
Figure 1. The equation of the state of the dark energy in the noninteraction scenario when H0=67.4 and Ωm0=0.315 and γ=0.1(left panel) and γ=1.1(right panel) for zT=0.52(solid curve),zT=0.62(dashed curve) andzT=0.72(dash-dotted curve).

Figure 2. Deceleration parameter in the non-interaction scenario whenγ=0.1(left panel) andγ=1.1(right panel) forzT=0.52(solid curve),zT=0.62(dashed curve) andzT=0.72(dash-dotted curve).

In figures 1 and 2 the evolution of the equation of the state and the deceleration parameter as a function of the redshiftzforγ=0.1and 1.1 are plotted1With these values of γ,the condition (14) is satisfied..As shown,our model is valuable due to the non-conservation effects presented,while in the absence of the non-conservation term,the holographic dark energyρX=αH2evolves like pressureless matter during the expansion of the Universe,ωX=0[21],and thus it cannot explain the current epoch.As plotted in figure 1,the dark energy in this model behaves like a dust matter field in the past Universe,coinciding with Λ CDM theory atz=0 and evolving like a phantom fluid in the future.From figure 2,sinceq→0.5forz≫0,there are no deviations in matter structure formation during the matterdominated era.Furthermore,restrictingαwith a transition point shows that the model is not in conflict with the observations [33].

To explore the effects of the perturbations on the classical stability of the model,the speed of sound squaredshould be positive and ≤1.

With the aid of equations (30) and (31),one obtains

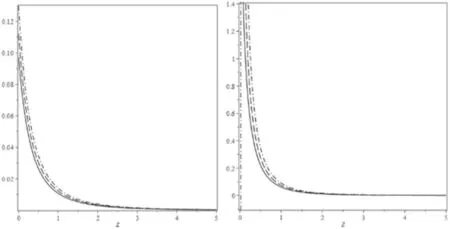
Figure 3. The speed of sound squared versus the redshift for the noninteraction scenario whenγ=0.1(left panel) andγ=1.1(right panel) for zT=0.52(solid curve),zT=0.62(dashed curve) and zT=0.72(dash-dotted curve).

As discussed in this section,it is revealed that the nonconservation term alleviates the original holographic model of the dark energy problem in which it can onset a trigger of current acceleration expansion.

In the two next sections,we will explore the interaction and pure viscous scenarios for our model.

4.Interaction scenarios

In this section,we assume that the interaction termQ≠0,given byQ=c1(ρm+)in whichc1,is an arbitrary constant.With this assumption,and using equations (16) and(19),the density of the matter field and dark energy is given by

As a result,the pressure for the corresponding dark energy becomes

Consequently,with the same initial conditions constraining model with the current values of the Hubble parameter and the fractional density of matter,one has

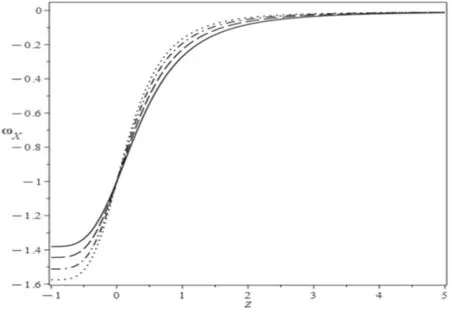
Figure 4. Equation of state for the interaction scenario when H0=67.4,Ωm0=0.315andc1=α=0.1is used for γ=0.47(solid curve),γ=0.63(dashed curve),γ=0.8(dash-dotted curve)and γ=0.96for dotted curve.

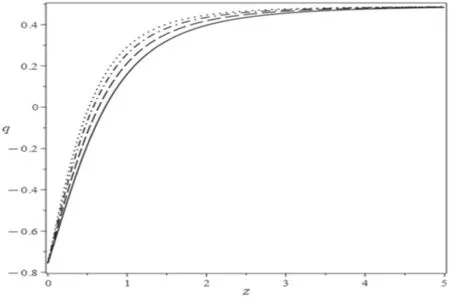
Figure 5. The deceleration parameter versus the redshift when H0=67.4,Ωm0=0.315andc1=α=0.1is used for γ=0.47(solid curve),γ=0.63(dashed curve),γ=0.8(dash-dotted curve)and γ=0.96for dotted curve.

The volution of the equation of state,deceleration parameter,and speed of sound squared for this scenario is plotted in figures 4–6,which depicts that the model is not in conflict with the Λ CDM theory.As shown in figure 3,this model presents quintessence dark energy fluid and behaves like dust matter in high redshift while coinciding with the Λ theory atz=0.Investigating the deceleration parameter just shows that the transition point in the interaction scenario satisfies the observations (see figure 4).

Figure 6. Speed of sound squared as the function of the redshiftz for γ=0.47(solid curve),γ=0.63(dashed curve),γ=0.8(dashdotted curve) and γ=0.96for dotted curve when H0=67.4,Ωm0=0.315andc1=α=0.1..

5.Viscous model

In this section,we study the bulk viscosity on holographic dark energy in the non-conserved theory of gravity.The bulk viscosity scenario is introduced by dissipating just through redefining the effective pressurep[e]=p-ζHwhereζis the bulk viscosity coefficient.

In the absence of interaction between the dust matter field and the dark energy,using equation (18) yields the effective pressure of viscous dark energy as

Here,we are interested in exploring the Universe dominated by a dust matter field and the holographic dark energy given in equation (15).In the following and as a toy model,we assume thatζ=.Hence,with aid of equation (15),the bulk viscosity term is given by

Computing the equation of state,deceleration parameter and speed of sound squared,one finds

in which the prime denotes the derivative with respect toxand we defineωX0=-1,we have

Constraining the model for the current Universe,x=0,when

Figure 7. Equation of the state versus the redshift for zT=0.52(solid curve),zT=0.55(dashed curve) and zT=0.58(dash-dotted curve).

Figure 8. The evolution of the deceleration parameter as a function of the redshift for zT=0.52(solid curve),zT=0.55(dashed curve)and zT=0.58(dash-dotted curve).

Using transition point (32) for deceleration parameter (46)obtains

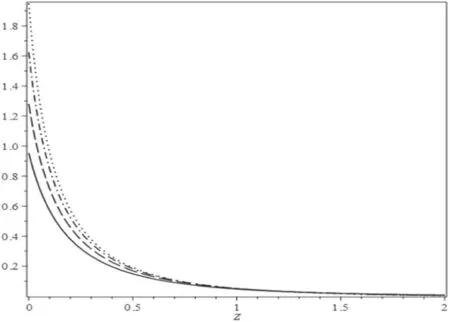
Figure 9. The speed of sound squared for the viscous model when we use zT=0.52(solid curve),zT=0.55(dashed curve) and zT=0.58(dash-dotted curve).

In figures 7–9,the evolution of the parameters given in equations (44)–(46) are plotted when we setβ=110andγ=0.1.As shown,the viscous dark energy gives another way to alleviate the transition point while the dark energy evolves as matter fluid in the past Universe to a cosmological constant-like model inz=0 and behaves like a strong phantom field in the future.

6.Conclusions

To summarize,we have considered the original holographic dark energy in a new modified theory of gravity,‘non-conserved gravity’.As discussed,in this theory the Rastall idea is reconsidered and shows that the energy-momentum tensor is not conserved when its flux is given by thermodynamical parameters of the system.Also,such a theory cannot present a current acceleration phase alone,and thus one needs to dilute the theory with other modified theories of gravity or add some parameters of dark energy by hand.

In this study,we have attempted to check the original holographic dark energy in which a cut-off length is proportional to the inverse of the Hubble parameter,i.e.,ℓ=H-1.This model of dark energy cannot onset a late-time acceleration epoch in standard gravity theory as shown,due to the effects of the non-conservation term in our model,such a scenario of dark energy can explain the present phase.As discussed,in both non-interaction and interaction scenarios,the model presents dark energy which behaves like the cosmological constant atz=0,while for high redshifts it evolves as dust matter.However,such quintessence dark energy behaves as a phantom field in the future Universe.Futhremore,this dark energy is stable,wherein for both scenarios one finds≥0.

As another plausible scenario we have studied the viscous model.As shown,this scenario also satisfies our observations.In this scenario,the dark energy,due to its viscosity,presents matter with positive pressure in the past Universe while in the current Universe,it coincides with the Λ CDM model.

We encourage any interested researchers to apply another dark energy model in the non-conserved theory of gravity to investigate and check this theory theoretically and observationally.

Acknowledgments

The authors thank A H Fazlollahi for his helpful cooperation and comments,and the referee(s)for their considerations also.

ORCID iDs