Theoretical study of the nonlinear forceloading control in single-molecule stretching experiments
Xingyu Qi ,Zilong Guo ,Shimin Le and Hu Chen
1 Research Institute for Biomimetics and Soft Matter,Fujian Provincial Key Lab for Soft Functional Materials Research,Department of Physics,Xiamen University,Xiamen 361005,China
2 Center of Biomedical Physics,Wenzhou Institute,University of Chinese Academy of Sciences,Wenzhou 325000,China
Abstract Force spectrum measurements with constant loading rates are widely used in single-molecule manipulation experiments to study the mechanical stability and force response of biomolecules.Force-dependent transition rates can be obtained from the transition force distribution,but it is limited to the force range with non-zero force distribution.Although constant loading rate control can be realized with magnetic tweezers,the loading rate range is limited due to the slow movement of permanent magnets.Non-linear exponential and exponential squared force loading functions are more feasible in magnetic tweezers,while there is no theoretical result available for these two kinds of non-linear force loading functions.In this study,we solved the unfolding process of a protein following Bell’s model under nonlinear exponential and exponential squared force loading functions,which offer a broader range of unfolding force distribution compared to the traditional constant loading rate experiments.Furthermore,we derived two force loading functions,which can produce uniform unfolding force distribution.This research contributes fundamental equations for the analysis of experimental data obtained through single-molecule manipulation under nonlinear force loading controls,paving the way for the use of nonlinear force control in magnetic tweezer experiments.
Keywords: single-molecule manipulation,magnetic tweezers,force loading,transition rates,force distribution
1.Introduction
The relationship between mechanical force and the structural transitions of biomolecules has always been a focus in biophysical and mechanobiology researches.Over the years,single-molecule manipulation experiments have emerged as an important technique to measure the mechanical stability and force response of biomolecules[1–9].In single-molecule manipulation experiments,the force-dependent conformation transition rates of biomolecules are the most important data to be measured [10].The force range is always desired to be as wide as possible since it is important to reveal the detailed information of the underlying free-energy landscape,which determines the dynamic properties of biomolecules [11].
Constant loading rates and constant pulling speeds are usually applied in magnetic tweezers (MT) and atomic force microscopy (AFM)/optical tweezers (OT) experiments,respectively [1–9].These measurements have provided kinetic parameters of various molecular systems [3–6].In the case of constant loading rate in MT experiments,the unfolding force of proteins can be derived as an analytical equation for biomolecules following Bell’s model.The equation can be used to fit the experimental data to obtain kinetic parameters such as unfolding distance and zeroforce unfolding rate [12,13].On the other hand,constant pulling speed experiments using AFM and OT can generate an average loading rate within a certain range.Although not very strict,the same analysis method can be used to obtain the kinetic properties [1].

Figure 1. Schematic diagram of magnetic tweezers setup.(a)The force exerted on a protein molecule by a magnetic bead within the magnetic field of the double magnets.(b)The relationship between the force F and the distance d between the magnets and the paramagnetic bead is assumed to be F(d)=200 exp (-3d)pN,where d is in units of millimeters.
However,a significant limitation with the constant loading rate method is that the extracted force-dependent transition rates are confined to limited force range with nonzero force distribution.To obtain transition rates over a large force range,different loading rates with orders of magnitude difference usually need to be applied [14].Force is approximately an exponential function of the distance between permanent magnets and the sample in MT [figure 1].Therefore,the magnets need to move nonlinearly to obtain a constant loading rate with an initial fast speed,which makes the mechanical control complex and limits the range of loading rate feasible in MT [15].
Another experimental strategy is to measure the waiting time of transitions at a series of constant forces.At forces with slow transitions,the stability of the equipment is crucial for the measurement.MT has the advantage of stability for longtime measurements over AFM and OT [3,7].On the other hand,if the transition is very fast,the process of the force jumping will give a dead time of measurement,which limits the fastest measurable transition rate [16].
In this study,we venture beyond the traditional realm of constant loading rate or constant force measurements and study the consequence of nonlinear force-loading controls.First,we derived the unfolding force distribution under exponential or exponential squared force-loading functions for Bell’s model.Second,a theoretical force versus time function was derived to render a uniform unfolding force distribution.By integrating traditional methods with innovative nonlinear force control,accurate unfolding rates can be achieved over a broader force range to enhance the efficiency of single-molecule manipulation experiments.
2.Model and methods
2.1.Force-dependent unfolding rate ku(F)
We conventionally conceptualize the unfolding of a protein as a process of overcoming a free-energy barrier[17,18].As the barrier height is affected by the stretching force,the unfolding ratekuis dependent on stretching forceF.In this study,we suppose that the unfolding transition of a protein follows Bell’s model,whose force-dependent unfolding rate is given by [12],
wherek0denotes the zero-force unfolding rate,xuthe unfolding distance,i.e.the distance between the native state and transition state,β=1/kBT,kBthe Boltzmann constant andTthe absolute temperature.In this study,unless otherwise specified,we set parametersk0=0.005 s-1andxu=2 nm.
2.2.Force-loading function F(t)
The force-loading function,F(t),defines the forceFas a function of timet.The linear force-loading function:
whereF0denotes the initial force andrthe loading rate.Two kinds of nonlinear force-loading functions under scrutiny are the exponential function:
and the exponential squared function:
wherev0anda0are parameters determining how fast the force increases.
The double exponential function has been used to fit the force as a function of distancedbetween the magnets and the sample[15].In this study,for simplicity,we suppose that the force in magnetic tweezers is an exponential functionF(d)=200 exp (-3d)pN,withdin units of millimeters[figure 1].
2.3.Simulation to obtain unfolding force distribution P(F)
Given the known force-dependent unfolding rateku(F) of a protein and the force-loading functionF(t),the unfolding process can be simulated using a Monte Carlo simulator[19].The initial state of the protein is its native state N.The entire simulation process is coarse-grained into a random event chain with a time interval of Δtper frame.The probability of the protein unfolding in each frame isku(F)Δt.When the protein molecule unfolds,the simulation stops,and the unfolding force is recorded.The unfolding force distributionP(F)can be obtained by the statistical histogram of unfolding forces from multiple repeated simulations.
2.4.Relationship between F(t),ku(F) and P(F)
From the knownku(F) andF(t),P(F) can also be derived analytically or numerically.Since the initial state is native state N,the survival probability of N stateS(t) obeys the differential equation:
with initial conditionS(0)=1,and
Therefore,P(F) is given by equation:
In single-molecule manipulation experiments,we controlF(t) and measureP(F),and analyze the data to obtainku(F)with equation [23]:
The unfolding force distribution is usually obtained as discrete values from a statistical histogram.The Dudko–Hummer–Szabo equation elucidates the relationship between the histogram of the unfolding force andku(F) [20]:
In this study,derivations were performed usingWolfram Mathematica12.1 software for complex analytical calculations.
3.Results
3.1.Comparison of force distributions under linear and nonlinear force-loading
First,we study the force distributions of two kinds of nonlinear force-loading,exponential function and exponential squared function,in comparison with that of linear forceloading with a constant loading rate.We set the force-loading curves of the exponential function with parametersF0=1 pN andv0=0.7 s-1,exponential squared function with parametersF0=1 pN anda0=0.06 s-2,and linear function with parametersF0=1 pN andr=8 pN·s-1[figure 2(c)].The parameters are set to have unfolding forces at similar values,under Bell’s model with default parameters.It was observed that,compared to the linear force-loading,the exponential and exponential squared functions spend more time at lower forces and reach a faster instantaneous loading rate at higher forces.
We calculated the velocity profile of magnetsvmag(t)[figure 2(a)],and the trajectory of magnetsdmag(t)[figure 2(b)] in the MT setup for these three types ofF(t).Under linear force-loading,the magnets move with drastically changing velocity,especially with high velocity and high acceleration at lower forces.The motion of the magnets under the exponential force-loading is slower with constant velocity.Under the exponential squared force-loading,the magnets move with constant acceleration.Therefore,the exponential force-loading offers a more user-friendly control,requiring only motion with uniform velocity.
Furthermore,we examined the unfolding force distributionsP(F) under these three types of force-loading.We derived the formula forP(F) and performed numerical calculations [figures 3(a)–(c)].Based on equation (5),the unfolding force distribution for the linear force-loading function (2) is given by,
The unfolding force distribution for the exponential force function (3) is given by,
where Ei(x) represents the exponential integral function:
For the exponential squared force function,we cannot derive the analytical formula of unfolding force distribution,while the numerical solution can be obtained.

Figure 2. Linear force-loading and two nonlinear force-loading schemes.The plots illustrate the linear force-loading Flinear(t)=1+8t (in black)with a constant loading rate of 8 pN·s-1,the exponential force-loading function Fexp(t)=exp (0.7t)pN(in red)and the exponential squared force-loading function Fexp2(t)=exp (0.06t2)pN (in blue).The velocity of magnets (a),the distance between the magnets and the sample (b),and force (c) are shown as functions of time for three types of force-loading schemes.
We conducted numerical calculations of the probability density of unfolding force for different parameters.For each of the three force functions,three sets of parameters were used to calculate unfolding force distributionsP(F)[figures 3(a)–(c)].The parameters for the red curve are the same as in figure 2.
Under linear force-loading,it was observed that the shape ofP(F) remains essentially the same across different loading rates,with the most probable unfolding forceincreasing with the loading rate [figure 3(a)].Similarly,for both exponential and exponential squared force functions,the most probable unfolding forcesincrease with the parametersv0ora0[figures 3(b) and (c)].
For the linear force-loading,the Bell–Evans formula provides the relationship between the most probable unfolding forceand the loading rater[13]:
which gives:
We computed the relationship between the most probable unfolding forceand the force-loading parameterv0under Bell’s model for the exponential force function:
whose solution is expressed with a LambertWfunctionWk(z)[24]:

Figure 3. The unfolding force distribution for linear force-loading and two nonlinear force-loading schemes following Bell’s model.(a)The unfolding force distributions under linear force-loading with constant loading rates r=0.8 (black),8 (red) and 80 (blue) pN·s-1.(b) The unfolding force distributions for the exponential force-loading function with parameters v0=0.07(black),0.7(red)and 7(blue)s-1.(c)The unfolding force distributions for the exponential squared force-loading function with parameters a0=0.006(black),0.06(red)and 0.6(blue)s-2.(d) The relationship between the most probable force and loading rate r under linear force-loading.The square dots are derived from the numerical data in figure(a),and the black line represents the theoretical relationship.(e)The relationship between the most probable force and parameter v0 for the exponential force-loading.The square dots are derived from numerical data in (b),and the black line represents the theoretical relationship.(f) The relationship between the most probable force and parameter a0 for the exponential squared force-loading.The square dots are derived from numerical data in (c).
When dealing exclusively with real numbers,it suffices to considerW-1andW0.Here,W-1corresponds to the maxima in the unfolding force distribution profile,whileW0corresponds to the minima.According to the probability distribution[figure 3(b)],the smaller solutionW0corresponds to a local minimum of the probability distribution function,consistent with the upward trend in probability at lower forces observed in the exponential force-loading.
We plotted the analytical relationships [figures 3(d)–(f)]of the most probable forceF*with the force-loading parameters (equations (12) and (14)) and compared them with specific points of the most probable force derived from the numerical probability distributionP(F)[figures 3(a)–(c)].It is concluded thatF*derived numerically for the linear forceloading and exponential force-loading curves are consistent with the predictions of analytical equations (12) and (14)[figures 3(d)–(e)].
For the case of an exponential squared force-loading,the unfolding probability distributionPexp2(F) resists simplification,and the most probable unfolding forceis challenging to calculate.Although no specific analytical expression has been derived,the scatter plot from the numerical method suggests thatis also approximately a linear function of the logarithm ofa0.
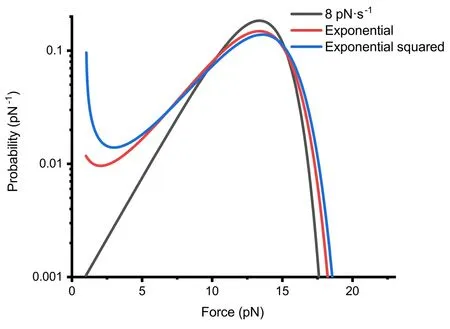
Figure 4. Under Bell’s model,when the forces involved in protein unfolding events are approximately similar,we present a comparative graph of the theoretical probability density P(F)distributions for unfolding events under linear,exponential and exponential squared force-loading.The specific force functions are Flinear(t)=1+8t (in black), Fexp(t)=exp (0.7t)pN (in red) and Fexp2(t)=exp (0.06t2)pN (in blue).The three curves in the graph represent the numerical solutions for the theoretical probability density P(F),calculated using these three force curves F(t) and typical protein molecular properties,with 1000 equidistant numerical solutions for each curve.
At lower forces,both the exponential and exponential squared force functions show more unfolding events,especially the exponential squared force-loading,which exhibits a pronounced upward trend at very low forces.This phenomenon is more evident when the force-loading parameters (v0ora0) are small,which is related to the longer duration these functions spend at lower forces.
3.2.Practicality comparison of exponential force functions
Our focus was directed towards the study of exponential force functions,due to their ease of implementation in magnetic tweezers setups.We compared the unfolding events obtained under constant loading rate,exponential loading and exponential squared loading conditions [figure 4].The force curves for these three conditions are as shown in figure 2(c).The peak distributions of unfolding events for all three forceloading functions are closely aligned (around 14 pN).At lower forces,the exponential and exponential squared functions exhibit more unfolding events,especially the exponential squared function,which shows a pronounced upward trend at very low forces.The upward trend observed in the probability density curves is not always present.Through analytical derivation,we found that under the exponential force-loading,the occurrence of a local minimum requires the exponential function parameterF0to be sufficiently small(preferably less than 1/βxu),andv0to satisfy the inequalityv0>k0e2.Moreover,the probability density curves for the exponential and exponential squared force-loading functions appear flatter.For example,the probability at 2.5 pN differs by approximately a factor of 10.Under the exponential function,the magnets in our setup required only a uniform motion and remained at low speeds over an extended period [figure 2(a)],offering mechanical stability far surpassing that under the constant loading rate.Thus,the exponential force-loading function not only facilitates easier implementation in experimental setups but also fully meets the requirements for standard measurements of protein unfolding events.
3.3.Derivation of F(t) to generate uniform P(F)
According to the Dudko–Hummer–Szabo equation,ku(F)can be obtained in the force range with a non-zero histogram,and the relative error depends on the counts of unfolding events in each bin.Therefore,we raise the question:what kind of forceloading function can generate a uniformly distributedF?With uniformly distributedF,the rate of change of survival probability is proportional to the rate of change ofF:
whereC0is a proportionality constant,and
Combining equations (1),(15) and (16),we derived the following relationship:
wheret(F) is the inverse function ofF(t),andF0andt0are constants of integration that incorporate the constantC0and the force range with uniform distribution [Appendix].
Directly deriving the expression forF(t) is challenging.Therefore,F(t) is obtained using the numerical method.The exponential integral Ei(x) diverges asx→0,and its inverse function has multiple-value regions.Consequently,F(t) theoretically possesses two distinct solutions satisfying the equation;one solution ofF1(t) increases with time,while the other solutionF2(t) decreases with time [figure 5(a)].
Having obtainedF1(t) andF2(t) force curves that can uniformly distribute the unfolding force within the range of 1–21 pN through equation(17),we tested the unfolding force distributions of protein under this force-loading via Monte Carlo simulation [figures 5(b)–(c)],which are significantly flatter than the unfolding force distributions under linear force-loading[figure 5(d)].UnderF1(t)orF2(t)force-loading,the unfolding force distributions cover our range of interest(1–21 pN)and are nearly flat,fulfilling the initial assumption.
InF1(t) orF2(t) force-loading curves,the absolute value of the slope is exceptionally high,specifically during the late phase of the monotonically increasing curveF1(t) and the early phases of the monotonically decreasing curveF2(t)[figure 5(a)].Insufficient density of sampling data points in single-molecule manipulation experiment setups can lead to significant precision loss.Under the monotonically decreasingF2(t)force-loading,there is a steeper slope at the beginning of the experiment and a more extended duration of low force at the end of the experiment.In addition,starting from a high force is not easy to control in magnetic tweezers experiments.Therefore,onlyF1(t) might be practical in real experiments.

Figure 5. Visualization of the force curves for force-loading F1/2(t)that can uniformly distribute the unfolding force and linear force-loading.Histogram of simulated unfolding events with respect to force under these conditions.(a)The force curves observed in the range of 1–21 pN generated by proteins with typical attributes.The red and blue curves represent monotonically increasing and decreasing forces,respectively,generated using the inverse function of equation (17).Black curve represents the traditional constant force-loading of 8 pN·s-1.(b)Histogram of unfolding force under F1(t) force-loading,simulated with a Monte Carlo model based on Bell’s model for protein unfolding rates.Simulation,divided into ten groups of 500 force-application experiments each,presents the average (histogram height) and standard deviation (error bars) across these groups.(c) Similar to the above,but tested under the condition of F2(t) force-loading.(d) Similar to the above,but tested under the condition of a constant force-loading of 8 pN·s-1.
4.Summary and discussion
Theoretically,the force-loading functionF(t),forcedependent transition rateku(F) and unfolding force distributionP(F) are interdependent.With two of them known,the third can be obtained.In single-molecule manipulation experiments,we setF(t),measureP(F) and analyze the data to obtainku(F).
In traditional single-molecule manipulation experiments,linear force-loading with a constant loading rate is the most popular approach.Constant force measurement can be considered as zero loading rate,which gives the transition rate at a specific force.In this study,we have explored several typical nonlinear force-loading methods.The force of magnetic tweezers is almost an exponential function of the distance between the magnets and the sample.Consequently,we analyzed the distribution of protein unfolding forces under exponential and exponential squared force-loading functions,corresponding to the movements of magnets with constant velocity and constant acceleration,respectively.We found that the obtained force distribution is broader compared to constant loading rate measurements,providing unfolding rates across a larger force range.
We found that exponential force-loading provides an additional advantage when it is used in magnetic tweezers.Under similar forces,the motion of the magnet using exponential force-loading involves slower velocities and smaller accelerations compared to the constant loading rate.This offers greater mechanical stability for the experimental apparatus.On the other hand,with the same limitation of velocity and acceleration,exponential force-loading can cover a larger range of dynamic measurements,which is important since it reveals the more detailed free-energy landscape of biomolecules.
In addition,we have conducted theoretical analyses with the premise of uniformly distributed unfolding force across a certain force range.We have derived the force functionF(t)under Bell’s model to meet this expectation.Surprisingly,we discovered a force curve that decreases monotonically over time and also meets our expectation of uniform force distribution.Although it might be not very practical in experiments since we do not knowku(F) in advance,as the first trial to derive force functionF(t) with knownku(F) andP(F),this demonstrates that there are two solutions ofF(t)that both satisfy the requirements.
In magnetic tweezers experiments,the extension of molecule is obtained from the position of the magnetic bead.When the fluctuation of the extension is much smaller than the unfolding step size,the unfolding event can be identified accurately.Force is only determined by the distance between the permanent magnets and the sample.Therefore,the uncertainty of unfolding force is affected by the synchronization of the camera and the position reading of the motorized stage that moves magnets in the setup.Fortunately,the uncertainty of the unfolding force for each unfolding event is usually much smaller than the distribution range of the unfolding forces.Therefore,noise of both force and extension will not affect the application of our theoretical results in magnetic tweezers experiments.
Acknowledgments
This research project was supported by the National Natural Science Foundation of China (Grant Nos.12174322 to HC,12204124 to ZG,32271367 and 12204389 to SL),the 111 project (Grant No.B16029) and the Research Fund of Wenzhou Institute.
Appendix: Derivation of nonlinear F(t) for uniform P(F) under Bell’s model
This section gives the derivation procedures of equation(17).With uniformP(F),equation (15) and the following two equations:
are equivalent,whereF0,C1andC2are constants of integration.These equations essentially state thatS(t)andF(t)are linearly related at any time.By inserting equation (A1) into Bell’s model (1),we get:
whereC3is a constant of integration.After transformation,we obtain:
Let us define:
Substituting equation (A4) into equation (A3) yields:
Moreover,considering the expression for Ei (equation (10)),we can determine that,
Thus,it can be concluded that,
Integrating both sides results in the following:
whereC4is a constant of integration.After simplification,we have:
whereC5is another constant of integration.Substituting with equation (A4),we obtain:
After further simplification,we obtain equation (17).
 Communications in Theoretical Physics2024年4期
Communications in Theoretical Physics2024年4期
- Communications in Theoretical Physics的其它文章
- Exploring dielectric phenomena in sulflowerlike nanostructures via Monte Carlo technique
- Electrical characteristics of a fractionalorder 3 × n Fan network
- Diffusion of nanochannel-confined knot along a tensioned polymer*
- Two-component dimers of ultracold atoms with center-of-mass-momentum dependent interactions
- Phase structures and critical behavior of rational non-linear electrodynamics Anti de Sitter black holes in Rastall gravity
- Holographic dark energy in non-conserved gravity theory
