基于AMASPGD算法的FSOC系统波前畸变校正及性能分析

赵 辉, 于林仙, 秦玉林, 付英印, 李俊男

(1.重庆邮电大学通信与信息工程学院,重庆 400000; 2.信号与信息处理重庆市重点实验室,重庆 400000)

0 引言

自由空间光通信(FSOC)具有保密性强、传输速率快和传输容量大等优势[1-4]。然而,相干自由空间光通信(CFSOC)在中继距离、灵敏度和接收选择性方面均优于传统FSOC[5]。目前,光通信在商业、民用以及军事等领域均有所应用,例如在军事方面,普通的无线电卫星通信已经无法满足未来战争中海量数据传输压力,以及对于数据安全的考虑,相干FSOC的高安全性是未来军事安全方面的重要保证。但是大气湍流扰动会引起接收端光信号的波前畸变,这会显著降低相干FSOC系统性能。研究表明,自适应光学(AO)技术可有效减小大气扰动对自由空间光通信系统传输特性的影响。由于工作原理的缺陷,传统AO系统在高闪烁或低光功率的情况下很难达到足够的精度[6-7]。因此,基于盲优化搜索算法的无传感器自适应光学(SLAO)技术被提出。SLAO系统根据获得的图像自动调整相干FSOC系统的性能指标,因此该技术不需要波前重建[8]。

尽管针对SLAO系统已经提出了很多算法,随机并行梯度下降(SPGD)算法因其简单、成熟、复杂参数少等优点,在SLAO系统中仍被频繁采用[9]。遗憾的是,SPGD算法收敛速度慢,在迭代过程中容易陷入局部极值[10]。近年来,研究人员尝试了一些技术来改进SPGD算法并解决上述问题。动量随机并行梯度下降(MSPGD)算法是YANG等[11]将传统动量与SPGD算法相结合而产生的,该算法不仅加快了迭代速度,而且保证了相干合成过程的稳定性,然而,该方法没有考虑局部极值;HU等[12]利用Adam优化器将SPGD算法进行优化,并提出了自适应随机并行梯度下降(ASPGD)算法,提高了光纤耦合的性能;2022年,ZHANG等[6]利用ASPGD算法对波前畸变进行了校正,降低了相干FSOC系统的误码率(BER),然而,该方法的性能没有在更强的湍流下进行分析。另外,近年人工智能技术也被用于波前畸变校正,如2021年CHEN等[13]将卷积神经网络技术用于波前畸变校正提升了校正速度。总之,上述大多数算法都是为了解决特定的光学问题而设计的,并且这些增强算法仍存在性能指标受限、稳定性差、无法自适应调整参数等问题。因此,希望设计一种算法,通过改善这些缺陷来提高相干FSOC系统的性能。

动量算法最初被提出用于训练深度学习中的人工神经网络,它可以显著提高收敛速度。受MSPGD算法和ASPGD算法的启发,将聚合动量(AM)[14]与自适应矩边界(AdaMod)优化器[15]及SPGD算法相结合,提出了一种增强型SPGD算法——聚合动量和自适应矩边界加速随机并行梯度下降(AMASPGD)算法。此外,利用相干通信理论分析了相干FSOC系统的混频效率(ME)和BER。最后,通过数值仿真分析了算法的波前校正效果。

1 系统模型与基本原理

1.1 相干FSOC系统模型

图1为相干FSOC的系统框图。

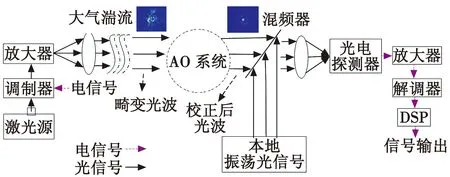
图1 相干FSOC系统框图Fig.1 Block diagram of coherent FSOC system

由图1可知,光信号在自由空间中传输时会受到大气湍流干扰,在接收器之前有一个用于校正波前像差的SLAO系统,光信号由本地振荡光信号在接收端相干探测和接收。然后,光信号通过光电探测器转换为电信号,最后,通过解调和数字处理输出数据信息。激光信号为ES(t)=AScos(ωSt+φS),本地振荡光信号为ELO(t)=ALOcos(ωLOt+φLO),其中,AS和ALO分别表示光信号和本地振荡光信号的振幅,φS和φLO分别表示它们的相位,ωS和ωLO分别表示它们的角频率。

SLAO系统如图2所示。

图2 无传感器的自适应光学系统Fig.2 Sensor less adaptive optical system

由图2可知,CCD相机将接收的远场光斑图像传入计算机,计算机利用控制算法进行迭代并计算出使远场光斑图的某一性能指标达到最大值时的控制电压,并将此驱动电压输入至变形镜(DM)驱动DM进行畸变像差校正。其中,φ(r,θ)为初始畸变相位,ψ(r,θ)为DM产生的补偿相差,Φ(r,θ)为补偿后的残余相差。

1.2 DM模型

本文实验中使用的波前校正器为36单元连续变形镜[16],DM的影响函数服从高斯分布,第i个驱动器在DM坐标(x,y)处的镜面影响函数表示为[17]

(1)

式中:xi和yi分别表示变形镜中第i个驱动器的横纵坐标;参数α为高斯函数指数;d为驱动器的归一化间距;ω为相邻驱动器之间的交联值。在DM所有驱动器的作用下,变形镜发生形变并生成补偿相位表示为[18]

(2)

式中,ui为施加给第i个驱动器的电压。

1.3 Zernike多项式及畸变相位的产生

在SLAO系统中,通常采用一系列Zernike多项式[19]的线性组合来表示湍流导致的激光信号波前畸变相位φ(r,θ),表达式为[18]

(3)

式中:(r,θ)为单位圆内的极坐标;M为Zernike多项式阶数;Zi(r,θ)和ai分别为第i阶Zernike多项式及其系数。本文选择满足Kolmogorov理论的前65阶Zernike多项式拟合不同湍流强度下的畸变波前。

1.4 相干FSOC理论基础

混频效率(ME)是评价相干自由空间光通信系统有效性的重要参数,ME综合反映了激光载波信号受到大气湍流、空间传输等因素的影响。而在使用零差探测的相干FSOC系统中,实际工程应用时通常将ME约等为远场焦平面图像的斯特列尔比(SR)[20],SR是指实际峰值强度与衍射极限峰值强度的比值,该近似关系可用于实验中获得相干FSOC系统中ME的变化规律,并且,SR与波前像差的均方根(RMS)的近似关系表示为[16]

(4)

对于采用二进制相移键控(BPSK)调制的受大气湍流干扰的相干FSOC接收系统,BER为[21]

(5)

式中:erfc(·)为互补误差函数;δ为光电探测器的量子效率;NP为接收端的单比特光子数;参数η表示ME。

2 基于AM和AdaMod优化器的增强型SPGD(AMASPGD)算法

本文将介绍SPGD算法如何控制和更新DM的电压,说明算法控制单元的工作过程,并详细介绍AMASPGD算法。

2.1 SPGD算法

本文采用SR作为优化算法的性能指标J,SLAO系统中SPGD算法校正波前像差的步骤如下:

1) 为DM上的K个驱动器设置初始电压u=(u1,u2,…,uK),同时设定增益系数λ的初始值和算法的总迭代次数N;

2 ) 产生随机扰动电压δu=(δu1,δu2,…,δuK);

3 ) 将正向扰动电压和负向扰动电压施加于DM的驱动器上,分别计算和更新正负扰动性能指标J+=J(u+δu)和J-=J(u-δu),再通过δJ=J+-J-计算性能指标的变化量;

5) 重复步骤2)～4),直到迭代次数完成或满足预设条件。

2.2 AMASPGD算法

为了解决SPGD算法无法自适应调整增益率、收敛速度慢和易陷入局部极值等问题,HU等[12]提出了ASPGD算法,该算法的核心是使用一阶动量和二阶动量提高了收敛速度并实现了增益系数的自适应调整,即

(6)

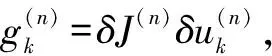
(7)

最终,ASPGD算法更新变形镜的控制电压方程为

(8)

式中,ε用于避免数值问题,通常取值10-8。

本文利用AM和深度学习中的AdaMod优化器提出AMASPGD算法以校正波前像差,进一步提升SPGD和ASPGD算法的畸变波前校正性能。聚合动量是经典动量的变体,它由多个具有衰减率控制参数β(i)的速度矢量进行线性组合,并在参数更新时对速度矢量进行平均。具体来说,将AM和AdaMod优化器集成于传统的SPGD算法的整个优化过程如下。

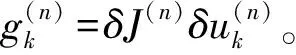
(9)

(10)

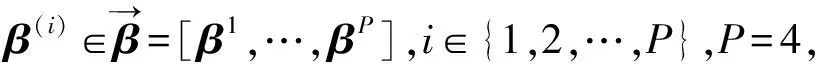
(11)

(12)

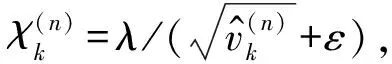
(13)

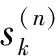
(14)

(15)

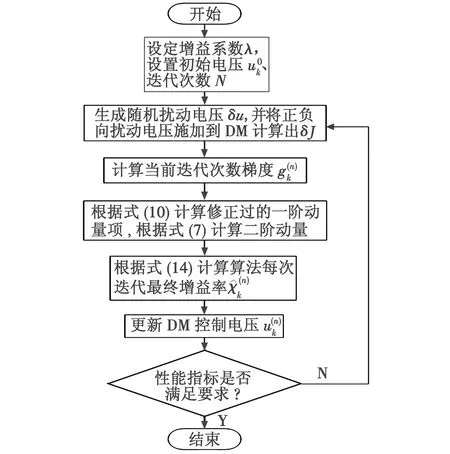
图3 AMASPGD算法流程图Fig.3 Flow chart of AMASPGD algorithm

3 仿真实验与分析

3.1 参数设置

基于36个驱动器的DM相关参数α、d和ω分别赋值为2、0.3和0.36。此外,为了便于描述算法在不同湍流强度下的校正效果,将湍流强度大小量化为D/r0,数值越大代表湍流越强[22],D和r0分别代表接收端望远镜直径和大气相干长度。通过大量实验,最终确定各种算法在不同湍流强度下的最优增益系数,如表1所示。此外,设定量子效率δ=1[6],单比特光子数Np=18。

表1 不同湍流强度下各算法的最佳增益系数

3.2 校正效果及分析

本文分析了AMASPGD算法对波前畸变相位校正的结果,首先,给出了如图4所示的AMASPGD算法校正的波前相位和远场光斑图。另外,为了验证所提算法的有效性和优越性,并与现存的3种算法进行了比较。同时,为了减小算法固有随机性的影响,每种算法对每个波前畸变相位进行30次校正,并对30次校正结果曲线进行平均,然后将4种算法的平均校正效果曲线进行比较和分析,结果如表2、图5和图6所示。

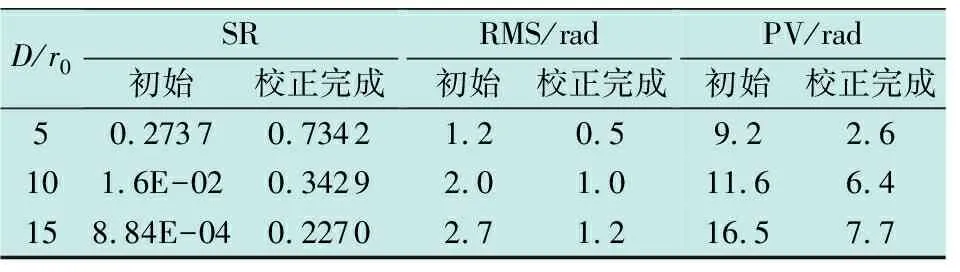
表2 AMASPGD算法校正波前畸变前后的SR、RMS和PV值

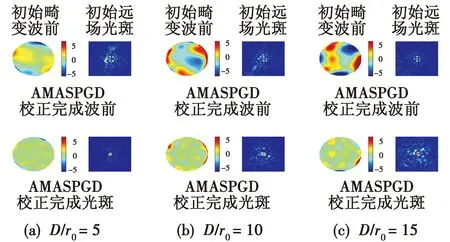
图4 AMASPGD算法校正的波前相位和远场光斑图

图5 不同湍流强度下4种算法的ME变化曲线

图6 不同湍流强度下4种算法的误码率变化曲线图

图4中,校正前3种湍流强度下产生的波前相位均存在明显像差,对应的远场光斑图中光斑较为分散。在D/r0=5湍流强度下的波前畸变经过AMASPGD算法校正后,远场光斑质心向中心收敛,周围散斑明显减少,波前相位表面颜色接近均匀。波前相位在D/r0=10和D/r0=15湍流强度下的严重畸变也得到显著校正,除边缘仍存在少量的高低频成分外,波前相位的表面颜色近乎均匀。同时,远场图像中能量更加集中,SR分别提升至0.3429和0.2270。从表2中可以发现,波前畸变经过AMASPGD算法校正后的PV值和RMS值均有明显减小。以上分析表明,所提AMASPGD算法能够有效校正不同湍流强度下导致的波前畸变。

图5为AMASPGD算法与另外3种现存算法在校正波前畸变时的ME曲线变化对比图。将曲线即将接近平滑的拐点定义为阈值,并选取0.71、0.32、0.22作为不同湍流强度下的收敛阈值,且在图5中给出了各算法达到阈值时的迭代次数,即170、199、202、213、209、294、262、314、270、403。

由图5(a)可知,各算法对弱湍流引起的畸变均有较好的校正效果。当湍流强度D/r0=5时,AMASPGD算法收敛最快,在第170次迭代时达到阈值,收敛速度相比于MSPGD算法、ASPGD算法和SPGD算法分别提升了14.57%、15.84%和20.19%。尽管此时ASPGD算法的收敛速度明显快于SPGD算法,但ASPGD算法到达收敛阈值后会出现ME振荡现象进而降低了算法收敛精度。当湍流强度D/r0=10时,MSPGD算法、ASPGD算法和SPGD算法的迭代速度相比于AMASPGD算法分别慢28.91%、20.23%和33.44%。SPGD算法在D/r0=15的湍流强度下无法达到收敛点,因此在湍流强度D/r0=15的条件下,AMASPGD算法收敛速度相比于SPGD算法至少提高了55.00%。

图6为4种算法的误码率变化曲线图。

由图6(a)可知,SLAO系统补偿波前相位失真后BER性能得到了显着改善。采用AMASPGD算法补偿波前像差后,在3种湍流强度下系统的误码率性能分别提升了6、5和3个数量级。由图6(b)和图6(c)可知,随着湍流逐渐增强,SPGD算法和MSPGD算法在收敛速度和BER收敛值方面越来越差,甚至在湍流强度D/r0=15下SPGD算法和MSPGD算法直到迭代完成依然无法到达收敛点。

综上可知,校正不同湍流强度下波前畸变时,AM-ASPGD算法在保证较好的最终收敛极值的同时,收敛速度更快,稳定性更强。

3.3 随机扰动电压对算法的影响

随机扰动电压δu取值对基于梯度下降的算法有重要影响[6]。为了进行合理的仿真实验对比,在保持其他设置不变的情况下,在不同δu值下进行仿真对比,湍流强度选取D/r0=5。

如图7(b)所示,SPGD算法对δu的取值十分敏感。当δu为0.01时,SPGD算法几乎失去校正能力,当δu增加到0.5时才能实现有效校正。这说明当δu取值较小时,SPGD算法不能获得有效的校正效果,但当δu取值到达一定值时,SPGD算法能正常工作。相反,δu的变化对AMASPGD算法的校正性能几乎没有影响,其3条ME校正曲线几乎重合。因此,该结果表明,AMASPGD算法在较大的δu范围内具有一定的鲁棒性,便于SLAO系统的实际应用。

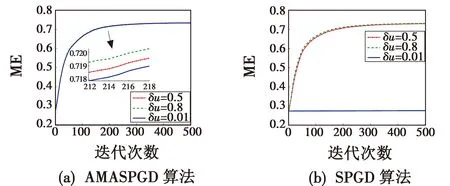
图7 不同δu值下AMASPGD和SPGD算法鲁棒性的比较

4 结论

SPGD算法被广泛应用于波前畸变校正,但是该算法存在收敛速度慢,无法自适应调整增益率的缺陷,研究人员一直在尝试改进SPGD算法进而得到更加高效可靠的方法。本文提出了一种基于AM和AdaMod优化器的改进SPGD算法。数值仿真表明,所提AMASPGD算法有效降低了波前畸变相位的PV值和RMS值,并且该算法对参数敏感性更低、鲁棒性更强,最终基于该算法的SLAO单元提高了相干FSOC系统的ME和BER性能,在3种湍流强度下系统的误码率性能分别提升了6、5和3个数量级。在校正速度方面,在3种不同湍流强度下,AMASPGD算法相比于SPGD算法分别提高了20.19%、33.44%和55.00%。综上所述,AMASPGD算法用于波前畸变校正不仅加快了校正速度,而且提高了SLAO系统像差校正效果,进而提高了相干FSOC系统的传输性能。