基于刀齿轨迹模型的五轴侧铣加工铣削力预测*

桂 昊，张立强，杨青平

（1.上海工程技术大学，上海 201620；2.成都永峰科技有限公司，成都 610511）

对于航空航天薄壁件来说，切削力是影响铣削加工的重要物理因素，过大的切削力会使刀具与工件发生振动、变形，从而出现零件表面加工质量低下、刀具磨损加剧等现象。虽然通过降低切削参数来减小切削力可以提升零件质量，但是牺牲了加工效率。预测切削力是研究铣削加工的稳定性、受力变形偏差以及工艺参数优化的基础。

切削力模型建模方式主要有4种：物理模型[1]、经验模型[2]、神经网络模型[3]及机械力学模型[4]，其中机械力学模型应用最为广泛，而对于该类模型，瞬时切屑厚度对于切削力的预测至关重要。Martellotti等[5]通过分析平面中圆弧的运动几何，提出了圆柱铣刀的经典瞬时切屑厚度模型h=fzsinθ，其中fz为每齿进给量，θ为刀齿周向位置角，但是经典模型仅适用于三轴加工，五轴侧铣刀具姿态多变，刀具与工件的接触区域计算困难；Ferry[6]定义了各个刀具微元的进给坐标系，进而将经典三轴的瞬时切屑厚度计算公式推广到了五轴铣削中；王立平等[7]提出了一种五轴侧铣瞬时切屑厚度的拆分计算方法，通过判断刀具姿态补偿了经典切屑厚度模型；He等[8]提出了一种基于真实齿轨的五轴球头铣刀切削力新模型；董永亨等[9]通过齐次坐标系建立了刀齿的运动轨迹，并计算了当前刀齿与工件的边界交点，求出瞬时未变形切屑厚度；王博[10]结合球头铣刀切削刃的几何特点建立切削刃微元点的空间位置矢量，并进一步推导描述切削刃微元点轨迹的矢量形式。以上研究对五轴瞬时切屑厚度研究比较深入，但却忽略了刀具跳动的存在会影响瞬时切屑厚度值。Li等[11]考虑了刀具跳动的影响，提出一种近似圆弧轨迹模型来替代真实的摆线齿轨模型，圆形假设引入的近似误差在可以忽略的同时又提高了计算效率。Wang等[12]在切削力预测中探究了刀具跳动对刀齿运动轨迹的影响，并通过切削力试验进行了验证。

本文通过五轴侧铣几何运动学模型描述了五轴刀位在空间中的姿态，随后提出一种基于刀齿轨迹模型的切削力预测模型，计算当前切削刃上切削点到前几个刀齿回转圆柱面的映射距离，并在坐标变换关系下，将空间中的线面求交计算转换成二维平面的线与圆弧的求交运算。在考虑刀具跳动对圆弧轨迹的影响后，求解方程组获得切削微元的瞬时切屑厚度值，最后在五轴机床上进行了加工试验，验证了本文所建立模型的有效性。

1 侧铣几何运动学模型

五轴侧铣过程的刀具姿态变化复杂，在研究力学模型之前，首先建立几何运动学模型。如图1所示，每个刀位点信息包括刀尖点坐标Pi与刀轴矢量Ti，在刀位[Pi，Ti]向刀位[Pi+1，Ti+1]运动过程中，需要计算t时刻的刀位点Pt和刀轴矢量Tt，CNC系统在执行刀位文件时，两相邻刀位间的运动为线性插补运动，刀位点Pt计算公式表示为

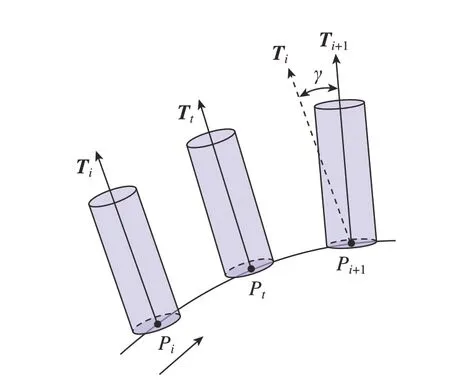
图1 刀具位置插补示意图Fig.1 Schematic diagram of tool position interpolation

式中，fz为每齿进给量；n为主轴转速；N为刀具齿数；dP1，P2为刀位点P1和刀位点P2之间的距离。

两相邻刀位点刀轴矢量Ti与Ti+1间的夹角γ计算公式为

已知刀位[Pi，Ti]向刀位[Pi+1，Ti+1]运动的刀轴矢量夹角γ，在t时刻刀轴矢量计算公式为

Rot（v，θ）·Ti为向量Ti绕向量v顺时针旋转角度θ，若矢量v=[vi，vj，vk]，则Rot（v，θ）·Ti计算公式[13]为

式中，versθ= 1- cosθ。

为准确描述五轴侧铣的复杂空间运动，分别建立了工件坐标系、刀具坐标系、局部刀齿坐标系。首先建立固定不动的工件坐标系OWXWYWZW，刀具姿态和工件均在工件坐标系下表示。如图2所示，在工件坐标系下，刀具侧刃沿着两条引导线滑动形成扫掠面，在这个过程中，以刀尖PC=[Pcx，Pcy，Pcz]为原点建立刀具坐标系OCXCYCZC。

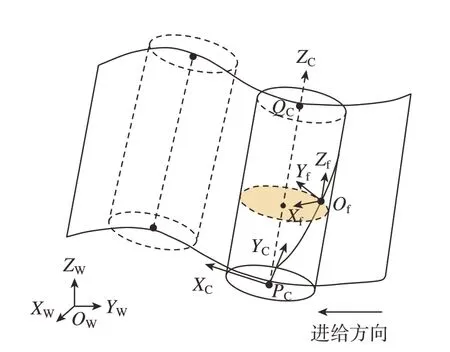
图2 坐标系建立示意图Fig.2 Schematic diagram of coordinate system establishment

XC=[Xcx，Xcy，Xcz]指向当前刀位进给方向，ZC=[Zcx，Zcy，Zcz]为刀轴矢量T。建立刀齿微元坐标系OfXfYfZf，其轴方向矢量Zf与刀具坐标系ZC轴同向，Xf轴为过点Of指向刀具中心线方向。由于存在螺旋角β，刀齿会随着轴向位置变化而出现变化的滞后角φ。已知半径R、轴向高度z，滞后角可以表示为

设刀具底端切削刃的旋转角为ϕ，齿数为N，则在刀具高度z处第j个刀齿的旋转角表示为

在刀具坐标系下，高度z处第j个刀齿的切削点的坐标可以表示为

由于工件坐标系OWXWYWZW固定不动，而刀具坐标系OCXCYCZC会随刀具姿态的变化而变化，将变化的刀具坐标系转换到固定不动的工件系下表示，已知刀具坐标系XC、YC、ZC3个轴矢量，刀具坐标系转换到工件坐标的旋转矩阵可以由表示。PC为刀具坐标系的原点坐标，则将刀具坐标系转换到工件坐标系中的转换矩阵可以表示为

2 切削力模型

2.1 切削力计算

采用机械力学模型计算切削力，如图3所示，将刀具沿刀轴方向划分为M个厚度相等的切削微元盘。

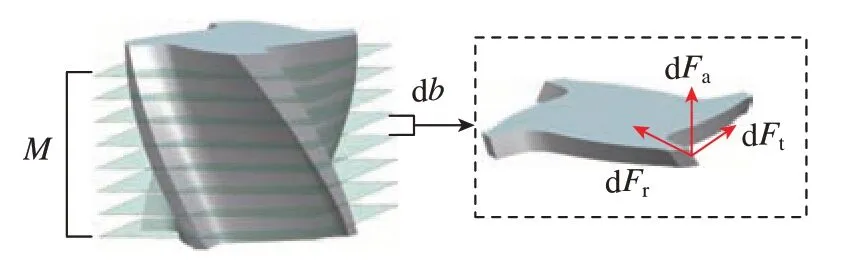
图3 切削力微元模型Fig.3 Micro-element model of cutting force

在刀具旋转角度为θi，j时，作用在第j个齿第i个切削微圆盘的切削力公式表示为

式中，Ktc、Krc、Kac分别为切向、径向和轴向剪切力系数；Kte、Kre、Kae分别为切向、径向和轴向犁切力系数；hi，j（t）为第j个齿第i个切削微圆盘的瞬时切屑厚度；db为切削微圆盘厚度；W（θi，j（t））是判断切削微圆盘是否参与切削的窗口函数，可以表示为

式中，θen，i，j、θex，i，j分别为第j个齿第i个切削微圆盘的切入角、切出角。

在t时刻，作用在工件上的总切削力分力可以通过将作用在轴向切削深度内的圆盘元件上的3个切削力相加和坐标变换得到，表示为

式中，Ti，j绕刀轴的旋转矩阵表示为

2.2 瞬时切屑厚度计算

瞬时切屑厚度为在刀具工件啮合区域内，当前刀齿的任意切削点沿刀齿面法向到已加工面的距离。如图4所示，前一刀齿回转面为已加工面，在切入角、切出角限制的接触区域内，有效瞬时切屑厚度为当前刀齿回转面与前一刀齿回转面相交的实体部分。

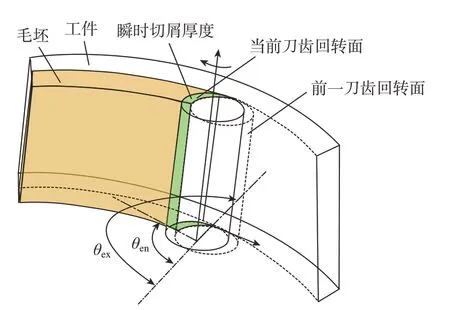
图4 瞬时切屑厚度模型Fig.4 Instantaneous chip thickness model

为计算瞬时切屑厚度，如图5所示，刀位M为前一刀位点，刀位N为当前刀位点，刀具在作平移和旋转运动时形成了瞬时切屑厚度h；Ai，j为刀具在刀位点N上第j个刀齿第i个切削微圆盘的切削点，计算点Ai，j到刀位M处的刀齿回转面的距离为点Ai，j处的瞬时切屑厚度。

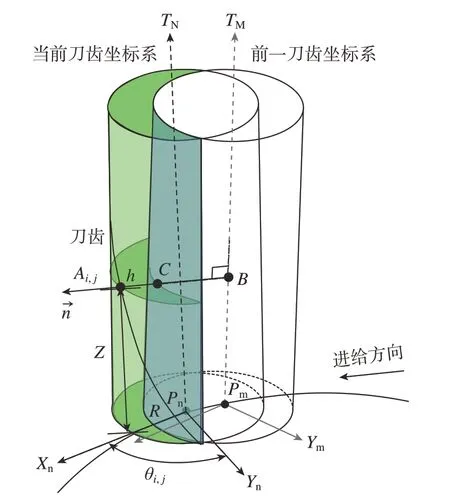
图5 瞬时切屑厚度计算示意图Fig.5 Instantaneous chip thickness calculation

首先建立刀位M的刀具坐标系OMXMYMZM以及刀位N的刀具坐标系ONXNYNZN。切削点Ai，j处的切屑厚度h满足

式中，CM、、分别为在OMXMYMZM坐标系下M位置处的刀齿回转面上的交点、M位置处的刀齿回转面法向矢量及N位置处的刀齿切削点。

向量n垂直于刀位M的轴线，是切削点Ai，j垂直于M位置处刀齿回转面的法向矢量；是刀具坐标系转换到工件坐标系的转换矩阵；Pn为坐标系原点。将点转换到工件坐标系下表示为

在坐标系OMXMYMZM下，刀位M处刀齿回转面的交点CM表示为

将式（20）～（22）代入式（15）求解方程组，得

交点CM的参数θ、z未知，联立方程消去θ简化计算为

法矢量与刀齿回转面有两个交点，所求解出未知数h的两个解中，最小h值为切削点到回转面有效切屑厚度值。

在实际加工过程中，刀具跳动不可避免，刀具跳动会改变瞬时切屑厚度的大小，从而使各齿的切削力峰值不同。如图6所示，定义刀具径向跳动偏移值为ρ，偏转角度为λ，则刀具跳动影响下的刀具半径为[12]

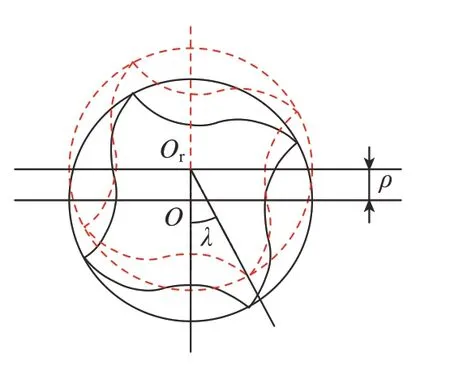
图6 刀具跳动示意图Fig.6 Schematic diagram of tool runout

若加工过程中受刀具跳动影响，当前切削点的瞬时切屑厚度不一定是到前一齿的刀齿回转面，而是到前k个刀齿回转面的距离。

依次计算当前切削点到前k个刀齿回转面的距离，最小值为当前切削点对应的真实的瞬时切屑厚度，即

3 切削力预测试验验证

为验证本文所提算法的有效性，在A摆头B转台的上海拓璞卧式数控机床HMC - C100PL上进行侧铣加工试验。毛坯材料为AL7050 - T7451，刀具为直径12 mm的整体硬质合金平底铣刀，切削刃数为3，螺旋角为45°，刀具跳动偏移值ρ为0.0017，偏转角度λ为42°。主轴转速2000 r/min、每齿进给量0.03 mm、切深10 mm、切宽1 mm，试验试件壁厚大于10 mm。试件的被加工面与刀位点如图7所示。

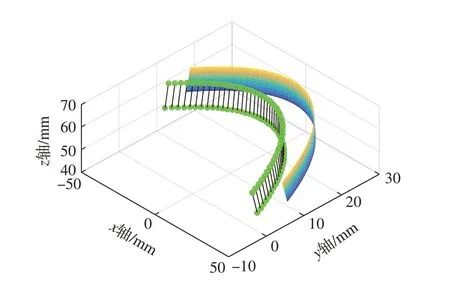
图7 MATLAB仿真加工曲面与刀位点Fig.7 Machining curved surface and cutter location by MATLAB simulation

切削力测量设备为Kistler 9272型四分量测力计，其x和y方向的灵敏度为- 7.8 pC/N，z方向的灵敏度为-3.5 pC/N，试验采样频率为10 kHz。数据采集设备为HR- CA- 411型电荷放大器、HRU1213MA型信号采集仪，试验设备如图8所示。

图8 切削力测量装置Fig.8 Cutting force measuring device

切削力系数标定采用文献[14]的方法，做5组槽铣试验，主轴转速2000 r/min、轴向切深1.5 mm，通过测力仪设备分别采集每齿进给量0.04 mm/r、0.06 mm/r、0.08 mm/r、0.10 mm/r、0.12 mm/r的槽铣切削力试验结果，获得平均切削力值，试验测量结果如表1所示。

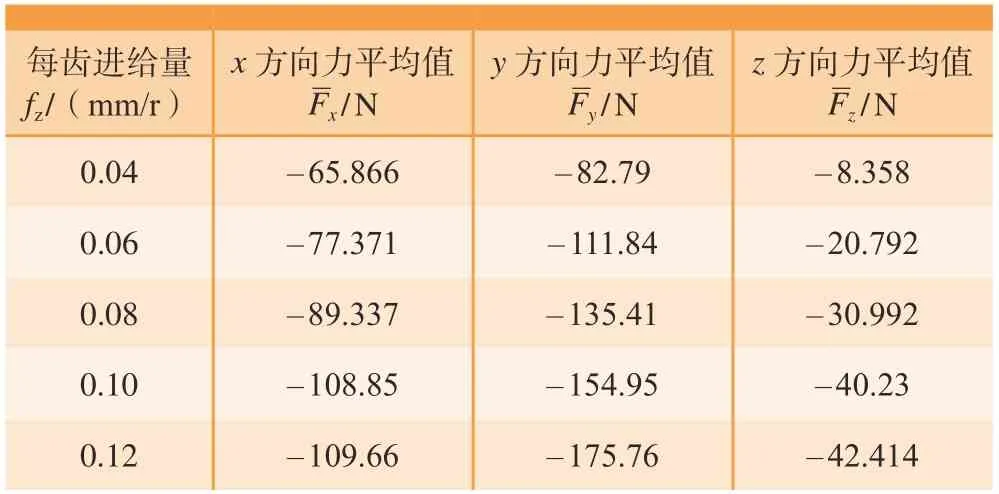
表1 不同进给的平均切削力值Table 1 Average cutting force at different feeds

用最小二乘法拟合实测切削力的平均值，如图9所示。

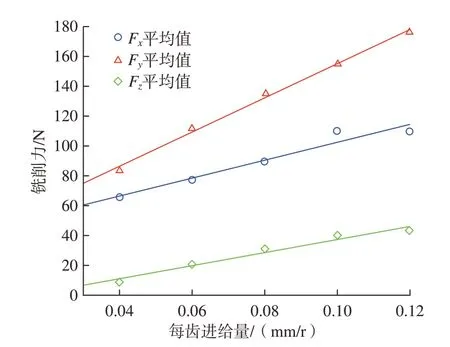
图9 最小二乘拟合切削力Fig.9 Least square fitting cutting force

拟合的切削力系数如表2所示。

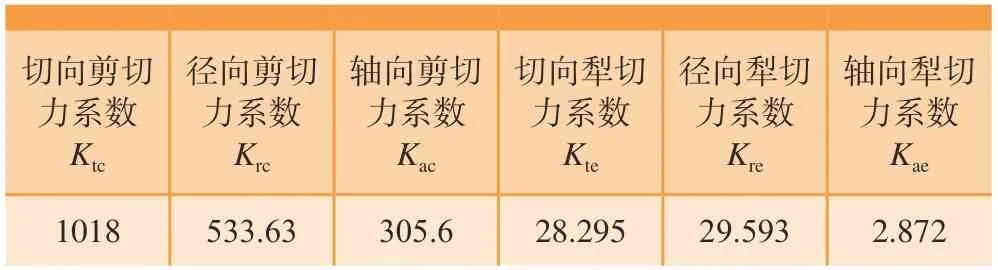
表2 切削力系数Table 2 Cutting force coefficient N/mm2

图10为刀具旋转一周期内测量与预测的结果对比图。测量结果与预测结果接近，预测的y轴切削力无论是趋势还是峰值都比较吻合；x轴切削力测量峰值与预测峰值相差较大，最大误差在24.5%左右，但整体趋势和实测值一致。在实际测量切削力值时，电荷放大器由于受潮及设备本身性能不稳定，测量的切削力值会发生漂移的情况，测量结果不可避免地会受到影响。

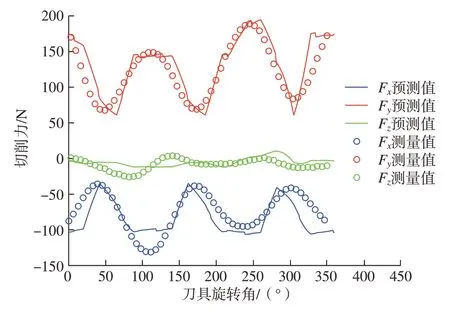
图10 刀具旋转一周期内切削力测量值与预测值比较Fig.10 Comparison of measured and predicted cutting force within one cycle of tool rotation

图11是工件在整个切削过程中切削力的预测值与实测值，可以发现，工件在x轴向受力减小的同时，y向受力在增大；从预测结果与实测结果来看趋势基本一致，但是切削力的轮廓线并未完全吻合，在侧铣过程中受刀具跳动影响，理论刀轴矢量与实际刀轴矢量会发生偏差，而刀轴矢量是识别刀具位姿的重要变量，这也会导致预测值与实测值出现偏差。

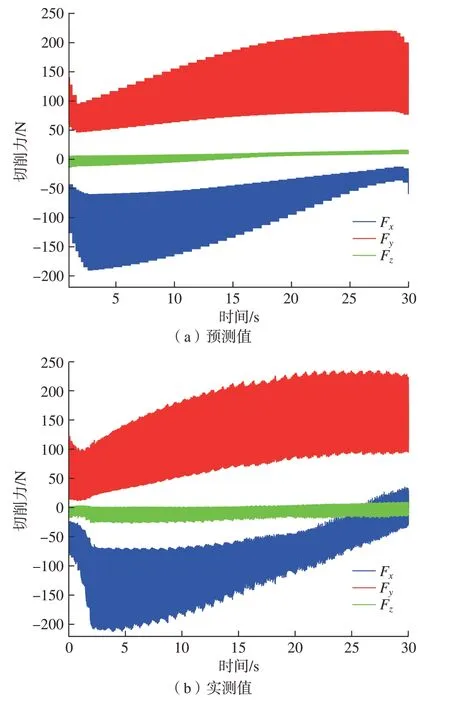
图11 工件整个切削过程切削力预测值和实测值Fig.11 Predicted and measured values of cutting force in the whole cutting process of the workpiece

4 结论

（1）以五轴侧铣几何模型表述了任意时刻的刀轴姿态，并建立了圆柱铣刀的刀齿运动模型，通过齐次坐标变换，把空间下的求交问题转换成平面中的求交解析计算。

（2）通过切削力标定试验获得切削力系数，仿真的x轴方向力增大的同时y轴方向的力在减小，最后将仿真的力值与实测力值进行比较，最大预测误差值在24.5%，从切削加工整个过程来看，切削力趋势和大小基本吻合，验证了本文模型用于预测切削力的有效性。

（3）在五轴侧铣加工过程中，航空航天类薄壁零件会因切削力作用出现让刀变形误差，且恒定的进给速度将严重影响五轴侧铣加工效率，基于本文的切削力预测模型可以进一步做薄壁件变形误差预测和进给速度优化等研究。