基于线性调频连续波的合作式通信辐射源测距

孙志国, 赵旭, 王震铎

(哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001)

飞机编队飞行除飞行表演等艺术效果外还有很重要的实战效果。而随着战机隐形化,一个合作式的隐蔽性强的通信辐射源测距系统越来越被需要,由于线性调频信号的时宽带宽积很大,隐蔽性很强,而且线性调频连续波测距系统具有极高的距离分辨率。本文基于线性调频连续波(linear frequency modulated continuous wave,LFMCW)信号设计了一种合作式通信辐射源测距系统。

基于LFMCW的合作式通信辐射源测距系统具有结构简单、精度高、功耗低、稳定性好等特点,在不考虑加速度时,线性调频连续波测距系统已经十分成熟,但加速度又是不可忽视的重要因素,当加速度存在时,经混频后的差拍信号的多普勒维频谱发生畸变,如果不对加速度进行估计,加速度小时会影响速度的估计性能,加速度较大时 甚至无法对速度进行估计,进而也会影响距离的估计性能。

在飞机编队的测距问题上,由于飞机速度、加速度都很大,一些先进战机速度可达几马赫,不得不考虑其对飞机编队测距系统的影响,加速运动目标,由于加速度的存在,混频后拍频信号的多普勒维被加速度调制成chirp信号[1-2],需要对其进行参数估计,进而估计出加速度,对加速运动目标的测距问题的难点在于对加速度及速度的估计问题,也即对chirp信号的参数估计问题。常见的chirp信号参数估计方法有压缩感知法[3]、分数阶傅里叶变换法(fractional Fourier transform,FrFt)[4]、基于压缩感知的离散分数阶变换法[5]、LVD(LV′s distribution)方法[6]、Radon-WDL变换(RWLT)法[7]、短时傅里叶变换(short time Fourier transform,STFT)和选带快速傅里叶变换(ZooM-fractional Fourier transform, ZooM-FRFT)联合的参数估计方法[8]、蚁群算法[9],不利于硬件实现与实时处理。Shimon等[10-11]所提出的离散多项式变换算法(discrete polynomial transformation algorithm,DPT)可以用很小的计算量对chirp信号进行参数估计,但其对信噪比要求较高在5 dB以上才趋近克拉美罗界,且需要调频斜率是整数时才能获得较好的估计性能。

本文针对传统离散多项式变换算法在低信噪比下无法进行估计和调频率非整数时估计性能不佳的缺陷,在系统中引入基于随机共振(stochastic resonance,SR)信号增强技术,对低信噪比信号进行随机共振处理,提高信噪比。提出了基于CZT的离散多项式变换法(discrete polynomial transformation method based on CZT algorithm,CDPT)和基于RIFE算法的离散多项式变换法(discrete polynomial transformation method based on RIFE algorithm,RDPT)2种新型离散多项式变换算法,对处理后差频信号进行参数估计。同时,对参数估计进行了误差分析。

1 基于LFMCW的测距测速系统

假设图1中A、B、C为参加编队的飞机,它们之间是时钟同步[12]的,在t1时刻由A发出信号,由B、C接收。t2时刻由B发射信号,A、C接收。以此类推。

图1 编队合作测距原理Fig.1 Formation cooperative ranging principle

编队合作测距流程,如图2所示,在飞机编队飞行中,时钟同步情况下,战机A发射端向战机B发射线性调频信号(linear frequency modulated,LFM)信号,与此同时战机B接收端产生LFM信号与接收到的信号进行混频得到差拍信号,然后对差拍信号进行信号处理,估计出速度、加速度、距离等信息。

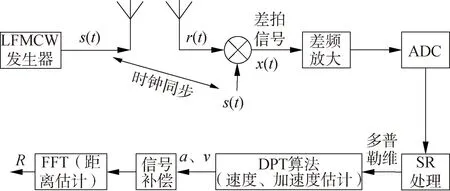
图2 编队合作测距流程Fig.2 Flow chart of formation cooperative ranging

1.1 测距方案

LFMCW测距是通过调制连续波的频率来获得目标信息的,锯齿LFMCW信号的频率曲线如图3所示,其中实线表示发射端发射波型的瞬时频率,虚线表示接收端接收到的波形的瞬时频率。

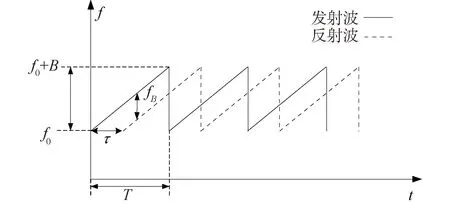
图3 锯齿波LFMCW信号Fig.3 Sawtooth LFMCW signal

发送信号可表示为:

(1)

式中:f0为中心频率;B为调频带宽;T为调频周期;μ=B/T为调频斜率。

接收信号为:

τ≤t≤t≤T+τ

(2)

s(t)与r(t)进行混频,滤除其高频分量,得到差拍信号x(t)[13]为:

(3)

设R0为运动点目标的初始距离、v0为初始速度、a为加速度、c为光速。则目标瞬时距离和回波延时分别为R(t)=R0+v0t+0.5at2和τ(t)=R(t)/c,目标回波在接收机中与发射信号进行正交双通道基带混频,得到M个周期的差拍信号为:

t∈[0,T],m=1,2,…,M

(4)

根据Wojtkiewicz[14]的研究,φ(t,m)可以近似为:

φ(t,m)=φ0+fRt+fvm+fam2

(5)

式中:φ0为与v和a无关的常数;fR=μR0/c;fv=fdT;fd=v/λ为目标多普勒频率;fa=aT2/2λ。

通过快速傅里叶变换(fast Fourier transform,FFT处理各周期差拍信号N点离散频谱可表示为:

SR(n,m)≈S(m)·Sa(n-nR)+N(n,m)

(6)

式中S(m)=ATexp[j2π(fvm+fam2+φ0)]。

由于S(m)的目标回波M点离散多普勒频谱,其幅度|U(k)|为:

(7)

式中D=1+2(MT)2a/λ,k0=fv+D/2。式(7)表明,由于受目标加速度的影响,当D≫1时,多普勒频谱在有效频带D内近似为矩形,其峰值功率下降D倍,从而使目标检测性能显著降低。为消除加速度的影响,首先用多项相位变换方法对目标的加速度进行估计;然后构造补偿函数抵消掉式(6)中S(m)中的二次项fam2,将S(m)变成关于m的一次项,实现加速度的补偿;最后对补偿后的多普勒信号进行FFT处理,估计其速度,再对距离维进行FFT处理估计出其距离,从而实现加速运动目标的距离、速度和加速度的估计。

1.2 基于离散多项式变换的速度和加速度估计

假设离散复信号为:

(8)

则离散多项式相位变换(discrete polynomial transformation method,DPT)定义为:

(9)

式中:L为运算阶数;τ为固定延时;*为共轭运算。

通过DPT处理可以得到式(9)信号的相位系数。具体步骤如下:

1)计算最高项系数cL。

执行L阶DPT操作,并得到:

pL[s(n),τ]=exp{j(ωLn+φL)}

(10)

通过对式(10)进行FFT运算,由频谱峰值对应的值估计出:

cL=ωL/L!τL-1

(11)

2)计算各项系数cl。

(12)

通过式(12)进行FFT运算,由频谱峰值对应的值估计出:

cl=ωl/L!τl-1

(13)

1.3 阵列双稳随机共振

由于离散多项式变换算法存在在低信噪比时无法对信号进行估计的缺陷,参数估计前,先对信号进行随机共振处理,随机共振[15]是由噪声诱导的弱信号放大产生,它将部分噪声能量转化为信号能量,从而来增强信噪比的一种现象。阵列双稳随机共振原理框图如图4所示。

图4 阵列双稳SR模型Fig.4 Model of array bistable SR

阵列双稳随机共振(stochastic resonance,SR)模型系统可由Langevin方程[16]表示:

i=1,2…,N

(14)

(15)

式中:a、b为大于0的实数,是系统势阱的形状参数;n(t)为均值为0,方差为1的高斯白噪声;y(t)为经随机共振处理后的信噪比增强信号。

2 改进的速度和加速度估计算法

由于加速度的存在,混频后的差拍信号的多普勒维被加速度调制成了chirp信号,对加速度和速度的估计问题就转换成了对chirp信号参数估计问题,估计出chirp信号的调频率和载频便可得到加速度和速度。常见的chirp信号估计方法都需要进行二维搜索,所需计算量很大,不利于信号的实时处理。虽然可以实现对chirp信号参数的精确估计,但往往复杂度很高,不易于硬件实现。相对来讲DPT算法所需计算量小,结构简单,易于实现,但对信噪比要求较高且需要调频斜率是整数时才能获得较好的估计性能。针对以上问题,本文在系统中引入随机共振[17-19]来提高信噪比。由于传统DPT算法中使用的FFT算法的栅栏效应的存在,使其不能对信号参数进行有效的估计。本文将传统DPT算法中的FFT基于Rife算法[20]和CZT算法[21]进行改造,得到2种新型离散多项式算法分别命名为基于CZT的离散多项式变换法和基于CZT的离散多项式变换法。

2.1 基于CZT的离散多项式变换法

利用基于Chirp-Z变换的离散多项式变换法(discrete polynomial transformation method based on CZT algorithm,CDPT)算法对速度、加速度频率进行估计:

S(m)=ATexp[j2π(fvm+fam2+φ0)]+n(m)

(16)

对式(14)进行延迟相关处理,得到关于m的函数T(m)为:

T(m)=S(m+L)·S*(m)=

(17)

假设T(m)经FFT的频谱为:

(18)

求出最大谱线X(k0)及其对应位置k0为:

[X(k0),k0]=max{X(k)}

(19)

CZT的起始估计频率与结束估计频率为:

fstart(i+1)=fest(i)-2δ(i)

(20)

fend(i+1)=fest(i)+2δ(i)

(21)

δ(i)=(fend(i)-fstar(i))/M

(22)

式中:fest(1)=k0;fstart(1)=0;fend(1)=fs;i为CZT迭代次数;M为2倍的信号长度。

进行CZT变换:

Z(k)=A·W-m

(23)

其中,

(24)

(25)

[Z(k0),k0]=max{Z(k)}

(26)

(27)

对S(m)进行补偿得到Z(m):

Z(m)=S(m)·B(m)=

ATexp[j2π(fvm+φ0)]+n(m)

(28)

则Z(m)信号FFT频谱Y(k)为:

(29)

求出最大谱线Y(k1)及其对应位置k1为:

[Y(k1),k1]=max{Y(k)}

(30)

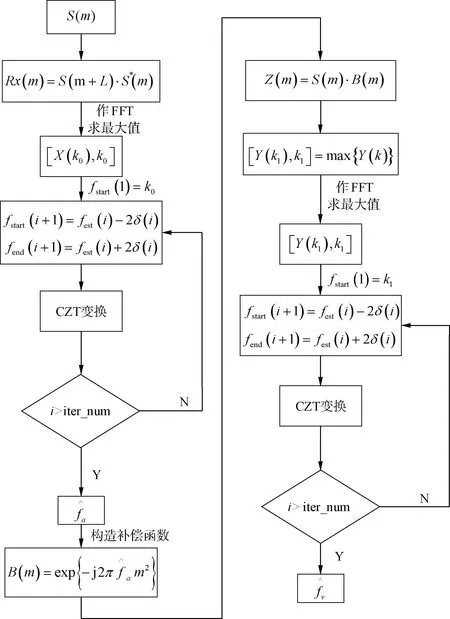
图5 CDPT算法流程Fig.5 CDPT algorithm flow chart

图6 RDPT算法流程Fig.6 RDPT algorithm flow chart

2.2 基于RIFE算法的离散多项式变换法

利用基于RIFE算法的离散多项式变换法(discrete polynomial transformation method based on RIFE algorithm,RDPT)算法对S(m)进行参数估计,具体步骤为:

S(m)=ATexp[j2π(fvm+fam2+φ0)]+n(m)

(31)

对式(29)进行延迟相关处理,得到关于m的函数T(m)为:

T(m)=S(m+L)·S*(m)=

(32)

假设T(m)经FFT的频谱为:

(33)

求出最大谱线X(k0)及其对应位置k0为:

[X(k0),k0]=max{X(k)}

(34)

(35)

(36)

假设频移后的信号FFT频谱为T1(m):

(37)

再根据Rife算法求出估计值:

(38)

(39)

(40)

对S(m)进行补偿得到Z(m):

Z(m)=S(m)·B(m)=

ATexp[j2π(fvm+φ0)]+n(m)

(41)

则Z(m)信号FFT频谱Y(k)为:

(42)

求出最大谱线Y(k1)及其对应位置k1为:

[Y(k1),k1]=max{Y(k)}

(43)

(44)

(45)

假设频移后的信号FFT频谱为Z1(m):

(46)

(47)

(48)

3 算法效果与复杂度仿真分析

本节对信号随机共振增强信噪比和2种新型离散多项式变换算法,也即基于CZT的离散多项式变换法和基于RIFE算法的离散多项式变换法的参数估计误差以及计算量进行了对比分析。在仿真中采用均方根误差(root mean square error, RMSE)作为算法估计性能的度量标准。设置采样频率为200 GHz,时间为10 μs,采样点数为2×106个。

3.1 随机共振仿真分析

本节通过仿真对正弦信号和线性调频信号经随机共振处理后的提升效果进行了分析。

由图7、8仿真结果可以看出,经随机共振处理后的正弦信号和LFM信号信噪比得到了明显的提升。

图7 经随机共振处理的正弦信号Fig.7 Sinusoidal signal processed by stochastic resonance

图8 经随机共振处理的LFM信号Fig.8 LFM signal processed by stochastic resonance

3.2 算法估计误差分析

下面对CDPT算法和RDPT算法估计误差与DPT算法和克拉美罗界进行了对比分析,进行了500次蒙特卡洛仿真得到下面估计误差曲线。

经蒙特卡洛仿真进行误差分析,由图9和图10可以看出传统DPT算法没接近克拉美罗界,不能进行有效的估计,RDPT算法和3次迭代CDPT算法估计误差曲线几乎重合。仿真结果表明在信噪比-20 dB时均方误差开始接近克拉美罗界。

图9 不同SNR下频率(速度)估计值的RMSEFig.9 RMSE of frequency (velocity) estimates at different SNRs

图10 不同SNR下调频斜率(加速度)估计值的RMSEFig.10 RMSE of FM slope (acceleration) estimation under different SNRs

RDPT和3次迭代CDPT算法在较低信噪比下可实现有效的估计,也即可以实现低信噪比下加速度、速度的有效估计。

3.3 算法计算量分析

本节对算法计算复杂度进行了分析,如表1所示。

表1 计算量分析Table 1 Calculation analysis

经上述分析,由图11可以很直观的看出RDPT算法计算量和DPT算法计算量接近,两者计算量远小于3次迭代CDPT算法的计算量,便于实时估计。

图11 计算量分析柱状图Fig.11 Calculation quantity analysis histogram

4 结论

1)本文针对传统DPT算法对信噪比要求较高且调频率非整数时估计性能不佳等缺陷,对LFM信号进行随机共振处理,经随机共振处理后的LFM信号信噪比得到了明显的提升。

2)针对加速度估计精度不高问题,提出2种新型离散多项式变换算法,CDPT算法和RDPT算法,经蒙特卡洛仿真进行误差分析,仿真结果表明传统DPT算法估计性能不佳,RDPT算法和CDPT算法在信噪比-20 dB时均方误差开始接近克拉美罗界。RDPT算法与3次迭代CDPT算法均可在较低信噪比下可实现调频斜率的有效估计,且性能接近,即二者均可实现低信噪比下速度、加速度的有效估计。

3)对2种算法计算量进行了分析,经分析RDPT算法与DPT算法计算量接近,远小于3次迭代CDPT算法计算量。