高地应力条件下隧道多力学特性锚杆模型及应用研究

张春瑜

(中铁十八局集团有限公司, 天津 300222)

0 引言

复杂地质条件下围岩支护系统的稳定性分析一直是我国隧道工程建设的焦点和难点。锚杆支护是控制围岩变形的重要手段,也是新奥法地下硐室工程的主要支护方式之一;而在高地应力、大埋深、围岩软弱破碎和动载扰动等复杂工况下,锚杆常常出现断裂破坏现象[1]。由于地质条件复杂,大量工程在进行支护设计时难以判断合理的支护强度。为避免结构失稳,支护设计往往过于保守,从而造成了经济上的浪费。因此,合理的支护失效判别方法对围岩稳定性分析及工程经济性建设具有重要意义。

数值模拟是工程稳定性分析的常用方法。在本构模型优化方面,陈育民等[2]通过FISH平台对FLAC3D中的邓肯-张模型进行改进,并通过一系列三轴试验算例对模型进行验证;蓝航等[3]建立考虑初始损伤的节理岩体弹塑性本构模型,并通过VC++开发平台将模型嵌入FLAC3D软件中进行露天矿边坡模拟计算;王春波等[4]基于塑性增量理论,利用VC++开发环境编写硬化土本构关系计算程序,同时将室内试验与模拟试验进行对比,验证了本构关系的正确性;陶惠等[5]将堆石料三维边界面模型和非线性强度准则相结合,利用FLAC3D实现三维边界面本构模型的二次开发,并开展三轴试验进行模型验证;杨云浩等[6]基于弹塑性损伤力学和非关联塑性流动法则,利用FLAC3D二次开发平台构建了适用于高硬度岩体的各向异性损伤模型;左双英等[7]利用VC++开发环境将基于Zienkiewicz-Pande屈服准则的弹塑性本构模型嵌入FLAC3D中,进一步提高了FLAC3D的计算速度。

本构模型的优化使模型计算过程中的围岩体力学响应更加合理,还有部分学者对支护结构模型进行了优化。例如: Li等[8]基于FLAC3D对钢拱架Beam和锚杆Cable单元进行二次开发,给定支护结构失效判据;Guo等[9]对空间变化条件下开挖的圆形隧道支护衬砌进行二次改进,并开展了可靠性分析;戚德印等[10]通过二次开发减少了结构单元节点数对计算结果的影响;王建华等[11]通过二次开发实现了空间m法在有限元软件中的应用,并通过现场实测数据进行了验证;杨珺博[12]利用ANSYS软件中的APDL语言对支护单元进行二次开发,实现了支护单元对围岩反向加载的功能;祝少纯等[13]利用改进的伯努利双纽线原理建立“蝴蝶筋”数学模型,实现了钢格栅钢架的快速建模与布置;刘兆新等[14]利用Revit进行二次开发,改进了隧道支护模型构建算法,提高了支护模型构建速度;秦幼林等[15]对岩石本构模型进行了分类整理,并对膨胀岩本构模型进行了总结。

综上所述,国内外学者在采用数值计算方法对锚杆模型的改进上取得了重大突破,但计算模型本构关系的优化无法判断支护结构是否失稳,二次开发的支护结构单元也不能直观地显示模型的破坏形式,存在一定的缺陷。本文基于FLAC3D有限差分软件内置的FISH二次开发平台,改进Cable单元及其建模方法,构建多力学特性锚杆模型(multi-mechanical, MMC模型),并开展锚杆拉拔试验对MMC模型进行验证,以期为复杂隧道工程支护设计及其稳定性分析提供参考。

1 FLAC3D内置锚杆模型及缺陷

1.1 Cable模型的基本应用

Cable模型是FLAC3D中的内置支护模型,常用来模拟锚杆或锚索结构,其本质是由多个组合在一起的圆柱体单元组成。Cable单元特征如图1所示。每个Cable单元由2个节点和1段杆件单元组成,并且每个单元都有自己的局部坐标系统。图1中: 将x定义为Cable单元的轴向,由a点指向b点,x,y则定义了杆体的截面方向;由于Cable单元只存在轴向刚度,因此,Cable单元在运行时只产生轴向位移u1和u2,同时根据杆体本构关系产生轴向力。

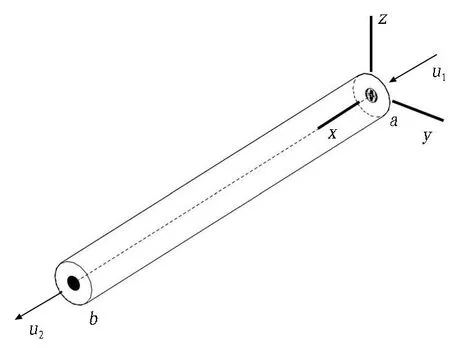
图1 Cable单元特征[16]

Cable单元在模拟锚杆或锚索时,不仅能够体现锚杆的杆体特点,而且还能模拟注浆体的变形特征。在构建锚固支护模型时,杆体的节点Node会与围岩的结点Gridpoint之间构建Link单元,模型会将浆体参数自动赋予到锚固段的Link单元上。浆体参数包括黏聚力、内摩擦角、剪切刚度、注浆体周长等。围岩、杆体和注浆体共同组成锚固支护计算响应系统。

1.2 Cable模型力学行为

1.2.1 轴向力学行为

由于锚杆或锚索材质通常为钢材,因此Cable单元在轴向上表现出理想的弹塑性力学行为,如图2所示。图2中:Ft和Fc分别为锚杆(索)抗拉强度和抗压强度;F为轴向应力;U为轴向变形。如果在赋予参数过程中并未赋予锚杆模型Ft和Fc,则杆体将被设为弹性体,不发生屈服。弹塑性Cable单元轴向本构关系如式(1)所示[17]。

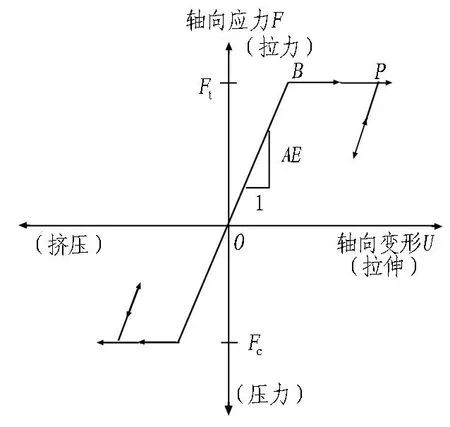
A为杆体截面面积; E为锚杆弹性模量; B点为弹塑性分界点; P点为塑性变形中的任意一点。

(1)

式中:K为杆体轴向刚度; ΔU为轴向变形差值。

在弹性阶段(图2中OB段),锚杆轴力与变形为线性关系,斜率为锚杆模型轴向刚度,计算公式为:

(2)

式中l为锚杆长度。

在锚杆轴力达到Ft后,杆体进入塑性阶段(图2中BP段),具体表现为杆体刚度降为0 N/m,轴力保持不变,轴向变形无限增大。

1.2.2 锚固剂轴向力学行为

由于锚固砂浆的存在,Cable单元所模拟的锚固剂在轴向同样表现为弹塑性力学行为。FLAC3D软件中用弹簧-滑块模型来表示本构关系。浆体材料力学行为曲线如图3所示。

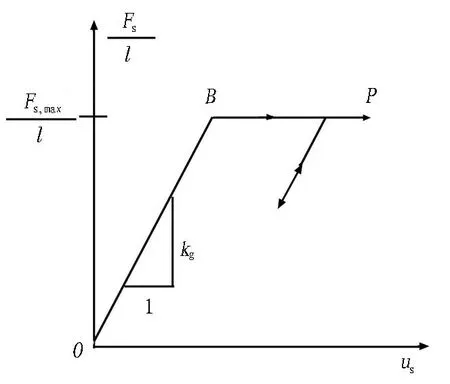
Fs为浆体轴向受力; Fs,max为最大轴向力; kg为浆体轴向刚度; us为浆体沿锚杆的轴向变形。

由图3可知,浆体沿轴向力学行为同样分为弹性阶段和塑性阶段。当浆体处于弹性阶段(图3中OB段)时,浆体本构关系如式(3)所示。

(3)

当浆体处于塑性阶段(图3中BP段)时,浆体轴向应力Fs,max保持不变,切向变形无限增大。其中,Fs,max的计算公式如式(4)所示。

(4)

式中:cg为浆体黏聚力;φg为浆体内摩擦角;pg为浆体界面周长;σm为围岩之间的应力,在软件迭代计算过程中通过内置算法自动生成。

1.3 Cable模型应用评价

通过上述分析可以发现,利用Cable单元模拟的锚杆具有以下特点:

1)Cable单元能够模拟锚杆轴向拉伸行为,且在弹性阶段表现良好,但当锚杆进入塑性阶段后,Cable单元开始无限变形且对围岩提供持续拉力,这与锚杆实际受力状态不符。

2)Cable单元可以模拟砂浆轴向变形特征,能够满足精度要求不高和工况简单的常规模拟,但在复杂工况下所表现出来的塑性力学行为与实际存在较大偏差。

2 多力学特性锚杆模型二次开发

2.1 MMC模型开发原理

在实际工程中,锚杆或锚索的破坏形式可分为杆体断裂和锚固段脱落。为使数值模拟结果更符合实际力学特性,从锚杆及锚固剂轴向本构关系出发对Cable模型进行改进。在轴向上,锚杆在锚固过程中会产生拉伸变形,当变形超过自身极限延伸率时,锚杆会发生断裂破坏,此时整个杆体轴力降为0 kN,因此,对锚杆轴向本构模型进行修正。锚杆轴向修正力学模型如图4所示,其表达式如式(5)所示。

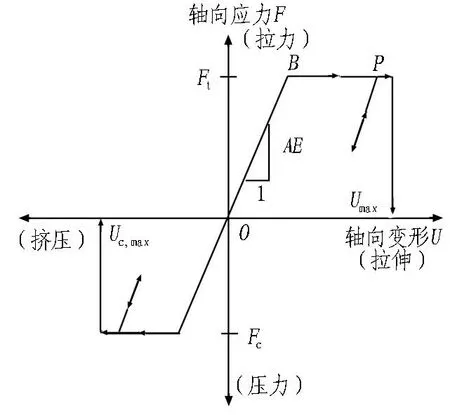
Umax为最大轴向变形; Uc,max为最大挤压变形。

(5)

与原模型相比,此时的锚杆模型能够依据断裂判据模拟锚杆断裂失效时的力学行为,但不能模拟锚杆的破坏形态。为进一步体现锚杆断裂形态,将锚杆单元进行离散化处理,即将每个Cable单元体都视为独立的个体,众多单元体通过Link模型逐个连接,最终形成锚杆模型。当离散处理后的锚杆某个节点受力达到破坏准则时,则自动删除与该节点相连接的Link单元,以模拟锚杆的断裂效果。

在轴向上,锚杆通过浆体与围岩相连接,在锚杆不断发生拉伸变形的同时,浆体也受到剪切力的作用。由于浆体塑性变形较小,因此,计算时可以不考虑塑性变形,即当剪切力超过浆体抗剪强度时浆体发生开裂破坏。锚固剂轴向修正力学模型如图5所示,本构关系表达式如式(6)所示。

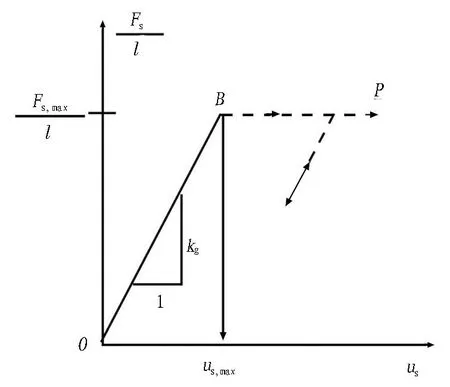
us,max为浆体沿锚杆的最大变形。

(6)

此时模型只是和实际锚固浆体力学行为相似,但并不能模拟浆体破坏形态。浆体单元本质为锚杆单元与围岩相连接的Link,因此,在浆体模型某个Node节点达到破坏准则时将Link删除即可模拟浆体破裂。

需要说明的是,FLAC3D内置有FISH语言编译环境,上述本构模型算法可通过FISH语言嵌入到FLAC3D计算主程序中[16]。

2.2 MMC模型开发流程

为了使Cable单元能够更加真实地模拟锚杆的失效断裂特征,从而提高锚杆支护结构稳定性分析的精度,本文基于FLAC3D中的FISH语言对原有Cable模型进行改进,构建MMC模型。MMC模型开发流程如图6所示。

图6 MMC模型开发流程[18]

1)通过FLAC3D构建隧道开挖模型,根据工程设计,在围岩上选取锚杆起点位置,即实际工程中的钻孔位置,并确定锚杆方向。在1#起点位置到L1位置点处构建一段Cable单元,并将该锚杆单元定义为“ID1”,如图7(a)所示,直到所构建的单元达到预设数量。

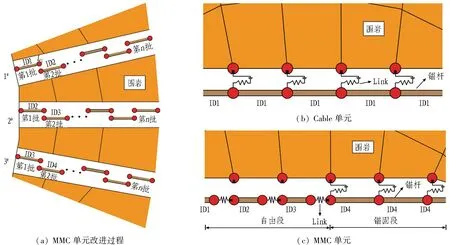
图7 多力学特性锚杆单元原理图

2)此时,所构建的Cable单元均通过Link与Zone相连接,保留部分Link,将其余Link删除,通过“structure link create target node range structure-type cable”命令在Cable单元节点之间构建Link,如图7(b)所示。

3)将Link进行分组,将保留的Link定义为“锚固段”,将重构的Link定义为“自由段”,分别对2组Link进行赋值,如图7(c)所示。

4)计算中通过不断获取Link的应力(应变)数据,对Link的受力状态进行循环判断。当Link的受力超过极限应力或应变值时,通过FISH语言将Link删除,以模拟锚杆的屈服破断过程。

2.3 MMC模型试验验证

为检验所构建的MMC单元的合理性,在室内开展全长黏结锚杆拉拔试验,并基于FLAC3D利用MMC模型进行模拟试验,与室内试验结果进行对比分析。拉拔试验采用直径为14 mm的钢筋作为锚杆,花岗岩作为构件基体,水泥砂浆作为浆体材料。拉拔试验材料力学参数如表1所示。试验过程中设置2种锚固长度,分别为400 mm和200 mm,以获得不同的锚固力。

表1 拉拔试验材料力学参数

根据表1中各材料力学参数,利用MMC单元构建试验模型,开展锚杆拉拔模拟试验。拉拔试验加载过程如图8所示。可以看出,由于锚固力的不同,锚杆出现2种失效形式: 当锚固力大于锚杆屈服强度时,锚杆发生断裂失效,体现了锚杆轴向力学行为;当锚固力小于锚杆屈服强度时,锚杆发生脱锚失效,体现了锚杆与围岩的切向力学行为。

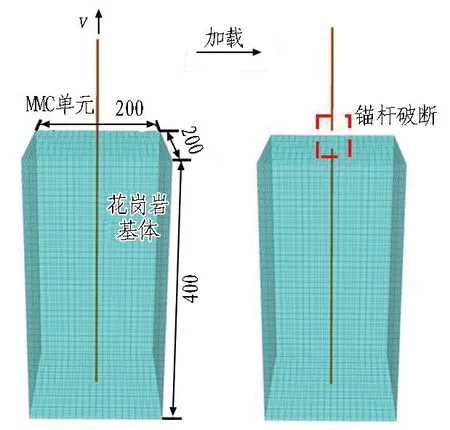
(a) 锚杆断裂失效(单位: mm)

拉拔试验曲线对比如图9所示。可以看出: 当锚固力大于锚杆屈服强度时,锚杆轴力随着变形逐渐增加,荷载-位移曲线初始阶段呈线性关系。当荷载达到63.1 kN,位移达到8.2 mm后,荷载转变为平缓上升趋势;直至荷载达到69.8 kN,位移达到50.6 mm时,曲线荷载降为0 kN,锚杆发生断裂,与试验测得锚杆破坏荷载70.6 kN较接近,误差为1.1%。当锚固力小于锚杆屈服强度时,荷载仍为线性增加。当荷载达到40.1 kN时,浆体与锚杆脱离,轴力降为0 kN,与试验得到的脱锚荷载41.3 kN较接近,误差为2.9%。试验结果表明,MMC模型基本能够展现出锚杆的真实受力变形及破坏特征,满足模拟锚杆失效的要求。

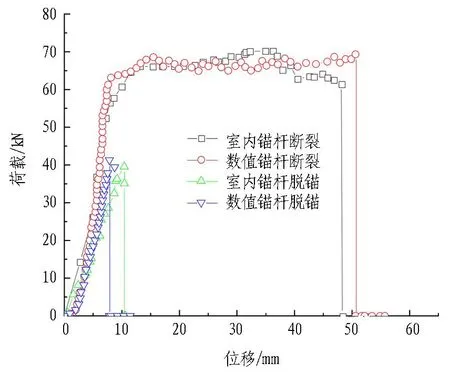
图9 拉拔试验曲线对比

3 MMC模型工程应用分析

为进一步研究MMC模型在实际工程模拟中的优势和适用性,以月直山隧道为例,开展MMC和Cable锚杆模型对比分析,并将数值计算结果与工程监测曲线进行对比。

3.1 工程概况

月直山隧道全长14 085 m,中心里程为D2K383+891,隧址区属大渡河高山剥蚀地貌,地形起伏较大,大渡河、牛日河深切,地面高程880～2 700 m,隧道最大埋深约1 820 m,属高地应力隧道。隧址区基岩大部分裸露,区域性断裂构造发育,节理间距为1～2 m,呈密闭—微张状,延伸性较好,部分节理面有粉质黏土或粉土充填。通过室内试验测得围岩弹性模量Ec为16.6 GPa,泊松比μ为0.25,峰值黏聚力cp为1.1 MPa,峰值内摩擦角φp为31°,残余黏聚力cr为0. 6 MPa,残余内摩擦角φr为26°。

现场采用锚杆、喷射混凝土和钢拱架联合支护方式,支护参数如表2所示,其中锚杆施加40 kN预应力。现场支护系统构建完成后,随着工作面推进,二次衬砌出现变形破坏,如图10所示。通过现场观测,发现开裂原因为锚固浆体参数设计较小,导致部分锚杆脱锚,致使支护系统支护能力降低,围岩侵入二次衬砌。

表2 混凝土及锚杆参数

图10 二次衬砌变形破坏

3.2 支护稳定性计算

根据现场围岩及支护参数,构建月直山隧道二维支护模型,其中,混凝土采用Liner模型模拟,钢拱架采用Beam模型模拟,锚杆分别采用Cable和MMC模型模拟。二维三心圆隧道支护模型如图11所示。模型尺寸为100 m×100 m×0.2 m(长×宽×厚),顶拱半径为5 m,侧拱半径为1.13 m,仰拱半径为13.6 m。计算完成后,提取计算云图,如图12所示。

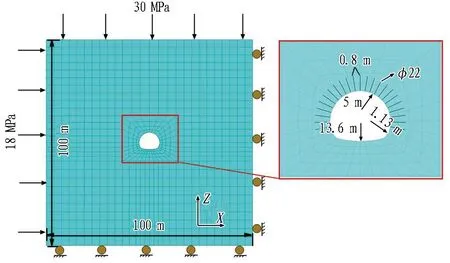
图11 二维三心圆隧道支护模型

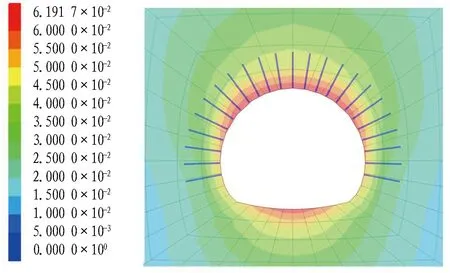
(a) Cable模型支护

由图12可以看出,利用Cable模型模拟锚杆支护时,围岩最大变形量为6.19 cm,利用MMC模型模拟锚杆支护时,围岩最大变形量为17.32 cm,二者均显示围岩最大变形发生在拱顶。结合现场情况可以发现,二次衬砌预留变形量为15 cm,Cable模型计算结果表明围岩变形未超出预留变形量,而MMC模型计算结果显示围岩变形量已侵入二次衬砌,并且锚杆破坏形式符合现场结论。

3.3 现场监测对比分析

现场利用锚杆测力计对部分锚杆变形及受力进行监测,监测位置包括拱顶、拱腰及拱脚。锚杆监测装置安装如图13所示。本文以拱顶锚杆为例,将现场锚杆监测曲线和数值计算结果进行对比,进一步验证MMC模型的工程适用性。监测曲线对比如图14所示。

图13 锚杆监测装置安装

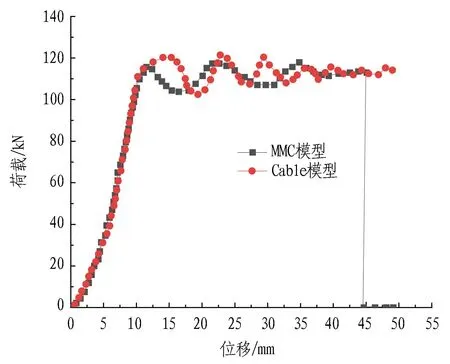
(a) 数值计算曲线

由图14(a)可知,MMC锚杆模型能够产生弹性变形与塑性变形,并且在轴向达到45 mm时锚杆支护失效,轴力降为0 kN。结合图12(b)可以看出,锚固段发生破坏,而锚杆自由段完整,表明锚杆失效是由于锚杆轴力超过锚固剂抗剪强度而发生脱锚破坏,并未发生拉伸断裂。图14(a)中显示Cable单元只存在弹性及塑性变形,而通过图12(a)可以看出Cable单元并不能展现锚杆失效特征,因此,Cable单元对围岩持续产生支护作用,使得计算结果小于真实围岩变形。

由图14(b)可知: 现场监测数据显示锚杆前23 d内轴力持续增加,围岩变形量缓慢增长,最终锚杆轴力稳定在120 kN;在监测时间达到64 d时锚杆轴力降为0 kN,说明锚杆失效,此时围岩变形速度加快,最终稳定在180 mm。对比监测数据与数值模拟结果可知,MMC模型能够模拟现场锚固系统失效,失效后的MMC模型不再为围岩提供支护力,计算得到的围岩变形量17.32 cm更接近现场实测值18 cm。因此,相比于Cable模型,MMC模型更适合用于围岩稳定性分析。

4 结论与讨论

本文通过有限差分软件FLAC3D内置的FISH二次开发平台,对传统Cable模型进行修正,建立了MMC模型,并通过锚杆拉拔试验及工程验算对模型应用效果进行分析,得到以下结论。

1)FLAC3D内置的Cable模型所模拟的锚杆具有理想弹塑性本构关系,但无法模拟锚杆失效,提出的锚杆轴向U>Umax及锚固剂轴向Fs>Fs,max失效判据修正了Cable模型轴向及切向本构方程,为模拟锚杆失效提供了可能。

2)通过FISH语言将Link模型与失效判据相结合所构建的多力学特性锚杆模型(MMC模型)能够实现锚杆及锚固剂轴向失效。通过开展锚杆拉拔试验发现,利用MMC模型构建的模拟试验计算结果与室内试验结果较为接近,最大误差为2.9%,验证了MMC模型的适用性。

3)通过工程应用算例分析发现,采用MMC模型进行模拟能够直观地看出锚杆断裂位置,破断后的MMC模型不再为围岩提供支护,得到的计算结果基本符合现场监测数据,相对于Cable模型,MMC模型更符合现场锚杆实际力学特性。

锚杆在实际工作中的受力通常较为复杂,除拉伸作用外,锚杆在穿过岩层节理面或软弱夹层时还易受到剪切作用,由于锚杆剪切破断而导致的工程事故时有发生。因此,在后续工作中,应考虑锚杆受到的剪切作用,针对锚杆穿越复杂破碎带时的力学特性开展研究。