面向切削力修正的机床主轴回转精度预测实验分析

孙备，张玲玲，李峰，赵凯绅，王翠芳

(1.焦作大学 机电工程学院，河南焦作 454000；2.河南理工大学机械与动力工程学院，河南焦作 454000；3.瑞庆汽车发动机技术有限公司，河南焦作 454000)

0 前言

机床主轴位置参数控制精度已经成为工件加工外形尺寸与表面性能的关键因素，也是评价主轴综合控制效果的一项重要指标[1]。现阶段，关于主轴回转精度的研究工作基本上是从回转精度影响机制、主轴回转和工件精度关系、回转参数测试方法、主轴回转精度调节层面考虑的[2-3]。而当主轴保持高速切削状态时，不同的切削载荷与转速也会造成主轴回转精度的改变，以空转状态测定的主轴回转精度无法准确体现主轴实际加工精度[4-5]。当前主轴回转精度测试需要设置复杂的步骤，而且要求测试装置具备很高的精度，无法实现主轴切削期间回转精度的实时测试。构建机床主轴运动学模型，再以该模型实时预测回转精度，由此实现主轴切削阶段回转精度的准确评估[6]。

目前，已有许多学者开展了主轴动力学的研究工作，构建了动力分析模型并实现了振动响应、模态处理与数据优化分析[7]。其中，KARACAY和AKTURK[8]选择角接触球轴承刚性转子磨床主轴作为测试对象，探讨了主轴沿不同方向摆动时产生的振动信号；KIM和 LEE[9]针对主轴构建了动力仿真模型，考虑了轴承配合间隙的影响，深入分析了结构参数、运行工况与热因素引起的主轴系统动力性能的变化。国内研究人员陈小安等[10]设计了一种立式主轴模型，评价了轴向振动信号、热性能及其对主轴精度产生的影响。CAO等[11]同时利用Gupta轴承动力模型与转子有限元模型设计主轴运动过程的分析模型，再以上述模型测试了各种工况条件下的主轴系统动力响应性能。现阶段，多数学者都是通过构建主轴动力模型的方法进行主轴刚度与固有频率的分析，在此基础上进行参数优化。虽然已有许多学者开展了滚动轴承动力学模型的简化工作，但很少有关于主轴回转精度方面的预测报道。

本文作者根据XI等[12]提出的高速主轴仿真模型，设计一种可以精确预测不同切削工况条件的主轴回转精度分析方法。首先为高速主轴系统构建运动控制模型；之后设计以上述模型实现的回转精度预测方法。为验证回转精度预测结果的准确性，建立一套不需要通过标准球实现的主轴回转精度分析系统，可以针对具体切削工况开展主轴回转精度测试。

1 回转精度预测方法

机床主轴的回转误差可分为同步误差和异步误差2种基本类型。由于主轴切削阶段存在大量噪声，导致异步误差分析结果受到较大影响。文中建立的运动仿真模型还无法满足切削噪声的分析要求，因此通过建立主轴运动模型进行同步误差的预测分析。图1所示为此次构建的运动模型预测主轴回转精度的流程[13]。

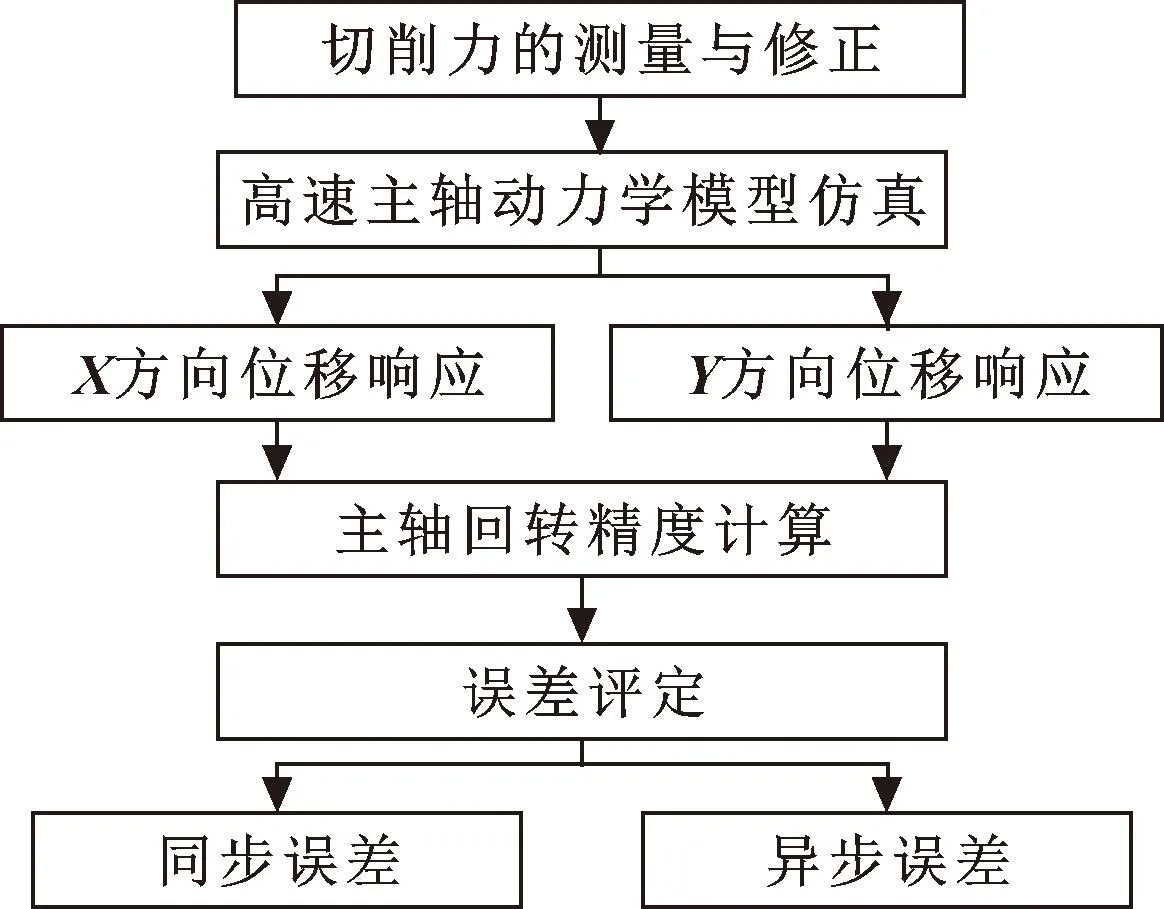
图1 回转精度预测流程

实验中通过在主轴上安装测力仪来测定切削载荷，之后对它进行修正调整。先从测力仪频响函数中提取得到有用信息，之后对各个方向的测力仪固有频率进行样条拟合插值处理，获得X、Y、Z方向上的切削力频率系数。对特定方向测试切削力载荷，之后完成切削力的傅里叶转换，得到的离散频率变化幅值与该方向离散频率切削载荷幅值因子进行乘积运算，由此得到修正后的切削载荷频谱数据。之后再对修正切削力傅里叶转换频谱完成逆傅里叶处理，得到切削力。设定主轴转速为6 000 r/min，切宽尺寸为2 mm，切深为1.6 mm及进给速率为500 mm/min时，切削力修正前后曲线如图2所示。可知：只有经过修正才能从切削载荷中获取有效的信息。

图2 切削力修正前后对比

2 试验验证

2.1 试验设置

图3所示为利用三点法测试主轴回转精度所采用的设备结构示意。测定主轴回转精度时，以奇石乐测力仪为测试设备，再将切削载荷数据输入计算机系统，经过运算得到最终结果，设定频率为6 000 Hz，再对切削载荷进行数据采集。将测试面设置在主轴刀柄光滑面处，并在截面处设置了3个雄狮位移测试器。按照分度盘参数完成传感器安装后，保持传感器的安装方向和目标值处于相同状态。此次设定位移传感器灵敏度为80 000 mV/μm，量程为0～250 μm。调节传感器采集获得的位移参数后，再利用数据采集器处理上述数据，之后将处理结果传输到计算机存储中心。根据图4流程确定回转精度[13]，以同步平均算法来降低位移信号噪声。

图3 切削工况下主轴回转精度测量

图4 回转精度计算流程

分别对表1所示3种工况进行切削，得到主轴回转精度以及切削载荷。通过测试发现，各工况下都保持6 000 r/min的转速。处于变进给工况下的速度变化阶梯为200 mm/min，同时设定变切宽阶梯为2 mm，变切深阶梯为0.2 mm。

表1 回转精度测量工况

将上述工况下形成的传感器信号通过图4回转精度计算流程确定各工况下的主轴回转精度，之后确定各工况误差，如图5所示。

图5 不同工况下回转精度计算结果

由图5可知：在变进给以及变切深的过程中，随着进给速率和切削深度的改变，形成了规律性的同步误差，并且切深受到同步误差因素的影响程度最大，而进给速度次之。受噪声因素的影响，异步误差也产生了无规则变化的现象。在变切宽状态下，各切宽参数形成的同步误差相近，这是由于实验测试期间改变切宽后，切削力基本保持恒定。

图6所示为各切深下得到的X方向切削载荷。可知：同步误差与切深关系和切削力幅值变化特点接近，表现为具有随机性的异步误差，以上均为预测同步误差所得的结果。由图7可知：受切削载荷的影响，主轴回转精度也发生了显著改变，此时同步误差和切削载荷具有明显的正相关关系。根据上述结果可以推断在特定切削工况下进行主轴回转精度分析具备较大应用价值。

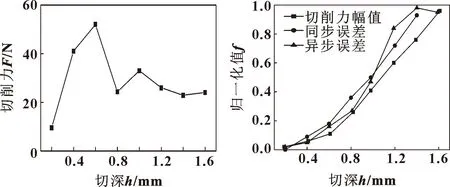
图6 不同切深下的切削力

2.2 结果对比与分析

对各个切削工况下得到的X、Y、Z方向的切削力进行修正，再将修正后参数输入主轴模型的刀尖处。设定切深为0.2 mm，切宽为2 mm，并保持进给速度等于500 mm/min，通过仿真测试得到的振动位移如图8所示。可知：不同切削工况下出现了位移响应大幅波动的现象。

图8 仿真振动位移响应结果

根据回转精度指标以及误差评价模型，测试了此实验工况下仿真后的振动位移响应。图9所示为不同工况下开展仿真测试得到同步误差与实际误差的差值。

图9 切削工况下仿真与试验对比结果

由图9可知：在变进给以及变切宽条件下测试得到的结果与仿真结果相近，最大误差为0.2 μm。在较小的变切深参数下开展仿真处理与实际测试时所得的结果相近，随着切深的持续增加，2种方式所得的结果差异也更明显。这是因为切深增大后会形成更大的振幅，导致测试位移信号中包含了大量噪声。噪声环境中误差分离精度会受到明显影响，已经不能分离获得精确的圆度误差[14]。

主轴进入低速空转运行状态时只存在很弱的噪声，以分离后圆度误差作为实际圆度误差。图10所示为不同变工况下圆度误差结果。可知：设定变切宽与变进给时分离得到的圆度误差规律基本一致；变切深条件下的圆度误差与其相比具有显著差异。同时也可以通过权函数放大误差分离时形成的噪声强度，导致回转精度的下降。

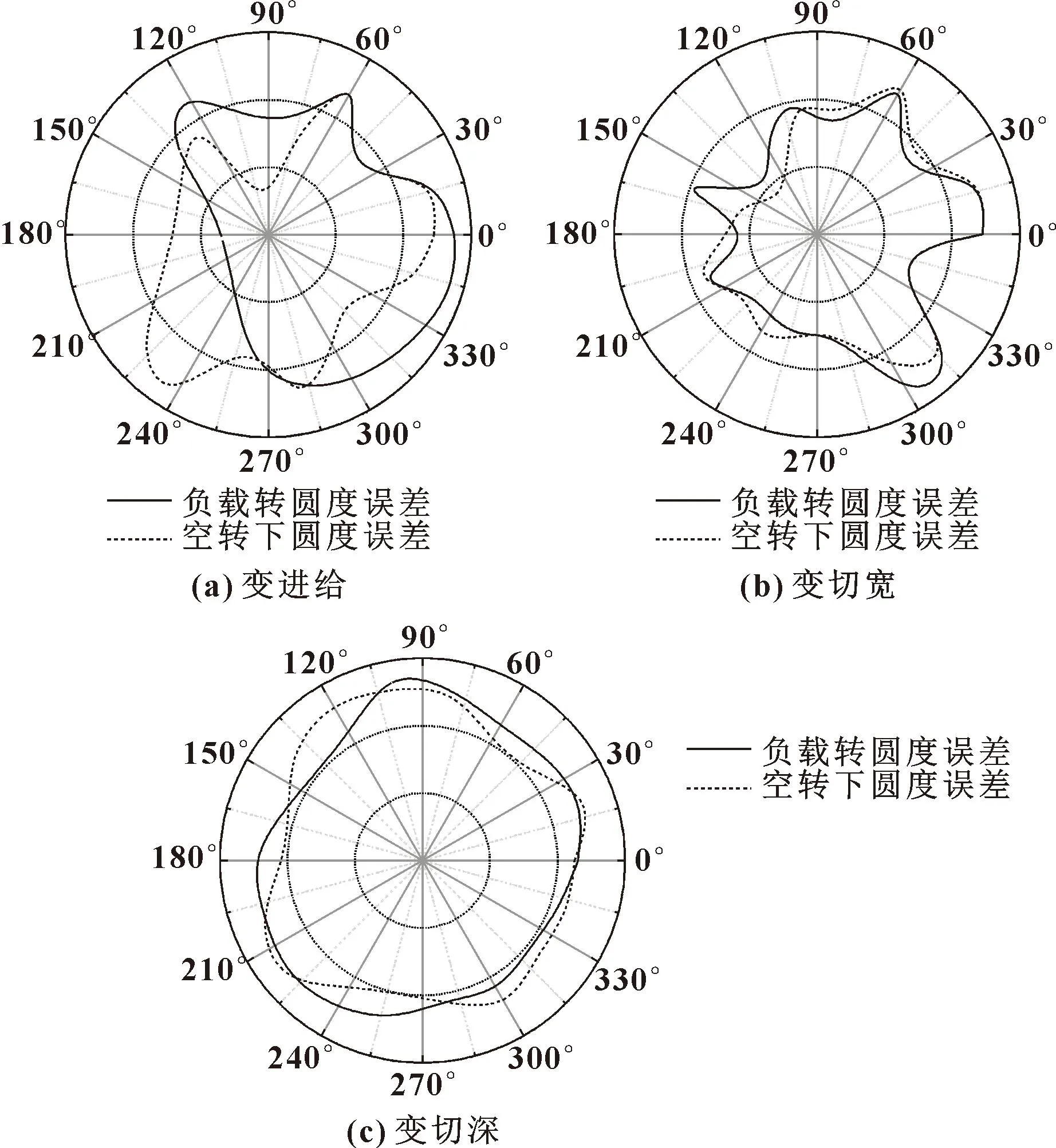
图10 不同变工况下圆度误差结果

3 结论

(1)随着进给速率和切削深度的改变，形成了具有规律性的同步误差，切深受到同步误差因素的影响程度最大，而进给速度次之。受切削载荷的影响，主轴回转精度显著改变，同步误差和切削载荷具有正相关关系。

(2)变进给以及变切宽条件下测试与仿真结果相近，最大误差为0.2 μm。设定切宽12 mm与进给速度1 200 mm/min时分离得到的圆度误差与100 r/min空转时的圆度误差相吻合。