基于多层级指标清洗与聚合的科技创新能力评价研究

刘钰莹，王一峰，李伯泽

（1.清华大学深圳国际研究生院，广东深圳 518055；2.哈尔滨工业大学（深圳），广东深圳 518055）

0 引言

在当前世界百年未有之大变局的背景下，科技自立自强已经成为建设社会主义现代化国家的时代要求。科技创新不仅是国家发展的重要支撑，更是国际竞争力的重要标志。科技创新能力评价作为科技评价领域的重要内容之一，旨在对从事科研活动的主体（一个国家、地区或者一家科研机构等）的科技创新能力进行评估［1］。科技创新能力评价不仅可以定位科研活动主体的创新优势和劣势，激发其创新热情，还可以为科技计划的布局、科技政策措施的制定、科技资金的分配提供参考［2］，推动科技创新发展，提升科技创新水平。

科技创新评估的起源可追溯至美国［3］，而后日本、英国、德国等发达国家发展出具有本国特色的科技评估机制，科技创新评估逐渐成为世界各国科技制度中的重要组成部分。20 世纪五六十年代，科技创新评估处于起步阶段，加菲尔德［4-5］和莫德［6］等人先后运用文献计量学方法进行科技创新评估实践，文献计量学开始广泛应用于科技创新综合评价中。20 世纪七八十年代，科技创新评估进入定量分析阶段，层次分析法开始被应用于科技评估中［7］。20 世纪90 年代后，科技创新评估进入多指标、综合评价阶段，科技评估方法逐渐多样化，出现主成分分析法、模糊综合评价法、灰色关联分析法（GRA）、优劣解距离法、因子分析法等方法。近年来，以大数据、人工智能、文本分析等技术为基础的评估方法也被越来越多地应用于科技创新评估领域，多源异构数据的融合应用成为科研评价和管理的趋势［8］。

中国的科技创新评价起步较晚，发展路径主要沿袭国外先进经验。21 世纪以来，中国科技评价经历了从传统单一的技术评价到综合评价的转变，也开始注重评价方法的规范化。近年来，科技创新能力评价不断深化和拓展，但仍未形成普适的综合评价方法体系框架。从国内相关研究来看，中国科学技术发展战略研究院［9-10］的《中国区域科技创新评价报告》和《中国企业创新能力评价报告》通过设定指标标杆，基于指数法进行多级综合评价；中国科学技术发展战略研究小组等［11］的《中国区域创新能力评价报告》通过专家评分法确定指标权重；Heng［12］采用非线性加权综合评价方法对河南省大中型工业企业进行实证分析；赵勇等［13］应用层次分析法确定国家科学中心的多级评价指标权重；侯静等［14］运用主成分分析法完成对评价指标降维和赋权；周晶晶等［15］使用因子分析法，根据累计贡献率和因子荷载矩阵对中国14 个城市的创新能力进行综合评价；冯伟等［16］针对科技资源评价指标所体现出的“灰色”特征，运用多层次灰色评价法构建了科技资源整合效果评价模型；桑秀丽等［17］将灰色分析理论中灰色关联度结合优劣解距离法（TOPSIS）算法引入高校创新能力综合评价当中；蔡晓琳等［18］结合熵权法应用优劣解距离法，基于评价对象与理想解之间的距离评价珠三角9 个城市的科技创新能力。张霞等［19］和芦苇［20］认为，上述综合评价方法都有各自的特点和适用条件，具有一定的局限性：专家评分法和层次分析法依赖大量前期专家的评分工作，工作量大，且评价结果的公正性和可信度易受人为主观因素的影响；指数法和加权综合评价法的计算较为简单，但指数法的评价指标基准不易确定，评价数据质量会在很大程度上影响评价结果的可靠性；主成分分析法、因子分析法不适用于评价指标较多的多级综合评价问题，在可解释性、直观性、可比性上存在一定局限；相比之下，灰色关联分析法、优劣解距离法等综合评价方法充分利用评价数据中蕴含的信息，评价结果更加精确，但仍存在应用场景的局限。因此，构建一个能够提高数据可信度、实现可迁移性、适应多种算法的多级综合评价算法框架，提升科技评价的效率、准确性和科学性具有十分重要的意义，符合科技评价改革的价值导向。

科技创新能力评估是一项复杂的综合评价任务，涉及复杂的指标体系设计和深度的数据处理［21］。为此，本研究提出了一种基于指标聚合并集成指标清洗算法的综合评价框架，构建可信度高、精确度高、稳健性强的评价模型，并从政府部门、第三方评估机构等监管主体的视角，对珠三角主要科研事业单位的科技创新能力进行综合评价，以期帮助监管机构在科技计划布局、科技项目审批、科技资金分配等方面进行综合决策。

1 科技创新能力综合评价指标体系

科研单位的科技创新能力评价指标体系应体现其创新能力的时效性、先进性、准确性和可比性。霍尔等［22］人强调了科研经费投入在科技创新评估中的重要性；姚笑秋等［23］、廖文国等［24］和陈国宏［25］等人均从创新投入、创新产出和创新环境等角度构建评价指标；谷景亮等［26］人还引入了与科技项目、科技奖项、创新载体相关的指标；郑嘉颖等［27］探索性地提出广东省基金项目绩效评价指标体系。参考当前相关文献，基于研究课题和评价数据的特点，遵从评价指标的科学性、重要性、可行性、导向性原则，结合实际情况，从创新基础环境、科技创新产出能力、科技创新投入程度和科技项目承接能力4 个方面构建科研机构科技创新能力的四级评价指标体系（见表1）。该指标体系既覆盖了科研机构科技创新能力的主要影响因素，又通过分级和赋权的形式体现了不同指标的重要性。其中，人均指标的计算定义均为对应的规模指标与人员规模的比值，比如人均专利申请数为专利申请数与人员规模的比值。此外，定义末级评价指标为不存在下级指标的指标（如项目实际专利申请数等）。

表1 科研机构科技创新能力评价四级指标体系

2 基于多层级指标清洗与聚合的综合评价框架

准确的综合评价依赖于大量的指标构建，因而指标体系的层次关系复杂［28］，但以往的研究往往将此类多级评价问题简化为单层级评价任务，或者仅对某一层级指标设计评价算法而简单处理其他层级指标，不能充分反映多层级指标体系结构对综合评价结果的影响，为此，本研究提出了一种基于指标聚合的综合评价框架，根据数据指标体系将原综合评价问题分解为多个子综合评价任务，从末级指标开始逐层向上聚合，从而得到更精确的综合评价结果；同时设计了一种指标清洗策略，根据评价指标间的统计特性对数据进行清洗，以提升数据质量，增强评价结果的可信度。如图1 所示，本研究提出的综合评价框架包含三层算法：第一层为数据处理层，本研究提出的双流指标清洗算法根据指标间关系提高数据质量从而提升综合评价结果的可信度；第二层为指标聚合层，根据数据指标体系的层级关系，从最末级指标开始逐级向上聚合，上级聚合指标由次级特征的综合评价得分生成，直到生成一级指标；第三层为综合评价层，基于生成的一级指标数据，设定指标权重进行综合评价，输出最终的综合评价结果。

图1 基于指标聚合的综合评价框架

图2 指标聚合算法流程

2.1 末级评价指标数据集

根据综合评价指标体系构建末级指标数据集X。设共有n个待评价对象，每个对象都有m个指标（属性），则原始数据矩阵为：

2.2 双流指标清洗算法

在综合评价任务中，评价数据往往来自多个渠道，数据质量参差不齐，可能存在数据缺失、格式不统一等问题［29］；此外，存在不同评价对象在同一指标上取值差异巨大、指标间相关关系不一致的现象（比如某评价对象指标a与指标b取值差异远大于均值，而指标a与指标c取值差异远小于均值），可能是数据错漏导致的。因此，设计有效的数据清洗算法是必要的。

实质上，指标间的关系是稳定的，可由数据的统计特性反映。因此，本研究提出了一种基于原始数据统计学性质的双流指标清洗算法，根据指标相关性与指标数据间距离关系识别并修正数据中的异常点、极端值，使得数据与指标关系更加相符，从而提升数据质量，增强综合评价结果的可信性。算法流程如下：

步骤1：将原始数据矩阵X标准化，得到标准化后的数据矩阵Z如下：

步骤6：记Pwmin为相关系数矩阵P中最小的w个元素构成的集合，Pw max为相关系数矩阵P中最大的w个元素构成的集合。检验相关系数矩阵中元素ppq是否属于集合Pmini×γ+δ，其中γ、δ为超参数，表示相关系数的检验范围的大小（设定γ=10，δ=10）。比如，d1max检查对应的相关系数ppq是否属于P20min，d2max检查对应的相关系数ppq是否属于P30min。若不成立，进行如下调整：在相关系数矩阵中，假设，那么根据l 特征进行指标清洗；在特征距离矩阵D中，考察判定条件是否成立，若成立，则将调整为：

2.3 指标聚合算法流程

在指标聚合流程中，本研究使用熵权法确定数据指标权重，使用结合TOPSIS 的灰色关联分析法（GRA）进行指标聚合和综合评价。实际上，本研究提出的综合评价框架可适配不同的指标权重算法和综合评价算法。

2.3.1 熵权法

熵权法是根据各指标所含信息有序程度的差异性来确定指标权重的客观赋权方法，仅依赖于数据本身的离散程度。主要计算步骤如下：

步骤1：根据标准化后的数据矩阵Z计算各指标的熵值。即

2.3.2 结合TOPSIS 的GRA 综合评价方法

TOPSIS 法对数据分布及样本量没有严格限制，只要求各效用函数具有单调性，数据计算简单易行。作为一种常用的组内综合评价方法，TOPSIS 法能充分利用原始数据的信息，精确地反映各评价方案之间的差距。而GRA 法根据有限评价对象与参考序列几何关系的比较，计算参考数列与各评价对象之间的灰色关联度，计算量较小，通常能够与定性分析的结果吻合。因此，结合TOPSIS 的GRA 法，综合了上述两种方法的特点，能够耦合距离相似度和形状相似度进行综合评价。算法流程具体如下：

步骤1：记数据清洗后的综合评价数据集为X，其中n个待评价对象，每个对象都有m个指标（属性）。

步骤2：原始数据正向化。TOPSIS 法使用距离尺度来度量样本差距，需要对指标属性进行同向化处理。通常将指标转化为极大型（期望指标值越大越好）或极小型指标x（期望指标值越小越好），正向化后为x'。即

式（10）中：M为指标x可能取值的最大值。对于中间型指标x，正向化x'为

式（11）中：m为指标x可能取值的最小值。

对于区间型指x，正向化后x'为

式（12）中：［a,b］和［a*,b*］分别为指标x的最佳稳定区间和最大容忍区间。

步骤4：构造标准矩阵Z。即

步骤5：确定最优方案及最劣方案。其中，最优方案Z+由Z 中每列元素的最大值构成，即

步骤6：计算各评价对象与最优方案、最劣方案的距离相似度。即

步骤8：规范化各评价对象与最优方案、最劣方案的距离与关联度。具体表达形式分别如下：

步骤9：计算各评价对象与最优方案、最劣方案的综合关联程度。表达形式分别如下：

步骤10：计算各评价对象与最优方案的贴近程度，作为该评价方案的综合评价得分。即

2.3.3 指标聚合

3 科技创新能力综合评价与分析

本研究基于四级科技创新能力综合评价指标体系，应用多层级指标清洗与聚合的综合评价框架，从监管主体的视角对珠三角地区214 家主要科研事业单位的科技创新能力进行了综合评价。

3.1 数据来源

依托于深圳市科学技术创新委员会平台和载体专项项目（国际科技信息中心）的支持，通过政府官方渠道、调研访谈和次级数据形成研究数据资料。其中，政府官方渠道，即查阅地区的财政、科技管理等部门的相关资料和政策文件等；调研访谈，即实地走访受资助机构、相关受益人员，发放调查问卷并现场访谈；次级数据，即从政府公示网站和媒体新闻中公开的工作报告、公示栏及工作报告等查阅科技专项资助情况。数据时间周期为2016—2021 年。

3.2 指标清洗

从表2 的两个实例来看，省级重点实验室数量和项目实际新增的就业人数得到了修正。可见，本研究提出的双流指标清洗算法能够智能、精准地识别并修改数据异常点、错漏值。

表2 样本单位指标清洗实例

从表3 可知，在样本指标形成的距离矩阵中，省级重点实验室数量和本科及以上人员占比距离最大，而其相关系数为-0.139，不满足检验范围要求，应当调整；而项目实际新增的就业人数和项目实际培养技术工人数距离最小，其相关系数为0.193，不满足检验范围要求，应当修正。

表3 样本单位部分指标距离矩阵

从图3 可知，出版科技著作数与省级重点实验室数量的相关系数最大，而出版科技著作数与省级重点实验室数量的距离（1.004 9）不满足判定条件，因此需修正省级重点实验室数量的数值；由于省级重点实验室数量大于均值1 倍标准差，故调整为1.00（标准化后指标均值均为0，标准差为1）。同理，项目实际培养工程师数与项目实际培养技术工人数的相关系数最大，而项目实际培养工程师数与项目实际培养技术工人数的距离（0.002 2）不满足判定条件，因此调整项目实际培养技术工人数的数值；样本项目实际培养技术工人数的数据点小于均值，且距离小于1 倍标准差，因此调整为-0.03。

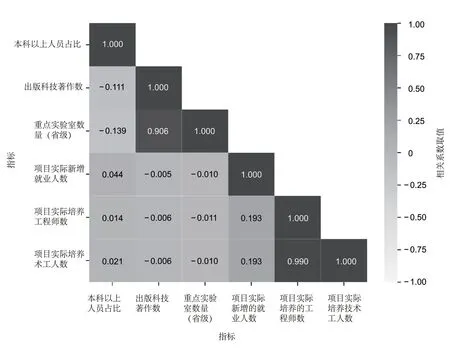
图3 样本单位特征数据集部分指标相关系数

双流指标清洗算法使得修正后的数据点更加符合标准正态分布，一方面能提升数据质量，降低数据错漏点的影响，另一方面能在一定程度上抑制异常值的偏差程度。图4 给出了这两个数据点清洗前后在数据分布中的变动，其中空心四边形点代表修正前数值，实心三角点代表修正后数值。

图4 标准化后样本单位指标数值概率分布

3.3 指标聚合

本研究提出的指标聚合算法可以依据指标数据分布和指标层级关系进行多级指标智能聚合。在保留原始数据信息的前提下，指标聚合得到的任一指标取值是精确的综合评价量化分值，可以在横向（不同评价对象）和纵向（不同评价时间）进行比较分析，提供直观、客观、精确、可量化、可对比的综合评价信息。

3.3.1 实例分析

标准化后使用熵权法计算科技创新奖项对应3个次级指标的权重，结果如表4 所示；然后，应用结合TOPSIS 的GRA 综合评价方法进行指标聚合，指标聚类取值分布如图5 所示。可知，科技创新奖项取值范围为［0,1］，均值为0.377，标准差为0.100，取值分布形态与次级指标相似。

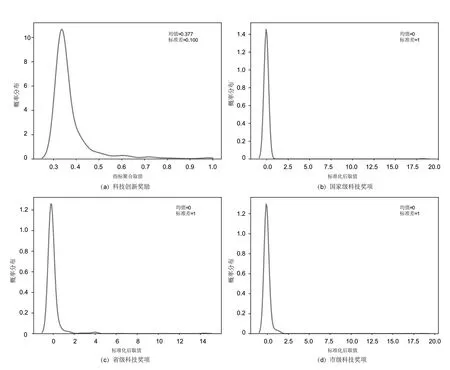
图5 样本单位科技创新奖项指标聚合取值概率分布

表4 标准化后样本单位科技创新奖项指标权重

科技创新奖项得分反映科研事业单位在科技创新奖项方面的综合评价分值及其相应的位次顺序，表5 展示了2021 年科技创新奖项取值最大的5 家机构。其中，机构A1 在科技创新奖项上表现优异且远超其他事业单位；而机构A2 在科技创新奖项这一指标的综合评价得分不断提升，具体如图6 所示。

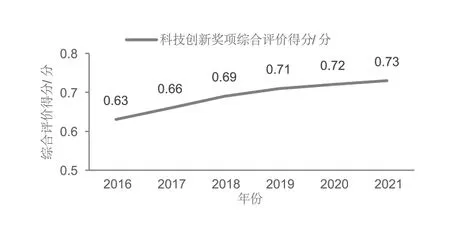
图6 机构A2 科技创新奖项指标得分年度分布

表5 2021 年样本中科技创新奖项综合评价得分前五的单位

3.3.2 一级指标

图7显示了样本单位的4个一级指标取值分布，均呈现右偏分布的形态，且均值在0.47 左右，标准差小于0.20。根据指标聚合算法获取待评价对象的一级指标取值，各二级指标权重如表6 所示。

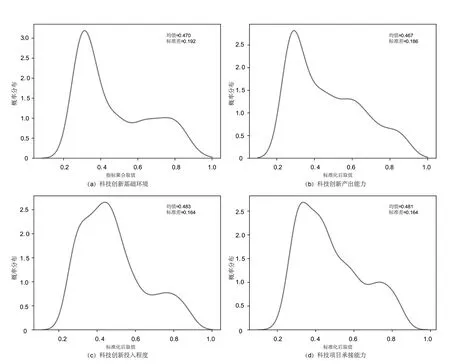
图7 样本单位的一级指标取值概率分布

表6 样本单位的二级指标聚合权重

3.4 综合评价结果

本研究构建的综合评价模型能够客观地对科研型事业单位的科技创新能力进行量化综合评价，样本单位的4 个一级指标综合评价的影响权重如表7所示；图8 则展现了科技创新能力综合评价分值分布，其取值范围为［0,1］，均值为0.49，标准差为0.17，整体呈右偏形态，偏度为0.55，中位数为0.46，分布整体较为平缓，峰度为-0.74。从数据分布来看，主要科研事业单位在科研创新能力上总体存在较大的差异，强弱对比明显。其中，50%的单位综合评分在0.35～0.61 分之间，表明大部分单位的科研创新能力还需要提高；25%的单位综合评分低于0.35分，可认为这些单位的科研创新能力较为薄弱；而综合评分高于0.61 分的单位分布不均，说明头部科研事业单位存在显著的科研创新能力差异。

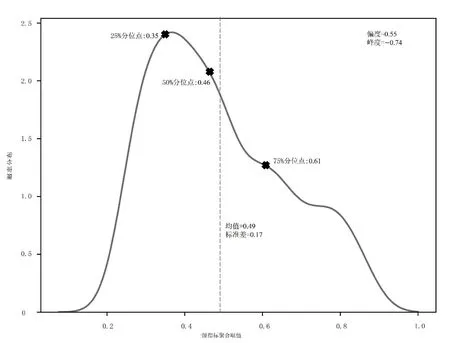
图8 样本单位科技创新能力综合评价得分概率分布

表7 综合评价模型的一级指标权重

基于模型输出的综合评价结果，能够进行整体分析、分档管理、横纵向比较、变化趋势剖析、关键因素定位、提出发展建议等。此外，针对固定的综合评价任务，多层级指标清洗与聚合的综合评价框架可自动定期地运行，提升科技评价效率，节约人力和时间资源。

3.4.1 历年变化情况

为更好地说明样本单位的科技创新能力综合评价结果，将评价框架输出的综合评价分值xi进行变换，表达形式如下：

本研究重点分析了每年综合评价得分排名前50位的机构（以下简称“重点评价对象”）历年变化情况，具体如图9 所示。可知，珠三角主要科研事业单位整体科技创新能力近5年处于稳步增长阶段，于2021 年达到峰值（其中2018 年分值下降主要因为数据量大幅减少）。具体来看，4 个一级指标综合得分范围相近，其中科技创新投入程度进步最为显著，科技创新产出能力和科技项目承接能力上升明显，而科技创新基础环境有所波动、整体提升不显著。另一方面，多层级指标清洗和聚合的综合评价框架对评价对象的分辨率较好。其中，处于Top 2、Top2～Top10、Top10～Top20、Top20～Top30及Top30～Top50 排名的单位的创新综合得分存在明显差异，其中Top2～Top10、Top10～Top20、Top20～Top30 单位的科研创新综合得分增长迅速，而Top2 机构的得分增长稍显缓慢。

图9 珠三角主要科研事业单位科技创新能力综合评价得分

聚焦珠三角地区科技创新事业单位历年综合评价得分排名前十的机构（以下简称“Top10 机构”）（见图10），近5 年间仅有13 所，可见珠三角地区科技创新头部事业单位格局大体比较稳定，其中机构G1和G2稳居前两位，是科技创新的排头兵；机构G6和G8科技创新综合评价分值以及排名均有长足的进步，是新兴科技创新力量。

图10 Top10 机构的年度科技创新综合评价分值

图11 机构G8 的科技创新能力得分

3.4.2 重点机构分析

由图 11 可知，机构G8在近5 年科技创新能力提升显著，在珠三角主要科研事业单位中的排名不断提高，成为科技创新主体中不可忽视的部分；且其科技创新投入程度不断加强，创新基础环境改善明显，科技创新产出能力不断增强，但科技项目承接能力提升不明显，科技创新产出能力仍然存在较大的上升空间。

由图12 可知，机构G6和G8科技创新能力生长的路径不同：科技创新投入程度的提升是机构G6科技创新能力增长的主要推动因素，而机构G8的科技创新产出能力更为突出。

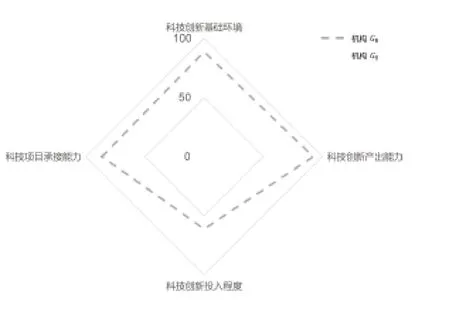
图12 2021 年机构G6 和G8 的科技创新能力对比

4 结论

针对科技创新能力评价任务，本研究提出了一种多层级指标清洗与聚合的综合评价框架，将原综合评价问题分解成多个子综合评价任务进行指标聚合，并设计双流指标清洗算法，基于数据统计学性质增强整体综合评价结果的可信度；并在这一框架指导下，对珠三角主要科研事业单位的科技创新能力进行了定量综合评价，结果表明，基于该方法可以有效揭示珠三角地区不同创新主体的主要优势、发展态势、创新潜力以及薄弱之处。得到的主要结论如下：（1）珠三角地区主要科研事业单位在科研创新能力上总体存在较大的差异，整体科技创新能力近5 年处于稳步增长阶段，但仍有进一步的提升空间；（2）各单位的科技创新投入程度提升显著，科技创新产出能力和科技项目承接能力也明显上升，但整体科技创新基础环境仍有待改善；（3）科技创新头部事业单位格局比较稳定，新兴头部科技创新事业单位的成长路径不同，宜根据自身特点强化优势补足劣势。

另外，本研究提出的综合评价算法框架可以灵活搭载其他不同的综合评价算法，以应对各类科技创新综合评价任务和其他综合评价任务，构建自动化的综合评价模型，对评价对象深入分级分析，定位劣势、强化优势，发挥评价活动“指挥棒”的作用，进一步助力智慧服务、智慧监管、智慧决策和政府数据化转型，赋能科技创新发展。