无人驾驶项目CC-TCMS通信中断场景探讨及优化

夏振东，胡 欢

（卡斯柯信号有限公司，北京 100070）

随着轨道交通行业的不断发展，无人驾驶项目已先后在多个城市投入运营，并且多地正有条不紊的推进着无人驾驶项目的建设，无人驾驶和车-车通信已经成为当今轨道交通行业的热点。无人驾驶项目在场景文件中描述了全自动运行系统在运营中所要处理的场景，包括正常运营场景和非正常运营场景，所描述的对象涉及组成全自动运行整个体系所包含的（子）系统和人员。各个系统遵循场景文件执行，是保障无人驾驶项目功能实现的前提。本文就无人驾驶项目可能会遇到的CC 与TCMS 通信中断的故障场景，论述既有项目此种场景下的处理方式，并基于现有处理机制提出优化建议。

1 FAO项目当前处理及分析

对于CC 与TCMS 通信中断后的处理方式，笔者对比了北京的《城市轨道交通全自动运行系统规范》（T/CAMET 04017.1-2019)以及上海的《城市轨道交通全自动运行运营场景规范》（T/SHJX0018-2020），两者的处理方式基本一致。

总结如下：当车载监督与车辆TCMS 通信的报文时，若超过规定时间未接收到车辆TCMS 报文，则认为与车辆TCMS 通信故障。

系统处理方式如下：

1）若列车处于非零速，施加紧急制动，车停下后由信号向中心申请进入蠕动模式(Creep Automatic Mode，CAM)，中心进行确认后，列车进入蠕动模式，以既定的限速运行到下一站进行清客操作。

2）若列车处于零速，则直接向中心申请进入蠕动模式，中心授权后方可进入蠕动。

以上处理方式，存在如下问题：

1）由于不区分车速，只要非零速，当CC 与TCMS 通信中断后，一律施加紧急制动。因此在没有提前广播告知的情况下，突然施加紧急制动易造成乘客受伤，给乘客带来不好的出行体验。

2）蠕动模式属于降级后的FAO，为保障安全，因此该模式限速很低，非必要过早地进入蠕动模式，会大大降低运营效率。

2 处理方式优化

笔者认为针对CC 与TCMS 通信中断这一场景，不考虑CC 判断与TCMS 失去通信的过程（不同项目有不同的定义）及CC 和TCMS 的时延。当CC已经判断与TCMS 失去通信后，可根据列车所在位置不同，进行不同的处理。本文按以下3 种情况分别论述。

2.1 列车离站过程中的优化处理方式

如图1 所示，当列车在出站过程中出现CC 与TCMS 通信中断的情况，当车已离开站台D距离后，信号不处理，让车进入区间。当车离开站台，运行距离小于D时，信号输出紧急制动，让乘客可以尽早完成疏散，司机/维护人员可提早人工对故障车进行干预。

图1 列车离站Fig.1 Train departure

对于列车离站过程中CC 与TCMS 通信中断的处理方式，需确保在距离D内列车施加紧急制动，车停下后至少有一个门仍在站台区域里。因此从疏散角度结合车辆参数（车门到车端距离等）和停车点到站台边缘的距离进行分析，列车从启动到紧急制动停车的走行距离需满足如下关系，如公式（1）所示。

车长：取自车辆参数。

停车点（SSP）到站台边缘距离：通过平面图数据获取，取最小值。

最小疏散距离：考虑车辆参数中第一个客室门中心到车端的距离及停车点到站台边缘的最小距离，因此最小疏散距离＝2×车端到第一客室门中心距离＋停车点（SSP）到站台边缘距离。

本文引用某开通项目的具体参数进行计算，引用参数如表1 所示。

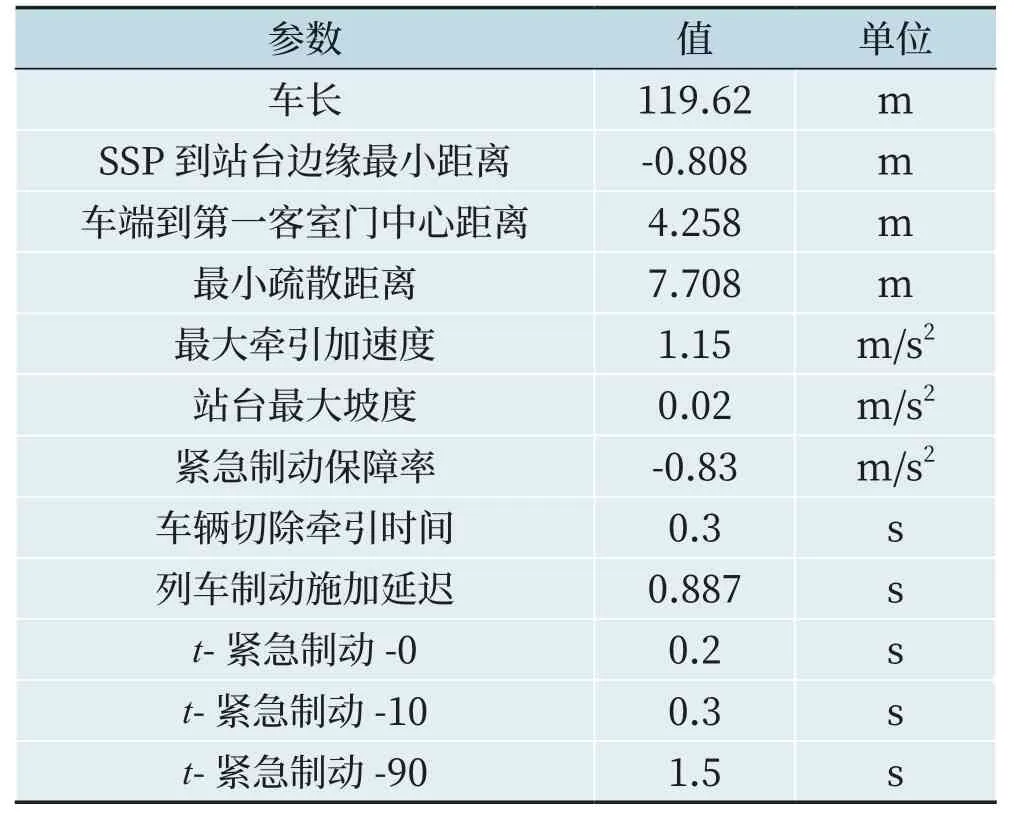
表1 引用参数Tab.1 Reference parameters

因此，总走行距离S＝车长＋停车点到站台边缘距离－最小疏散距离＝119.62 m－0.808 m－7.708 m ≈111.1 m。

从整个运动过程来看，考虑最坏的情况，列车以最大牵引加速度（考虑站台最大下坡）从站台发车，到达距离D时触发紧急制动，随后以紧急制动保障率的减速度（GEBR）进行停车。因此总走行距离S＝D＋紧急制动距离，若要求得距离D，只需求得列车EB 后走行的的距离即可。

对距离D计算过程如下（为方便计算所有计算结果均保留小数点后三位）：

在《CBTC 系统性能和功能要求》（IEEEl474- 1）标准中，为CBTC 模式下列车紧急制动防护模型定义了“典型安全制动速度-距离曲线”，如图2 所示。引入由于列车定位的不确定性(考虑前车定位误差及系统允许范围内可能的退行距离)产生的误差。最外层曲线为该模型下列车不可突破的制动曲线。

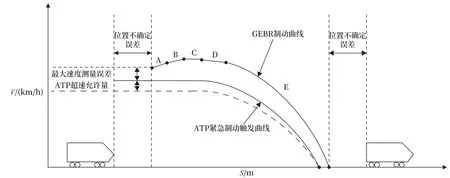
图2 安全制动模型示意Fig.2 Schematic diagram of safety braking model

根据《CBTC 系统性能和功能要求》（IEEE l474-1）标准，可以将紧急制动过程划分为3 个阶段进行评估，如图3 所示。

图3 紧急制动等效模型Fig.3 Emergency braking equivalent model

第一阶段，是车载ATP 系统响应阶段对应图2中的A、B，车载ATP 从检测到紧急制动发生，并触发紧急制动到车辆切除牵引的一段过程。在该阶段t1时间内列车被估算以最大可能的加速度（车辆牵引产生的最大加速度与线路坡度产生的加速度之和）运行。

第二阶段，是车从牵引切除到达到紧急制动保障率的90%的过程，对应图2 中的C、D 过程。对应运行距离、加速度及时间分别为D2、a2，t2；从信号车辆接口电路设计上看，由于车辆牵引切除命令及紧急制动施加命令均采集列车紧急制动环路，因此车辆牵引切除时间与紧急制动施加时间可能有部分重叠。从设计安全角度考虑，在牵引切除过程中应不考虑施加制动的影响。第二阶段的时间t2在时序上应严格滞后于第一阶段时间t1。

根据《列车制动系统性能规范》（EN13452-1），按照如图4 所示等效模型时间参数定义t2的等效延时为te，即通过车辆参数t10和t90计算等效中值te。此时，列车处于惰行状态，安全计算中列车应使用线路坡度产生的最大加速度aslope。

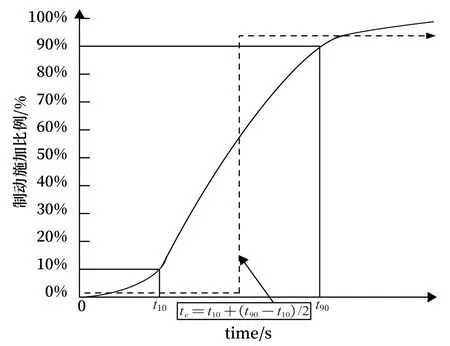
图4 等效惰行延时Fig.4 Equivalent coasting delay

第三阶段是从紧急制动保障率90%的制动施加到列车完全停止的过程。对应图2 中的E 过程。此阶段对应运行距离，加速度及时间分别为D3、a3，t3；本阶段列车处于紧急制动保障率GEBR 施加状态下的全减速状态。

紧急制动3 个阶段对应的运行距离、速度、加速度及时间对应关系如图5 所示。

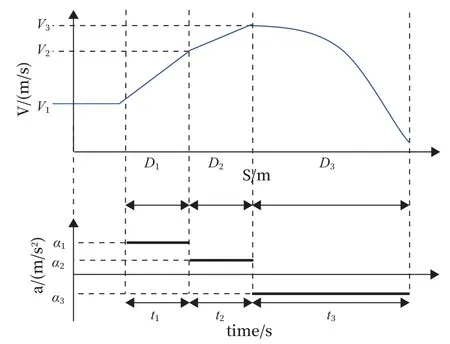
图5 紧急制动模型参数对应关系Fig.5 Corresponding relationship of parameters of emergency braking model

第一阶段中ATP 检测到紧急制动从而进行牵引切除，此阶段列车以最大加速度a1＝1.17 m/s2考虑站台最大坡度加速度为0.02（m/s2）运行，持续时间t1＝1.29 s（考虑系统响应延时及和车辆切除牵引的时间）。根据运动学公式，计算如公式（2）所示。

其中：s表示走行距离；v0表示初速度；t表示时间；a表示加速度。

将相应量带入公式（2），对应运行距离D1＝V1×t1＋0.5×a1×t12，代入已知数值可得D1＝1.29×V1＋0.973。

第二阶段运动相当于惰行阶段，此阶段的时间根据等效惰行延时t2＝te＝（t10＋t90）/2 ＝0.9（s），考虑站台最大坡度加速度为0.02 m/s2，因此此时的最大加速度为a2＝0.02 m/s2，根据运动学公式（2），带入相关量后，运行距离D2＝V2×t2＋0.5×a2×t22＝（V1＋a1×t1）×t2＋0.5×a2×t22，代入已知数值可得，D2＝0.9×V1＋1.366。

第三阶段实际是列车以最小紧急制动aGEBR（即紧急制动保障率GEBR）与线路坡度产生的最大加速度aslope之和，进行匀减速运动停车。通过参数表可知a3＝aGEBR＋aslope＝-0.81 m/s2，根据运动学公式，计算如公式（3）所示。

注：V0：初速度；Vt：末速度；s：走形距离；a：减速度（制动过程）。

将相应量带入公式（3），运行距离可表示为：

根据走行距离关系，S＝D＋D1＋D2＋D3，其中代入数值及表达式可得，0.427×V12＋0.617×V12＋1.885×V1＋1.439 ＋0.9×V1＋1.366 ＋1.29×V1+0.973 ＝111.1，合并同类项后可以得到一个关于V1的一元二次方程，1.044×V12＋4.075×V1－ 107.322 ＝0，根据一元二次方程求根公式，可求得V1＝8.373 m/s，代入可得D＝29.939 m。因此当车出站运行距离在29.939 m 之内，CC 与TCMS 失去通信，列车将施加紧急制动，否则将继续运行。

2.2 列车区间运行中的优化处理方式

如图6 所示，当列车在区间运行过程中出现CC与TCMS 通信中断的情况，此时TCMS 无法接收到信号发出来的牵引制动命令及级位信息。列车受阻力和摩擦力影响自然降速，信号对列车实际车速及参考速度进行监控，具体过程如图7 所示。

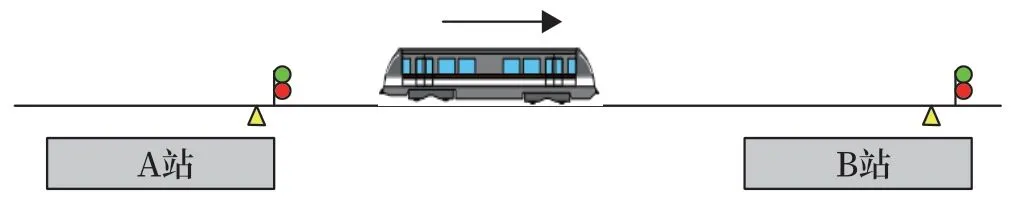
图6 列车区间运行Fig.6 Train is running in the section

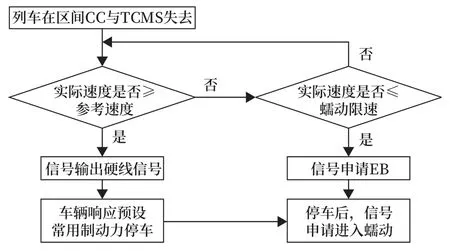
图7 区间运行处理流程Fig.7 Processing flow chart when train is running in the section

若检测到实际速度大于等于参考速度时，信号可输出单独硬线信号或用CAM_OP（蠕动模式可用）替代，车辆非零速收到此信号后施加预设好的一定级位的常用制动力（如-0.6 m/s2）停车，同时播放预制广播（如列车将施加制动停车，请扶稳坐好）。停车后向中心申请进入蠕动模式。

若实际速度小于参考速度，且实际速度小于等于蠕动模式既定速度后，车辆播放预制广播（如列车将施加紧急制动，请扶稳坐好），信号进行干预施加紧急制动，让列车尽快停下来，随后向中心申请进入蠕动模式，中心确认后自动进入蠕动模式，运行到下一站完成清客。

注：可能存在限速区域变化（由大变小），同时存在大下坡，列车响应制动存在一定延时，可能会出现超速EB，此时按正常停车后，申请进入蠕动处理。

2.3 列车进站过程中的优化处理方式

如图8 所示，当列车在即将到站或进站运行过程中出现CC 与TCMS 通信中断的情况，这时需要确保列车能够停在站台，以免发生越站。当列车与站台区域有交集时，CC 根据当前车速，以及距停车点的距离，并依据紧急制动模型，实时进行判断。当CC 确保以当前速度紧急制动后，车能够停在停车点后5 m 内时触发EB。

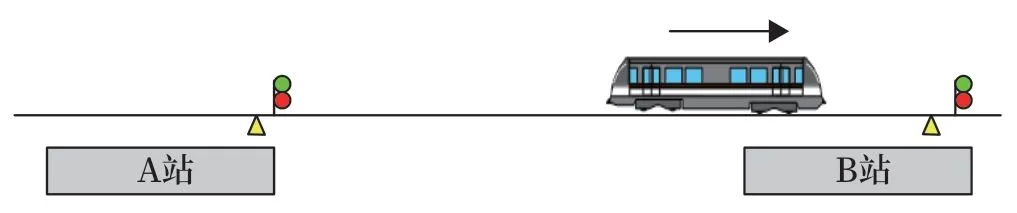
图8 列车进站过程中Fig.8 In process of train entering the station

根据紧急制动模型，紧急制动触发速度即为当前车速，紧急制动距离相当于上文中的D1＋D2＋D3，将变量V1替换为当前速度V，站台区域坡度一般较小，因此统一按表1 中站台区域坡度计算。代入常量，化简后的表达式为D1＋D2＋D3＝0.617×V2＋4.075×V＋3.778。

判定条件如表2 所示。

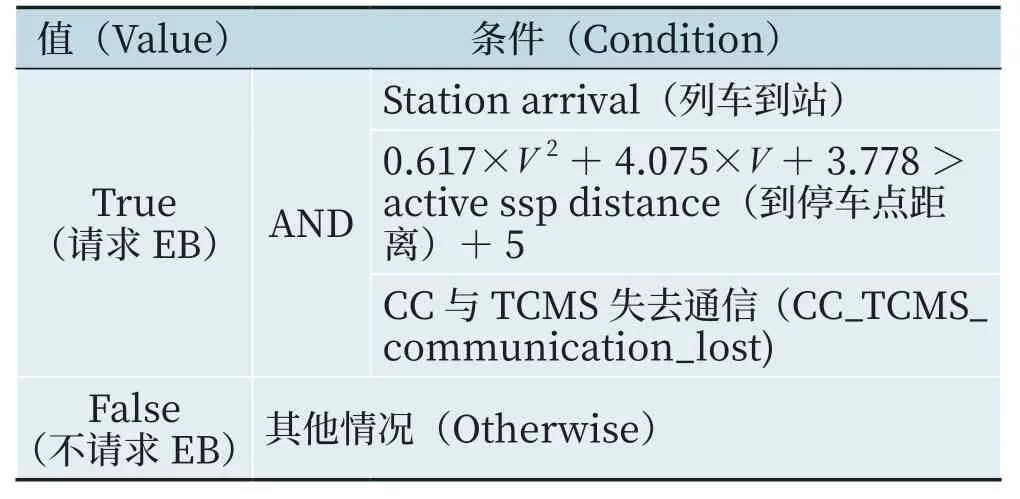
表2 判定条件Tab.2 Determining conditions

增加此判断的目的是，当车进站过程中由于CC与TCMS 通信中断，无法正常施加制动，CC 根据车速实时监控是否需要施加EB 确保列车在本站停车不冒进信号机。同时考虑了跳跃的范围，一旦停车后，正常通过申请进入蠕动模式，在±5 m 范围内，直接通过跳跃进行对标，对标完成后进行清客处理。

3 结束语

随着城市轨道交通行业的不断发展，全自动无人驾驶、互联互通以及车-车通信（TACS）技术已然成为了行业发展的主流，项目在执行过程中也将面临更加复杂的场景。在提高自动化程度的同时，如何更大程度上提高乘客出行体验，当出现异常情况时，如何最大限度减小对运营及乘客出行的影响，是无人驾驶项目需要探究和实现的重要方面。本文通过对CC 与TCMS 通信中断这一故障场景的系统处理进行分析和探讨，给出了笔者认为更加合理的优化方式，希望为后续无人驾驶项目针对此故障场景的系统处理，提供一种新思路。