应答器传输单元滤波性能优化研究
曹鹤飞,孟天旭,杨景博,向 磊
(1.北京全路通信信号研究设计院集团有限公司,北京 100070;2.北京市高速铁路运行控制系统工程技术研究中心,北京 100070;3.北京铁路信号有限公司,北京 102613;4.石家庄铁道大学,石家庄 050043)
1 概论
目前,国内工业化体系不断完善,为适配经济发展与民生需要,对轨道交通运输系统提出更加严苛的要求。列车的运行安全与运输高效主要依靠车载系统与地面系统相互配合实现。其中应答器结构由地面系统中的地面应答器与车载系统中的应答器传输单元主机(BTM)、车载天线3 部分构成,作为车与地之间的信息传输的渠道,保证列车行车环境的安全与可靠,如图1 所示。因其整体分布跨度较大、所处电磁环境十分复杂,服役时会受到各个频段的电磁干扰。如列车弓网离线产生的电弧放电、列车过分相时产生的电弧放电、车载各个电气设备产生的电磁骚扰、雷电产生的电磁脉冲等都会对BTM 接收的信号准确性产生干扰。
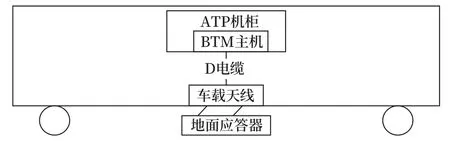
图1 应答器系统组成Fig.1 Balise transmission system composition
本文针对应答器易受电磁干扰的情况,基于电磁兼容三要素,给出通过优化BTM 滤波性能来提高应答器系统抗干扰能力的方案。根据优化后的滤波电路,制作滤波器。实现当BTM 既有的滤波模块无法有效滤除干扰信号时,滤波器可进一步抑制BTM 受到的电磁干扰,最终测试应用本文所示滤波器的BTM 对接收信号过滤效果。
2 轨道电磁环境下应答器系统抗干扰研究
在列车运行过程中,BTM 干扰源如下。
1)分相区的脉冲信号。分相区处在供电区之间且放置绝缘装置。在列车进/出分相区的两个时刻,列车上设备会经历断电与上电,其内电子器件产生脉冲信号并通过空间辐射耦合至应答器。
2)弓网离线的电弧。列车通过受电弓与接触网金属导线的接触实现列车内设备的供电。在实际列车运行中,因受电弓与金属导线之间压力不是恒定值,易出现接触点振荡、受电弓和接触网短暂分离的情况。此时会出现拉弧放电现象,伴随放电产生的高频振荡脉冲通过多条路径耦合至底部设备,影响应答器的正常服役。
3)电气设备的干扰信号。各类设备的线缆在车底铺设的较为紧凑,构造的电磁环境极为复杂。应答器系统的车载天线与D 线缆在此工况下易受各类干扰信号的影响。
目前,铁路系统的应答器规范是基于欧洲制定的应答器技术指标发展而来。部分学者针对轨道电磁环境下的应答器系统做了深入的研究。MariscottiAndrea 等针对受电弓产生的电弧展开相关研究,论述多种降低电弧对列车通信系统产生的电磁干扰的方法;Sharma 团队针对铁路信号设备对应答器传输系统干扰的问题进行相关研究;Y.Ballghllitil 研究了一种特定的评估方法针对来自铁路通信系统外界电磁干扰;Sevillano 团队对BTM系统电磁干扰的信号频率范围进行了相应的分析;V.Deniau 提出用于研究列车电磁干扰的新方法,分析了时域和频域的测试结果;I Adin 分析了应答器系统电磁操作性以及可靠性评估之间的联系。
应答器系统的抗干扰测试,一般采用80 MHz以上频率的干扰信号来进行车载天线辐射抗扰度测试;车载天线与外界实现信息交流的信号频率为3.9 MHz 及4.5 MHz,两个频点均小于80 MHz,天线无法对两个频点附近的干扰信号锁定、抑制。从电磁兼容的三要素考虑,滤波法是常用的抗电磁干扰的方式,在应答器系统中,可通过优化BTM 的滤波性能来抑制电磁干扰。
3 滤波电路的优化及设计
对现有应答器滤波性能进行分析,使用测试系统对列车的应答器系统受扰故障进行模拟。针对现有的滤波问题,设计了一款7 阶椭圆式带通滤波电路。
选取带通滤波器,通过设计时规定其内滤波电路中元器件的参数,实现通过预期频率的信号、抑制干扰信号的功能。设计流程如图2 所示。
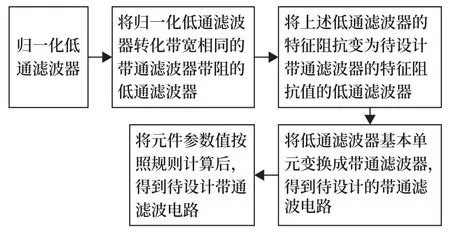
图2 带通滤波器的设计方法Fig.2 Bandpass filter design method
3.1 滤波器的性能指标
3.1.1 滤波器的插入损耗
插入损耗用于表示滤波器抗电磁干扰能力的强弱程度,实际上是滤波器接入后产生的负载功率损耗。插入损耗等于滤波器接入传输系统前经过负载元件的功率与滤波器接入传输系统后经过负载元件的功率的比值,其中dB 表示相对值,表示插入损耗数值。当插入损耗数值变小时,表示滤波器抗电磁干扰能力在减弱,滤波效果越差。插入损耗计算具体如公式(1)所示。
公式(1)中,P1表示为不接入滤波器产生的负载功率损耗;P2表示为接入滤波器后产生的负载功率损耗;U1表示为不接入滤波时的负载电压;U2表示为接入滤波器后的负载电压;Z1表示负载阻值。
除公式运算,网络分析仪直连滤波器也可测出插入损耗。在不考虑符号的情况下,其数值越小,滤波器抗电磁干扰能力越差。
3.1.2 滤波器的反射损耗
将滤波器等效为二端口网络,当其内部阻抗与负载阻抗一致时,滤波器能够保持以最大功率传输信号;当两者不一致时,二端口会反射传输信号。因此在设计过程中,为了抑制干扰信号,需将滤波器内阻与干扰源阻抗设计为互相对冲,以此来反射接收到的干扰信号;设计内阻抗与预期负载的端口阻抗相匹配,以此保证期望信号的不丢失。对此,反射系数可以很好地反应外部设备与滤波器内阻抗的匹配程度,如公式(2)所示。
公式(2)中,Zin是端口外插负载的阻抗;Zs是滤波器本身滤波电路的阻抗。
可以看出,随着反射系数的增大,滤波器反射信号占总体信号的比例会有所上升。
3.2 BTM主机滤波性能
BTM 在接收到车载天线传输的信号后首先是进行滤波。本文对现有滤波电路的S参数进行了测试,测试结果如图3 所示。
当前S 参数测试结果表明,当前内置滤波器的通带过宽。该滤波电路理想工况的中心频率为4.23 MHz,频偏为±283 kHz,实际通带宽大致为3.2 ~4.9 MHz,直接导致了传输单元的接收板无法对干扰信号实现有效的过滤;且因其过度带平缓,通带衰减较大,在-10 dB 左右,减弱了3.9 MHz 与4.5 MHz 两个频点信号的强度,抑制了应答器传输单元对正常报文信息的接收。
用测试系统对列车的应答器系统受扰故障进行模拟,将应答器放置在车载天线下方,使用自制环天线对车载天线施加空间电磁场干扰。观察施加干扰后应答器传输单元面板信号的闪烁情况,如图4所示。

图4 测试设备布置Fig.4 Test equipment layout
在列车行驶过程中,车载天线底面和应答器中心之间的垂直距离一般在22 ~46 cm 这个区间,取22 cm、28 cm、34 cm 这3 个位置点做应答器抗干扰试验。结果如表1 所示。
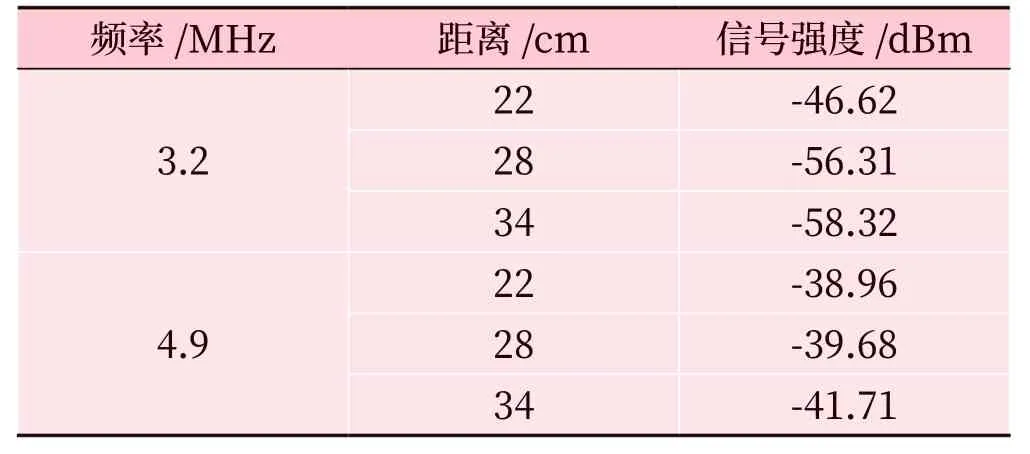
表1 不同频率、距离导致BTM故障对应的能量Tab.1 Energy corresponding to BTM faults caused by different frequencies and distances
由表1 可知,车载天线与应答器中心之间的距离越远,BTM 故障所需要的信号强度越小。
3.3 滤波电路的实现
为尽可能提高应答器系统的抗电磁干扰能力,选取具有较窄通带以及陡峭过渡带的椭圆型带通滤波器。
首先对滤波器进行归一化处理,初步确定滤波器的阶数及元件值,步骤如下:
1)计算低通滤波器的陡峭度系数。在0 MHz~4.8 MHz(fp) 间的波动幅度小于0.2 dB;在以6 MHz(fc)为起点的阻带内,最小衰减为60 dB,如公式(3)所示。
2)查找归一化表。参照估算椭圆滤波阶数曲线,选择在1.3 rad/s 处至少有衰减为60 dB 的椭圆低通滤波器至少为7 阶。
3)确定归一化滤波器元件参数。根据各个元件归一化数据,利用公式对元件参数进行变换,如公式(4)所示。
最终,将所有元器件值乘以系数K,得到7 阶椭圆型低通滤波器各个元器件的设计值。按照低通到带通的电气元件对应关系,在低通滤波电路4 种基本构成单元中找出与之对应的带通滤波电路的基本构成单元,得到椭圆型带通滤波电路,如图5 所示。
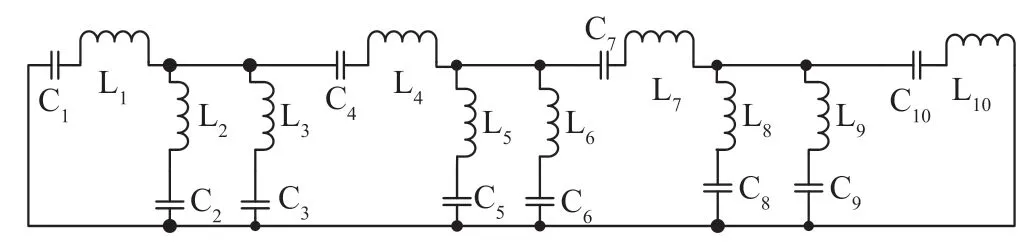
图5 椭圆式滤波电路Fig.5 Elliptic filter circuit diagram
其中,L1、C1串联谐振于4.249 MHz;L2、C2和L3、C3两个串联谐振网络构成了一个并联谐振网络,L2、C2串联谐振于3.624 MHz,L3、C3串联谐振于4.98 MHz;C4、L4串联谐振于4.249 MHz,L5、C5和L6、C6两个串联谐振网络构成一个并联谐振网络,L5、C5串联谐振于3.7 MHz,L6、C6串联谐振于4.878 MHz;C7、L7串联谐振于4.249 MHz;L8、C8和L9、C9两个串联谐振构成一个并联谐振网络,L8、C8串联谐振于3.294 MHz,L9、C9串联谐振于5.479 MHz,C10、L10串联谐振于4.249 MHz。
4 滤波电路的优化
4.1 滤波电路的仿真验证
将本文第三节所得滤波电路导入仿真软件运行,得到插入损耗及反射损耗,如图6、7 所示。
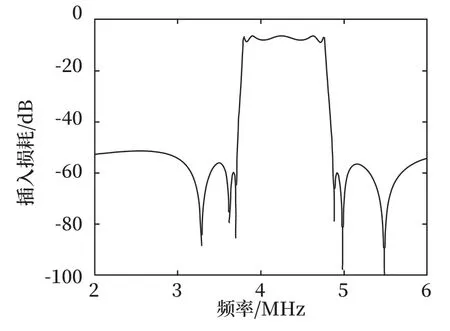
图6 插入损耗参数Fig.6 Insertion loss parameters
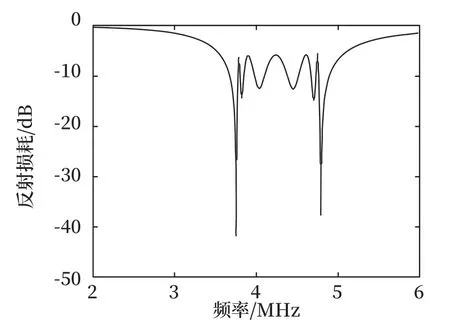
图7 反射损耗参数Fig.7 Reflection loss parameters
软件仿真得到的该带通滤波电路的截止频率为4.78 MHz。可见由传统方法计算得到电路,其实测参数与设计计算时存在明显偏差。
4.2 滤波电路的设计优化
如何使设计时预期与设计运行下的工况一致的问题是多目标、非线性的,各个目标相互制约、相互作用,不可能使所有目标函数达到最优解,通过折中权重等方式让结果能满足设计要求。本文选取3 个目标函数和多个决策变量,来构成滤波器的多目标优化问题。其中多目标优化问题可由公式(5)所示。
公式(5)中,x为决策变量;x=(x1,x2,x3...xn)为决策参数构成的决策变量;z=(z1,z2,z3...zn)为目标函数表达式;gi(x)为约束条件。
NSGA-II 算法是一种用于解决多目标优化问题的方法,它利用非支配排序来对种群中的个体进行排序,通过计算同一等级内个体之间的拥挤距离来保持种群的多样性。该算法比较个体之间的优势和劣势,以逼近一个解决方案,同时在满足终止条件时结束。NSGA-II 采用精英策略,保留了最佳个体,增强了搜索空间。这些特点提高了该算法在解决多目标优化问题时的效率和效果。算法流程如图8 所示。
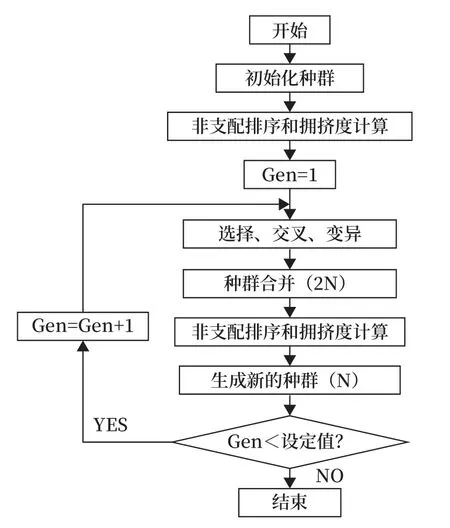
图8 算法流程Fig.8 Algorithm flowchart
NSGA-II 算法从插入损耗、反射损耗以及群时延这3 部分入手,优化了原设计滤波电路的性能。具体要求插入损耗不低于-11 dB,反射损耗不高于-39 dB,并限制4.8 MHz 的群延迟不超过0.13 μs。
将优化后的电路重新仿真,并与优化前的结果进行对比,如图9 ~11 所示。
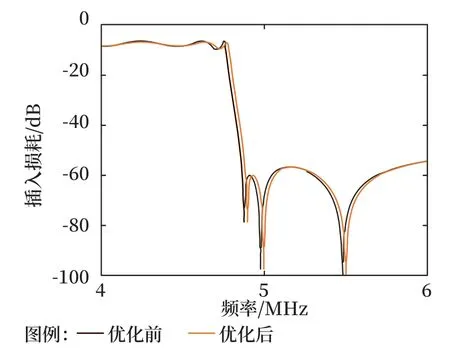
图9 优化前后插入损耗对比Fig.9 Insertion loss comparison before and after optimization
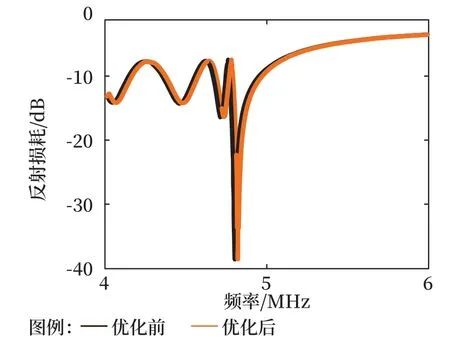
图10 优化前后反射损耗对比Fig.10 Reflection loss comparison before and after optimization
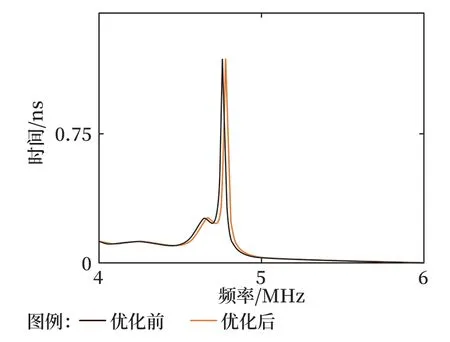
图11 优化前后群时延对比Fig.11 Group delay before and after optimization
仿真论述的是理想状态下的电路。在电器元件实际运行时,电路元件和传输线之间的寄生效应是不可控的,会对滤波器本身运行造成一定影响。为准确地设计滤波器,必须考虑这些因素的影响,并在电路模型中加入传输线以及实际元器件,等效滤波电路如图12 所示。
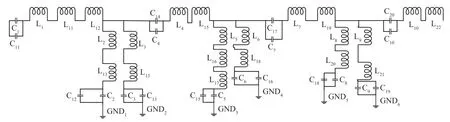
图12 替换元件值后的滤波电路Fig.12 Filter circuit diagram after replacing component values
对等效后的滤波电路进行插入损耗的仿真验证,结果如图13 所示。
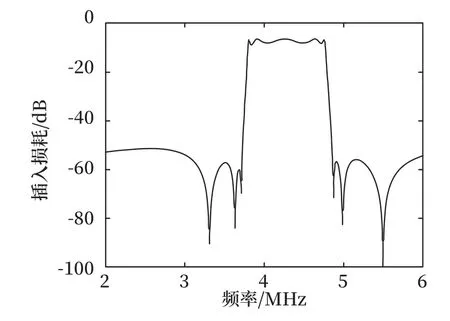
图13 等效后滤波电路的插入损耗参数Fig.13 Insertion loss parameter diagram of filter circuit after equivalence
对比可得,等效前后仿真结果匹配性良好,将元器件进行等效并没有影响滤波电路的性能。考虑实际元器件参数受频率的影响,选择将TDK 的元器件库导入仿真软件的元件库中进行仿真,仿真计算得到的插入损耗如图14 所示。
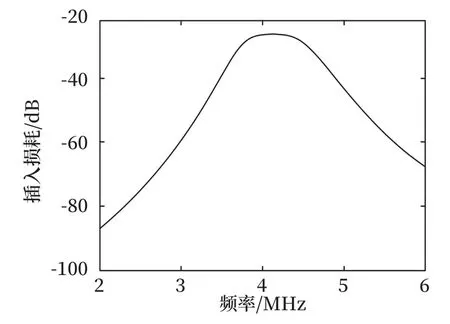
图14 PCB板插入损耗Fig.14 PCB insertion loss
结果表明,实际插入损耗与设计时存在一定偏差,需进行优化。
在仿真软件自带的OPTIM 选择器中选择随机优化器,设置各频段优化目标:3.82 ~4.78 MHz,S21 ≥8.2 dB;2 ~3.7 MHz,4.88 ~6 MHz,S21 ≤53 dB。规定每个元器件实际生产中可以取值的范围。最后通过软件优化得到滤波电路实际生产时的元器件参数。代入新参数后,进行仿真验证,如图15 所示。
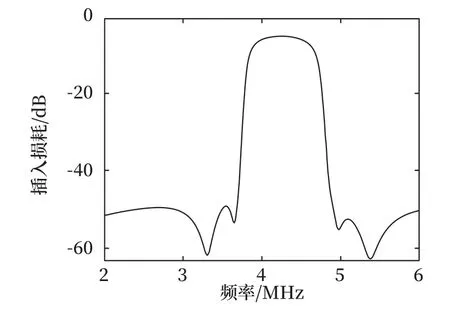
图15 插入损耗的仿真验证Fig.15 Simulation verification of insertion loss
可以看出,上述仿真得到的仿真数据与原理图的仿真数据存在一定的差异,但在通带、过渡带以及阻带仿真数据满足设计要求。这主要是因为通过该软件优化得到的滤波电路的插入损耗仿真与原理图仿真得到的插入损耗,其两者之间算法不同。
4.3 滤波器的制作与参数验证
按照上述章节优化等效的滤波电路图,制作滤波器实物,如图16 所示。

图16 七阶椭圆带通滤波器实物Fig.16 Physical diagram of a seventh-order elliptical bandpass filter
使用型号为N9917A 的安捷伦网络分析模块进行测试,将起始频率设置成2 MHz、终止频率6 MHz,采样401 点。在相同状态下,对比测试了选用既有滤波器和七阶椭圆带通滤波器时天线端口接收的频谱波形,如图17 所示。
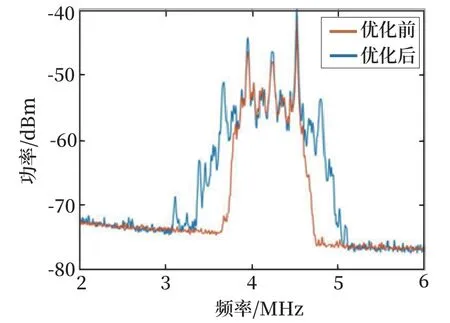
图17 滤波性能优化前后频谱波形对比Fig.17 Comparison of Spectral Waveforms before and after Filtering Performance Optimization
可以看出,该滤波器可以较好地复现理论计算下的设计参数。对按传统计算方法设计的滤波电路进行了仿真验证并提出不足。在此基础上结合NSGA-II 算法,对参数选取进行改进,并据此设计了可实际组装的等效滤波电路,利用软件针对其分布参数等因素进行了参数的仿真优化。
5 总结
本文介绍了应答器系统工作环境的复杂,提出通过优化应答器传输单元的滤波性能,来解决应答器系统的电磁干扰问题的方案。选取合适的滤波电路种类,设计出满足理论要求的滤波电路,然后针对传统方法得到的滤波电路存在误差的问题,提出利用多目标遗传算法来优化滤波电路,同时完成了实物滤波器的等效滤波电路。并针对分布参数的影响因素完成了元件参数优化选取,最后制作滤波器实物,进行实验验证,为后续应答器系统电磁干扰问题的解决提供参考。

