最大化电力系统频率最低点的并网风电机组频率支撑控制
张宇博,杨松浩,郝治国
(西安交通大学电气工程学院,陕西省西安市 710049)
0 引言
经电力电子变流器并网的风机转速与系统频率是解耦的,风机的大规模并网显著削弱了系统的惯量水平[1]。相较于以同步电源为主体的传统电力系统,低惯量电力系统的频率稳定问题凸显,严重威胁电网安全运行[2]。因此,亟须挖掘系统频率控制潜力,增强频率稳定能力。
作为换流器型电源,风机控制灵活、可塑性强,具备为系统提供频率支撑的能力。通过对控制结构进行适当改造,风机能以释放转子动能的方式为系统提供频率支撑,而无须减载备用。这种基于转子动能的风机频率支撑控制最早于2006 年由Johan Morren 等学者提出[3],其基本思想是在风机的原有有功参考值上附加一个与系统频率变化率(rate of change of frequency,RoCoF)dΔf/dt和频率偏差Δf成正比的附加功率,迫使风机响应系统频率变化。这种模拟同步发电机频率响应特性的控制思路因其原理简单、易于实现,得到了广泛的研究和应用。文献[4]以同步发电机和风机组成的两机系统为例,研究了采用惯量控制的风机对系统频率响应(system frequency response,SFR)的实际贡献,以及风机出力水平、控制参数等对系统频率响应的影响。文献[5]指出,不合理的惯量-下垂控制参数可能造成系统频率的二次跌落。针对经典惯量-下垂控制的不足,国内外学者从参数优化[6-8]、结构调整[9]以及风储协同[10-11]等多个方面提出了改进措施。文献[6-7]根据转子动能裕度自适应调整控制参数,以避免风机转速的过度下降。文献[8]基于模糊控制理论,提出一种同时考虑风机运行工况和系统风电渗透率的自适应虚拟惯量控制,保证了风机在不同工况下可靠的有功支撑。文献[9]通过设计合理的风机转速恢复策略,避免了频率的二次跌落。考虑到储能技术的不断成熟,文献[10-11]进一步研究了储能与风机协同的频率控制策略,以提升系统频率稳定性。
考虑到风机出色的可控性和响应速度,上述基于模拟同步发电机的控制思路在一定程度上限制了风机频率支撑能力的发挥。从提升系统频率稳定性这一核心需求出发,部分研究以优化系统频率轨迹为驱动,探索新能源机组频率支撑控制的其他形态。例如,文献[12]通过控制储能来重塑系统频率轨迹,使得系统受扰后的最大RoCoF 和最大频率偏差满足系统运行约束。考虑到当前较高的储能成本,文献[13-14]以风机为控制对象,构建了基于频率轨迹的优化控制模型,以实现系统频率最低点的最大化。但是,上述研究并未严格论证所提控制策略的最优性。另外,利用粒子群算法一次性求解最优控制模型的全时域解过于复杂,难以兼顾准确度和效率。为提高求解效率,文献[15-16]通过构建风机频率支撑的模型预测控制来优化系统的频率轨迹,将动态的优化控制问题逐点离散为含线性约束的优化问题,大大降低了求解难度。然而,如何选取一个恰当的“预测时长”是具有挑战性的。
针对现有风机频率支撑控制研究中的不足,本文从提升系统频率最低点这一核心需求出发,探索风机的最优频率支撑控制。首先,从能量视角严格证明了使得系统频率最低点最大化的频率轨迹的通用形态。然后,以最优频率轨迹为控制目标,结合系统频率响应模型逆向推导风机的最优频率支撑控制。通过引入“能量守恒”约束,简化风机最优频率支撑控制的参数求解,并有效避免了系统频率的二次跌落。仿真结果表明,所提最优频率支撑控制能有效提升系统的频率最低点。
1 系统频率及风机动态模型
1.1 系统频率动态模型
在均一频率假设下(忽略频率的空间分布差异),考虑风机频率支撑的系统频率动态可描述为如下的时域摇摆方程[17]。
式中:H和D分别为系统等值惯性常数和阻尼系数;ΔPm为同步发电机的调频功率;ΔPw为风机的调频功率;Pd为功率扰动量;Δf为频率变化量。
同步发电机的调频功率可计算如下:
式中:Gg(s)表示同步发电机调速器系统的频率响应模型,可以采用等值的单机聚合模型[18]或详细的多机模型[19]。
在本文中,为便于分析和计算,采用经典的基于单机等值的再热模型,即
式中:R为系统一次调频的等值下垂系数;Km为同步发电机的额定功率因数;TR为再热时间常数;FH为高压缸发电比例。对于多机系统,上述等值参数可以通过按容量加权的方式计算得到[20]。
在本文中,风机正常情况下运行于最大功率点跟踪(maximum power point tracking,MPPT)模式,通过释放转子动能为系统提供短时频率支撑,故并不改变系统一次调频的稳态频率。忽略频率响应动态,则一次调频的稳态频率偏差Δfss可计算如下:
尽管不影响一次调频的稳态频率,基于转子动能的风机短时频率支撑可有效改善系统的暂态频率稳定性。这一暂态过程可由如图1 所示的系统频率响应模型来描述。图中:Gw(s)表示风机的频率支撑控制。由于功率缺额扰动在电力系统中更为常见且后果更严重,本文重点关注大功率缺额下一次调频时间尺度内的系统频率稳定性,而频率最低点体现了系统频率稳定的最坏情况,是系统频率响应的重要指标。因此,本文以最大化系统频率最低点为目标,探索风机的最优频率支撑控制,即Gw(s)的最优形态。
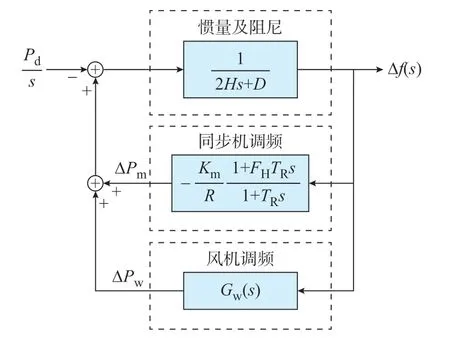
图1 考虑风机频率支撑的系统频率动态模型Fig.1 Dynamic model of system frequency considering frequency support of wind turbines
1.2 风机动态模型
考虑到一次调频的时间尺度在分钟级内,可以忽略这一暂态过程中的风速变化[21],即假定风速在风机短时频率支撑过程中保持不变。同时,采用单质量块模型来描述风机旋转部件的动态特性,即
式中:J为风机旋转部件的惯量;ωr为风机转速;Pw为风机的电功率;Pa为风机的气动功率,其计算公式如式(6)所示[22]。
式中:ρ为空气密度;r为风轮半径;vw为风速;λ=rωr/vw为叶尖速比;β为桨距角;Cp(λ,β)为风能利用系数。
频率支撑过程中,风机的电功率可表示为:
式中:Pw0为风机的初始稳态功率;t0和tf分别为风机频率支撑的起始时刻和结束时刻。本文中,tf被称为“终态”,表示风机短时频率支撑的终止,但这并不意味着系统的一次调频到达“稳态”。为不失一般性,记t0=0。
2 最优频率轨迹形态及其通用性证明
与已知控制模式的参数优化问题不同,若风机最优频率支撑控制的形态未知,则难以直接推导使得系统频率最低点最大化的Gw(s)。因此,本文基于逆向思维来构造风机的最优频率支撑控制,即先推导最大化频率最低点的最优频率轨迹,再通过系统频率动态模型逆向构造使得频率动态呈现期望形态的最优Gw(s)。本章从调频能量角度,严格证明了最大化频率最低点的最优频率轨迹具有如下通用形态:频率以初始RoCoF 速降至最低值,然后保持至终态。下面给出详细证明。
2.1 调频能量最大化原则
风机最优频率支撑控制必须使系统的调频能量最大化,这是使得系统频率最低点最大化的必要条件。下面证明这一原则的合理性。
首先,对摇摆方程式(1)在时间区间t∈[t0,tf]上积分,并假设扰动前频率变化量为0,即Δf(t0)=0,故有
其中
ΔEFR表示系统在时间区间t∈[t0,tf]内释放的调频能量,包含同步发电机和风机;IΔf为频率轨迹在区间t∈[t0,tf]上的积分;Δf(tf)为终态频率偏移。考虑到一次调频是有差调节,故Δf(tf)和IΔf均小于零、ΔEFR大于零。
假设两种不同的风机频率支撑控制下,系统频率动态分别为Δf1(t)和Δf2(t)(t∈[t0,tf])且系统释放的调频能量分别为ΔEFR1和ΔEFR2,不妨设
结合式(8)和式(9),有如下关系成立:
式中:0 <κ<1。
相应地,两种风机频率支撑控制下的系统频率动态满足如下关系:
显然,存在如式(12)所示的频率轨迹,使其满足式(11)中的等式关系,即
记频率最低点为Δfnadir(小于零),则对应两种不同的风机频率支撑控制,有
由式(9)和式(13)可知,风机的频率支撑使得系统释放的调频能量越大时,系统的频率最低点越高。因此,若要使系统频率最低点最优,则风机的频率支撑控制需使系统释放的调频能量最大化,不妨记为ΔE。
2.2 频率轨迹约束
使得频率最低点最大化的频率最优轨迹需满足如下约束条件:最低点频率Δfnadir不低于终态频率Δf(tf)。下面利用反证法来论证该结论。
在系统调频能量最大化原则下,式(8)等号右侧为常数,不妨记为Cmax。因此,最优频率轨迹应满足如下约束:
式中:Cmax=(ΔE-Pdtf)/(2H)。
将满足式(14)但其最低点低于终态频率的频率轨迹定义为次优频率轨迹(如图2 中的蓝色曲线),即
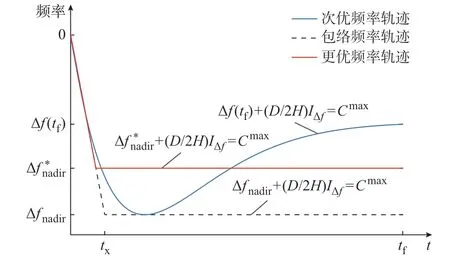
图2 最大调频能量下的频率动态特性Fig.2 Frequency dynamic characteristics under the maximum frequency regulation energy
式中:tc=tf-tx<tf,其中,tx为包络频率 轨迹到达频率最低点的时间。
显然,包络频率轨迹的终态频率偏移和积分与次优频率轨迹之间满足如下关系:
进一步,可得
式中:Cmax和均小于零;0 <η<1。
在包络频率轨迹内,总可以找到与包络频率轨迹具有相同形状的更优频率轨迹,在满足式(14)的前提下,使得频率最低点相较于次优频率轨迹得以提升,证明如下。
更优频率轨迹与包络频率轨迹具有相同的形状特征,即频率以初始RoCoF 速降至其最低点Δf*nadir(图2 中的红色实线),其中,上标“*”表示更优频率轨迹对应变量,下同。为不失一般性,将更优频率轨迹的频率最低点表示为如下形式:
式中:μ表示更优频率轨迹的频率最低点与次优频率轨迹的频率最低点之间的比例系数。
由于均为梯形,通过式(20)所示包络频率轨迹与更优频率轨迹的频率最低点,即图2 中两梯形高之间的比例关系,可以计算得到更优频率轨迹的积分为:
更优频率轨迹的终态频率与轨迹积分需要满足式(14)所示的约束,即
将 式(22)中 的Cmax和 式(18)中 的Cˉ代 入式(19),系数μ可以导出为:
由0 <η<1 可得μ的取值范围为:
其中
当0 <μ<1 时,由式(20)可知:
以上分析表明,若风机频率支撑控制下系统的最低点频率低于终态频率,则必然存在一条更优的频率轨迹,在满足系统调频能量最大化原则的同时,使得系统的频率最低点得到进一步改善。因此,为最大化频率最低点,最优频率轨迹需满足频率最低点等于终态频率。
2.3 最优频率动态
2.2 节证明了最优频率轨迹的频率最低点不应低于终态频率。因此,最大化频率最低点等价于最大化终态频率,即
在最大化系统调频能量原则下,最优频率轨迹的终态频率与频率轨迹的积分之和为一定值,如式(14)所示。因此,最大化终态频率等价于最小化频率轨迹的积分,即
在最低点频率不超过终态频率的约束下,区间t∈[t0,tf]上积分最小的频率轨迹只能是如下形态:频率以初始RoCoF 速降至最低值,然后保持至终态t=tf,即图2 中的红色实线。
除频率均一性假设以外,上述分析和证明过程并未预设风机频率支撑控制的形态,也没有任何其他关于系统参数的限制条件和对于频率响应模型的简化。因此,这一最优频率轨迹的“形态”对于所有含高可控的换流器型电源的电力系统均是成立的,具有普适性和通用性。换流器型电源的作用体现在其功率控制的灵活性赋予了式(1)所示的系统频率动态以一个自由度,从而可以通过自由调节电源出力使得系统频率轨迹呈现出最优形态。
3 风机最优频率支撑控制
3.1 风机最优频率支撑控制的出力特性
尽管最优频率轨迹的“形态”是通用的,但其“数值”即频率最低点仍受换流器型电源的出力特性影响。作为本文的研究对象,风机相较于储能和光伏等有其特殊性。在一次调频时间尺度内,储能的荷电状态可基本认为不受影响。光伏由于没有转动部件,需通过减载备用的方式参与系统调频。因此,储能和光伏均可以在短时调频过程中作为“净释能”的电源。当风机以转子动能为能量源参与系统调频时,其释放的转子动能需快速从系统中回收,否则转速持续下跌会威胁到风机的稳定运行。因为风机的转子动态与系统一次调频动态的时间尺度大致相当,其能量回收特性必须在短时频率支撑控制中加以考虑,从而保证风机转速的恢复,确保风机运行安全。因此,从整个调频时段来看,基于转子动能提供频率支撑的风机是“零释能”的电源,即
式(28)表明,风机在短时频率支撑过程中需满足强制性的“能量守恒”约束,这是其区别于储能和光伏等其他换流器型电源短时调频的关键特性。同时,这一约束保留了足够的灵活性。其灵活性体现在式(28)并未预设关于风机频率支撑控制的具体形式,即ΔPw(t)可以是区间t∈[t0,tf]上积分为0 的任意曲线。
3.2 风机最优频率支撑控制的一般形式
记最优频率轨迹为Δf*(t),t∈[t0,tf],且对应的频率最低点为Δ。为不失一般性,可将其表示为:
式中:α表示比例因子,为大于1 的常数。
如图2 中的红色实线所示,理论的最优频率轨迹是分段函数。为方便推导,本文采用如式(30)所示的指数衰减函数对其进行近似。
近似最优频率轨迹需满足如下频率最低点和初始RoCoF 条件,即
推导近似最优频率轨迹参数如下:
理论最优频率轨迹及其近似结果的对比如附录A 图A1 所示。由图A1 可知,近似最优频率轨迹与理论最优频率轨迹吻合良好,保留了最优频率轨迹的关键特征,且无须分段表示。若不作特殊说明,后文中的最优频率轨迹均表示近似最优频率轨迹。
在已知最优频率轨迹的前提下,将其代入图1所示的系统频率响应模型,可逆向推导出相应的风机最优频率支撑控制。具体地,将式(30)所示的时域最优频率轨迹转换为s域表达式,即
结合图1 所示的系统频率响应模型,可导出式(33)所示的最优频率轨迹对应的风机频率支撑控制函数为:
式中:Kw=(DR+Km)/(αR)-D。
可以看出,风机最优频率支撑控制的作用是与同步发电机调频特性相协同,从而将系统原本呈滞后性的调频特性重塑为无滞后的下垂控制,有效避免了响应滞后导致的频率超调现象,提升了系统频率最低点。附录A 图A2 对比了只考虑同步发电机的系统频率响应和风机-同步发电机协同下的系统频率响应。由图A2 可知,无滞后的下垂控制消除了系统频率的超调现象,从而显著改善了系统频率最低点。同时,系统整体的调频功率需求并未显著增加,甚至略有降低。
从输出功率的角度看,-Kw会使风机产生正的支撑功率,以释放转子动能为代价减缓系统频率的跌落,但会造成风机转速下降;-Gg(s)会产生负的支撑功率,即使得风机输出功率减小以促使风机转速的恢复。当t→∞时,可以忽略Gw(s)中的动态部分,将其近似表示为:
在功率缺额场景下,有Δf(∞)<0。因此,风机的支撑功率ΔPw会变成负值,使其输出功率低于气动功率,从而促使风机的转速恢复。这由式(28)所示的能量守恒约束所保证,不受风电渗透率以及风机运行状态等因素的影响。
3.3 风机最优频率支撑控制的参数求解
式(34)给出了风机最优频率支撑控制的一般形式,其中的参数α未知,其余参数已知。由式(29)可知,α决定了频率最低点的大小,即频率支撑控制的性能。本文利用式(28)的能量守恒约束对α的取值进行求解,具体如下。
由式(33)和式(34)可得风机调频功率为:
风机调频能量为调频功率的积分,由积分的拉普拉斯变换可得风机调频能量的s域表达式,并进一步转换为时域表达式为:
其中
L-1表示逆拉普拉斯变换,ΔEw(t)=∫ΔPw(t)表示风机的调频能量。
根据式(28)所示的能量守恒约束,有
对于给定系统,式(38)是关于风机频率支撑终态tf和比例因子α的非线性二元方程。因此,一旦选定风机频率支撑终态tf,则可以通过求解式(38)得到比例因子α。式(38)所示非线性方程的求解是一个被广泛研究的问题,有很多高效的求解方法[23]以及成熟的商用求解器。因此,在给定tf下求解对应的α是一个平凡问题,本文不作过多叙述。
3.4 风机最优频率支撑控制的具体实现
式(34)表明,所提风机最优支撑控制策略需要系统信息,关于系统参数的辨识和频率响应建模,国内外学者已经开展了大量卓有成效的工作,如惯量的在线估计[24-25]、调速器响应模型的等值建模[18,20]等。因此,本文假定控制中心会在线更新系统信息,即系统模型和参数是已知的。
3.4.1 多风机频率支撑任务分配
在已知系统参数的前提下,控制中心可以快速得到式(34)所示的风机最优频率支撑控制函数Gw(s)。对于含多台风机的系统,控制中心需要将Gw(s)分配到务台风机中,以实现多风机的协同调频。本文考虑如下集中式分配策略:控制中心获取风机的运行状态并评估其调频能力,再根据调频能力将Gw(s)按比例分配到务台风机中,得到第i台风机的控制函数Gwi(s),即
式中:ci∈[0,1]为第i台风机分配系数;N为参与短时频率支撑的风机数量。考虑到转子动能是风机短时频率支撑的能量源,本文采用如下基于转子动能的分配策略,即
式中:Ji为第i台风机的惯量;ωr0i为第i台风机的初始稳态转速。
上述最优控制策略的求解和分配均是基于系统和风机的稳态运行参数,对通信和计算的快速性要求并不高。因此,采用基于控制中心的“集中部署”方式是可行的。在最优控制策略被分配到务台风机后,务风机的频率支撑控制将采用“分散执行”方式,即仅依赖于本地量测频率信息为系统提供紧急频率支撑,保证了响应的快速性和鲁棒性。综上,所提控制策略遵循“集中部署、分散执行”的总体原则。在频率支撑过程中,第i台风机的出力指令Pwi为:
式中:Δfi为第i台风机的本地频率信息。
3.4.2 控制策略的启动与退出
为避免系统正常运行时的频率波动导致控制策略频繁启动,本文采用与同步发电机一次调频类似的频率偏差启动门槛。即只有在检测到系统频率偏差超过预设门槛后,才启动风机的频率支撑控制。此外,由于忽略了风机的气动功率与转速之间的耦合关系,式(28)所示的能量守恒约束无法保证风机在频率支撑终态tf时,转速完全恢复至初始稳态值。因此,需要采取恰当的退出策略以修正这一内在的模型误差,确保风机的状态恢复和安全运行。针对这一问题,本文采用切换至MPPT 控制的频率支撑退出策略,即当风机输出功率降至与MPPT 功率相等时,切换至MPPT 控制,在避免控制切换带来的功率阶跃/骤降的同时,保证风机能完全恢复至初始稳态。因此,尽管tf-to是理论上风机的频率支撑持续时间,能量守恒约束内含的模型误差使得风机实际的频率支撑时间是由MPPT 曲线与输出功率曲线的交点决定的。
考虑启动和退出策略的风机最优频率支撑控制的控制框图如附录A 图A3 所示。在检测到系统频率偏差超过预设门槛后,风机由正常运行状态下的MPPT 控制切换至最优频率支撑控制;在频率支撑过程中,风机的输出功率先增加后减小,一旦检测到输出功率与MPPT 功率相交,则退出策略被激活,风机由最优频率支撑控制切换至MPPT 控制并保持,MPPT 控制下风机转速会完全恢复。
4 仿真验证
4.1 算例1:含单台风机的4 机系统
如附录A 图A4 所示,本文搭建了包含1 台风机的4 机系统来验证所提方法的有效性。该系统的有功负荷为PL=1 800 MW,3 台额定容量为800 MV·A 的火电机组,机组及调速系统相关模型参数见附录A 表A1,系统阻尼系数D=1。等值风机由240 台额定功率为5 MW 的双馈风机构成,基本参数如附录A 表A2 所示,详细模型可参考文献[26],调频启动门槛为Δfth=-0.03 Hz。火电机组出力为1 117.2 MW,风机出力为682.8 MW,风电出力占比为37.93%。在10%的负荷突增(180 MW)下,计算得稳态频率偏差为Δfss=-0.187 5 Hz。此外,考虑系统一次调频的时间尺度一般在十几秒至几十秒,本文推荐风机调频持续时间预设为30 s。设置tf=30 s,由式(38)可得α=1.213,进而代入式(34)得Kw=15.48,推导出风机的最优频率支撑控制函数为:
4.1.1 风机最优频率支撑控制的效果
图3 展示了风机最优频率支撑控制的效果。
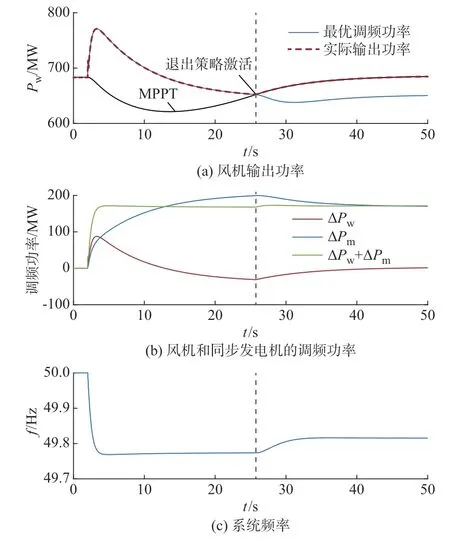
图3 风机频率支撑控制的效果Fig.3 Performance of frequency support control of wind turbines
图3(a)表明,在式(42)所示最优频率支撑控制的作用下,风机在频率支撑初期输出正的支撑功率以改善系统频率稳定性,而后逐渐减小支撑功率以促进自身转速的恢复。图3(b)则详细展示了调频过程中风机与同步发电机调频功率的协同效果。由图3 可知,同步发电机的频率响应呈现滞后特性,功率是逐步增大的,如图3(b)中的蓝色实线所示。风机在扰动初期弥补了同步发电机频率响应的滞后特性,随后逐步减少支撑功率以促使转速恢复,所提控制策略保证了风机支撑功率的下降速度与同步发电机调频功率的上升速度完全匹配,其调频功率的协同效果如图3(b)中的绿色实线所示。因此,风机支撑功率的降低不会产生不平衡功率,从而恶化频率动态。通过这种协同作用,风机的频率支撑控制使得系统频率呈现出期望的最优形态,即系统频率速降至最低值并能保持不变,如图3(c)所示。
当输出功率与MPPT 功率相等时,风机由最优频率支撑控制切换至MPPT 控制,以确保风机转速的完全恢复和后续的稳定运行。可以看出,该退出策略保证了控制切换过程中风机输出功率的平滑性。在MPPT 控制下,风机转速不断上升直至恢复至初始稳态值。相应地,系统频率由频率最低点逐渐过渡至稳态频率。
4.1.2 对比验证
本节对比测试了风机采取固定参数的惯量-下垂控制[3]、自适应惯量-下垂控制[6],以及所提最优频率支撑控制在不同扰动水平下的控制效果,结果如表1 所示。表中:扰动水平定义为扰动量Pd与有功负荷PL的比值(Pd/PL),用于表示扰动的严重程度。此外,为简便起见,分别用C1、C2、C3 代表3 种控制方法。
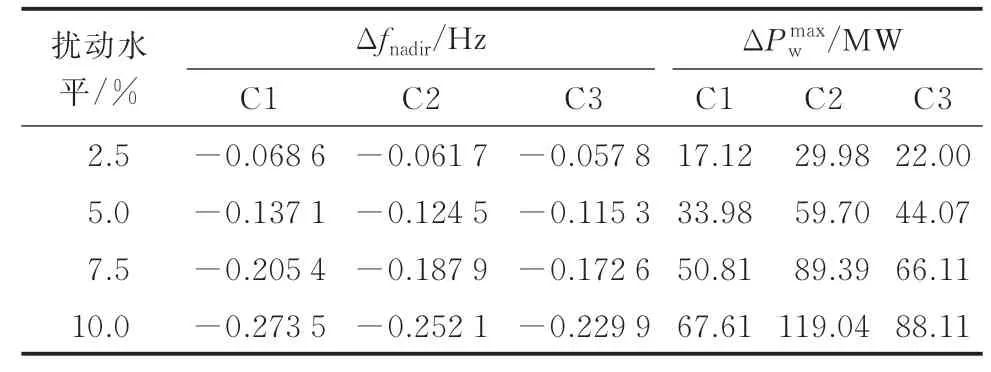
表1 不同功率扰动水平下的控制方法对比Table 1 Comparison of control methods at different power disturbance levels
表1 中,ΔP表示风机支撑功率的最大值,即
式中:P为调频过程中风机输出功率的最大值。
可以看到,在不同扰动水平下,风机采用所提最优频率支撑控制时,系统的频率最低点均高于对比方法,说明所提方法能有效改善系统频率的稳定性。此外,表1 中最后两列的对比结果表明,这一性能提升并非单纯依靠增大风机的支撑功率来实现,所提方法所需的最大支撑功率ΔPmaxw在不同扰动水平下均小于自适应惯量-下垂控制,却实现了更高的系统频率最低点。
以10% 的负荷突增为例,图4 进一步展示了3 种风机频率支撑控制的时域对比结果。以频率最低点的频率偏移为指标,所提最优控制(-0.230 Hz)相较于固定参数的惯量-下垂控制(-0.273 Hz)和自适应惯量-下垂控制(-0.252 Hz)的相对性能提升分别为15.75%和8.73%。所提控制相较于自适应惯量-下垂控制实现了更高的频率最低点,但其最大风机支撑功率需求相较于自适应惯量-下垂控制却降低了26.0%(由119.04 MW 降至88.11 MW),如图4(a)中的红色实线和蓝色实线所示。即所提方法以更小的控制代价实现了更好的控制效果,这充分证明了所提控制的优越性。更重要的是,这一结果揭示了将系统一次调频特性纳入风机频率支撑控制的设计是有益的,或能更充分地发挥风机的调频潜力。
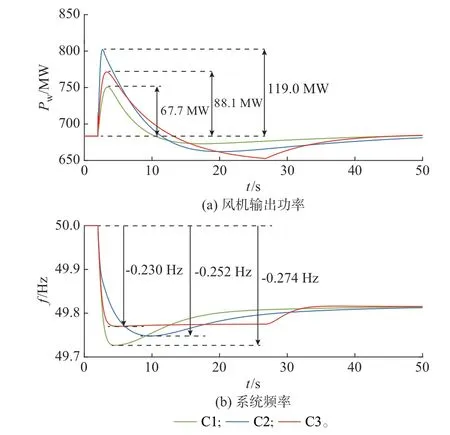
图4 10%负荷突增扰动下的时域结果对比Fig.4 Comparison of time-domain results under a disturbance of 10% load surge
4.1.3 鲁棒性验证
由第3 章的分析可知,系统频率呈现期望最优轨迹的前提是风机的支撑功率需满足式(36)。显然,它与功率扰动量Pd成正比。考虑到实际风机有限的调频能力,所提控制策略只能在一定扰动范围内实现最优频率轨迹,记为Pmaxd,对应的扰动水平PmaxdPL称为扰动鲁棒范围。同时,风机的调频能力会受到风电渗透率和运行风速的影响,进而影响扰动鲁棒范围。为了定量描述不同运行状态下的扰动鲁棒范围,本文定义如下误差指标:
式中:er为实际频率最低点与理论频率最低点之间的相对误差,当er≤5%时,认为扰动水平处于扰动鲁棒范围之内。
图5(a)展示了不同风电渗透率和运行风速下,所提频率支撑控制策略的扰动鲁棒范围。由图5(a)可知,不论风机的调频能力是否充裕,所提控制策略均能承受一定大小的功率扰动,并保证系统频率轨迹为期望的最优形态。同时,当风电渗透率水平超过20%时,对于一般意义上的大功率缺额扰动(不超过总负荷的10%),所提风机支撑控制在一个相当宽泛的风速范围内,均能使得系统频率轨迹呈现出期望的最优形态,具有较好的鲁棒性。
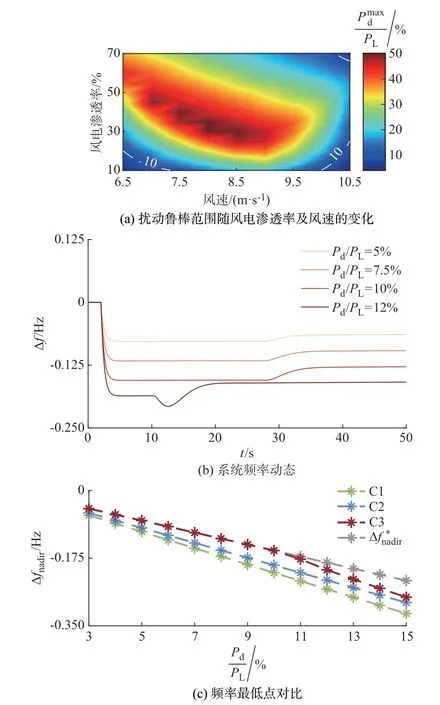
图5 扰动鲁棒性验证结果Fig.5 Verification results of disturbance robustness
图5(b)展示了风电渗透率为20%、风速为6.5 m/s 时,不同扰动水平下的系统频率动态。由图5(b)可知,对低于Pmaxd的功率缺额扰动,所提控制总能使得系统频率轨迹呈现出期望的最优形态。因此,面对实际系统中随机的功率缺额扰动,这一事前整定的控制策略对不超过Pmaxd的功率扰动均可以实现期望的最优控制效果,方法实用性较强。当扰动水平超过Pmaxd时,所提控制仍可在扰动初期保持期望控制效果,随着调频能力被耗尽,风机会退出调频从而导致频率轨迹偏离期望最优形态,即对于超出鲁棒范围的扰动,所提方法的性能会有一定程度的下降。尽管如此,扰动初期的效果保持也能为紧急调度其他调频资源争取时间。
图5(c)进一步对比了在上述低风电调频能力场景下,不同风机频率支撑控制策略下的系统频率最低点。由图5(c)可知,当扰动水平不超过P时,所提控制策略的频率最低点明显优于对比方法;当扰动水平超出P时,尽管所提方法的性能有所下降,但在较大扰动范围内仍略优于对比方法。
4.2 算例2:含多台风机的IEEE 39 节点系统
本文在DIgSILENT/PowerFactor 仿真软件中,搭建了如附录A 图A5 所示的IEEE 39 节点系统模型,以进一步验证所提方法在大规模电力系统中的有效性。仿真系统中包括10 台同步发电机,分别记为G1~G10;调速器则采用如附录A 图A6 所示的IEEEG1 经典模型[27],该模型中包含了同步发电机的调频死区、限幅等非线性特性。同步发电机及调速器系统的具体参数如附录A 表A3 所示。系统总有功负荷为6 097.1 MW,系统阻尼系数D=1。母线3、5、13、21、22 处务接入一台80×5 MW 的等值风机,风机模型与算例1 相同,务风机的风速和分配系数如表2 所示。设在t=2 s 时有500 MW 的有功负荷突增,占总有功负荷的8.2%。
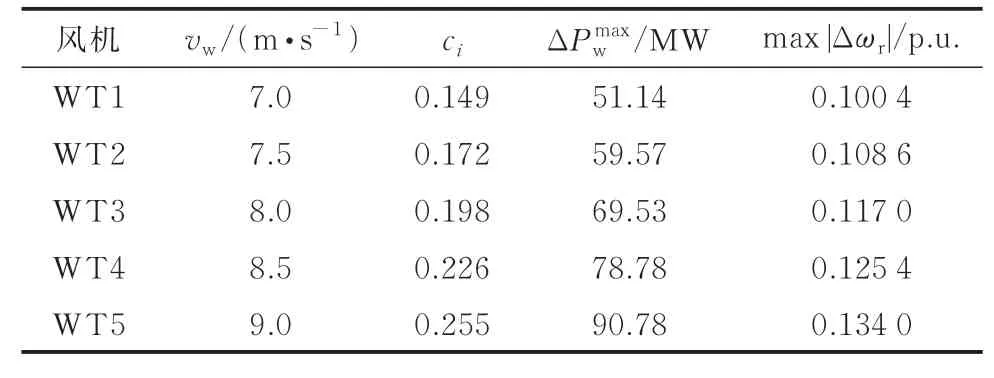
表2 多风机运行条件及频率支撑结果Table 2 Operation conditions and frequency support results of multiple wind turbines
对于上述大规模电力系统,在构建风机的最优频率支撑控制时,可将所有调速器的频率响应聚合为如式(3)所示的简化模型。具体地,在1%的频率阶跃扰动下,测得所有调速器(详细模型)的响应曲线,并加权聚合得到调速系统整体的阶跃响应曲线。然后,借助MATLAB 中的System Identification Toolbox(参数辨识工具箱)[28],以阶跃扰动为输入、聚合的阶跃响应曲线为输出,识别式(3)中的参数,从而得到调速系统的简化模型。对于本文所采用的IEEE 39 节点系统,其简化模型的参数辨识结果为Km/R=17,FH=0,TR=7.69 s。简化模型与详细调速系统模型的阶跃响应曲线对比结果如附录A 图A7 所示。由图A7 可知,简化模型与详细模型的阶跃响应曲线吻合良好,表明简化模型能较好地表示同步发电机调速系统整体的调频特性。需要说明的是,这一简化模型仅用于构造风机的最优频率支撑控制函数Gw(s),在仿真验证中,同步发电机仍采用详细的IEEEG1 调速器模型。同样地,设置风机的频率支撑时间为30 s,根据式(38)可求得α=1.318 7,进而导出风电机组的最优频率支撑控制函数。
在所提最优频率支撑控制和式(40)所示的分配策略下,务风机的输出功率和转子动态如附录A图A8 所示。同时,表2 详细列出了频率支撑过程中,务风机的最大支撑功率和最大转速跌落。其中,最大转速跌落定义如下:
式中:ω为频率支撑过程中风机的最低转速;ωr0为风机的初始稳态转速。结果表明,风速大的风机因转子动能充裕而承担更多的频率支撑任务,表现为更大的支撑功率和转速跌落。
同步发电机转子频率如图6 所示。由图6 可知,对于大规模电力系统而言,由于同步发电机转子之间的功角摇摆,扰动初期频率呈现出一定的空间分布差异,这是大规模多同步机系统的固有特征。所提控制策略无法消除这种暂态振荡现象,但可以看出,系统频率整体仍呈现出期望的一阶特性,表明所提方法对于大规模、非线性电力系统仍然适用,可以有效改善系统的频率稳定性。
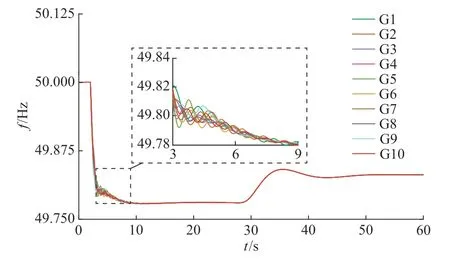
图6 同步发电机的频率Fig.6 Frequency of synchronous generators
5 结语
本文以最大化系统频率最低点为目标,提出了风机的最优频率支撑控制,并通过大量仿真验证了所提方法的有效性,得到如下结论:
1)本文证明了使得系统频率最低点最大化的频率轨迹通用形态,并以此为基础提出了风机的最优频率支撑控制策略。该控制策略使得风机的频率支撑与同步发电机一次调频相互协同,充分发挥了风机的调频潜力,显著提升了系统频率最低点。
2)所提风机最优频率支撑控制策略对于一定范围内的扰动是鲁棒的,这使得所提方法可以避免复杂的实时计算,实用性较强。对于超出风机调频能力的严重扰动,所提方法仍能短时保持期望控制效果,为其他调频资源的调度争取时间。
此外,本文所提方法假设所有同步发电机的调频模型已知,但对于实际大规模电力系统而言,这一假设较为理想。下一步工作将研究在实现风机最优频率支撑控制目标的前提下,利用无模型控制技术,减少或避免对同步发电机调频模型的依赖,提升方法在实际电力系统中的实用性。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

