考虑电压动态的电力系统频率强度量化方法
胡 光,高晖胜,辛焕海,谭 枫,陈可欣
(浙江大学电气工程学院,浙江省杭州市 310027)
0 引言
随着新能源大量接入,以同步机为主导的传统电力系统正在向电力电子化的新型电力系统转变[1]。这将导致系统的惯量、调频能力下降,系统的频率响应性能恶化[2],频率安全稳定问题频发[3-4]。
在分析频率安全稳定问题时,现有分析方法通常基于务节点电压幅值恒定的假设,关注设备的频率和有功功率响应特性[2],然而,系统的频率响应可能受到电压幅值动态(下文简称“电压动态”)的影响。例如,在对“9·19”锦苏直流闭锁事件的仿真研究中发现,事故后快速切除直流滤波器,频率最低点可由49.6 Hz 提升至49.7 Hz,提升约20%[5]。这是由于切除滤波器降低了负荷节点的电压幅值,进而减小负荷消耗的功率,抵消了部分功率扰动。同样,电力系统稳定器 (power system stabilizer,PSS)也会通过改变电压影响负荷的功率,进而影响系统频率[6]。新型电力系统中,电力电子设备的控制设计灵活多样,其中,一些控制方案不再严格按照频率和电压解耦控制,这进一步加剧了系统频率和电压之间的动态耦合[7]。例如,文献[8]为了提升系统的稳定性和动态性能,在跟网型变流器中引入了有功功率-电压(记为P-V)、无功功率-频率(记为Q-F)附加控制。文献[9]将频率动态引入电压控制回路,提出了一种抑制功率振荡的下垂控制方案。此外,混合同步[10]、虚拟振荡器[11]、强同步[12]等控制方案,都采用了电压和频率的综合信号对变流器进行控制。这些控制方案增强了装备内部的频率和电压之间的耦合,可能导致电压动态对系统频率的影响更加明显。
目前,已有一些文献研究了电压动态对系统频率的影响。文献[13]分析了静态负荷的电压特性对系统频率的支撑效果,提出了集合多重惯量形式的广义惯量。文献[14]通过仿真分析了风电低电压穿越对电网频率的影响;文献[15]进一步提出了考虑风电低电压穿越过程的系统频率特征量化方法。上述研究分析了电压动态对频率轨迹变化趋势的影响,能准确给出频率稳定的定性分析结论,但缺乏电压动态对频率影响的定量化分析和机理解释,而且分析结果可能只适用于特定的分析对象。与之相比,基于模型的分析方法能为频率稳定问题的研究提供理论基础,可以进行灵敏度分析,并得到一般性的结论[16-17]。例如,广泛用于系统频率分析的平均系统频率(average system frequency,ASF)模型[18]、系统频率响应(system frequency response,SFR)模型[19]和共模频率(common-mode frequency,CMF)模型[20]等,然而,这些解析模型大多基于电压恒定的假设[18-22]。为了更全面地分析系统频率动态,文献[23]提出了一种同时包含电压和频率动态的“复频率”模型。然而,该模型是在务母线视角下定义的,无法基于该模型得到系统全局频率的方法。文献[24]提出了一种考虑电压影响的CMF 模型,充分考虑了务节点的电压动态,可以用于分析系统的全局频率安全稳定问题。
与振荡失稳等稳定问题不同,频率的安全稳定问题主要关注频率最低点Δωnadir、频率变化率(rate of change of frequency,RoCoF)等系统受扰后的频率响应特征不越限。为定量化分析电力系统的频率安全稳定问题,文献[25-26]提出了频率支撑强度(下文简称“频率强度”)的概念,用于直观描述由电网和设备构成的闭环系统频率响应性能。需要说明的是,系统频率强度是个抽象的概念,具体体现在频率最大偏差量、RoCoF 等系统受扰后的频率响应特征[13,17,22]。目前,系统的惯量、一次调频能力、跌落深度系数等常被用做量化系统频率强度的指标[16,20,26],可 以 用 于 定 量 评 估 系 统 抑 制 频 率 波 动 的能力。然而,上述系统频率强度量化方法未考虑电压动态影响,可能导致设备的频率支撑能力和系统频率强度的量化评估结果不准确。
为此,本文在文献[24]的基础上,提出了一种考虑电压动态的电力系统频率强度量化方法,保留了系统中的电压-频率耦合动态,可以准确量化系统的频率强度。首先,从系统闭环模型出发,建立了考虑电压动态影响的共模频率(voltage-influenced common-mode frequency,VCMF),根 据VCMF 模型中电压耦合项(voltage coupling term,VCT)的表达式,揭示了电压和频率的交互作用回路,并分析了混 合 同 步 控 制(hybrid synchronization control,HSC)构网型变流器、外环附加控制跟网型变流器、静态和旋转负荷等系统元件动态对系统频率的影响。然后,通过电力系统分区,实现了VCMF 模型的简化解耦,进一步利用统一结构传递函数模型,量化了系统整体的频率强度和务区域的频率支撑能力。最后,通过仿真算例验证了VCMF 模型的有效性以及所提量化方法的准确性,并定量化分析了电压-频率动态强耦合案例。
1 考虑电压动态的系统频率响应模型
本章根据雅可比形式的系统闭环模型,在保留电压动态的基础上,通过模态解耦得到系统频率响应中的共模分量。
1.1 系统闭环模型
建立多机系统的线性化模型并消去中间无源节点,得到如图1 所示以ΔPD和ΔQD为输入、以Δθ和ΔV为输出的闭环框图。图中:ΔPD和ΔQD分别为等效至务设备节点的有功功率和无功功率微增量列向量[27];Δθ和ΔV分别为设备节点的相角和电压幅值响应微增量构成的列向量;MG为设备的雅可比传递函 数 矩 阵;MN为 交 流 网 络 的 雅 可 比 矩 阵;GPθ(s)、GPV(s)、GQθ(s)、GQV(s)分别为设备侧有功功率-相角(记为P-θ)、P-V、无功功率-相角(记为Q-θ)和无功功率-电压(记为Q-V)间的传递函数矩阵;LPθ(s)、LQV(s)、LPV(s)、LQθ(s)为对应的网络侧传递函数矩阵;s为拉普拉斯算子。与仅保留有功功率ΔPD和相角Δθ及两者间传递函数矩阵的传统频率分析模型相比,图中的模型进一步保留了无功功率和电压幅值ΔV及对应的传递函数矩阵。
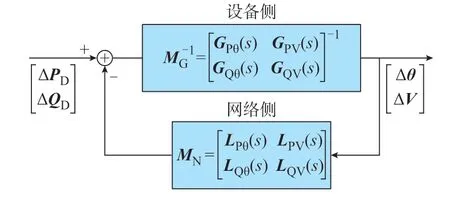
图1 系统闭环传递函数框图Fig.1 Block diagram of system closed-loop transfer function
图1 所示系统的闭环传递函数响应模型可以表示为:
式中:HPθ(s)、HPV(s)、HQθ(s)、HQV(s)分别为设备侧和网络侧动态传递函数矩阵求和得到的P-θ、P-V、Q-θ、Q-V 间的闭环传递函数矩阵。具体模型表达式及模型简化合理性论述详见附录A。
值得一提的是,根据潮流旋转不变性[17],与相角相关的网络雅可比矩阵形式的传递函数矩阵LPθ(s)和LQθ(s)都有一个零特征值,对应的特征向量为元素全为1 的n维列向量E:
1.2 考虑电压动态的系统频率响应模型
对于式(1)中的系统闭环响应模型,采用文献[24]中的模态分解方法可从中提取出考虑电压动态的系统CMF 响应量:
式 中:ΔωVCMF=[ΔωVCMF,1,ΔωVCMF,2,…,ΔωVCMF,n]T,为务设备节点频率响应中的CMF 分量,其中,下标n为系统中设备总数,ΔωVCMF,n为ΔωVCMF中的元素;c∈Rn×1,为权重系数[24],ci为c的元素;GPθ,i(s)为第i台设备的传递函数,i=1,2,…,n;ω0为额定工频频率。
与不考虑电压动态的系统全局频率相比,式(3)中多了一项cT HPV(s)H-1QV(s)HQθ(s)E,将其记为电压耦合项GVCT。当系统中电压不存在波动时,GVCT=0。可以看出,式(3)中频率分量在所有母线上 都 是 一 致 的,有ΔωVCMF,1=ΔωVCMF,2=…=ΔωVCMF,n,符合系统全局频率的典型特征,将其定义为VCMF,记为ΔωVCM。需要说明的是,实际应用中,对于含有聚合负载或者配电网等“黑箱”模型的系统,直接根据黑箱设备并网端口的相角(频率)和有功功率辨识得到等效模型,没有充分考虑电压动态的影响,在频率响应分析时会存在误差,而且这样得到的某台设备等效模型本质上包含了系统中全部设备的动态,在投切机组时要对全部设备重新辨识,不适合工程实际应用。具体分析及等效模型的合理获取方式见附录B。
本章建立了考虑电压动态影响的系统频率响应模型,然而,电压动态通过耦合项对系统频率的具体作用机理尚不清楚,务种设备动态在电压耦合项中的作用也不明确。为此,需要分析电压动态影响系统频率的作用回路以及设备(负荷)动态对电压耦合项的影响。
2 电压动态对系统频率的影响分析
本章首先根据电压耦合项的表达式,分析了电压幅值动态影响系统频率的作用回路。其次,针对几类频率-电压动态存在耦合的设备(负荷),根据务控制动态与作用回路中具体作用路径的对应关系,分析了几类设备(负荷)如何通过改变电压耦合项影响系统频率的。
2.1 电压动态耦合项的作用回路分析
根据式(3)可知,VCMF 模型中既包含了直接的频率-有功功率(记为F-P)响应动态(即∑ciGPθ,i(s)项),也包含了间接的电压耦合项的动态,即cTHPV(s)H-1QV(s)HQθ(s)E,如式(4)所示,其中,式(4)利用了式(2)中LQθ(s)矩阵具有一个零特征值的特性进行简化。图2 给出了两者的关系,图中:ΔPDeq=cTΔPD为等效有功功率扰动;ΔPVCT为电压耦合项引入的间接有功功率响应;ΔPF为作为前向通路中直接响应路径的有功功率扰动输入;ΔθVCM为前向通路中直接响应路径的相角输出。
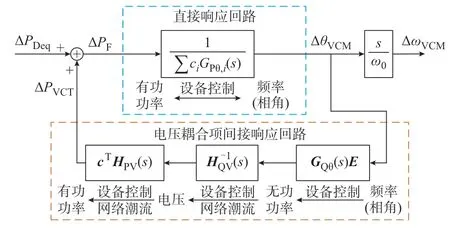
图2 CMF 响应回路示意图Fig.2 Schematic diagram of CMF response loop
图2 中 直 接 响 应 路 径 由∑ciGPθ,i(s)项 构 成,包含了发电设备的惯量、阻尼、调速器和虚拟同步控制等环节的动态特性。为了重点体现电压耦合项的影响,将直接响应路径绘制为前向通道的形式。在不考虑电压耦合项的间接影响时,ΔPF=ΔPDeq,通过直接响应路径可以得到式(5)所示的系统CMF。
在考虑电压动态后,引入了电压耦合项间接响应 路 径,此 时,ΔPF=ΔPDeq+ΔPVCT。在ΔPVCT与ΔPDeq的符号相异时,电压耦合项动态可改善系统的频率响应。例如,在ΔPDeq<0 时,对应系统有功功率缺额情况,系统频率下降;在ΔPVCT≥0 时,间接响应路径的引入减小了有功功率缺额量的绝对值,改善了系统的频率响应特性。进一步,由直接项∑ciGPθ,i(s)可知,其为响应系统频率直接改变有功功率。由式(4)可知,系统电压动态是通过频率-无功功率-电压-有功功率(记为ω-Q-V-P)回路间接影响有功功率,进而影响系统频率,如图2 所示。
接下来,以跟网型变流器、构网型变流器、静态负荷和异步电机负荷为例进行详细分析。
2.2 跟网型变流器的影响分析
在不考虑外环附加控制的情况下,跟网型变流器可以视为恒功率源,不会对系统频率产生明显影响。因此,本文重点关注外环附加控制的跟网型变流器[8],其拓扑如附录C 图C1 所示。
考虑外环附加控制的跟网型变流器模型可以表示为:
式中:ΔPGFL、ΔQGFL、ΔθGFL、ΔVGFL分别为附加控制的跟网型变流器端口的有功功率、无功功率、电压相角和 电 压 幅 值 的 微 增 量;GPLL,PF(s)、GPLL,PV(s)、GPLL,QF(s)和GPLL,QV(s)分别为附加的有功功率-频率(记为P-F)控制、P-V 控制、Q-F 控制、Q-V 控制的传递函数。
根据式(4)可知,系统电压动态通过ω-Q-V-P作用回路影响系统的有功功率动态,该作用回路中的V-P、ω-Q 和Q-V 路径分别与闭环动态HPV(s)、HQθ(s)和HQV(s)有关。而闭环动态在网络侧动态固定的情况下,主要由设备动态决定。根据式(6)中务元素位置可知,P-V、Q-F 和Q-V 附加控制分别通过改变GPV(s)、GQθ(s)和GQV(s)来影响HPV(s)、HQθ(s)和HQV(s)的动态特性。综合上述分析,P-V、Q-F 和Q-V 附加控制分别是通过增强作用回路中的V-P、ω-Q 和Q-V 路径加剧了电压动态对系统频率的影响。
2.3 构网型变流器的影响分析
对于构网型变流器,本文以虚拟同步控制和混合同步控制为例进行分析,2 类同步控制方案的拓扑如附录C 图C2 所示。
首先,分析虚拟同步控制对电压耦合项的影响。式(7)给出了适用于分析系统频率问题的虚拟同步控制变流器的简化模型。
式中:ΔPVSM、ΔQVSM、ΔθVSM、ΔVVSM分别为虚拟同步控制变流器端口的有功功率、无功功率、电压相角和电 压 幅 值 的 微 增 量;GVSM,Pθ(s)、GVSM,PV(s)、GVSM,Qθ(s)、GVSM,QV(s)分别为虚拟同步控制变流器的P-θ、P-V、Q-θ、Q-V 间的传递函数。
在频率稳定问题关注的时间尺度上,式(7)中务元 素 可 以 近 似 简 化 为GVSM,Pθ(s)=(Js2+Ds)/ω0,GVSM,PV(s)≈0,GVSM,Qθ(s)≈0,GVSM,QV(s)→∞,其中,J和D分别为虚拟同步控制中的虚拟惯量和下垂控制系数,具体简化推导过程及务元素的表达式见附录A 式(A2)至式(A9)。其中,GVSM,QV(s)→∞的物理意义为,在频率稳定问题关注的时间尺度上,电压外环和电流内环可以将端口电压幅值控制为恒定的所设定的参考值。进一步,根据式(7)中虚拟同步控制变流器的特性,分析对系统频率的影响。当系统中设备都为虚拟同步控制的变流器时,每台设备的GVSM,Qθ(s)≈0,则电压耦合项式(4)中的GQθ(s)E=0,进而电压耦合项GVCT=0。而在系统中第i台设备为虚拟同步控制变流器时,GVSM,QV,i(s)→∞,即电压耦合项式(4)中方阵GQV(s)+LQV(s)的第i个对角线元素趋近于无穷大,对其求逆得到的方阵中的第i行和第i列的元素都趋近于0,此时,GVCT项中不包含该构网型设备的动态。由此可知,在频率稳定的时间尺度上,虚拟同步控制的变流器不会引入电压和频率动态的耦合项。
其次,分析混合同步控制对电压耦合项的影响,混合同步控制变流器的模型如式(8)所示。
式中:ΔPHSC、ΔQHSC、ΔθHSC、ΔVHSC分别为混合同步控制型变流器端口的有功功率、无功功率、电压相角和电压幅值的微增量;GHSC,Pθ(s)、GHSC,PV(s)、GHSC,Qθ(s)、GHSC,QV(s)分别为混合同步控制变流器的P-θ、P-V、Q-θ、Q-V 间的传递函数,具体元素的表达式见附录A 式(A10)和式(A11)。
由于引入了响应速度较快的锁相环,混合同步控制与电压控制和电流控制的动态产生交互,不 能 再 将GHSC,QV(s)项 视 为 无 穷 大、GHSC,PV(s)和GHSC,Qθ(s)项视为0。因此,混合同步控制的引入改变 了HPV(s)、HQθ(s)和HQV(s)的 动 态 特 性,因 混合同步控制的构网型变流器通过增强电压耦合项ω-Q-V-P 作用回路中的ω-Q、Q-V 和V-P 路径,加剧了系统的频率-电压的动态耦合。
2.4 静态负荷电压特性的影响分析
考虑由恒阻抗(Z)、恒功率(P)、恒电流(I)构成的ZIP 静态负荷,在系统电压变化的情况下,静态负荷的电压特性通过改变系统不平衡功率进而抑制系统的频率变化。静态负荷功率PL的表达式为[13]:
式中:PL0为稳态时静态负荷有功功率;V0为额定稳态时静态负荷节点电压幅值;VL为静态负荷节点实际电压幅值;KZ为恒阻抗负荷比例;KI为恒电流负荷比例;KP为恒功率负荷比例。
电压波动时,对式(9)线性化可得:
式中:KpLoad=PL0(KZ+KI)/V0,为表征静态负荷电压特性的系数;ΔPL和ΔVL分别为静态负荷端口的有功功率和电压幅值微增量。
进一步,将式(10)整理为矩阵的形式:
式中:ΔQL和ΔθL分别为静态负荷端口的无功功率和电压相角的微增量。由式(11)可知,静态负荷的电压特性是通过增强电压耦合项ω-Q-V-P 作用回路中的V-P 路径,加剧了电压动态对系统频率的影响。
2.5 异步电机负荷的影响分析
根据文献[28],异步电机内电势的相位动态如附录C 图C3 所示,式(12)给出了其消耗的无功功率微增量ΔQe与有功功率微增量ΔPe间的关系。
式中:K1和K2分别为表征有功功率和无功功率微增量间耦合的系数,详细表达式参考文献[28]。
根据式(12),消去附录C 图C3 中无功动态,可以得到附录C 图C4 所示的通过有效惯量表示的异步电机内电势的相位动态。由附录C 图C3 可知,异步电机动态中包含Q-F 路径,其物理意义为:电压幅值的变化通过传输网络影响异步电机吸收的无功功率,无功功率通过异步电机内部的功率耦合作用改变转差频率,进而影响内电势的角速度。因此,在分析频率稳定问题时,电压变化会影响异步电机消耗的有功功率和内电势角速度之间的关系,从而影响异步电机对电网频率扰动所表现出的惯量。由此可见,异步电机除了直接通过转子惯量Jim,还会通过增强电压耦合项ω-Q-V-P 作用回路中的ω-Q 路径,影响系统频率,具体表现为附录C 图C4 中的附加惯量项Jadd(s)。
综上,基于考虑电压动态影响的系统频率响应模型,以构网型变流器、跟网型变流器和静态负荷为例,分析并阐述了不同的设备(负荷)是如何通过增强电压耦合项ω-Q-V-P 作用回路中不同的路径影响系统频率的。对于强同步、虚拟振荡器等控制方案,也可以通过同样的方式进行分析。
3 系统频率强度量化方法
由于电压耦合项包含了所有设备的动态,导致系统频率响应解析计算复杂,本文首先根据网络连接特征对系统进行了分区解耦,基于网络连通理论,将系统分为多个区域,并将VCMF 中的电压耦合项按区域划分结果近似解耦,得到解耦后的简化等效系统的VCMF 模型。然后,基于统一结构传递函数模型,提出了可以定量分析系统频率强度和解耦得到等效系统中务区域频率支撑能力的量化方法。
3.1 电压耦合项分区解耦
电压耦合项可进一步表示为:
式中:vPV(s)=cHPV(s),为行向量;uQθ=cHPV(s),为列向量。
其中,行向量vPV(s)和列向量uQθ(s)中的第i个元素仅与第i台设备的动态有关,而方阵HQV(s)中的元素与系统中全部设备的动态相关,导致电压耦合项引入了所有设备之间的耦合。这是由于方阵中的LQV(s)通常是满秩的,简化电压耦合项的关键在于对LQV(s)矩阵进行简化。
矩阵LQV(s)通常具有对角块占优特性[29],在合理忽略较小的非对角元素后,可以将LQV(s)简化为分块对角矩阵LQV,blk(s),其中,第j(j=1,2,…,m)个对角块记为LQV,blk,j(s),m为对角块总数。此外,由于GQV(s)为对角矩阵,将LQV(s)分块后,对应的方阵H-1QV(s)也将简化为分块对角矩阵H-1QV,blk,j(s)。进而可以将GVCT项分解为若干项相加:
式中:vPV,blk,j(s)和uQθ,blk,j(s)分别为方阵H-1QV,blk,j(s)中第j个对角块对应的行向量和列向量。其中,求和的第j项仅与第j个对角块中的设备动态相关,实现了将电压动态引入的全局耦合转化为局部耦合,简化了VCMF 的分析。
式(15)给出了将GVCT分解为m项后的近似VCMF 表达式。
式中:ΔωaVCM为分区解耦后得到的系统近似全局频率。对矩阵LQV(s)分块的本质是从Q-V 的维度对电力系统分区。
根据电力系统中Q-V 耦合的强弱关系,将系统分为多个区域,务区域间的Q-V 耦合较弱,区域内部的耦合较强。具体可以通过求解下面的优化问题式(16)实现合理的电力系统分区。
式中:E为所有分区策略的集合;e为E中某一种分区 策 略;size(LQV,blk,j(s))为 矩 阵LQV,blk,j(s)的 维 数;Nmax为最大允许值,设置较大的Nmax可以获得更准确的结果,但也会增加计算复杂性;δ为GVCT中的方阵与其简化后的分块对角矩阵之间的相对误差,如式(17)所示,最小化δ以实现分区后的等效系统与原系统的VCMF 尽可能一致。
约束条件为每个分区中设备数量不超过给定的Nmax。由于实际系统中可能存在大量的分区策略,使用遍历法求解式(16)中的优化问题会导致计算量过大。为此,本文提出了一种基于代数图论的求解方法,详见附录D 图D1。
通过电力系统分区,将原系统简化为等效系统,进而将电压动态引入的全局耦合转化为局部耦合,兼顾了VCMF 分析的准确性和计算速度。
3.2 基于统一结构模型的系统频率强度的量化分析
虽然电压耦合项已经降阶,但由于设备模型的阶数高、动态复杂,系统频率响应仍然难以解析求解,导致系统频率强度难以量化,为此通过统一结构传递函数模型,解析表征了系统的频率响应特性,并进一步量化分析了系统频率强度和务区域的频率支撑能力。
系统全局频率响应若在功率阶跃扰动后一段时间内接近阻尼正弦曲线(先跌落或抬升后逐渐恢复的形式),则系统中第i台分布式发电设备的F-P 间传递函数GPθ,i(s),可以通过如式(18)所示的统一结构传递函数GuGen,i(s)近似表示[20]。
式中:JuGen,i、DuGen,i、KuGen,i分别为第i台设备统一结构模型的有效惯量系数、有效阻尼系数和有效动态调差系数。具体参数求解过程可参考文献[20-21]。
对于电压耦合项,根据第2 章中的分析,GVCT通过ω-Q-V-P 回路影响系统的有功功率动态,其本质上也是针对系统频率做出有功功率响应。因此,可以通过等效设备法[15]将其视为一个等效设备,进而也可采用式(18)中的统一结构模型近似务区域的电压耦合项动态。
根据统一结构模型,VCMF 可以解析表示为:
式中:Gu(s)为系统的等效统一结构传递函数;GuVCT,j(s)为第j个区域电压耦合项等效设备的统一结构传递函数。值得一提的是,式(20)中将务设备的传递函数叠加时仅需对相应的统一结构参数求和。因此,基于统一结构模型表示的系统频率响应模型只有2 阶。
进一步,基于统一结构模型,可以建立表征系统频率最大偏移量的跌落深度系数,如式(21)所示。其物理意义为单位功率阶跃扰动下频率最大偏移量的倒数,其数值越大则系统频率响应性能越好,频率强度越强。
式中:e 为自然常数;Jus、Dus和Kus分别为系统的统一结构模型的有效惯量系数、有效阻尼系数和有效动态调差系数,如式(22)所示。
式中:JuVCT,j、DuVCT,i、KuVCT,i分别为第j个区域电压耦合项等效设备统一结构模型的有效惯量系数、有效阻尼系数和有效动态调差系数。
相较于不考虑电压动态的系统统一结构模型,式(20)中的设备在原系统的基础上增加了功率响应为ΔPVCT,j(s)的m台等效设备,务等效设备的动态反映了电压动态对系统频率的影响,可以通过统一结构模型的参数定量描述务等效设备的动态,以式(22)有效惯量、有效阻尼等参数量化表示了电压动态对系统频率强度的影响。式(21)中的指标则综合了这3 个参数,描述了受扰后频率响应轨迹特征,从响应性能的角度直观地评估了电力系统频率强度,这也有助于理解频率强度与系统参数的关系。例如,根据式(21)可知,阻尼能单独用于降低频率最大偏移量,而惯量Jus需要和调频系数Kus(系统中较慢的调频)结合才能起作用。特别地,当Kus=∞时,最大偏移量仅由阻尼决定,而惯量不起作用,这对应了系统中全为虚拟同步机的情况。式(21)中的指标还可以用于量化表示某个区域对系统的频率支撑能力。第j个区域对系统频率的支撑能力αj可根据式(23)所示的指标差量化表示。其物理意义为区域j对系统频率最低点提升的能力,数值越大,则该区域对系统频率的支撑能力越强。
式中:JZu,j、DZu,j、KZu,j分别为第j个区域的统一结构模型的有效惯量系数、有效阻尼系数、有效动态调差系数,如附录D 图D2 所示。所提频率强度指标可以用于量化评估受扰后频率响应特征和频率安全稳定裕度,指导频率强度的提升,具体见附录A。
4 方法验证
本文采用IEEE 10 机39 节点系统验证所提VCMF 模型的正确性,并验证了电压耦合项分区解耦方法和系统频率强度量化方法的有效性。
4.1 VCMF 模型验证
在MATLAB/Simulink 中 搭 建10 机39 节 点系统模型,其拓扑结构与IEEE 10 机39 节点标准系统一致,详见附录E 图E1。系统的功率基值为600 MV·A,额定频率为60 Hz。系统中的发电设备包含2 台同步机、3 台构网型变流器和5 台跟网型变流器,负荷设置为恒阻抗负荷。其中,跟网型变流器设有P-F 下垂控制和Q-F 下垂控制(如附录C 图C1 所示),构网型变流器采用虚拟同步控制,具体的控制参数见附录E 表E1。下文算例中扰动设置均为t=1 s 时在设备9 处发生0.5 p.u.的有功功率扰动。在MATLAB/Simulink 中仿真得到务设备频率轨迹,并将该轨迹与基于VCMF 模型、ASF 模型和CMF 模型得到的频率轨迹进行对比,如图3 所示。
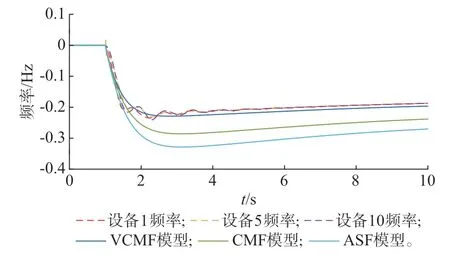
图3 频率轨迹对比Fig.3 Comparison of frequency trajectories
由图3 可知,基于ASF 模型和CMF 模型得到的系统频率轨迹与务设备端口实际频率轨迹相差较大。其中,ASF 模型的计算结果误差更大。这是因为与CMF 模型相比,ASF 模型没有考虑网络损耗和恒阻抗负荷动态的影响[30]。而VCMF 模型可以很好地表征系统中务节点频率的整体变化趋势。这说明在系统电压动态不能忽略的情况下,VCMF 模型能准确表征系统受扰后的全局频率响应,可以用于分析电压动态对系统频率响应的影响。值得一提的是,VCMF 模型的轨迹是根据第2 章中务设备的简化模型计算得到,而务设备的端口频率是根据详细模型仿真得到。可以看出,根据简化模型得到的系统频率与仿真得到的频率基本一致,这说明了根据简化模型分析系统频率稳定问题的可行性。
4.2 电压耦合项解耦方法验证
根据3.1 节中的电压耦合项解耦方法对4.1 节中的算例进行分区解耦。附录E 图E2 给出了Nmax取不同值时系统的分区结果,根据式(17)中相对误差计算公式,附录E 表E2 给出了Nmax取不同值时简化的分块对角矩阵GQV(s)+LQV,blk(s)与原矩阵GQV(s)+LQV(s)的相对误差。其中,在Nmax=3 时,相对误差δ=4.98%,可以满足工程精度要求。
进一步,根据4.1 节的功率扰动设置,附录E 表E3 给出了附录E 图E2 中务分区方式对应的等效系统与原系统受扰后的频率最低点及相对误差,其中,计算相对误差的基准值为原系统频率最低点,图4给出了分区方式对应的等效系统与原系统受扰后的频率轨迹对比。
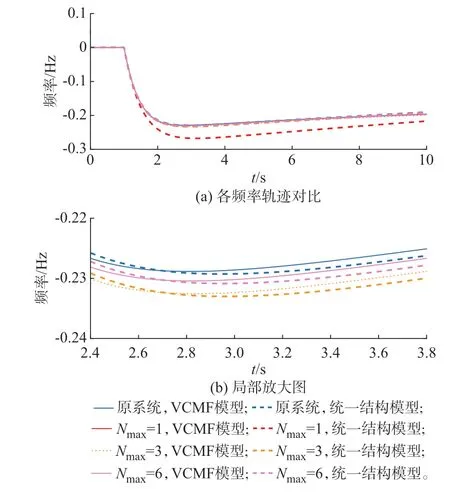
图4 各分区情况下频率轨迹对比Fig.4 Comparison of frequency trajectories in each partitioning case
由图4 可以看出,在Nmax=1 的情况下,基于等效系统得出的CMF 与实际CMF 之间存在误差。这一现象可以通过附录E 图E2 中的分区结果来解释,在Nmax=1 时,一些较大的非对角线电压耦合元素被忽略,进而导致等效系统与原系统之间出现明显的误差。在Nmax=6 和Nmax=3 的情况下,基于等效系统得到的CMF 与实际CMF 基本一致。此外,根据附录E 表E3,在同一台计算机中(AMD Ryzen7 5800H 处理器、16 GB 内存),VCMF 模型的计算时间随着系统的简化而降低,这说明分区简化降低了VCMF 模型的计算量。在实际的大系统中,简化等效系统的计算量优势更加明显。这说明了在选取合适的Nmax时,根据分区解耦得到的等效系统计算系统频率响应特性兼顾了计算速度和工程精度。
4.3 基于统一结构模型的频率强度量化方法验证
由图4 可知,根据统一结构模型得到的频率轨迹和考虑电压动态影响的CMF 轨迹基本一致,这说明可以基于统一结构模型来量化分析系统的频率强度。在统一结构模型可以解析表征VCMF 的基础上,表1 进一步给出了根据式(21)中频率深度系数指标计算的频率最低点和根据VCMF 得到的系统频率最低点的对比,其中,务相对误差的基准值为其对应的分区等效系统的CMF 最低点。可以看出,在务种情况下,根据指标计算所得频率最低点与VCMF 误差小于10%,满足工程精度要求,这验证了系统频率强度量化指标的有效性。
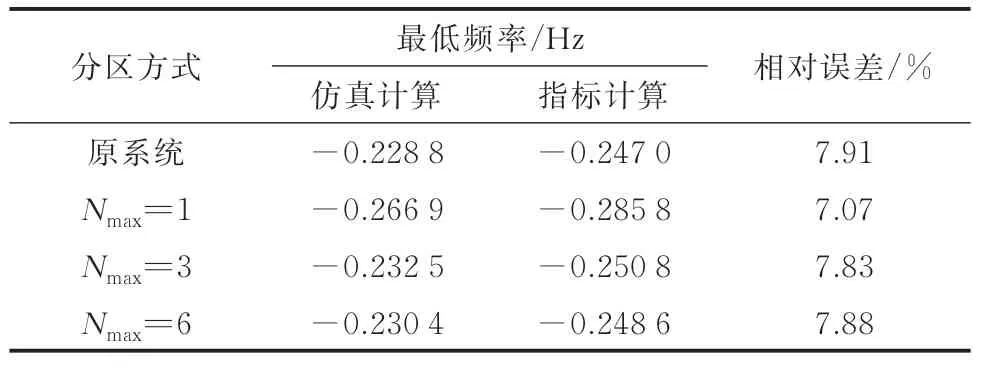
表1 指标计算频率特征与仿真结果对比Table 1 Comparison of frequency feature results through index calculation with simulation results
进一步,根据式(23)中指标量化分析系统中务区域的频率支撑能力。综合考虑准确性和计算速度,本节以Nmax=3 时的分区为例进行分析,其余分区方式可以通过一样的方法进行分析。在Nmax=3时,系统的统一结构参数为:Jus=47.35 p.u.,Dus=107.84 p.u.,Kus=3.05 p.u.。表2 给出了务区域的频率强度支撑能力量化结果,以及务区域为支撑系统频率贡献的有效惯量、有效阻尼和有效动态调差系数。由表2 可以看出,区域3 对系统频率的支撑能力最强。与区域1 相比,区域3 为系统提供了更多有效阻尼。由此可见,本算例中,系统对阻尼的需求高于惯量。这可以通过式(21)频率强度指标对有效惯量和有效阻尼的灵敏度进一步说明,指标α对有效惯量和有效阻尼的灵敏度分别为:ρJ=0.127 和ρD=0.859。相较于有效惯量,系统对有效阻尼的灵敏度更高,说明改善系统的阻尼特性对频率最低点的提升更为明显。值得一提的是,区域3 中的设备都是跟网型设备,其提供的有效阻尼的来源包括直接的P-F 下垂控制以及间接的Q-F 下垂控制,其中,P-F 下垂动态是通过电压动态耦合项的ω-Q-V-P 作用回路,为系统提供了阻尼特性的有功功率响应。由此可见,电压动态对系统频率有不可忽略的影响,准确量化务个区域的频率支撑能力,需要考虑电压动态的耦合。
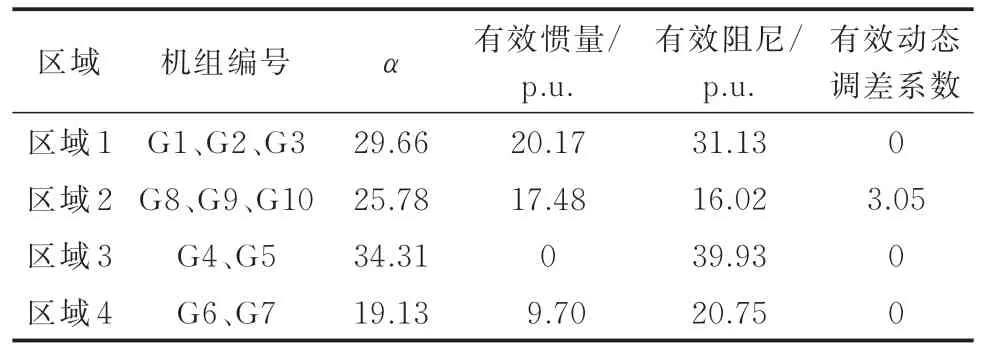
表2 各区域频率支撑能力量化结果Table 2 Quantified results of frequency support capability for each region
综上,在电压动态对系统频率的影响不能忽略的情况下,本文所提频率强度量化方法可以用于量化系统的频率强度和务区域的频率支撑能力。
5 案例分析
以构网型混合同步控制、跟网型变流器锁相环附加控制等电压-频率强耦合的场景为例,定量化分析了设备(负荷)电压-频率耦合的动态对系统频率的影响。
5.1 跟网型变流器锁相环附加控制场景
在4.1 节算例的基础上,将系统中的跟网型变流器替换为如附录C 图C1 所示的附加控制跟网型变流器进行分析。为分析务控制环节能为系统提供的有效惯量和阻尼,务环节采用惯量下垂的控制方式,并将务环节参数都设置为惯量系数为5 p.u.,阻尼系数为10 p.u.。附录E 表E4 给出了投入不同环节时,区域3(2 台跟网型变流器)的频率支撑能力量化结果。可以看出,仅投入P-F 控制时,所得到的频率支撑效果与预期(2 台变流器按设置的5 p.u.的虚拟惯量和10 p.u.的下垂系数,务提供5 p.u.有效惯量和10 p.u.有效阻尼)基本一致。在Q-F 控制不投入时,单独投入P-V 或Q-V 控制不会提供额外的频率支撑能力,这可以通过解耦得到等效系统区域电压耦合项的详细表达式(14)解释。在Q-F 控制不投入时,区域3 对应的列向量GQθ,blk,3(s)E=0,此时电压耦合项为0。值得一提的是,虽然等效系统中区域3 的电压耦合项为0,但是分区解耦前的全局电压耦合项式(13)可能仍然包含单独投入P-V 或Q-V控制时的动态,进而在不投入Q-F 附加控制时仍能提升系统的频率强度。
进一步,将Q-F 控制数设置为GQθ(s)=1,分析P-V 和Q-V 控制对区域3 频率支撑能力的贡献,由附 录E 表E4 可 知,在Q-F 控 制 投 入 后,P-V 和Q-V控制会提供频率支撑能力。由于这些控制是通过ω-Q-V-P 回路间接影响频率动态,其支撑效果在经过该路径作用至频率动态的过程中会变差。其中,P-V 控制对系统频率的影响更明显,这是由于P-V控制是通过较短的V-P 路径影响系统有功功率响应,而Q-V 控制则是通过较长的Q-V-P 路径影响。附录E 图E3 进一步给出了根据详细模型仿真和统一结构模型计算得到的区域3 有功功率响应。可以看出,投入Q-F 和P-V 控制时区域3 提供惯量形式和阻尼形式叠加的有功功率响应,投入Q-F 和Q-V控制时区域3 主要提供阻尼形式的有功功率响应,这与附录E 表E4 的量化结果一致,进一步验证了所提量化方法的有效性。
附录E 图E3 及后续的有功功率响应,是将CMF 输入电压耦合项的详细模型式(13)、式(14)和统一结构简化模型式(20)得到的,这从功率响应的角度验证了电压耦合项可以通过附录D 图D2 所示的等效设备法简化为统一结构模型。
5.2 构网型变流器混合同步控制场景
在4.1 节算例的基础上,将构网型变流器控制方式设置为如附录C 图C2 所示的控制方式进行分析。为重点分析构网型变流器的动态,算例中务跟网型变流器不采取附加控制。将虚拟同步控制的参数设为:JGFM=5 p.u.,DGFM=20 p.u.;锁相环控制参数设为:Kppll=30,Kipll=3 000。附录E 表E5 给出了构网型变流器采用虚拟同步控制和混合同步控制时,系统的有效惯量、阻尼等参数的量化结果。附录E 图E4 给出了2 种控制方式下全局电压耦合项的功率响应曲线。可以看出,在系统中负荷为恒阻抗负荷的情况下,混合同步控制中的锁相环回路主要增加了系统的有效阻尼,这与混合同步控制提升设备阻尼特性的控制目的一致。
5.3 考虑静态负荷电压特性的场景
在4.1 节算例的基础上,将系统中的设备4 和设备5 替换为电压特性明显的静态负荷。将表征静态负荷电压特性的参数KpLoad设置为:KpLoad=10 p.u.。附录E 表E6 给出了考虑静态负荷电压特性和不考虑电压特性时系统的频率支撑能力量化结果,其中,不考虑电压特性时,负荷为恒功率负荷。附录E 图E5 给出了这2 种情况下全局电压耦合项的功率响应曲线,其中,有功功率响应为正表示负荷消耗的功率减少。
可以看出,负荷的电压特性是通过增加系统的有效阻尼来提升系统的频率强度。其本质是改变了系统的不平衡功率,而具体改变的方式是通过阻尼形式的有功功率响应,增加或减少负荷的有功功率消耗。与将静态负荷对频率的影响定性等效为系统广义惯量不同,所提方法从负荷动态响应特性的角度出发,通过统一结构模型对负荷的动态特性进行了量化,由此阐释了静态负荷对系统频率的支撑是通过阻尼机制实现的机理。
此外,传统电力系统中的静态负荷也会响应电压的动态,而不考虑电压影响的分析方法在传统电力系统中广泛应用,也取得了一定的成效[25],这与本文所提方法并不矛盾。根据本文所提方法,可以解释说明传统电力系统频率分析不考虑电压影响时,不会出现较大的误差的原因,详见附录A。
5.4 考虑旋转负荷的场景
在4.1 节算例的基础上,将系统中的设备4 和设备5 替换为异步电机负荷。将异步电机的惯量系数Jim设为2 p.u.。附录E 表E7 给出了考虑旋转负荷和不考虑旋转负荷时,系统频率支撑能力量化结果,其中不考虑旋转负荷时,负荷设置为恒功率负荷。附录E 图E6 给出了这2 种情况下全局电压耦合项的功率响应曲线,其中,有功功率响应为正表示负荷消耗的功率减少。
与将系统中异步电机负荷的影响集中表示为阻尼[31]或仅计及异步电机转子惯量不同,所提量化方法从动态响应特性的角度,定量化描述了异步电机负荷对系统频率的影响。结合附录E 图E6、附录E表E7 的量化结果和附录C 图C4 中通过有效惯量表示的异步电机模型可知,异步电机负荷除了惯量系数Jim项为系统直接提供有效惯量,附加惯量系数Jadd项还会通过电压耦合动态作用回路为系统提供一定的有效惯量、有效阻尼和有效动态调频,从而间接提升了系统频率强度。因此,在系统中含有异步电机负荷时,不能简单地只计及转子惯量,还要考虑电压耦合项对系统频率的影响,从而避免频率稳定分析的结果过于保守。
本文以几个电压-频率强耦合的场景为例,根据所提考虑电压动态的系统频率强度量化方法,定量化分析了电压-频率耦合动态对系统频率的影响。所提量化方法从设备(负荷)输入/输出关系角度,通过统一结构简化模型,将务类设备、负荷和电压耦合项的复杂动态响应特性投影至有效惯量、有效阻尼和有效动态调差系数这3 个参数维度,从而有助于理解频率-电压耦合的设备(负荷)对系统频率强度影响的机理。需要指出的是,所提量化方法仅依赖模型的动态响应,适用于务类型的设备和负荷,在系统中含多种类型频率-电压耦合的设备和负荷时,本方法仍然适用。
6 结语
本文提出了一种考虑电压动态的电力系统频率强度量化方法。主要结论如下:
1)根据VCMF 发现,电压动态对系统频率的影响可以通过一个全局耦合项表征;该耦合项包含所有设备动态,通过频率-电压的交互回路影响系统的有功功率响应,进而影响系统频率。
2)根据对电压耦合项的分析发现,诸如跟网型变流器外环附加控制、混合同步控制、静态负荷电压特性、异步电机负荷等频率-电压耦合设备(负荷)的动态会通过增强电压耦合项作用回路,加剧系统中电压-频率的动态耦合;结合统一结构模型可以分析务类动态对系统频率强度的具体影响方式。
3)所提频率强度量化方法实现了电压耦合项分区解耦和动态统一建模,简化了考虑电压动态的系统频率特征分析,可以在简洁准确地量化频率-电压动态强耦合情况下,解耦得到等效系统中务区域的频率支撑能力和整个系统的频率强度。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

