计及典型控制的风电场调频能力量化评估及影响因素分析
阮益闽,宗启航,姚 伟,周泓宇,张鑫灏,文劲宇
(强电磁工程与新技术国家重点实验室(华中科技大学),湖北省武汉市 430074)
0 引言
在“双碳”战略目标的指引下,以风电为代表的新能源在中国电力系统中的占比迅速提升[1-3]。为了进一步保障系统的频率安全,风电场等新能源场站需要具备一定的调频能力[4-6]。而在进行频率支撑时,有必要对风电场的调频能力进行量化评估,从而合理地分配务发电单位的调节功率,以避免因调频能力不足而造成频率持续跌落,或是能力过剩而造成资源的浪费[7-8]。然而,与同步机不同,风电系统的调频能力受风力资源和自身运行状态等条件的影响,难以准确量化估计[9-10]。
为使风电场具备一定的调频能力,现有调频方案主要分为两种类型:基于转子动能控制[11-13]和基于备用功率控制[14-16]。前者利用转子动能的快速释放在频率响应的初期进行频率支撑,响应速度快但支撑时间较短;后者考虑减载运行,在频率响应时释放备用功率进行频率支撑,支撑时间长但经济性较差。文献[17]将附加下垂控制和超速减载控制相结合,同时体现了两类调频方法的优势,本文将以该方案为例进行评估分析。
对于调频能力量化评估的研究,文献[18]基于自定义的转子转速限制因子和变流器容量限制因子,计算了风机调频能力系数,并基于该指标合理分配调节功率,实现了风电场务风机单元的虚拟惯量协同控制。文献[19]建立了风机的稳态小干扰模型,并基于该模型计算了风电场稳态时等效下垂系数表达式。文献[20]计算了风电系统接入电网后等效下垂系数和惯性系数的理论真值,并结合系统频率最低点和最大频率偏差的设计要求,评估了风电场综合惯性调频方案的控制系数范围。文献[21]利用Koopman 算子对历史调频数据进行拟合,评估了风电场在转速约束下的极限下垂系数。以上研究仅评估了间接衡量调频能力的相关系数,并没有具体地计算有功出力值,只适用于场站内部的调频功率分配。
为评估有功出力具体值,部分研究对评估指标做出了改进。文献[6]将转子可用动能定义为调频能力指标,并基于该指标设计自适应下垂系数,使得风机调频能力最大限度发挥,但未考虑更多的约束限制和备用功率的支撑作用。文献[22]将风电场简化模型中的非线性部分转化为线性结构,通过混合整数线性规划求解风电场在务安全运行约束下暂态增发功率的边界值,但该研究忽略了风电有功资源的复杂性,将不同能量形式的功率同时考虑,评估结果较为粗糙。文献[23]考虑了风电场风速的时空分布特性,将其有功功率资源分为转子动能和备用功率两种形式,更加合理地评估了支撑能力,但未考虑频率响应时风机的务安全运行约束对支撑能力的限制,评估结果较为理想。
针对现有文献的不足,本文首先建立了基于减载和下垂控制的风电调频结构。其次,针对风电场频率支撑特性定义了量化调频能力的多时间尺度、多能量形式、多评估层次指标。进一步,分析了转速、载荷和容量约束对备用能量和转子动能释放的影响机制,揭示了风电场运行参数对调频能力影响的定性结论。接着,建立风电场调频能力优化模型,采用非线性规划算法准确求解所定义量化指标。最后,对含单机聚合风电场的四机两区域系统进行算例分析,进一步验证了所提方法的准确性以及影响因素分析结论的正确性。
1 基于减载和下垂控制的风电调频模型
下垂控制和超速减载控制作为最常见的两种风电场频率支撑策略,具有一定的代表性意义,风电场在两种方法的共同作用下,调频能力将显著提升[17]。本文将基于超速减载和下垂控制相结合的调频策略,对风电场的调频能力进行分析与评估。本文主要考虑惯性尺度和一次尺度下的频率支撑过程。因此,可忽略部分电磁时间尺度的结构,简化后的双馈风机有功支撑模型如附录A 图A1 所示。
风机捕获的机械功率Pm可以表示为:
式中:λ=ωrR/Vw为叶尖速比,其中Vw为风机所处位置的风速,ωr为转子转速,R为风轮半径;β为桨距角;ρ为空气密度;CP为风能利用系数;λi为计算中间变量。风机的捕获功率主要与风速、转速和桨距角大小有关。
将CP在稳态工作点进行泰勒展开,忽略高阶项后写成二阶多项式的形式:
式 中:c2=-0.010 1,c1=-0.004 2β+0.207 7,c0=0.024 3β-0.614 0,都是关于β的线性表达式,且在桨距角变化后立即更新。
因此,式(1)可重写为:
风机功率输出最大的运行点被称为最大功率点跟 踪(maximum power point tracking,MPPT)点。随着风速的变化,最大功率输出点对应的转速随之变化,二者组成MPPT 工作曲线。在二次型曲线顶点处取得功率极值Pmppt:
式中:kopt为MPPT 曲线拟合系数。
当风机采用超速减载策略,其工作运行点将固定在提前设定的减载曲线上。此时初始减载输出功率Pm0和MPPT 点输出功率Pmppt的关系为:
式中:kdel为风机的减载系数,一般按照百分比的形式设置。
风电场检测到频率扰动Δf后,按照场站预设的下垂系数kdr附加到定子功率参考指令ΔPsref:
忽略变流器的电磁响应环节,将附加功率指令后得到的总参考指令Psref作为实际功率输出,而定子功率Ps与电磁转矩Te的标幺值相等,即
在频率支撑过程中,风机转子受到的电磁转矩Te和机械转矩Tm不相等,由风机转子的动力学方程得到:
式中:J为风机的机械转动惯量。
在中低风速下,采用超速减载的功率备用方案。风机初始时刻工作于减载运行点,当系统发生功率扰动后,受下垂控制作用,电磁转矩响应变化,使转子受到不平衡转矩从而减速,风机工作运行点由减载点向MPPT 点移动,从而释放备用功率和转子动能以进行频率支撑。
值得注意的是,采用之前工作中提出的转速恢复策略能最大化减小二次频率跌落[6]。因此,本文并未考虑转速恢复对调频能力的影响,即认为在风电场频率支撑过程结束后再采用最优恢复策略使风机恢复到原有运行状态。
2 风电调频能力量化指标定义与分析
2.1 调频能力的最大潜力
当电力系统发生有功功率扰动时,风电场将会调整其有功功率以进行频率支撑。风电系统响应的有功功率按照能量的来源可分为2 个分量:储存于转子旋转动能提供的转子动能功率分量和储存于风能中的备用功率分量,如图1(a)所示。图中:kPFR为备用功率分量极限响应速度;ΔPm为备用功率稳态释放量;P0为初始功率;t0为调频初始时刻;tm为转子动能完全释放的时刻;tset为调频稳态时刻。特别的,转子动能功率分量主要作用于扰动发生后短时间内的惯性时间尺度,起到短时支撑作用;而备用功率分量则主要作用于一次时间尺度,起到长时间的支撑作用。因此,有必要从多时间尺度、多能量形式的角度量化评估风电系统的调频能力。
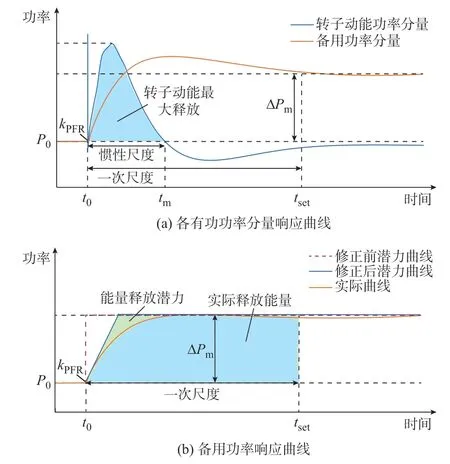
图1 风电场有功功率响应曲线Fig.1 Active power response curves of wind farm
2.1.1 惯性尺度下转子可用动能
存储于转子中的转子动能在频率支撑过程的初期起到十分重要的作用。因此,较多调频方案利用了该部分能量对系统进行惯性支撑和初期的一次调频[6,13]。然而,该部分有功功率资源是有限的,风机的转子可释放动能主要受到最低转速的限制。以向上调频为例,当转速跌落至安全转速范围以下时,该风机将退出调频,甚至失步退网,从而造成频率二次跌落等事故[24]。
转子动能的释放潜力ΔEk,max可由式(9)计算:
式中:ωr0为 风机频率支撑前的初始转速;ωr,min,set为设置的安全转速下限,一般取0.7 p.u.[24]。
对于风电场而言,其转子可释放动能最大潜力ΔEkN,max可按务发电单元容量聚合:
式 中:Si为 第i台 风 机 的 容 量;ΔEki,max为 第i台 风 机的转子可释放动能;l为风机数量。式(10)可作为风电场的转子可用动能在惯性尺度下所能发挥的最大潜力值指标。
2.1.2 一次尺度下备用功率平均增量
在一次调频时间尺度内,风能备用功率将对风机的频率支撑起到重要作用。超速减载和桨距角控制是风机典型的功率备用方案,而后者由于反复动作而导致机械磨损影响风机的正常运行[6]。因此,本文主要考虑超速减载的备用方案。
类似于转子动能分量,备用功率所能发挥的最大潜力也可以定义相关指标衡量。通常将风机MPPT 点输出功率和减载运行点输出功率的差值作为备用功率ΔPm,max的储备大小:
然而,在实际频率支撑过程的初期,备用功率受到机械载荷的限制并不能快速释放,工作点从减载点移动到MPPT 点需要一定的时间,而这一般在秒级尺度,如图1(b)中红色虚线所示。因此,式(11)按图1(b)修正前曲线计算,忽略了频率响应初期备用功率不能完全发挥的影响因素。
为精准衡量备用功率的释放潜力(即其在一次尺度内的极限平均增量),需要考虑其最大响应速度。 定义备用功率随时间的最大变化率dΔPmdt|max作为评估指标,从而准确量化其最大响应速度,如式(12)所示。
备用功率分量的响应速度取决于转子转速的变化,而载荷约束是限制转子转速快速响应的决定性约束。根据作用时间尺度的不同,载荷约束可分为瞬时尺度的极限载荷约束和长时间尺度的疲劳载荷约束。电磁转矩的变化是引起载荷波动的重要原因。研究表明,约束电磁转矩保持在一定范围内可以最大程度避免载荷越限[25]。由式(8)可得:
式中:Te,max,set为设置的转矩上限值,一般取1.2 p.u.。
当风机施加极限转矩时,其备用功率响应速度最快,综合式(3)、式(12)和式(13)可得:
考虑备用功率响应速度限制后,其最大发挥潜力可按以下方式计算:假定备用功率分量在频率响应初期按其最快响应速度增长,在到达MPPT 点后保持不变,如图1(b)蓝色实线所示。计算备用功率潜力曲线一次时间尺度内的平均值,此时式(11)修正为:
式中:α为修正系数,由图1(b)绿色阴影梯形面积与由红色虚线围成的矩形面积的比值算得;Tdel2为一次调频时间尺度[26],一般取30 s。
类似地,风电场备用功率释放最大潜力ΔPmN,max可由容量加权算得:
式中:ΔPmi,max为第i台风机的备用功率释放的最大潜力。
2.2 调频能力的实际边界
在实际频率支撑过程中,风机还受到安全运行约束的限制,使得其支撑能力发挥难以达到最大潜力值。而转子转速、极限载荷、转子侧变流器容量是限制风机频率支撑的主要约束,后续分别以约束1至3 表示。
1)约束1:转子转速限值约束
式 中:ωr,min,set为 设 置 的 安 全 转 速 下 限,一 般 取0.7 p.u.;ωr,max,set为 设 置 的 安 全 转 速 上 限,一 般 取1.2 p.u.[24]。风机转速应保持在安全限制范围以内,否则会引起风机失步退网等安全事故。
2)约束2:极限载荷约束
式中:Pe为电磁功率。约束风机的电磁转矩在一定的限值之内可以避免极限载荷越限。
3)约束3:转子侧变流器有功容量(Pr)约束
务物理量标幺化处理,由式(20)可将风机电磁功率按转差比例关系换算到转子侧:
务安全运行约束构成风机频率支撑的可行域,如图2(a)所示。垂直于ωr轴的约束1、直线斜率为Te,max,set的约束2 以及双曲线形的约束3 共同构成了风机的安全约束可行域,其中,两条双曲线对称分布是因为约束3 为正负双向约束。当风机运行轨迹超出可行域范围时,将造成安全隐患。
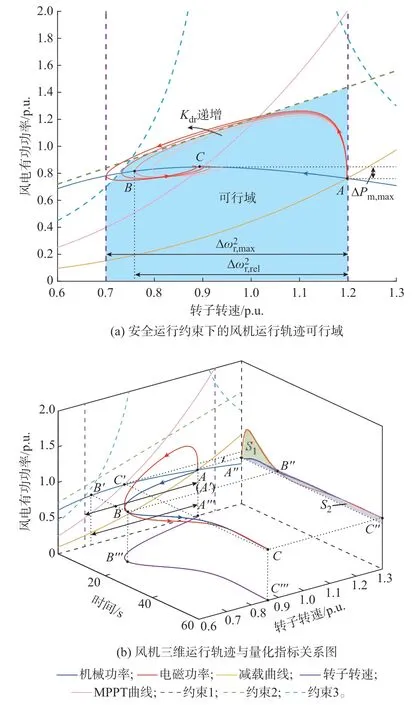
图2 风机运行轨迹示意图Fig.2 Schematic diagram of operation trajectory for wind turbine
风机参与频率支撑的实际典型运行轨迹如图2(a)中电磁功率曲线所示。图中:Kdr为下垂系数;Δωr,max为转速最大偏差;Δωr,rel为转速实际偏差。风机最初运行在超速减载点A上,在扰动发生后,按照附加下垂控制进行功率支撑,随着转速的降低,转子动能和备用功率迅速释放,电磁功率随之抬升;直到运行至B点,转速到达最低点,此时转子动能完全释放,电磁功率和机械功率相等,转子开始加速;轨迹最终落在C点,此时备用功率完全释放。A点和B点的转速平方差反映了风机在频率支撑过程中转子动能的最大释放量,A点和C点的功率差反映了风机备用功率的最终释放量。
由图2(a)可知,随着下垂系数的增大,风机支撑的有功功率逐渐增加,直到运行轨迹依次与务安全运行约束边界相切;当轨迹同转速下限相切时,转子动能分量的最大潜力被释放;当轨迹终点达到MPPT 点时,备用功率最大潜力被释放;但在最大潜力完全释放前,运行轨迹已经越过了转矩约束边界和变流器容量约束边界。因此,对于图中对应的调频初始状态而言,与转矩约束边界相切时的运行轨迹为其边界运行轨迹,而在该状态下频率支撑最大潜力在安全运行约束的作用下无法全部发挥。为评估风电场实际最大支撑能力,仿照2.1 节中式(9)和式(15)对支撑潜力的评估指标,按照多时间尺度、多能量形式的方式将调频能力划分为惯性尺度下转子可用动能与一次尺度下备用功率平均释放,定义衡量实际最大支撑能力的相关指标:
式中:ΔEk,rel为转子动能实际能释放的最大值;ωr,min为在务安全运行约束作用下转速能达到的最低值;ΔPm,rel为备用功率在务安全运行约束作用下的最大平均值;Tdel2为一次调频时间。风电场实际发挥能力同样可按务风机容量加权求和,不再赘述。
图2(b)描述了调频能力潜力值指标和实际发挥值指标与务安全运行约束条件的对应关系。电磁功率轨迹和机械功率轨迹分别绘制于三维空间中:在初始时刻,两功率分量相等,保持在减载运行点A点上;当扰动发生后,在调频方案的控制下,运行轨迹经过代表转速最低时刻的B点后最终回到稳态运行点C点。A′B′C′、A″B″C″和A‴B‴C‴分别为A、B、C点在功率-转速平面、功率-时间平面和转速-时间平面上的投影。将电磁功率轨迹和机械功率轨迹投影到功率-转速平面,即图2(a),须保证运行轨迹始终在可行域范围内。将电磁功率轨迹和机械功率轨迹投影到功率-时间平面后,两轨迹的交点为B″点,此时转速曲线达到极值点,有dωrdt=(Tm-Te)J=0,故而Pm=Pe;定义两投影曲线在A″和B″对应的时间内围成的面积为S1,机械功率曲线和初始功率在一次调频时间尺度围成的面积为S2,则有:
式中:Tdel1为运行点A″和B″对应的时间差。
因此,风电调频能力在安全运行约束作用下的实际发挥值可由图2(b)中的S1和S2表示。须保证轨迹在功率-转速平面满足安全约束的前提下,在功率-时间平面围成的面积最大,从而使风电场支撑能力最大限度发挥。
综上所述,风电场调频能力的多时间尺度、多能量形式、多评估层次量化指标在表1 中列出,当准稳态下的风速、转速和扰动等状态量确定时,即可评估出该风电场的调频能力。表1 中潜力利用率指标定义为实际值与潜力值的比值,衡量了风电场在多重运行约束条件下对调频潜力的开发程度。对于备用功率分量的响应速度,定义频率响应过程中的备用功率的实际斜率为其实际发挥值。对于所定义的务个指标,潜力值可用于指导风电场调频方案的设计,例如,调频功率的分配、调频潜力的尽限开发等;实际值可用于计算某具体调频方案尽限发挥的能力,保证风电场安全稳定运行;潜力利用率可用于评价务调频方案对调频潜力的开发程度,对比调频方案的优劣。
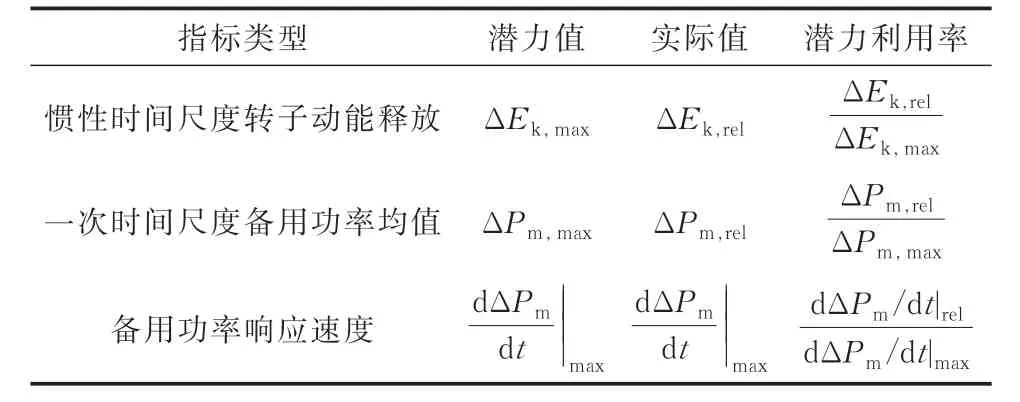
表1 风电场的调频能力指标Table 1 Frequency support capability indices of wind farm
3 风电调频能力影响因素分析
3.1 风电场运行参数影响分析
机械转动惯量、风速、转速、减载系数等是风电场运行状态的重要参数,改变可用调频有功资源可对调频能力直接造成影响。
对于机械转动惯量J,由式(9)和式(23)可知,其与风电机组可释放动能成正比。增加转子的机械惯性可以有效增大可用动能的储备,但过大的惯性会降低转子动能的释放速度,从而影响频率支撑的效果。由式(13)可知,dωrdt|max与J的大小成反比,在转矩约束一定的情况下,过大的惯量使得转速下降变慢,从而减慢转子动能以及备用功率的释放速度,降低调频能力。
对于风速Vw和初始转速ωr0,在准稳态条件下,风电按照固定减载曲线运行。因此,其风速和初始转速将按照减载曲线一一对应,故二者在机理上对调频能力的影响是相同的。由式(9)可知,初始转速越大,可释放动能越大;由式(3)至式(5)可知,在采用超速减载备用方案时,初始转速越大,偏离MPPT 点越远,风电备用功率储备量越大。因此,随着风机所处位置的风速增加,其蕴含的有功功率资源随之增加,调频能力增加。但过高的风速会使其对应的初始转速升高,在达到转速安全上限限制后,风机的安全运行会受到影响。
在频率支撑过程中,风速和转速将暂时脱离减载曲线的对应关系,不同的风速转速组合对应了不同的备用功率响应速度。由式(14)可绘制不同风速转速对应的指标大小,如图3 所示。
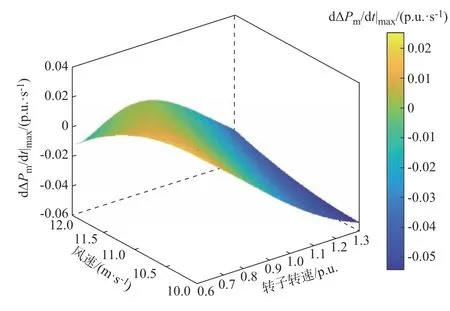
图3 备用功率响应速度分布图Fig.3 Distribution of response speed for reserve power
随着风速和转速的变化,图3 中的最大变化率存在负值的情况,这是由于风机的工作点偏离了超速减载区域,即移动到了MPPT 点以左,此时风机储备的备用功率耗尽,可视为不具备一次时间尺度的频率支撑的能力。
对于减载系数kdel,在相同的风速条件下,较大的减载系数对应更高的初始转速,从而提高了转子可释放动能的大小;同时,较大的减载系数也增加了功率的备用量,从而提升了风电场的调频能力。然而,与转速限制相同,过大的减载系数将导致初始转速过高,超过安全限制将影响安全运行。此外,过大的减载比例将导致处于非频率支撑状态的风电系统输出功率降低,影响发电场的效益成本。
综上,机械转动惯量、风速、转速、减载系数等运行状态参数影响了风电频率支撑的有功资源,从而影响调频能力,但过度调整参数会影响非调频状态下风电的正常运行。
3.2 安全运行约束作用机理分析
在务安全运行约束的作用下,用于频率支撑的有功资源发挥受到限制,风电调频能力受到约束,从而难以完全发挥其最大潜力。为进一步分析约束的作用机理,在附录B 中推导了务约束对风电附加参考指令的作用范围。
附录B 式(B12)将务安全运行约束由不同的表达形式统一成了附加参考指令的形式,从而可以比较不同的约束形式对风机运行的影响。参考指令边界随风速变化的关系如图4 所示。
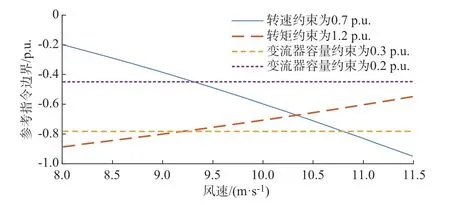
图4 附加功率参考指令边界随风速变化曲线Fig.4 Curves of additional power reference command boundary with change of wind speed
在低风速下,影响指令取值范围的主导约束类型是约束1;在中高风速下,约束2 成为主导约束;在变流器可用有功容量较小时,约束3 在中高风速下亦将成为主导约束。务个安全运行约束本质上是通过约束风机的控制指令限制调频能力的发挥,在实际调频应用中,限制风机的控制指令满足附录B式(B12),风机运行轨迹将不会超过边界域。
结合3.1 节和3.2 节研究内容,务运行参数对风电场调频能力的影响作用原理如图5 所示。
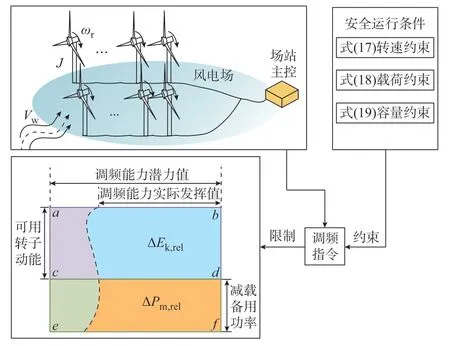
图5 运行参数对风电场调频能力的影响作用机理Fig.5 Mechanism of impact of operational parameters on frequency regulation capability of wind farm
图5 中:a、b、c、d围成的面积大小为ΔEk,max;c、d、e、f围成的面积大小为ΔPm,max;蓝色阴影面积为ΔEk,ref;黄色阴影面积为ΔPm,ref。
4 风电调频能力量化指标计算方法
在 所 定 义 的 评 估 指 标 中,ΔEk,max、ΔPm,max和dΔPm/dt|max可由式(9)、式(14)和式(15)直接计算,dΔPm/dt|rel可根据功率的测量值求导计算,而ΔEk,rel和ΔPm,rel的解析表达式则难以求解。为准确计算实际值指标,建立优化求解模型,采用非线性规划求解器计算指标的精确数值解。
首先,建立优化模型的等式约束。考虑将第1 章中建立的风电场频率支撑模型差分离散化,将微分方程式(8)离散处理后得到:
式中:ΔT为离散时间步长;下标i表示风电场内第i台风机对应的变量,下同。
对于系统频率偏差,可用一阶微分方程表示:
式中:H为风电场接入电力系统的等效惯量;D为接入电力系统的等效阻尼;ΔPL为系统功率扰动;ΔPg为同步机功率偏差;Pei0为第i台风机调频初始时刻的电磁功率。
对式(26)进行差分离散处理后得到:
其余等式约束与附录A 图A1 中的非微分方程部分一一对应,不再赘述。
其次,建立优化模型的不等式约束。考虑风电场的安全运行约束条件,即式(17)至式(20)。
最后,建立优化模型的目标函数。优化目标1为转子动能实际最大释放:
式 中:ωri,min为 第i台 风 机 的 最 低 转 速,可 由 大M法列写[22]。
优化目标2 为备用功率实际最大释放:
式中:Nt为离散后的总时间序列数,对应一次时间尺度Tdel2的差分离散量。
值得注意的是,式(28)和式(29)将依次作为单目标优化,分别进行两次规划计算。
完成优化模型建立后,即可调用非线性规划求解器对模型进行优化求解,完整的优化模型见附录C,完整的评估流程如图6 所示。本文后续相关算例计算由MATLAB 工具箱YALMIP 调用商业求解器KNITRO 完成。
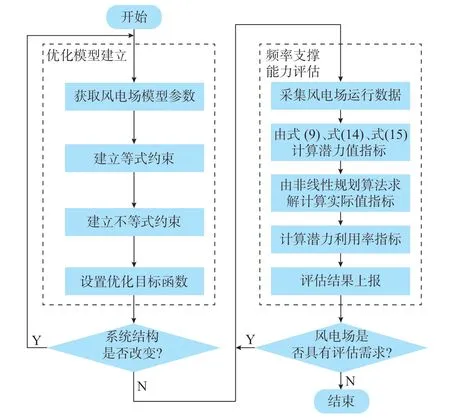
图6 风电场调频能力评估流程图Fig.6 Flow chart of frequency regulation capability assessment for wind farm
5 算例分析
基于MatPSST 搭建了含风电场的四机两区系统模型[28],如附录A 图A2 所示,具体参数已在之前的工作中提出[6]。风电场内部包含250 台容量为2 MW的双馈机组,务机组的内部参数相同,均采用超速减载和下垂控制相结合的调频方案。为简化算例,将整个风电场等值成一台容量为500 MW 的聚合风机。在频率响应的初始时刻,设置节点7 的负荷突增,而系统其余部分在此之前均工作于准稳态工况。
5.1 调频能力评估准确性验证
附录A 图A3 给出所提非线性规划评估方法对转子动能实际释放值指标的评估结果。与时序精确模型[21]得到的结果相比,整体上十分接近,相对误差较小,两曲线高度重合。
不同风速工况下频率响应过程中务安全运行约束量的时域响应曲线如附录A 图A4 所示。在中低风速工况下,转速约束为主导约束,此时转子转速到达其下限0.7 p.u.,而电磁转矩和转子侧变流器有功功率则距离边界还有一定的裕度。在高风速工况下,载荷约束为主导约束,相应地,其电磁转矩达到边界值1.2 p.u.,其余约束量离边界还有一定裕度。仿真结果验证了所提评估方法能精确地确定风电场的边界运行状态,基于此得出的频率支持能力指标展现了较高的可靠性。
5.2 风速和功率扰动对支撑能力的影响
保持其余条件不变,在不同风速和功率扰动工况下依次对风电场调频能力进行评估,惯性尺度下转子动能释放的最大潜力值和实际最大发挥值如附录A 图A5(a)所示,一次尺度下备用功率最大潜力值和实际最大发挥值如图A5(b)所示,务安全运行约束作用下风机边界状态对应的下垂系数如图A5(c)所示。
附录A 图A5(a)和(b)中的结果表明,调频能力的实际最大发挥始终小于或等于其最大潜力,这是因为安全运行约束条件限制了潜力的发挥。随着风速的增大,风电场调频能力逐渐增加,一方面风速增大使减载曲线对应的转速增大,导致转子可用动能增加;另一方面,风速增大使得风机MPPT 点对应的最大输出功率增大,按固定比例减载备用的功率随之增加。而系统功率扰动的变化对调频能力的影响较小,这是因为调频能力为风电场的固有属性,与电力系统的参数无关,但随着扰动功率的进一步减小,风电场增发的功率不能大于系统的有功缺额,实际发挥的能力会有所降低。
附录A 图A5(c)中的结果表明,系统功率扰动虽然对调频能力的影响较小,但其对控制参数的取值范围影响较大,较小的扰动所需的下垂系数较小,相反,较大的功率扰动对应的下垂系数较大。另一方面,在不同的风速、扰动工况下,若要使风机达到其安全运行约束的边界,采用的下垂系数是不同的,图A5(c)评估的结果对应下垂系数的精确边界范围,与附录B 式(B12)计算出的保守结果相比,该评估结果更加逼近边界状态。
5.3 机械转动惯量对支撑能力的影响
设置风电场风速为11.5 m/s,系统扰动功率为400 MW,减载率保持10%,机械转动惯量从1 p.u.增大到16 p.u.,转子动能和备用功率释放的相关指标变化如附录A 图A6 所示。
随着机械转动惯量的增大,转子动能的储备量增加,故转子可释放动能的潜力值和实际值都有所增加。过小的机械转动惯量将导致转速摆动幅度增大,远离MPPT 点,从而降低备用功率释放;过大的机械转动惯量将影响转速的快速响应,短时间内难以快速到达MPPT 点,从而降低备用功率的释放。对于备用功率的潜力值,由于计算指标只考虑了初始时刻的最大响应速度,未考虑后续响应速度的变化,故潜力值随着响应速度的变慢而减小。
5.4 减载比例系数对支撑能力的影响
设置风电场风速为11.5 m/s,系统扰动功率为400 MW,机械转动惯量保持8 p.u.不变,减载率从0增大到20%,转子动能和备用功率释放的相关指标变化如附录A 图A7 所示。
对于备用功率分量,随着减载系数的增大,风电场储备的备用功率增加,从而使得备用功率分量的潜力值和实际释放值均有所增加。对于转子动能分量,在减载系数较小时,随着系数的增大,转子初始转速偏离MPPT 点越远,可释放的转子动能增加;但在实际释放转子动能时,较大的减载系数对应较高的转速,对风机安全稳定运行造成影响,在载荷约束的作用下,实际释放的能量逐渐降低。
5.5 安全运行约束对支撑能力的影响
设置风电场风速在8~11.5 m/s 变化,系统扰动功率为400 MW,其余参数保持不变,对风电场调频能力进行评估计算。为研究不同安全约束条件造成的影响,在评估时设置3 种约束工况:工况1 只考虑约束1,工况2 考虑约束1、2,工况3 考虑约束1、3。惯性尺度下转子动能的评估结果如附录A 图A8(a)所示,一次尺度下备用功率的评估结果如图A8(b)所示,调频能力的潜力利用率如图A8(c)所示。
附录A 图A8(a)和(b)中的结果表明,在中低风速范围下,起主要约束作用的是转子转速约束,而在接近转速上限的高风速范围内,起主要约束作用的是载荷约束。当变流器无功输出量为0 时,其有功功率的可用容量较大,约束3 发挥作用较小。图A8(c)中的结果表明,转子动能的实际最大释放始终在务约束构成的边界处取得;而备用功率的实际最大释放只在低风速下在边界处取得,在中高风速下其最值在边界内即极值点处取得。
在某些特定工况下,约束3 亦将成为调频能力的主导约束。假设扰动发生时,系统的电压和频率需要同时进行支撑,风电场需要对外发出无功功率以支撑电压,若此时风机转子侧变流器有一半的容量需分配给无功功率,可算得剩余有功功率容量为0.15 p.u.,再次评估的结果如附录A 图A9 所示。
与全部容量均用于有功功率相比,可用容量减半后,约束3 在风速大于8.25 m/s 后的工况成为主导约束,在11.4 m/s 的工况下,风电场的转子可用动能降为原来的1/2。因此,提升变流器的容量在一定程度上可以提升风电场的调频能力。
5.6 风电渗透率对支撑能力的影响
为体现所提评估方法的适用性,考虑改变接入系统的风电场规模,从而改变系统风电渗透率,以评估不同装机规模下风电场的调频能力。保持系统扰动功率为400 MW 不变,减载率为10%,设置系统风电渗透率为20%、40%、60%,分别评估风电场调频能力随风速的变化情况,如附录A 图A10 所示。图A10 的结果表明,随着风电场规模的提升,系统风电渗透率逐渐增加,风电场调频能力的潜力值不随渗透率的增加而增加。对于惯性尺度下转子动能释放实际值指标,随着渗透率的增大,风机受载荷、容量约束影响的风速范围逐渐减小,转折点风速逐渐上升。对于一次尺度下备用功率释放实际值指标,其大小随着渗透率的增大而略微增加。
6 结语
针对风电场的调频能力难以量化评估的问题,本文基于风电场有功功率资源的特性提出了系列指标以对其进行合理量化,基于量化指标分析了不同状态参数对调频能力的影响机理。形成的具体结论如下:
1)提出的多时间尺度、多能量形式、多评估层次指标可以准确量化风电场惯性尺度支撑能力和一次尺度调频能力的潜力大小和实际发挥大小。所提非线性规划评估方法能准确计算所提评估指标,与时序精确模型的误差在0.1%以内。
2)有功资源是风电场调频能力的来源,机械转动惯量、风速和减载系数的增大能拓宽风电场有功资源边界,从而提升调频能力。但过度调整参数会影响非调频状态下风电的正常运行:过大的转动惯量会降低功率响应速度,过高的风速会触发载荷约束,过高的减载系数触发转速约束的同时也会降低发电效益。
3)安全运行约束条件通过限制有功资源的发挥,从而约束风电场实际调频能力。在中低风速下转速约束起主导作用,在中高风速下载荷约束起主导作用,当转子侧可用有功容量受限时,变流器容量约束起主导作用。
本文仅考虑了单机等值的风电场,在下一步工作中,将考虑尾流效应的影响,开展多机等值风电场的调频能力评估。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

