基于GNSGA?Ⅱ算法的线圈优化设计

姜建国 佟麟阁 喻明斐

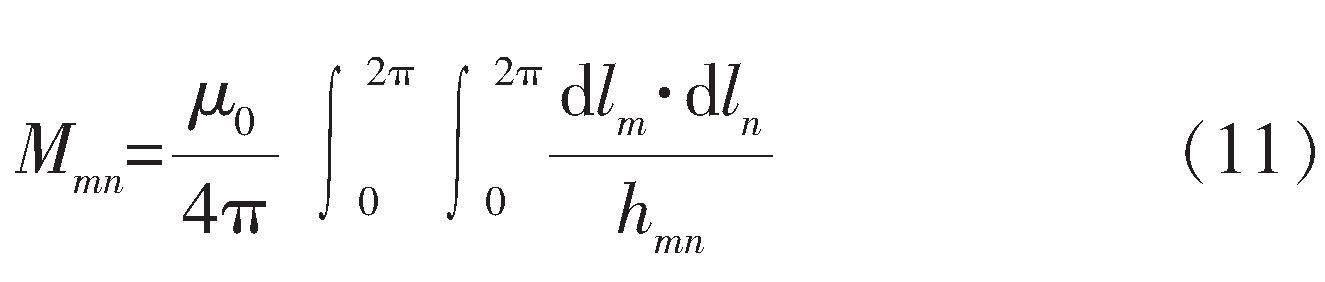
摘 要 在电动汽车无线充电技术中，充电线圈的性能直接影响系统的整体传输性能。在分析常用线圈形状的基础上，引入拉梅曲线方程，设计了一种新型超圆角方形线圈；对耦合电路进行理论分析，得到优化目标传输效率和功率密度与待优化参数之间的关系；利用改进的多目标优化算法（GNSGA?Ⅱ）进行线圈的参数优化，得到一组最优的参数解用于工程设计。该方法相比于传统有限元仿真计算法，具有节省时间的优点，优化设计结果表明该方法具有有效性。

关键词 多目标优化设计 GNSGA?Ⅱ算法 无线充电 超圆角方形线圈 参数优化 拉梅曲线方程

中图分类号 TM72   文献标志码 A   文章编号 1000?3932（2024）01?0077?09

电动汽车有线充电形式存在充电不便、操作繁杂、复杂天气充电不安全等问题［1～3］，而无线充电恰好可以解决此类问题，因此，研究无线充电在电动汽车领域的应用具有很高的实际价值和现实意义［4，5］。

在磁共振无线电能传输（Magnetic Coupling Resonant?Wireless Power Transfer，MCR?WPT）技术中，线圈是整个无线充电系统设计的核心，直接决定充电系统的传输性能［6，7］。合理优化线圈参数，可以保证较高的传输效率和较大的功率密度。在设计过程中，使用优化算法可以简化设计步骤，加快线圈优化进程。线圈设计一般具有复杂性，可将线圈优化定义为一个多目标多参数问题，这类问题通常是通过使用多目标智能算法解决的。文献［8］采用遗传算法优化线圈结构，提高了线圈的耦合系数；文献［9］将禁忌搜索算法与有限元仿真相结合，优化了耦合系数和线圈费用两个目标；文献［10］改进了粒子群优化算法（PSO），减少了圆形无线电能传输技术（Wireless Power Transfer，WPT）耦合器中的优化参数，在相同的优化性能下，该方法降低了时间成本；文献［11］采用粒子群优化算法和有限元仿真相结合的方法，实现了传输效率、功率密度和线圈重量3个指标的优化设计；文献［12］采用有限元仿真模型，通过参数扫描反复计算，实现了传输效率和功率密度两个指标的优化设计。上述文献在优化设计过程中，并未考虑线圈形状对系统参数的影响。因此，笔者基于拉梅曲线方程设计了一种新型超圆角方形线圈，采用GNSGA?Ⅱ算法对线圈参数进行优化设计，得到了一组最优参数解。

1 线圈参数设计

1.1 线圈形状设计

目前，在无线充电线圈上应用的线圈形状有许多，但是大多数学者是直接选择某一形状后使用，未就线圈形状对线圈参数的影响进行定量分析。

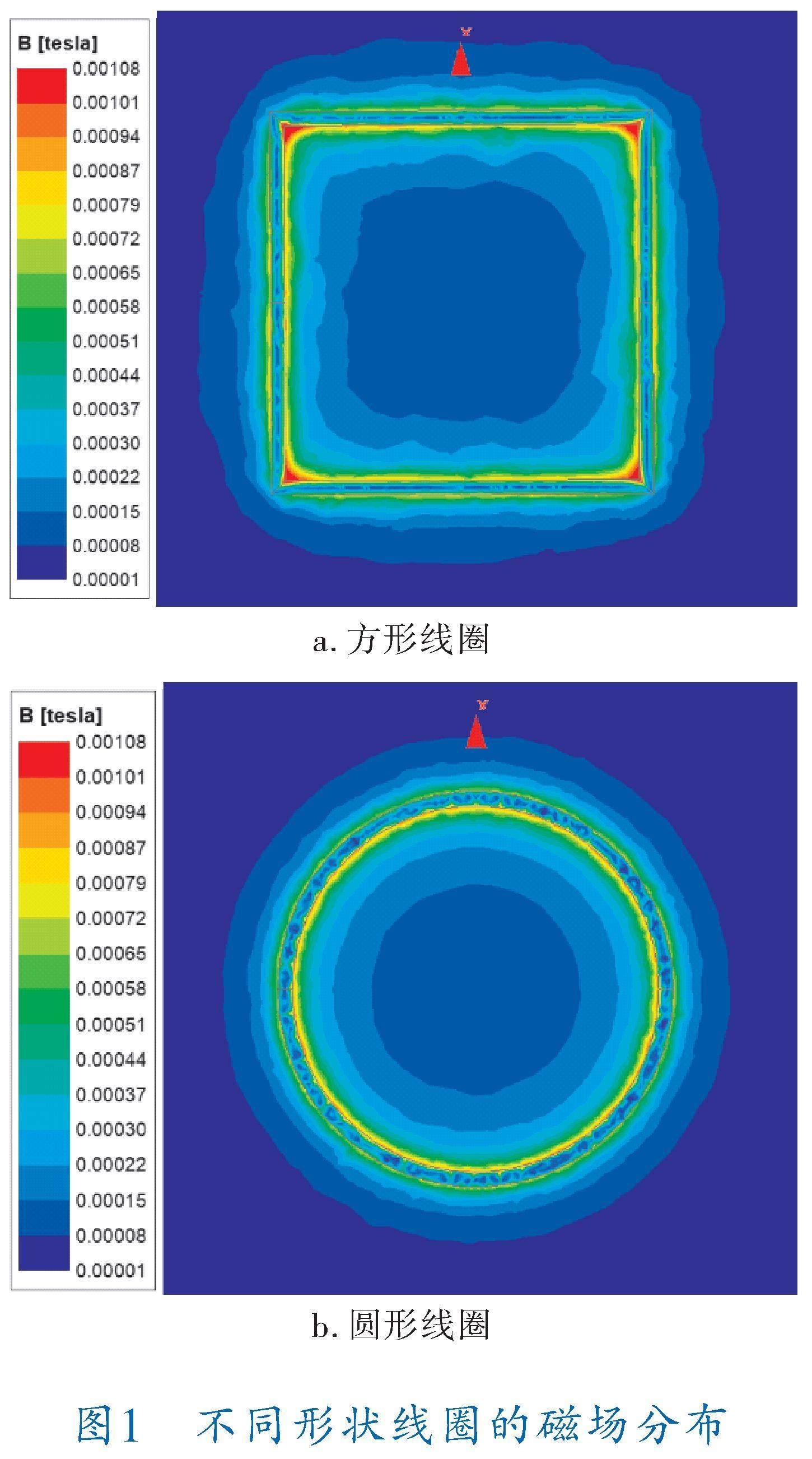
线圈的基础形状主要有圆形和方形，对这两种形状的单匝线圈模型进行特性分析，在模型中，圆形线圈直径和方形线圈的边长相等，均为10 cm，设置系统电流10 A、频率85 kHz，发射线圈与接收线圈之间的耦合距离5 cm。方形线圈和圆形线圈的磁场分布如图1所示，仿真结果见表1。从表1可以看出，圆形线圈具有良好的磁场分布，但是电感较小；方形线圈虽然具有较大的电感（电感值大意味着线圈可以承受更大的功率），但是4个角漏磁较为严重。因此，提出一种综合两者优点的线圈，通过引入拉梅曲线方程，设计出一种超圆角方形线圈。

拉梅曲线是在笛卡儿坐标系下满足某特定方程式的点的集合，最初是由法国数学家加布里埃尔·拉梅对椭圆方程进行扩展而得，其方程式为：

其中，a、b为曲线的半直径。

式（1）的解是一个在x∈［-a，+a］，y∈［-b，+b］的长方形内的封闭曲线，分类讨论如下：

a. 当0

b. 当n=1时，曲线形状为菱形，4个顶点为（±a，0）及（0，±b）；

c. 当1

d. 当n=2时，曲线形状为椭圆（如果a=b则为圆形）；

e. 当n>2时，曲线形状类似四角有圆角的长方形，曲线的曲率在（±a，0）、（0，±b）；

f. 当n=4时，曲线为方圆形；

g. 当n→∞时，曲线形状为矩形。

本研究中，取a=b，将n>2的曲线形状命名为超圆角方形，设定n的范围为［2，10］，其值均取整数，其中n=2时，线圈形状为圆形；n→∞时，线圈形状为矩形。建立9个超圆角方形线圈模型，设置系统电流为10 A、频率85 kHz，得到的仿真结果如图2所示。

通过分析可知，随着n值的不断增大，线圈的电感是逐渐增大的，但是耦合系数是先增大后减小。同时，考虑到要尽可能减小损耗，所以取n=5时，线圈具有较高的耦合系数、较大的电感和较低的损耗，并且线圈还具有良好的磁场分布，此时该形状的线圈最优，其磁场分布如图3所示。

1.2 电路理论分析

磁耦合谐振式无线充电电路原理如图4所示，主要包括发射线圈电感L、电阻R和补偿电容C；接收线圈电感L、电阻R和补偿电容C；I和I分别是发射线圈和接收线圈中的电流；R为系统负载；U为电源电压；M为线圈互感。

线圈效率η的计算式为：

其中，Q、Q是两个线圈的品质因数；ω为角速度。

由式（2）～（5）可知，线圈效率与线圈的自感、电阻和互感有关。

1.3 线圈互感的计算

两单匝同轴线圈间的互感如图5所示。首先求解发射线圈中由外向内的第m匝线圈以及接收线圈中由外向内的第n匝线圈之间的互感，其半直径分别记为a和a，分别以两线圈中心为原点建立坐标系［13］，如图5所示。其中，线圈m、n中的微元分别记作dl、dl；γ、δ分别为微元dl和dl与x轴的夹角；h为两线圈之间的垂直距离；h表示微元dl和dl之间的距离；d为线径；p为发射线圈匝间距；r和r分别为发射线圈和接收线圈的外半径。

由图5可得：

两单匝线圈的半直径可分别表示为：

a=r-（m-1）（d+p）（9）

a=r-（n-1）（d+p）（10）

其中，p为接收线圈匝间距。

由诺依曼公式可知，两同轴单匝线圈间的互感M可表示为：

其中，μ为真空或空气磁导率，取4π×10-7 H/m。

同轴平面线圈间的互感M可以看作是两线圈内部各单匝线圈互感之和：

1.4 线圈自感的计算

线圈自感可以近似看成是其内部每匝线圈的自感以及内部任意两匝线圈之间的互感之和［14］。其中，两匝线圈间的自感示意图如图6所示。

则线圈自感表达式为：

其中，N、N、N∈N；k′为线圈匝数。

1.5 线圈电阻的计算

线圈导线一般采用铜导线或者多股利兹线。多股利兹线是由多股漆包线绞合在一起的导线，减小了集肤效应带来的损耗，而且可以基本消除各相邻导线的临近效应。相比于铜导线，利兹线优势较为明显，因此一般选用多股利兹线作为电动汽车无线充电线圈的导线。

本研究中，使用800股线径为4 mm的利兹线，其交流电阻R估计计算式为：

其中，K为绞合系数，这里取1.03；ρ为电导率，其值为1.72×10-8 S/m；l为线圈的总绕线长度；N为股数；d为单股线的线径；系统的工作频率f为85 kHz。

线圈的总绕线长度l的计算式为：

其中，a为第k′匝线圈的半直径，r为线圈外半径，w为线圈匝间距。

2 线圈参数多目标设计方法

无线充电线圈的优化设计是一个多目标多参数优化问题。在磁耦合器中，线圈是电动汽车无线充电系统能量传输的基本载体，线圈的形状、结构和尺寸直接影响磁耦合器的电气参数，如自感、互感及耦合系数等，同时也会影响磁耦合器的磁场分布特性和空间偏移特性。因此，在设计磁耦合器时需要对线圈进行充分的结构分析和优化，以实现最佳的性能。

相比于传统的试凑法，采用优化算法进行线圈参数优化设计可以节省大量的时间成本。因此，需要建立准确的目标函数方程，使用优化算法得到更为精确的解。本研究通过改进NSGA?Ⅱ算法来提高优化参数解解集的质量。

在无线充电系统中，功率密度和传输效率是系统评价性能是否良好的两个重要参数，传输效率越高，系统损耗则越小，这样无线充电系统的经济性更好，因此将系统传输效率作为一个目标函数。由于接收线圈安装在电动车底部，受到汽车自重和内部空间大小的限制，接收线圈需设计得精致小巧，以节省空间，又不影响功率传输。因此将无线充电线圈的功率密度作为第2个目标函数。

2.1 优化目标函数

建立以无线充电线圈的传输效率和功率密度为优化目标的目标函数。

2.1.1 传输效率

通过之前的理论分析可知，系统传输效率与线圈耦合系数k以及线圈的品质因数Q有关，其目标函数为：

2.1.2 功率密度

在设计中，提高线圈的单位面积传输功率可以减小接收线圈的重量和体积，这对电动汽车而言，可以节省更多的空间来安装电池组或其他设备。将λ定义为接收线圈单位面积的传输功率，其计算式为：

其中，P为系统设计额定功率；S为接收线圈的面积。

2.2 约束条件

在设计优化线圈过程中，需要考虑其他因素对线圈的约束。首先考虑线圈的安装环境，其线圈半直经不能超过车自身的宽度，而且线圈的匝间距应该大于导线材料的直径，其中导线线径d为4 mm。设发射线圈的外半径为r，匝数为N，匝间距为w；接收线圈的外半径为r，匝数为N，匝间距为w，参数取值见表2。

2.3 优化模型

结合以上分析，本研究的优化问题可以表示为：在满足基本线圈尺寸的前提下，以传输效率最高、功率密度最大为目标，确定发射线圈和接收线圈的尺寸、匝数和匝间距；设定传输效率的倒数和功率密度的倒数为目标函数，则线圈多目标优化的模型如下：

在上述目标优化问题中，优化参数为6个变量的集合，目的是为了寻找一组使所有目标尽可能达到最优的解，这个解称为Pareto最优解，所有的Pareto前沿构成Pareto最优解集。

3 基于GNSGA?Ⅱ算法的磁耦合机构优化设计

求解多目标优化问题过程中，目标函数之间往往是互相矛盾的，因此需要计算出满足这些目标函数的相对最优的Pareto解集。

一般多目标优化算法有MOGA、NSGA、SPEA等。与NSGA算法相比，NSGA?Ⅱ算法通过采用精英保留策略扩大了采样空间，防止优良个体丢失，保证了种群的多样性，提高了算法的运算速度和鲁棒性，使最优解能够分布在Pareto前沿。然而该算法依然存在缺陷，NSGA?Ⅱ算法所提出的个体拥挤距离计算方式存在局限性，从而导致种群的分布不均匀。

3.1 NSGA?Ⅱ的拥挤机制缺陷

NSGA?Ⅱ算法通过计算个体拥挤距离建立拥挤度排挤机制。在每次迭代时，通过分层排序计算出种群个体之间的距离，在同一层级中，将拥挤距离大的种群个体筛选出来，继续进行下一次迭代。因此，该机制存在以下缺陷：

a. 无法从整个种群分布的角度看待个体周围的密集程度；

b. 基于拥挤距离的排挤机制无法准确测量同一层级中相邻个体的密集程度。

由此可知，NSGA?Ⅱ算法无法准确计算个体的密集程度，导致最优解集分布不均匀，而且也会出现解集的“中断”。

3.2 GNSGA?Ⅱ算法个体邻域的构建

基于对NSGA?Ⅱ算法缺点的分析，引入DBSCAN算法中的邻域思想［15］改进NSGA?Ⅱ算法的拥挤机制，形成GNSGA?Ⅱ算法。DBSCAN算法是一种基于密度的聚类算法，其核心思想是用一个点的邻域内个体数量来衡量个体周围的密集程度，此点密度半径以内所有点的集合称为该点在此密度半径下的邻域。

设x∈X，称N（x）={y∈X：d（y，x），θ}为x的θ邻域，显然，x∈N（x）。

目标函数的种群密度半径计算式为：

其中，F和F表示种群在目标函数下F（x）的最大值与最小值；m为种群大小。因此，θ就可以表示为在目标函数F（x）下两个个体间的平均距离，这就可以保证种群个体的均匀分布。

GNSGA?Ⅱ算法的流程如图7所示。

3.3 GNSGA?Ⅱ算法的测试与分析

通过选取两个两目标测试函数ZDT1、ZDT2和一个三目标函数DTLZ7对GNSGA?Ⅱ算法进行测试，算法参数设置为：种群规模100，进化代数500，交叉概率0.9，变异概率0.1。测试结果如图8～10所示，可以看出，相比于NSGA?Ⅱ算法，GNSGA?Ⅱ算法的Pareto前沿具有更好的分布性。

4 线圈优化结果分析

接下来使用GNSGA?Ⅱ算法对磁耦合线圈参数进行求解，在其目标函数的约束条件内，寻找最佳匹配的磁耦合线圈参数，使MCR?WPT系统的传输效率和功率密度相对最优。设置GNSGA?Ⅱ算法的交叉概率为0.8、变异概率为0.1、种群大小为200、迭代次数为200。仿真得出的Pareto曲线如图11所示，可以看出，Pareto前沿逐渐降低，前沿分布平滑均匀，并未陷入局部最优。

效率与功率密度的关系如图12所示，可以看出，系统的输出效率和功率密度之间呈负相关，在耦合线圈不同的匹配参数下，随着传输效率的提升，功率密度会减小。

测试的部分前沿解列于表3，可以看出，发射线圈变化较小，随着接收线圈尺寸的减小和匝数的减少，传输效率逐渐减小，功率密度逐渐增加。

在实际工程中，需要根据设计者需求选择一组最优设计值。对于参数解集，使用加权归一化处理，得到最优解。此处传输效率的权重选择0.8，功率密度的权重选择0.2，其加权归一化公式为：

其中，F为参数解集中的第i个解；F（n）和F（n）为第n个目标的最小值和最大值；G为目标权重；n为待优化目标个数。

根据上述分析得出1组最优解，详见表4。

5 结束语

以电动汽车无线充电系统的磁耦合线圈为研究目标，进行优化设计。首先引入拉梅曲线方程设计新型超圆角方形线圈，该线圈具有良好的磁场分布和较优的性能；接着建立无线充电系统的电路模型，对影响优化目标性能的3个电气变量参数（线圈自感、线圈互感和线圈电阻）进行理论分析；然后以系统传输效率和功率密度为优化目标，以发射线圈和接收线圈的外半径、匝数和匝间距的取值范围作为约束条件，建立无线充电线圈多目标优化数学模型。最后，使用GNSGA?Ⅱ优化算法对线圈进行优化设计，在目标函数的约束条件下，得到了Pareto最优解集。根据设计者使用的实际情况，对解集进行了加权归一化处理，得到了一组最优设计值，可为工程设计提供参考。

参 考 文 献

［1］ 李阳，石少博，刘雪莉，等.磁场耦合式无线电能传输耦合机构综述［J］.电工技术学报，2021，36（S2）：389-403.

［2］ 廖力，刘坤，吴铁洲.电动汽车无线充电系统阻抗补偿方法研究［J］.电源技术，2021，45（3）：374-377.

［3］ 马精慧，宋杨.基于线性变参数模型的汽车移动无线充电系统研究［J］.电子测量技术，2018，41（4）：16-23.

［4］ 崔淑梅，宋贝贝，王志远.电动汽车动态无线供电磁耦合机构研究综述［J］.电工技术学报，2022，37（3）：537-554.

［5］ 刘宝航，王秉森，李子奇.磁耦合谐振式无线电能发射系统的设计与实现［J］.电子测量技术，2019，42（10）：28-32.

［6］ 吴理豪，张波.电动汽车静态无线充电技术研究综述（上篇）［J］.电工技术学报，2020，35（6）：1153-1165.

［7］ 吴理豪，张波.电动汽车静态无线充电技术研究综述（下篇）［J］.电工技术学报，2020，35（8）：1662-1678.

［8］ WANG S C，XU C，WEI B，et al.Analysis and optimization of coil structure of magnetic circuit mechanism for electric vehicle wireless charging system［J］.IOP Conference Series：Earth and Environmental Science，2021，675（1）：012098.

［9］   HASSAN M A，HAILAT N，BADAWI N，et al.A wireless power transfer system with optimized circuit parameters using genetic algorithm［J］.International Renewable Energy Congress，2017：386-389.

［10］   BOSSHARD R，KOLAR J W，MUHLETHALER J，et al.Modelingand α?η?pareto optimization of inductive power transfer coils for electric vehicles［J］IEEE Jounal of Emerging and Selected Topics in Power Electronics，2015（1）：50-64.

［11］   YILMAZ T，HASAN N，ZANE R，et al.Multi?objective optimization of circular magnetic couplers for wireless power transfer applications［J］.IEEE Transactions on Magnetics，2017，53（8）：1-12.

［12］   BANDYOPADHYAY S，PRASANTH V，BAUER P，et al.Multi?objective optimization of a 1 kW wireless IPT system for charging of electric vehicles［C］//2016 IEEE Transportation Electrification Conference and Expo.Dearborn，MI，USA：ITEC，2016：1-7.

［13］ 吴昕，何小斌，蓝建宇，等.基于螺线方程的MCR?WPT系统线圈设计［J］.电源学报，2021，19（5）：75-82.

［14］ 陈忠华，卢韦，时光，等.无线电能传输系统的线圈参数及耦合系数研究［J］.高压电器，2019，55（4）：205-210.

［15］ 王光，林国宇.改进的自适应参数DBSCAN聚类算法［J］.计算机工程与应用，2020，56（14）：45-51.