基于扩充参数平面法的PID控制及陷波器设计

章国光,燕波宇,陈超凡,王晓光

(湖北工业大学电气与电子工程学院,武汉 430070)

0 引言

伺服驱动系统通常由伺服电机、联轴器、传动轴和机械负载组成。为提高系统动态响应和节约能源,驱动部件通常采用小型轻量化设计,但该设计会减小传动装置刚度,降低固有频率,当固有振荡频率位于调速系统的工作频带范围内,轴系就有可能出现机械振荡[1]。机械振荡除了会发出声学噪声形成噪声污染外,还会对机械传动装置造成严重的损害,影响其使用寿命;另外,还会引发控制系统中的控制量振荡,使得控制的稳定性以及可调整性受到制约[2-3]。因此,机械振荡的研究以及抑制方法已成为高性能伺服驱动的重要研究课题之一。

丁有爽等[4]采用双闭环的速度环和电流环控制策略对电机驱动弹性负载系统进行控制,通过与传统刚性负载系统对比,表明弹性负载会产生谐振,考虑弹性特性设计,系统响应特性好。龚文全、龙丁等[5-6]针对使用常规陷波器存在的相位滞后情况,分析了陷波器对系统性能的影响,在常规二阶陷波滤波器结构的基础上,提出了减小陷波器相位滞后的改进策略,改善陷波器加入系统后造成的相位裕度损失。CHEN等[7]针对系统谐振频率发生偏移时,使陷波器由于错误的陷波频率而引起频率较低的振荡,甚至使谐振更严重的问题,提出了一种适用范围更广、鲁棒性更强的无振荡回弹陷波滤波器调谐策略。

传统陷波器设计方法通过系统的开环特性,针对系统的谐振频率对陷波器进行设计,旨在通过对陷波器本身的改进提升系统性能。但将系统控制器和陷波器分别设计,未有效考虑陷波器设计和系统控制的匹配设计问题,不利于系统的优化。

工业伺服系统中位置控制最为常用,通常采用内外环控制器的形式,并通过先内环后外环的方式来调节参数[8-9];这种内外环独立调节方式,可保证系统的稳定,但难实现系统性能的最佳。另外,基于遗传算法的参数自调节虽有效,但调节参数的计算复杂,直观性稍差[10]。

本文提出三参数设计的扩充参数平面法,通过分析设计极及振动极变化,实现了三参数高阶系统的计算与分析[11]。本文研究PID控制,并结合传统陷波器[12-13]开展分析与设计,基于扩充参数平面法,并将PID控制参数整定和陷波器参数设计结合起来,综合考虑PID控制参数和陷波器参数对系统性能的影响。通过仿真分析,对比在PID位置控制中引入陷波器前后的抑制效果。结果显示:使用传统陷波器与PID控制能有效改善系统阻尼特性。

1 弹性系统数学模型

在交流伺服系统中,电机与负载之间常采用传动轴、滚珠丝杠副或者联轴器等传动机构进行连接。然而传动机构并不是理想刚性,电机和负载之间有弹性连接,弹性伺服系统常简化为二惯性系统来分析。

二惯性系统模型,如图1所示[14-15]。

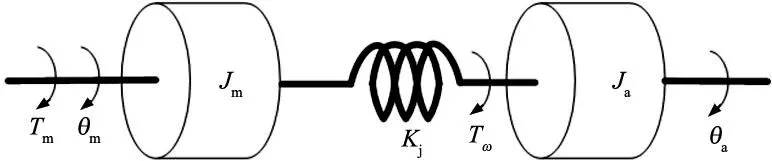
图1 二惯性系统模型

图1中,Jm为电机转动惯量(kg·m2);Ja为负载转动惯量(kg·m2);θm为电机旋转角度(rad);θa为负载旋转角度(rad);Kj为轴系弹性系数(N·m/rad);Tm为电机转矩(N·m);Tω为轴系转矩(N·m)。

二惯性系统框图如图2所示。

图2 二惯性系统框图

从图2系统框图可以得到电机转矩Tm到电机角度θm和负载角度θa的传递函数如下所示。

电机转矩Tm到电机角度θm的传递函数:

(1)

电机转矩Tm到负载角度θa的传递函数:

(2)

(3)

式中:ωa为反谐振频率,ω0为谐振频率,R为负载与电机的惯性比。

2 控制策略分析

2.1 PID控制系统

传统PID位置控制系统框图如图3所示[11]。

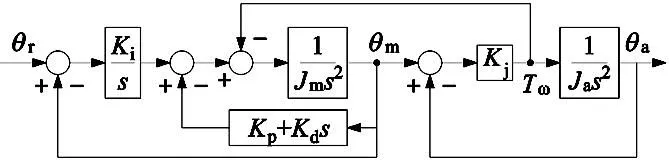
图3 PID位置控制系统框图

由图3可以得出从电机参考输入角度θr到电机角度θm和负载角度θa的传递函数:

(4)

(5)

式中:Kp为比例反馈系数,Ki为积分反馈系数,Kd为微分反馈系数,θr为参考输入角度。

2.2 基于扩充参数平面法的PID参数整定

式(5)位置控制系统由5个极点需要分配,但只有Kp、Ki、Kd三个控制参数,可调节参数远低于系统阶数少。使用扩充参数平面法,将系统分为3个设定极点和两个自由极点,具体步骤如下。

式(4)、式(5)分母,即系统的特征方程如下(m为系统阶数):

(6)

式中:ak为特征方程各阶系数。

设定极s1、s2设定为一组实部相同的共轭极点:

(7)

第三个设定极s3设定为沿s平面实轴放置:

s3=-ω2

(8)

式中:ω1、ω2为设计极频率,ζ1为阻尼系数。

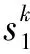
(9)

式中:函数Uk(ζ1)为第二类切比雪夫函数,此函数的参数ζ1的范围为:0≤|ζ1|≤1,此函数的递归式如下:

Uk+1(ζ1)-2ζ1Uk(ζ1)+Uk-1(ζ1)=0

(10)

设初始值U0(ζ1)≡0,U1(ζ1)≡1。

将式(9)代入式(6)中,为保证实部和虚部之和各为0,得到:

(11)

(12)

将式(8)代入式(6)可得:

(13)

式(11)～式(13)决定设定极点s1、s2、s3的位置,同时可以通过式(11)～式(13)确定控制参数Kp、Ki、Kd。

系统ak与Kp、Ki、Kd关系如下:

ak=bk+ckKp+dkKi+ekKd

(14)

式中:bk、ck、dk、ek是系统常数。

式(14)系数矩阵,结合式(4)和式(5)分母展开为:

(15)

从式(15)系数矩阵看出,控制参数Kp、Ki、Kd由电机转动惯量Jm、反谐振频率ωa和惯性比R决定。

展开式(14),综合式(11)～式(13)得到:

(16)

式中:

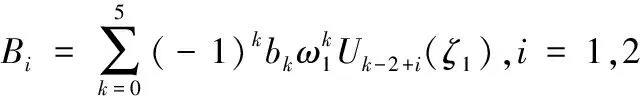
(17)

对式(16)求解,可以求解出控制参数Kp、Ki、Kd如下:

(18)

以上,通过ω1、ω2和ζ1来调整设计极点的位置;并根据式(18),通过求解方程组中系数得到对应的控制参数Kp、Ki、Kd。

3 系统分析

系统参数取传动轴扭转刚度Kj为5100 N·m/rad,取负载侧转动惯量Ja为0.488 3 kg·m2[16]。如下分析出惯性比和设定极点对系统振动的影响。

3.1 惯性比影响

设定极为非振动设计,选设定极s1、s2的阻尼系数ζ1=0.85,取ω1=0.5ωa;设定极s3与设定极s1、s2实部相等,即ω2=ω1ζ1,惯性比R取值为0.25,0.5,0.75,1,1.25时,自由极点位置如图4所示。

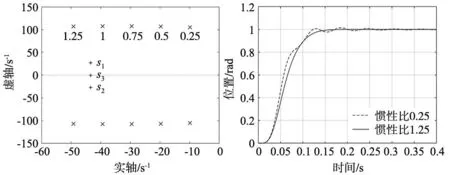
图4 不同惯性比极点位置图(R=0.25～1.25)

图4中符号(+)表示为s1、s2、s33个设定极点,符号(×)表示自由极点。从自由极点变化规律可以看出:当系统3个设定极点的位置固定时,随着系统惯性比增大,系统的两个自由极点逐渐远离虚轴。当系统的惯性比较小时,自由极点的位置靠近虚轴,此时系统处于欠阻尼状态。

惯性比R取值为0.25,1.25时,系统阶跃响应如图5所示。

通过图4和图5可以看出:惯性相对较小的系统更易呈现欠阻尼状态,此时系统的响应振动明显;惯性比相对较大,此时系统的响应较稳定。

3.2 设定极影响

针对小惯性比情况(R=0.25,0.5,0.75),改变设定极的位置(ω1=0.1ωa～0.9ωa),系统极位置如图6～图8所示。

图6 极点位置图(R=0.25)

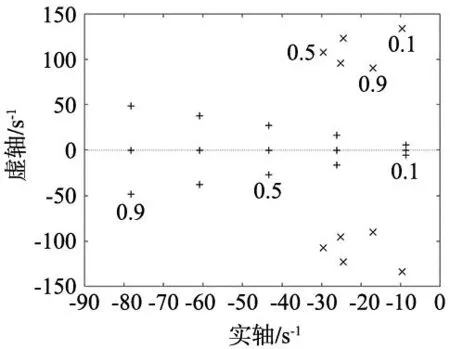
图8 极点位置图(R=0.75)

从图6～图8中可以看出,随着设定极(+)的取值ω1=0.1ωa～0.5ωa逐渐增大,设定极的位置逐渐远离虚轴,系统的自由极(×)也跟随设定极远离虚轴;但随着设计极取值ω1=0.5ωa～0.9ωa进一步增大,自由极返回虚轴,系统阻尼特性开始变差。

对比分析图6～图8可以看出:不同惯性比时,随着设定极的变化,系统自由极的运动规律相同;在小惯性比时,自由极均更靠近虚轴。因此,针对小惯性比系统欠阻尼特性,为了进一步提高系统的稳定性,在小惯性比系统中引入滤波器。

4 陷波器引入及设计分析

为了使其得到有效的抑制,直接的方法就是对特定谐振点的频率进行抑制[13]。加入陷波滤波器之后,谐振点峰值会被抑制,传统陷波器的传递函数表达式[7,12-13]:

(19)

式中:ε0为陷波器带宽参数。

陷波器带宽参数ε0=0.2,0.3,0.4时,陷波器Bode图如图9所示,随着陷波器带宽参数ε0变大,陷波器的陷波带宽变大。

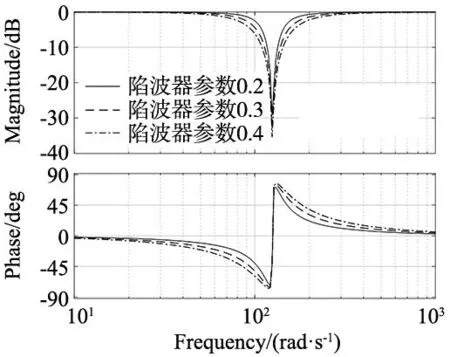
图9 陷波器Bode图(ε0=0.2,0.3,0.4)

在PID位置控制系统上,引入陷波器,使用扩充的参数平面法对控制参数进行整定,可以通过调节陷波器带宽参数ε0,分析出陷波器对系统性能的影响。

带陷波器PID控制系统框图如图10所示,从电机参考输入角度θr到电机角度θm和负载角度θa的传递函数:

(20)

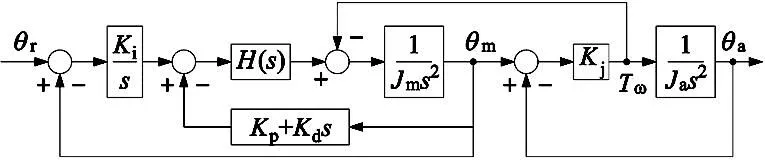
图10 带陷波器PID控制系统框图

(21)

系统引入传统陷波器后,系统的阶数仍为五阶系统,其系数矩阵为:

(22)

对比式(22)与式(15),引入陷波器后,式(22)多一个调节参数ε0。

通过扩充参数平面法对带陷波器的系统进行参数整定。基于上节分析,取小惯性比R=0.25,0.5、设定极点位置ω1=0.5ωa,改变陷波器带宽参数,调查极点位置及变化。

从图11和图12可以看出,引入陷波器后,通过改变陷波器带宽参数ε0,自由极点距离虚轴的距离和无陷波器系统相比明显变远,系统阻尼性能得到改善。

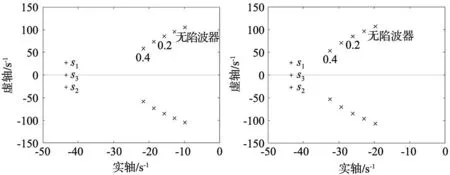
图11 极点位置图(R=0.25)

在惯性比0.25时,陷波器带宽参数ε0=0.4时,系统阶跃响应曲线如图13所示;在惯性比0.5时,ε0=0.3的阶跃响应曲线如图14所示。

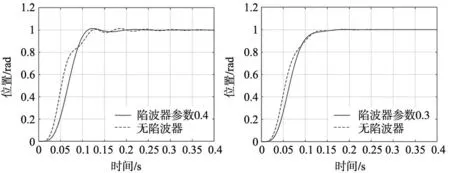
图13 阶跃响应曲线(R=0.25)

从图13和图14可以看出,惯性比R=0.25时,系统的振动明显,处于欠阻尼状态,所需陷波器带宽设计参数较大;惯性比R=0.5时,系统振动较小,陷波器带宽设计参数较小。通过对比引入滤波器前后系统的阶跃响应可知:引入滤波器后,系统的振动得到抑制。

5 结束语

针对弹性传动环节导致的伺服系统出现机械谐振的问题,本研究在谐振机理分析的基础上,综合系统PID控制与陷波器设计展开系统分析,揭示系统阻尼特征及陷波器的参数设计方法。

根据导出系统特征方程,基于扩充参数平面法分析PID设计,并总结出惯性比对系统阻尼特性的影响;针对小惯性比系统的欠阻尼特性情况,基于同方法,将PID控制参数整定和陷波器带宽参数调节结合设计,解决PID控制和陷波器带宽参数调节的优化设计,实现谐振抑制。