含多项式取绝对值函数的混沌系统分析与应用
高正中 杜翔


摘要: 为获得更复杂的动力学特性,设计了一种含有三次多项式取绝对值函数的混沌系统,该混沌系统的理论模型由含有3个状态变量的非线性方程组描述。分析了该系统的基本属性,以及相轨图、时域波形、Lyapunov指数、Poincaré映射、分岔图等动力学特性。系统在一定的参数条件下存在周期和混沌的特性,初值对称时存在共存吸引子或聚合吸引子。此外,某些系统参数变化时,系统存在恒定的动力学特性,状态变量初值变化时系统的动力学特性也是恒定的。电路仿真验证了理论的正确性。基于新设计的混沌系统设计了一种加密方案,对加密性能进行了分析,表明了加密方案的有效性。
关键词: 混沌;动力学;共存吸引子;共存分岔;图像加密
中图分类号: TP271.62 文献标识码: A
Analysis and Application of Chaotic System with Polynomial Absolute Valued Function
GAO Zhengzhong,DU Xiang
(College of Electrical Engineering and Automation, Shandong University of Science and Technology, Qingdao 266510, China)
Abstract:In order to get more complex dynamical properties, a chaotic system with cubic polynomial taking absolute value function is designed. The theoretical model of the chaotic system is described by a set of nonlinear equations with three state variables. The basic properties and the dynamic characteristics of the system like phase diagram, time domain waveform, Lyapunov exponent, Poincaré map and bifurcation diagram are analyzed. Under certain parameter conditions, the system has periodic and chaotic properties, and there are coexistence attractors or aggregation attractors when the initial values are symmetrical. In addition, when some system parameters change, the system has constant dynamic characteristics, when the initial value of the state variable changes, the dynamic characteristics of the system also remain unchanged. The correctness of the theory is verified by circuit simulation. Based on the newly designed chaotic system, an encryption scheme is designed, and the encryption performance is analyzed, which shows the effectiveness of the encryption scheme.
Keywords: chaos; dynamics; coexisting attractors; coexisting bifurcation; image encryption
0 引言
1963年,美国气象学家Lorenz在研究天气预报时,把大气动力学方程组进行简化并在计算机上进行模拟实验,发现舍去小数点后几位数字的模型与未舍去的模型迥然不同[1],于是他得出了“短期的天气预报可行,但长期不可行”的结论。Lorenz研究天气预报时提出了“蝴蝶效应”与混沌理论。这一理论表明确定性系统可以产生复杂的、类似随机的运动。自此,诸多学者纷纷开展了大量的研究。混沌理论已广泛应用于图像加密[24]、保密通信[57]和神经网络[810]等领域。师东生等[11]构建了一个在两个方向上具有四翼特征的五维超混沌系统。鲜永菊等[12]构造了一个四维超混沌系统,该系统有丰富的多稳态特性与多翼吸引子,最多有12种吸引子共存的情况。Yang等[13]从一个三维混沌系统出发,加入3个线性动态控制器得到了六维混沌系统,该系统有隐藏超混沌等复杂现象。Ma等[14]在三维自治混沌系统中加入平滑磁通控制的忆阻器和交叉项,设计了一种可以产生四翼混沌吸引子的新型四维超混沌系统。Qi等[15]从Lorenz系统出发,提出了一种每个状态方程都含有一个二次交叉项的新型混沌系统,该混沌系统有不动点、周期环、混沌等多種吸引子。Atiyeh等[16]提出了一个具有平衡面的四维混沌系统。Bao等[17]在亚遗传混沌Jerk电路里引入了一个忆阻器,得到了一个新型混沌电路,在系统状态变量初值不同时,系统有完全不同的动力学行为。Chen等[18]利用切换函数生成了环形、球形混沌吸引子。臧鸿雁等[19]给出了一个分段线性混沌映射,并分析了其与一个三次多项式映射拓扑共轭的充分条件。高秉建[20]通过增加第二类鞍焦平衡点的数目提出了一种新的生成多翼混沌吸引子的方法。
目前,含有多项式取绝对值的非线性函数并能产生共存吸引子且无忆阻器的混沌系统鲜有报道。不含有多稳态现象的混沌系统,动力学特性的复杂程度较低,实际应用时效果稍差,虽然忆阻系统可以产生共存吸引子,但忆阻器没有完全商用化,制备成本高,因此这样的混沌系统在物理实现时,成本自然很高。本文设计了一个表达式中含有三次多项式取绝对值的混沌系统,对系统进行了基本特性考察、动力学特性分析,发现系统存在共存吸引子或聚合吸引子,这降低了含共存吸引子的混沌系统的物理实现成本。并且进行了电路仿真,最后基于该系统设计了一种加密方案并验证了其有效性。
1 混沌系统描述
本文设计的混沌系统表达式:
其中,状态变量由x,y,z表示,系统参数由a,b,c,d,e,f,g表示。所有系统参数均大于0。
2 基本特性与动力学行为分析
2.1 系统相图、时域波形、Poincaré映射图
在系统状态方程中,若取a=4,b=5,c=4,d=0.1,e=1,f=1,g=7,并且系统初始条件设定为(x0,y0,z0)=(-1,-1,-1)时,系统产生的吸引子如图1所示。分析图1可知:系统的运动轨迹是杂乱无章的,同时可以发现吸引子具有涡卷结构,其吸引子属于混沌吸引子。
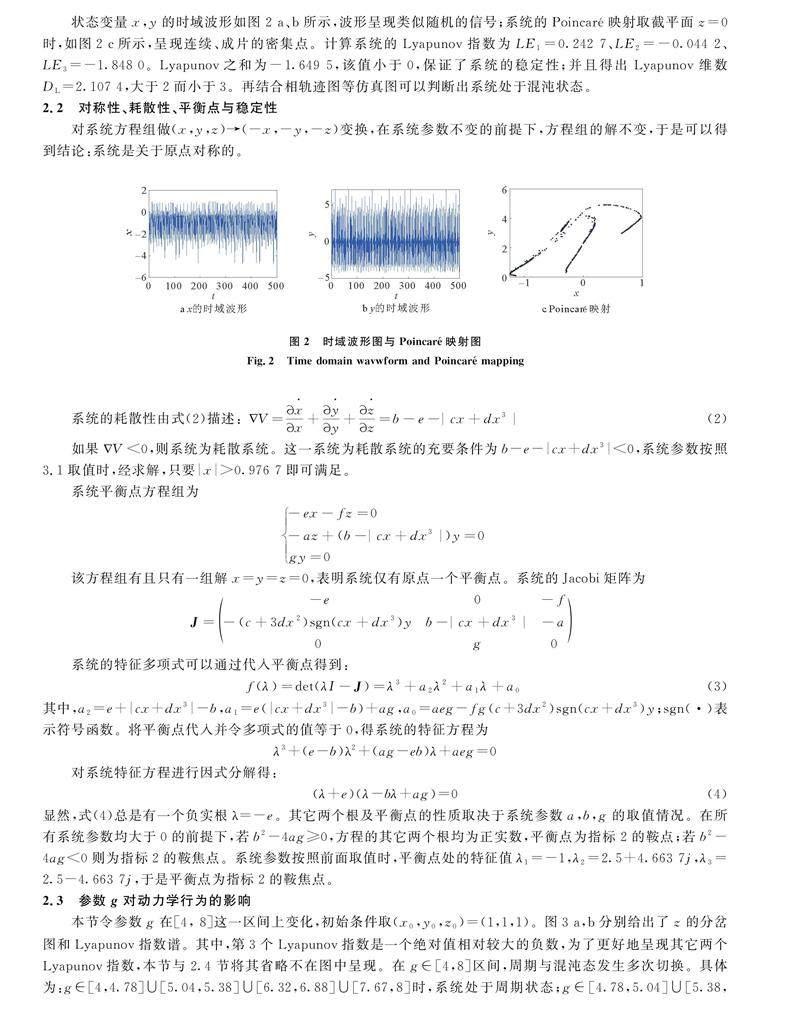
状态变量x,y的时域波形如图2 a、b所示,波形呈现类似随机的信号;系统的Poincaré映射取截平面z=0时,如图2 c所示,呈现连续、成片的密集点。计算系统的Lyapunov指数为LE1=0.242 7、LE2=-0.044 2、LE3=-1.848 0。Lyapunov之和为-1.649 5,该值小于0,保证了系统的稳定性;并且得出Lyapunov维数DL=2.107 4,大于2而小于3。再结合相轨迹图等仿真图可以判断出系统处于混沌状态。
2.2 对称性、耗散性、平衡点与稳定性
对系统方程组做(x,y,z)→(-x,-y,-z)变换,在系统参数不变的前提下,方程组的解不变,于是可以得到结论:系统是关于原点对称的。
显然,式(4)总是有一个负实根λ=-e。其它两个根及平衡点的性质取决于系統参数a,b,g的取值情况。在所有系统参数均大于0的前提下,若b2-4ag≥0,方程的其它两个根均为正实数,平衡点为指标2的鞍点;若b2-4ag<0则为指标2的鞍焦点。系统参数按照前面取值时,平衡点处的特征值λ1=-1,λ2=2.5+4.663 7j,λ3=2.5-4.663 7j,于是平衡点为指标2的鞍焦点。
2.3 参数g对动力学行为的影响
本节令参数g在[4, 8]这一区间上变化,初始条件取(x0,y0,z0)=(1,1,1)。图3 a,b分别给出了z的分岔图和Lyapunov指数谱。其中,第3个Lyapunov指数是一个绝对值相对较大的负数,为了更好地呈现其它两个Lyapunov指数,本节与2.4节将其省略不在图中呈现。在g∈[4,8]区间,周期与混沌态发生多次切换。具体为:g∈[4,4.78]∪[5.04,5.38]∪[6.32,6.88]∪[7.67,8]时,系统处于周期状态;g∈[4.78,5.04]∪[5.38,6.32]∪[6.88,7.67]时,系统处于混沌状态。
由图3b分岔图知,系统经历了多次正向、反向的分岔。其中,当g∈[5.38,6.32]时,分岔图显示了一些狭窄的周期窗口。选取不同的参数g,系统在x-z平面上的相图如图4所示。
2.4 参数f对动力学特性的影响
与2.3节类似,令参数f在[2,14]区间上变化,进行分析。首先,从图5a和b可以看出,首个Lyapunov指数一直大于0,第二根Lyapunov指数一直等于0,相图中则总是有成片的密集点,表明系统一直处于混沌态。然后,仅改变一个系统参数,令g=5.2,图5c和d重新给出了上述两幅仿真图,可以看出首个Lyapunov指数一直约等于0,第二根Lyapunov指数一直小于0,分岔图中点分布得比较稀疏,意味着系统一直处于周期态,因此系统参数f变化时,根据其它系统参数取值的情况,系统具有持续混沌或持续周期的特性。
2.5 参数变化时持续动力学特性理论分析
由2.3和2.4的分析知道,系统参数g变化能影响系统的动力学行为,而系统参数f变化不影响。将系统的平衡点代入特征方程,参数c,d,f会完全消去。具体来说,当x=y=z=0时,特征方程的系数a2=e-b,a1=ag-be,a0=aeg,即特征方程的系数与参数c,d,f无关。从理论上来讲,当这3个参数改变时,系统平衡点类型相同,拥有相同的动力学特性。
另外,由图5b,d知,当系统参数f改变时,分岔一直在下降,且分岔图或其上方轮廓类似反比例函数曲线,因此该系统参数改变时系统具有调幅特性。从理论上来说,系统参数c,d改变时,系统同样具有调幅特性[2122]。
2.6 状态变量初值对动力学行为的影响
本节中,令系统参数按照3.1取值,每次固定两个状态变量的初值等于1,第3个状态变量初值在[-30,30]之间变化,从图6所示的Lyapunov指数谱可以发现,3个状态变量初值在[-30,30]这一区间上变化时,Lyapunov指数谱符号总为(+,0,-),因此,在一定的参数条件下,系统初值变化时存在持续混沌的特性。
2.7 系统的共存吸引子与共存分岔
共存吸引子、共存分岔也是混沌系统的重要特征。共存吸引子是指系统参数取相同数值而初值不相等的时候,所产生的不一样的吸引子。其它系统参数按照3.1取值,改变g的数值,共存吸引子在x-y平面上的投影如图7a~e所示。其中,红色的轨迹为系统初值取(-1,-1,-2)时,系统的吸引子投影,蓝色的轨线则对应系统初值取(1,1,2)。x的共存分岔图如图7 f所示,红色的部分对应初值取(-1,-1,-2),蓝色对应系统初值取(1,1,2)。由图7各图可见,系统初值取对称值时,g∈[5.38,6.32]系统产生聚合混沌吸引子,g∈[4,5.38]∪[6.32,8]时产生对称共存吸引子。
3 系统的模拟电路仿真
模拟电路仿真通常在Multisim软件平台进行。首先,运算放大器的线性范围为±13.5V,模拟乘法器线性范围为±10V,因此需要对超过上述范围的状态变量z进行压缩变换。设z→2z,变换后,式(1)转化为
在电路的状态方程中,首先取电容C1=C2=C3= 10nF,R4=R5=R8=R10=R11=R12=R13=R15=R16=R17=R19 =10kΩ,对比系统方程和电路状态方程,得
1R1C1=1 000,1R2C1=2 000,1R3C2=8 000,1R6C2=5 000,1R18C2=4 000,1100R14C2=100,1R20C3=3 500
进而可求得R1=100kΩ,R2=50kΩ,R3=12.5kΩ,R6=20kΩ,R14=10kΩ,R18=25kΩ,R20=28.571kΩ。取R20=28.7kΩ,其它电路元件按照計算结果取值,令3个电容的初始电压均取-1V,即设定系统初值为(x0,y0,z0)=(-1,-1,-1),y-x平面、y-z平面的仿真实验结果如图9所示,证明了理论的正确性。
4 系统在图像加密中的应用
本加密解密算法基于新设计的混沌系统,结合了像素置乱和扩散的算法。像素置乱可以使得像素点偏离原始位置,使相邻像素相关程度下降;而扩散可以改变像素的灰度值,影响图像的统计特性。
本加密解密算法分为4部分——一个混沌密码发生器、两个明文无关的扩散算法和一个明文关联的置乱算法。加密解密过程如图10所示。
加密详细过程:
1)混沌密码发生器。借助新混沌系统生成6个M×N维的伪随机矩阵。记密钥为K={x0,y0,z0,r1,r2},具体步骤:
第1步:由输入密钥K的前3个值作为新混沌系统的初始值,共迭代r1+r2+MN次,其中前r1+r2次是为了跳过系统的暂态。得到的3个伪随机序列记作{xi}、{yi}、{zi},i=1,2,…,MN。
2)明文敏感性分析。该性能测试方法为:借助密钥K先后加密两幅图像P1和P2,其中P2从P1中随机选取一个像素点(i,j),将该像素点的值改变1得到。相应的密文图像分别记为C1和C2。计算C1和C2之间的NPCR(像素改变率)、UACI(归一化平均变化强度)值。上述方法共重复100次。最后计算上述2个指标的平均值。
仿真时,明文和密文图像分别选取2 000对相邻的像素点。由表1中的相关系数计算结果与图13的相邻像素灰度值示意图可得出结论:明文图像在各个方向都具有很强的相关性,而密文图像则无相关性。
3)密文敏感性分析。该性能测试方法与明文敏感性类似,不同在于,改变的不是明文图像的像素点,而是密文图像的像素点。并且需要用同一密钥对两个不同的密文图像解密分别得到P1和P2,计算P1和P2之间的NPCR、UACI值。对“Cameraman”加密后的图像,计算得NPCR=99.603 1%,UACI=31.173 9%,结果接近理论值,因此该加密方案具有较好的密文敏感性。
4)密钥灵敏度。正确的解密结果应如图14 a所示。但进行解密操作时若取密钥K={x0,y0,z0,r1,r2}={-1,-1,-1-10-15,35,201},解密结果将如图14 b所示。虽然密钥仅有一个数值有10-15的偏差,但直观上可以发现解密图像仍然呈现噪声形式,无法传达有效信息。这表明该加密方案的密钥灵敏度极优。
5 结论
本文设计了一种含有三次多项式取绝对值函数的混沌系统。通过数值分析和MATLAB仿真分析了基本属性和动力学特性。结果表明,虽然这一系统在一定的参数条件下仅有一个指标2的鞍焦平衡点,但存在混沌现象,且状态变量初值对称时存在共存吸引子或聚合吸引子。系统的某几个参数或系统初值变化时,具有持续周期或混沌的动力学特性,也有调幅特性。电路仿真验证了理论的正确性。最后基于新设计的混沌系统设计了加密方案,仿真与分析表明了加密方案的有效性。
参考文献:
[1]LORENZ E N. Deterministic non-periodic flows [J]. Journal of the Atmospheric Sciences, 1963, 20(3): 130-141.
[2]田兴华, 张纪会, 李阳. 基于混沌映射的自适应退火型粒子群算法 [J]. 复杂系统与复杂性科学, 2020, 17(1): 45-54.
TIAN X H, ZHANG J H, LI Y. An adaptive annealing particle swarm optimization based on chaotic mapping [J]. ComplexSystems and Complexity Science, 2020, 17(1): 45-54.
[3]LUO Y L, ZHOU R L, LIU J X, et al. A novel image encryption scheme based on Keplers third law and random Hadamard transform [J]. Chinese Physics B, 2017, 26(12): 120504.
[4]SUN J W, YANG Q F, WANG Y F. Dynamical analysis of novel memristor chaotic system and DNA encryption application [J]. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2020, 44: 449-460.
[5]刘林芳, 芮国胜, 张洋,等. 基于相空间对称Lorenz阵子群的混沌通信保密研究 [J]. 通信学报, 2019, 40(5): 32-38.
LIU L F, RUI G S, ZHANG Y, et al. Research on the chaotic secure communication of the phase-space symmetric Lorenz oscillator group [J]. Journal on Communications, 2019, 40(5): 32-38.
[6]SAHIN M, TASJIRAN Z, HASAN G, et al. Application and modeling of a novel 4D memristive chaotic system for communication systems[J]. Circuits, Systems, and Signal Processing, 2020, 39: 3320-3349.
[7]YU F, LIU L, HE B Y, et al. Analysis and FPGA Realization of a novel 5D hyperchaotic four-wing memristive system, active control synchronization, and secure communication application [DB/OL].[2022-02-02].http://doi.org/10.1155/2019/4047957.
[8]卢辉斌, 王丽佳. 基于Hopfield网络的彩色图像混沌加密算法 [J]. 吉林大学学报(信息科学版), 2014, 32(2): 131-137.
LU H B, WANG L J. Color image encryption algorithm of chaotic based on the hopfield network [J]. Journal of Jilin University (Information Science Edition), 2014, 32(2): 131-137.
[9]LIN H R, WANG C H, TAN Y M, et al. Hidden extreme multistability with hyperchaos and transient chaos in a Hopfield neural network affected by electromagnetic radiation [J]. Nonlinear Dynamics, 2020, 99: 2369-2386.
[10] 孙亮, 罗佳, 乔印虎.局部有源忆阻器电路及其在HR耦合神经元网络中的应用[J].电子与信息学报,2021,43(11): 3374-3383.
SUN L, LUO J, QIAO Y H. A Locally active memristor circuit and its application to a coupled hindmarsh-rose neuron network [J]. Journal of Electronics & Information Technology, 2021, 43(11): 3374-3383.
[11] 師东生, 石炜. 一个新四翼高维超混沌系统的复杂动力学行为研究与仿真 [J]. 现代电子技术, 2020, 43(19): 10-13.
SHI D S, SHI W. Research and simulation of complex dynamic behavior of new four-wing high-dimensional hyperchaotic system [J]. Modern Electronics Technique, 2020, 43(19): 10-13.
[12] 鲜永菊, 扶坤荣, 徐昌彪. 一个具有多翼吸引子的四维多稳态超混沌系统 [J]. 振动与冲击, 2020, 40(1): 15-22, 38.
XIAN Y J, FU K R, XU C B. A 4-D multi-stable hyper-chaotic system with multi-wing attractors [J]. Journal of Vibration and Shock, 2020, 40 (1): 15-22, 38.
[13] YANG L B, YANG Q G, CHEN G R. Hidden attractors, singularly degenerate heteroclinic orbits, multistability and physical realization of a new 6D hyperchaotic system [J]. Communications in Nonlinear Science and Numerical Simulation, 2020, 90: 105362.
[14] MA J, CHEN Z Q, WANG Z L, et al. A four-wing hyper-chaotic attractor generated from a 4-D memristive system with a line equilibrium [J]. Nonlinear Dynamics, 2015, 81: 1275-1288.
[15] QI G Y, CHEN G R, DU S Z, et al. Analysis of a new chaotic system [J]. Physica A, 2005, 352: 295-308.
[16] ATIYEH B, KARTHIKEYAN R, ABDUL J, et al. Dynamical analysis of a new multistable chaotic system with hidden attractor: antimonotonicity, coexisting multiple attractors, and offset boosting [J]. Physics Letters A, 2019, 383: 1450-1456.
[17] BAO H, WANG N, BAO B C, et al. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria [J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 57: 264-275.
[18] CHEN Q F, HONG Y G, CHEN G R. Chaotic behaviors and toroidal/spherical attractors generated by discontinuous dynamics[J]. Physica A, 2006, 371: 293-302.
[19] 臧鴻雁, 韦心元, 袁悦. 一类三次多项式混沌映射的判定及性能分析 [J]. 电子与信息学报, 2021, 43(2): 454-460.
ZANG H Y, WEI X Y, YUAN Y. Determination and properties analysis of a cubic polynomial chaotic map [J]. Journal of Electronics & Information Technology, 2021, 43(2): 454-460.
[20] 高秉建. 基于Liu混沌系统生成的多翅膀蝴蝶吸引子 [J]. 复杂系统与复杂性科学, 2016, 13(1): 91-94.
GAO B J. Multi-wing butterfly attractor from a modified chaotic system [J].Complex Systems and Complexity Science, 2016, 13(1): 91-94.
[21] WANG Z, SUN C, JIN F, et al. A widely amplitude-adjustable chaotic oscillator based on a physical model of HP memristor [J]. IEICE Electronics Express, 2018, 15(8): 1-6.
[22] WANG R, LI C B, CICEK S, et al. Amemristive hyperjerk chaotic system: amplitude control, FPGA design, and prediction with artificial neural network [DB/OL].[2022-02-01].http://doi.org/10.1155/2021/6636813.
(责任编辑 李 进)
收稿日期:2022-05-18;修回日期:2022-07-08
基金项目: 中国博士后科学基金(2015T80279);山东省自然科学基金(ZR2020MF071)
第一作者: 高正中(1971-),男,山东济宁人,博士,教授,主要研究方向为计算机检测与控制、机器人技术等。

