基于改进狼群算法优化LSTM网络的舆情演化预测

李若晨　肖人彬

摘要： 为提高预测舆情演化趋势的能力，提出了一种基于改进狼群算法（IWPA）优化长短期记忆（LSTM）神经网络的舆情演化预测模型。采用Halton Sequence进行初始化，提高种群多样性；设计步长因子进行高斯－正弦扰动变换，提高狼群探索开发能力；结合鲸鱼优化算法中的螺旋改进围攻机制，增强狼群的局部搜索能力；引入记忆力机制，使用双向记忆种群增加狼群协同合作能力，将改进后的狼群算法应用到LSTM神经网络的超参数预测。采用“新冠疫情”和“食品安全”等关键词作为实例，证明了IWPA-LSTM神经网络舆情演化预测模型具有良好的准确性和普适性，适用于多种舆情演化的预测。

关键词： 舆情演化预测；狼群算法；LSTM神经网络；Halton Sequence；正弦扰动；鲸鱼螺旋围攻机制；记忆力机制

中图分类号： TP18;TP183文献标识码： A

Public Opinion Evolution Prediction Based on LSTM Network Optimized by an Improved Wolf Pack Algorithm

LI Ruochen，XIAO Renbin

（School of Artificial Intelligence and Automation， Hua Zhong University of Science and Technology， Wuhan 430074， China）

Abstract：To improve the ability to predict the evolution trend of public opinion， a public opinion evolution trend prediction model based on an improved wolf pack algorithm and optimized long-short term memory neural network is proposed. Use Halton Sequence to initialization to improve population diversity. Design step factor to perform Gauss-Sine perturbation transformation to improve wolf group exploration and development capabilities. Combine with the spiral in the whale optimization algorithm to improve the siege mechanism to enhance the local search ability of wolves. The bidirectional memory population is used to increase the cooperative ability of the wolf pack. The improved wolf pack algorithm （IWPA） is applied to the hyperparameter prediction of the LSTM neural network. Using keywords such as “COVID－19” and “Food Safety”， the experiment proves that the IWPA-LSTM neural network public opinion evolution prediction model has good accuracy and generality. The model is suitable for the prediction of various public opinion evolution trends.

Keywords： public opinion evolution prediction; wolf pack algorithm; long short-term memory; Halton sequence; sine perturbation; whale spiral siege mechanism; memory mechanism

0 引言

近年来，随着社交媒体的快速发展，社交软件和网络平台都极大地促进了舆情的演化，研究新形势下的舆情演化情况，对于营造良好的网络环境至关重要［1］。在后疫情时代及时利用机器学习算法或深度学习算法挖掘疫情各种网络舆情信息，准确有效地预测网络舆情的走势，对社会具有重要意义［2］。

在挖掘自身历史数据进行趋势的分析和预测方面，很多学者对舆情的扩散演化过程进行了研究［3］。目前，舆情演化预测模型分为3种：自回归统计学模型、传统机器学习模型和深度学习模型。张和平［4］对百度指数舆论事件发展趋势的时序指标进行了几何平均模型修正预测。Anjaria M［5］将舆情数据进行主成分分析降维并用支持向量机模型（SVM）进行舆情预测。林玲等［6］使用改进灰狼算法优化的SVM模型采用百度指数进行舆情预测。由于舆情演化预测是一个复杂的多因素问题，传统模型具有局限性和主观性，SVM模型对核函數的选择敏感，大规模训练样本难以实施，越来越多的学者通过建立深度学习模型，利用神经网络算法来处理舆情演化。Ye［7］描述了基于反向传播神经网络（BPNN）的舆情趋势预测方法，并比较了遗传算法和模拟退火算法。孙靖超等［8］采用循环神经网络（RNN）来预测舆情的演化趋势，提出了自适应调节学习率的方法。傅丽芳［9］引入注意力机制改进LSTM神经网络，来预测和分析各种话题的热度。

舆情演化发展是多因素相互制衡的结果，表现出了复杂非线性的特点，并且舆情时序数据往往呈现时序关联和数据量大的特点，因此神经网络模型的应用优势凸显。递归神经网络RNN具有处理复杂数据、时间数据记忆效果等优点。特别是LSTM，是一种能有效解决数据间长时间依赖的专用RNN，可以通过中间层的信息来预测和分析舆论演变情况，然而LSTM网络模型为随机设置初始权值和参数，容易陷入局部最优解和具有较差的稳定性。魏腾飞［10］采用柯西变异策略改进的粒子群算法优化LSTM模型的参数，提高了预测准确率。于永进［11］利用鲸鱼算法来寻找LSTM模型中的参数，提高了绝缘纸的剩余寿命预测准确率。狼群算法（Wolf Pack Algorithm， WPA）［12］具有较高的寻优能力，由于狼群算法是一种随机概率搜索算法，能够以较大的概率快速找到最优解，具有并行性、较好的全局收敛性和计算鲁棒性。相比其他群智能算法，WPA尤其适合复杂函数求解。薛俊杰［13］将改进的狼群算法对多种典型测试函数进行仿真实验，并与多种智能算法进行对比分析，结果表明改进的狼群算法具有全局收敛性强、计算耗费低、寻优精度高等优势。叶勇［14］则利用狼群算法解决车辆动态分配问题，对比经典智能优化算法比较，表现更为良好。WPA处理复杂优化函數问题上优势明显。狼群算法现已成功地在故障预测［15］、交通信号配时［16］、模具组合分配［17］、PID控制［18］等多个智能领域上广泛应用，因此本文选择狼群算法改进LSTM神经网络的网络权值和初始参数。

针对以上研究存在的不足，为了解决舆情演化趋势预测问题，并提高舆情演化趋势的预测速度和预测精度，本文结合多种策略提出了一种改进的狼群算法（IWPA），并使用IWPA对LSTM神经网络的权重和初始参数进行优化，来解决LSTM神经网络参数寻优复杂的问题，提出一种具有更高准确性和普适性的舆情演化预测的新方法IWPA-LSTM，最终实现对各类舆情演化趋势的预测。

1 相关理论基础

1.1 LSTM神经网络

其中，Wo和bo分别为输出门的权重系数矩阵和偏置向量，ot为t时刻的输出门。

舆情演化分析数据为典型时序数据，LSTM模型增加了记忆单元，可以将信息进行长期筛选和保存，更加有效地应用于舆情演化分析中［21］。LSTM神经网络模型的训练结果需要制定合适的参数，通常这些参数是被事先给定的，不能够随着训练结果进行反馈调整，需要对参数进行组合优化。确定一组最适合的参数，可以有效提高LSTM神经网络的预测性能。由于狼群算法能够较好地解决非线性、多变量的优化问题，因此选择它来改进LSTM参数选择的缺陷。本文采用如图2的流程进行狼群算法优化LSTM神经网络模型。

1.2 狼群算法

标准狼群算法的标准和流程如下［2223］：

1）狼群初始化：假设狼群的猎物分布范围是一个N×D的欧几里得空间，其中N为狼群中狼的数量，D为变量数。初始狼群是在解空间内随机分布的，采用式（7）在D维解空间内随机分布N匹狼：

其中，第d维解空间的上界为xUd，对应着的下界为xLd；rand为（0，1）内的随机数。

根据目标函数值的大小来确定距离猎物的远近程度，狼群初始化后，选取适应度函数值最优的，记为Ylead。

2 改进狼群算法优化LSTM模型

2.1 改进狼群算法

狼群算法是一个新生的算法，其智能行为存在有待改进的地方，本文提出了一种改进狼群算法（Improved Wolf Pack Algorithm， IWPA），以便后续有效地应用于LSTM模型舆情演化分析中。

2.1.1 Halton Sequence初始化

原始的狼群算法采用随机初始化的方式来建立初始群体会导致算法的求解能力不够稳定。Halton Sequence常应用于随机生成均匀的空间点［24］。因此，本文利用Halton Sequence搜索算法对原始狼的位置进行初始化，从而使其在解空间内分配较为均匀，避免陷入局部最优解和重复运算。Halton Sequence搜索算法的原理为设定一个质数p为基数，以基数切分区间，形成不重复且均匀的初始种群分布位置。

设定实验中狼群种群数为50，解空间维度为二维，得到图3和图4。图3是在二维空间的随机位置分布图，可以发现图中存在位置点重合的现象，且存在部分位置空缺；图4是选取两个质数作为基数base1=2，base2=3的Halton Sequence分布图，图4中位置点均匀分散到解空间中，没有出现位置点重合的现象。

2.1.2 步长因子的高斯－正弦扰动变换

基础狼群算法在初始阶段迅速收敛，但是随着迭代数的增多，容易陷入局部最优值而停止，使整体收敛速度和优化精度下降。因此在迭代过程的前中期引入高斯函数可以增强算法的局部搜索能力；在迭代后期引入一个正弦步长因子扰动，有利于算法跳出局部最优解。步长因子的高斯－正弦扰动变换公式如式（17）：

其中，φ1、φ2、ω1、ω2和ρ2为常数系数，μ和σ2为高斯函数的均值和方差，ε为步长扰动比例。

为寻找合适满足理想衰减机制的高斯分布曲线和正弦扰动曲线，可以对核心参数进行仿真分析。仿真实验表明，当t在最大迭代次数为300，选定ε为0.3时，算法寻优效果最好，对应的步长因子变化曲线如图5所示。

2.1.3 基于鲸鱼算法的螺旋围攻行为

在狼群算法的猛狼围攻行为中，猛狼直接选择头狼位置向头狼逼近，虽然可以加快围攻行为，但是没有全面继续探索头狼周围的区域，使得狼群的搜索能力受限。为了给猛狼围攻行为加以导向，本文结合鲸鱼优化算法（Whale Optimization Algorithm， WOA）［25］中的螺旋式位置更新机制，在鲸鱼捕食行为中遇到目标猎物会吐泡泡组成网来攻击猎物，再通过螺旋搜索的围攻行为将猎物捕获，这种螺旋围攻机制可以防止猎物从一侧逃窜，应用到狼群算法中可以提高狼群局部探索能力，在头狼周围寻找更优解。加入WOA算法中的螺旋围攻机制后，猛狼的位置坐标更新如式（18）所示。

其中，α为对数螺旋常数，通常取值为1，随机数l∈［-1，1］，D′為当前第i只狼和头狼之间的距离，如式（19）所示。

为了加快狼群算法的围攻搜索速度，猛狼不仅通过螺旋围攻机制进行围攻行为，同时收缩包围范围，以Pc为概率向头狼位置进行围攻，获得优化后的猛狼围攻机制如式（20）所示。

构造目标函数为y=x21+x22，从图6中可以看出，当头狼位于hk时，采用螺旋围攻机制的猛狼xk可以以头狼为中心对周围的领域进行搜索，并且逐步逼近头狼位置，在搜索过程中就可以探索到更优于头狼位置的h*k，提高狼群发现最优解的能力。

2.1.4 基于Harmonic拥挤距离和记忆机制的种群更新策略

传统的狼群算法中仅仅用适应度最优的狼作为头狼，对于搜索过程中的记忆没有进行保存。同时，为了增加狼群之间的协同作用，基于记忆力机制提出构建记忆种群，包含正向记忆种群和反向记忆种群。利用Harmonic［26］平均距离公式取代了欧式距离，计算公式：

其中，max_rmd和min_rmd分别为正向记忆狼在d维上的最大值和最小值。

根据上述构建的正向记忆种群和反向记忆种群设置新的种群更新策略，设置动态记忆种群更新因子βm，记忆种群替换更新Rm只记忆狼，计算公式如式（24）、（25）所示。

其中，rand为（0，1）内的随机数，φ、ω和ρ为常数系数，t为迭代次数。

具体方法为：在每次迭代完成后，上一次迭代产生的正向、反向记忆种群按照Harmonic平均距离进行排序，若当前的头狼和正向记忆种群中Harmonic距离最大的狼相同，不引入记忆种群；若当前头狼和正向记忆种群中Harmonic距离最大的狼不同，根据正向记忆种群中Harmonic平均距离排序从大到小的前Rm只记忆狼，进行位置替换；在原始种群中随机更新Rm只狼，根据反向记忆种群中Harmonic平均距离排序从大到小的后Rm只记忆狼，进行位置更新；在每次种群更新后再更新正反向记忆种群。

2.2 改进狼群算法优化LSTM神经网络模型

LSTM神经网络模型的调参过程复杂，稳定性不足，会对预测结果产生较大的影响［29］。因此，可以结合IWPA算法确定一组较好的初始参数，即可以用头狼的位置作为最优解初始权值和参数。IWPA-LSTM神经网络算法流程图如图7所示，主要步骤为：

步骤1：进行数据清洗工作，并且将清洗好的舆情演化数据进行归一化处理，根据时间顺序将数据集划分成训练集和测试集。

步骤2：初始化LSTM神经网络所需参数和LSTM神经网络结构，包括两层LSTM隐含和一层dropout层。选取需要优化的模型的参数为［L1，L2，lr，batch］，分别代表两层隐含层神经元个数、学习率、批次大小［30］。

步骤3：初始化IWPA狼群算法参数，每只狼的位置代表着LSTM神经网络的权值和阈值，设置评价函数作为IWPA算法的目标函数，其中P代表划分出的训练集数量，yp和y′p代表经过训练集得到的真实值和预测值；Q代表划分出的测试集数量，yq和y′q代表测试集得到的真实值和预测值。

步骤4：根据初始种群建立正反向记忆种群，计算狼群的适应度值，根据适应度值Fitnesslead确定头狼。

步骤5：根据步长扰动策略更新探狼搜索和猛狼围攻行动，搜索解空间中的最优适应度值，且更新头狼。

步骤6：采用Harmonic拥挤距离和正反向记忆种群重新更新狼群位置坐标。

步骤7：当判断条件符合适应度函数的最大精度或超过最大迭代次数，则得到当前头狼坐标，作为LSTM网络的初始权值和参数，进行网络训练，否则转步骤4。

3 计算实验和案例验证

3.1 舆情演化数据来源

预测舆情演化趋势都是基于历史舆情演化值的时间序列来进行，历史舆情演化值是一种最为常用的预测来源指标［31］，舆情演化程度是一个单位时间内的增量信息［32］。在本文中选取最常用百度指数作为舆情演化程度的指标。所以本文采用python爬虫技术获取百度指数官网中对于关键词的百度指数趋势数据，设置“新冠疫情”、“食品安全”、“网络安全”、“收入分配”和“共同富裕”等关键词，按天获取到对应的百度指数作为实验数据。其中，爬取“新冠疫情”2021年2月3日到2022年4月14日共437组数据；爬取“食品安全”、“网络安全”、“收入分配”和“共同富裕”2021年11月14日到2022年4月13日各150组数据。

3.2 实验环境和数据指标

本实验采用AMD锐龙7－5800H芯片，8核心，8G内存，Windows 10操作系统，MATLAB2020b试验平台。采用均方根误差（RMSE）、平均绝对百分比误差（MAPE）作为评价标准，其公式如式（27），（28）所示。

3.3 单模型预测建模

“新冠疫情”是当今世界的重大公共卫生事件，预测公众的反映情况是十分必要的工作［33］。从图8可以看出，“新冠疫情”舆情演化中会存在平稳期和突发期，在平稳期中舆情演化指数波动较小，且呈现一定周期性；在突发期舆情演化指数波动较大，会出现峰值。为提高检验预测的效果，将舆情演化数据进行分类［34］。对于平稳期舆情演化预测数据，选取2021年2月3日到2021年7月3日共150组数据，其中30组为测试集，对2021年6月3日到2021年7月3日“新冠疫情”平稳类舆情演化趋势进行预测。对于突发期舆情演化预测数据，选取2021年10月31日到2022年3月30日共150组数据，其中30组为测试集，对2022年2月28日到2022年3月30日“新冠疫情”突发类舆情演化趋势进行预测。

为了测试LSTM模型在舆情演化预测应用上的性能状况，选取多种机器学习模型进行对比分析，包括BP神经网络模型、SVM支持向量机模型和LSTM模型［35］。其中BP神经网络和LSTM神经网络结构为7－50－50－1，学习率为0.001；SVM模型的惩罚因子C=2，核参数为10。单模型平稳期预测结果如图9和表1所示；单模型突发期结果如图10和表2所示。

采用上述3种预测模型，进行10次重复实验取平均值。从表1和表2可以看出，3种模型在平稳期的表现都好于突发期，但是LSTM模型的表现是三者中最优的。

图9为平稳类舆情演化预测情况：LSTM模型的预测曲线更为贴合真实值。图10为突发类舆情演化预测情况：BP神经网络模型可能出现滞后性，而SVM模型和LSTM模型的MAPE误差相近，但LSTM神经网络模型的RMSE明显优于SVM模型，为4.946 6×103，说明LSTM模型对于这两类舆情演化数据的预测精度更高，更符合舆情演化的实际情况，对于平稳类舆情演化的情况适用性更好，同时也可以更准确地预测突发类舆情演化情况。

3.4 基于改进狼群算法的LSTM模型

根据单模型LSTM的结构，选择LSTM中的超参数进行不同智能算法的寻优，设定隐藏层单元个数的范围L1，L2∈［12，200］，学习率的范围lr∈［0.001，0.05］，batchsize∈［8，256］。为了测试改进后的狼群算法对于LSTM模型的优化性能，选取了原始LSTM模型（记作LSTM）、PSO优化的LSTM模型（记作PSO-LSTM）、WPA优化的LSTM模型（记作WPA-LSTM）和IWPA优化的LSTM模型（记作IWPA-LSTM）分别对“新冠肺炎”平稳期舆情演化趋势进行预测，将得到的实验结果比对。以上不同的改进算法的迭代次数为100，种群规模为30，3种不同的智能算法对LSTM超参数寻优过程如图11所示。

从图11中可以看出，IWPA算法相较于以上两种算法，因为引入了记忆种群，所以寻优次数要明显少于PSO算法和WPA算法，得到的适应度函数值是三者中最小的，说明IWPA算法对处理LSTM模型预测舆情演化是有效性的。最终，使用IWPA算法优化得到的LSTM超参数值为：隐藏层神经元个数分别为L1=83、L2=109，学习率lr=1.219×10-3，batch=36。不同模型平稳期预测结果见图12和表3；不同模型突发期结果如图13和表4所示。

采用上述3种不同算法优化的LSTM模型取平均值，得到预测舆情演化趋势图和预测误差表。平稳期IWPA-LSTM对比其余3个LSTM模型MAPE指标都有明显降低，说明IWPA-LSTM模型具有较高的精确性。突发期IWPA-LSTM模型的RMSE指标为4.946 6×103，小于其他3种模型的RMSE指标，这说明IWPA算法对于增加LSTM模型的稳定性具有重要作用；IWPA-LSTM模型的MAPE指标为6.5%，小于其余3个LSTM模型，这说明IWPA算法对于LSTM神经网络模型可以有效地提升收敛速度和提高预测精度。

综合以上分析，IWPA算法对于LSTM的優化效果明显，并且对两类舆情演化时期都有促进作用，在平稳期可以增加预测的精度，在突发期可以提高稳定预测的能力，可以发现IWPA-LSTM模型对于预测舆情演化趋势都具有稳定性好、精确度高的特点，证明使用改进狼群算法优化LSTM具有更为良好的预测性能。

根据数据分析，在2021年6月到7月，国内疫情防控较为稳定，随着“广州首例阿婆出院”广州各地风险逐渐解除，全国各地正常生产生活，舆情演化趋势也逐渐下降。从2022年2月28日“新冠疫情”舆情演化的趋势呈现上升现象，直到3月10日后，某学院学生发文称学院对于疫情的管理不当，引发人们对新冠疫情关注程度突然增高；3月10日到15日各地各部门采取相关有效措施，各省份对疫情地区进行点对点支援，舆情指数关注趋势在3月15日之后有所下降，证明了及时采取相关措施，可以有效缓解舆情演化趋势进一步提升。根据以上实际情况的分析，可以看出IWPA-LSTM神经网络对于社会舆情的实际意义明显，可以有效准确地预测舆情演化趋势，对于分析舆情演化原因可以提供有力的支持。

3.5 IWPA-LSTM模型泛化性验证

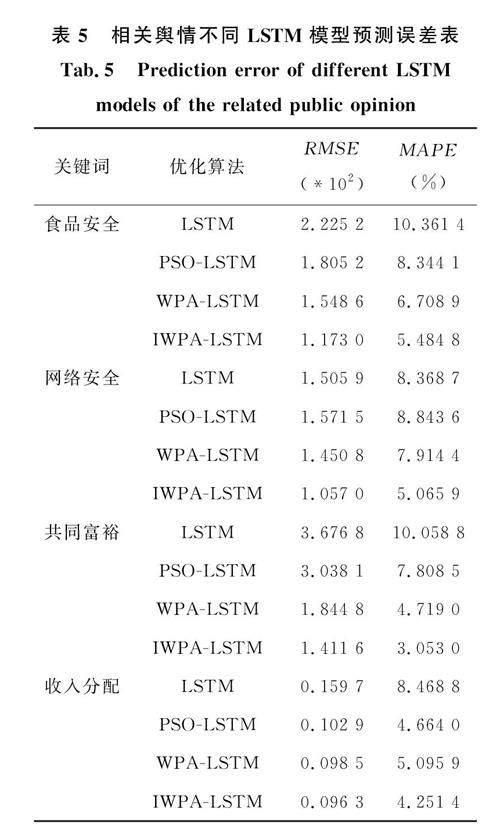
为了进一步验证狼群算法改进后的LSTM神经网络模型具有预测舆情演化趋势的泛化性，可以适用于其他多种舆情关键词的趋势预测，采用其他舆情进行验证。315晚会后，以“食品安全”和“网络安全”为关键词进行舆情演化预测，同时从2022年新华网发布的两会热词选取了“收入分配”和“共同富裕”。选择2021年11月14日到2022年4月13日共150组数据，其中34组为测试集。同时采用本文提到的LSTM、PSO-LSTM、WPA-LSTM和IWPA-LSTM 4种模型进行对比训练和预测，得到实验结果如图14和表5所示。

从图14和表5，分析“食品安全”舆情预测结果，IWPA-LSTM模型的MAPE指标最小为5.48%，并且RMSE指标为1.173 0×103，也是4种模型中最稳定的，因为“315晚会”后曝光了食品相关事件，造成在3月15日后舆情演化呈一定的上升趋势。对于其他3个相关舆情的预测，使用IWPA-LSTM模型的效果最好，在4种LSTM模型中，MAPE指标和RMSE指标均为最小，并且舆情演化趋势最为贴近实际情况。通过以上多个实例进行验证，使用IWPA算法优化的LSTM神经网络能够更好地适用于预测舆情演化趋势，对比其他算法优化的LSTM模型，具有较好的普适性和准确性，表现出了对不同舆情信息的良好适应性。

4 总结与展望

舆情的演化趋势具有实时性、无规律性，为了解决舆情演化趋势的预测问题，本文提出了一种改进狼群算法优化的长短期记忆神经网络预测模型（IWPA-LSTM），在经典狼群算法中引入初始化策略、动态高斯－正弦扰动步长策略、鲸鱼螺旋围攻策略，并建立正反双向记忆种群，提出改进狼群算法IWPA。LSTM神经网络模型可以较好地处理不同时期的“新冠疫情”舆情演化数据，采用IWPA优化LSTM神经网络对超参数进行寻优，可以避免人工调参的不确定性，提高预测的准确程度。IWPA-LSTM舆情演化预测模型应用于其他相关舆情的预测时，对比其他算法优化的LSTM神经网络模型表现出了良好的预测精度和普适性。

未来可以进一步探索舆情演化的相关因素，结合大数据处理方式，扩大预测范围，融合多种群多模型对舆情发展趋势进行更为精确的探索。

参考文献：

［1］于同洋， 肖人彬， 侯俊东. 网络舆情结构逆转建模与仿真：基于改进Deffuant模型［J］. 复杂系统与复杂性科学， 2019， 16（3）： 30－39.

YU T Y， XIAO R B， HOU J D. Modeling and simulation of network public opinion structure reversal： based on an improved Deffuant model［J］. Complex Systems and Complexity Science， 2019， 16 （3）： 30－39.

［2］张轩宇， 陈曦， 肖人彬. 后真相时代基于敌意媒体效应的观点演化建模与仿真［J］. 复杂系统与复杂性科学， 2023， 20（3）： 44－51，59.

ZHANG X Y， CHEN X， XIAO R B. Modeling and simulation of viewpoint evolution based on hostile media effect in the post truth era ［J］. Complex Systems and Complexity Science， 2023， 20（3）： 44－51，59.

［3］刘举胜， 何建佳， 韩景倜， 等. 观点動力学研究现状及进展述评［J］. 复杂系统与复杂性科学， 2021， 18（2）： 9－20.

LIU J S， HE J J， HAM J T， et al. Review on the research status and progress of viewpoint dynamics［J］. Complex Systems and Complexity Science， 2021， 18 （2）： 9－20

［4］张和平， 陈齐海. 基于灰色马尔可夫模型的网络舆情预测研究［J］. 情报科学， 2018， 36（1）： 75－79.

ZHANG H P， CHEN Q H. Research on internet public opinion prediction based on grey Markov model ［J］. Information Science， 2018， 36（1）： 75－79.

［5］Anjaria M， Guddeti R. Influence factor-based opinion mining of twitter data using supervised learning［C］//2014 Sixth International Conference on Communication Systems and Networks （COMSNETS）. Bangalore， India： IEEE， 2014.

［6］林玲， 陈福集， 谢加良， 等. 基于改进灰狼优化支持向量回归的网络舆情预测［J］. 系统工程理论与实践， 2022，42（2）： 487－498.

LIN L， CHEN F J， XIE J L，et al. Network public opinion prediction based on improved grey wolf optimization support vector regression［J］. Systems Engineering Theory and Practice， 2022， 42（2）： 487－498.

［7］野雪莲， 杨孔雨. 舆情趋势预测中神经网络的优化算法［J］. 网络新媒体技术， 2016， 5（1）： 33－37，51.

YE X L，YANG K Y. Neural network optimization algorithm in public opinion trends prediction［J］. Journal of Network New Media， 2016， 5（1）： 33－37，51.

［8］孙靖超， 周睿， 李培岳， 等. 基于循环神经网络的网络舆情趋势预测研究［J］. 情报科学， 2018， 36（8）：118－122，127.

SUN J C， ZHOU R， LI P Y，et al. Research on network public opinion trend prediction based on recurrent neural network［J］. Information Science， 2018， 36（8）： 118－122，127.

［9］傅丽芳， 赵菲菲. 基于注意力机制LSTM模型的农业舆情预测与分析［J］. 数学的实践与认识， 2021， 51（17）： 64－76.

FU L F， ZHAO F F. A forecasting method of agricultural public opinion based on Lda-Lstm-Attn model［J］. Journal of Mathematics in Practice and Theory， 2021， 51（17）： 64－76.

［10］ 魏腾飞， 潘庭龙. 基于改进PSO优化LSTM网络的短期电力负荷预测［J］. 系统仿真学报， 2021， 33（8）： 1866－1874.

WEI T F， PAN T L.Short-term power load forecasting based on LSTM neural network optimized by improved PSO［J］. Journal of System Simulation， 2021， 33（8）： 1866-1874.

［11］ 于永进， 姜雅男， 李长云. 基于WOA-LSTM模型的机－热老化绝缘纸剩余寿命预测方法［J］. 电工技术学报， 2022， 37（12）： 3162－3171.

YU Y J， JIANG Y N， LI C Y.Prediction method of insulation paper remaining life with mechanical-thermal synergy based on whale optimization algorithm-Long-Short Term Memory model［J］. Transactions of China Electrotechnical Society， 2022， 37（12）：3162－3171.

［12］ 吳虎胜， 张凤鸣， 吴庐山. 一种新的群体智能算法——狼群算法［J］. 系统工程与电子技术， 2013， 35（11）： 2430－2438.

WU H S， ZHANG F M， WU L S. A new swarm intelligence algorithm—wolf packalgorithm［J］. Systems Engineering and Electronics， 2013， 35（11）： 2430－2438.

［13］ 薛俊杰， 王瑛， 李浩， 等. 一种狼群智能算法及收敛性分析［J］. 控制与决策， 2016， 31（12）：2131－2139.

XUE JJ， WANG Y， LI H， et al. A smart wolf pack algorithm and its convergence analysis［J］. Control and Decision， 2016， 31 （12）： 2131－2139.

［14］ 叶勇， 张惠珍. 多配送中心车辆路径问题的狼群算法［J］. 计算机应用研究， 2017，34（9）：36－39.

YE Y， ZHANG H Z.Wolf pack algorithm for multi-depot vehicle routing problem［J］. Application Research of Computers， 2017，34（9）： 36－39.

［15］ 尹怀仙， 王凯， 张铁柱， 等. 基于PSO-BP神经网络的城轨列车转向架轮对轴箱故障预测［J］. 复杂系统与复杂性科学， 2015， 12（4）： 97－103.

YIN H X， WANG K， ZHANG T Z，et al. Fault prediction based on PSO-BP neural network about wheel and axle box of bogie in urban rail train［J］. Complex Systems and Complexity Science， 2015， 12（4）： 97－103

［16］ 胡亮， 肖人彬， 王英聪. 蜂群激发抑制算法及其在交通信号配时中的应用［J］. 复杂系统与复杂性科学， 2019， 16（2）： 9－18，40.

HU L， XIAO R B， WANG Y C.Bee colony activating-inhibition algorithm and its application in traffic signal timing［J］. Complex Systems and Complexity Science， 2019， 16（2）： 9－18，40.

［17］ 韩忠华， 刘约翰， 李曼， 等. 改进狼群算法求解模具在模台上组合分配问题［J］. 系统仿真学报， 2021， 33（1）： 127－140.

HAN Z H， LIU Y H， LI M， SUN LL， et al. Improved wolf pack algorithm for distribution of molds on molds table［J］. Journal of System Simulation， 2021， 33（1）： 127－140.

［18］ WU H S， ZHANG F M. A uncultivated wolf pack algorithm for high-dimensional functions and its application in parameters optimization of PID controller［C］//2014 IEEE Congress on Evolutionary Computation （CEC）. Beijing， China： IEEE， 2014.

［19］ 刘东阳， 查文文， 陶亮， 等. 基于LSTM和SMC的农用履带机器人轨迹跟踪控制［J］. 系统仿真学报， 2023， 35（4）： 747－759.

LIU D Y， ZHA WW， TAO L， et al. Trajectory control of crawler robot based on LSTM and SMC ［J］. Journal of System Simulation， 2023， 35（4）： 747－759.

［20］ EOM G， BYEON H. Development of keyword trend prediction models for obesity before and after the Covid-19 pandemic using RNN and LSTM： analyzing the news big data of South Korea［J］. Frontiers in Public Health， 2022， 10： 894266.

［21］ DU B G， HUANG S， GUO J， et al. Interval forecasting for urban water demand usingPSO optimized KDE distribution and LSTM neural networks［J］. Applied Soft Computing， 2022， 122： 108875.

［22］ 陈暄， 孟凡光， 吴吉义. 求解大规模优化问题的改进狼群算法［J］. 系统工程理论与实践， 2021， 41（3）： 790－808.

CHEN X， MENG F G， WU J Y.Improved wolf pack algorithm for large－scale optimization problems［J］. Systems Engineering Theory and Practice， 2021， 41（3）： 790－808.

［23］ GAO Y J， ZHANG F M， ZHAO Y， et al. Quantum-inspired wolf pack algorithm to solve the 0-1 knapsack problem［J］. Mathematical Problems in Engineering， 2018（4）： 5327056.

［24］ 刘成汉， 何庆. 融合多策略的黄金正弦黑猩猩优化算法［J］. 自动化学报， 2023， 49（11）： 2360－2373.

LIU C H， HE Q.Golden sine chimp optimization algorithm integrating multiple strategies［J］. Acta Automatica Sinica， 2023， 49（11）： 2360－2373.

［25］ MIRJALILI S， LEWIS A. The whale optimization algorithm［J］. Advances in Engineering Software， 2016， 95： 51－67.

［26］ 罗辞勇， 陈民铀， 张聪誉. 采用循环拥挤排序策略的改进NSGA-Ⅱ算法［J］. 控制与决策， 2010， 25（2）： 227－231.

LUO C Y， CHEN M Y， ZHANG C Y.Improved NSGA-Ⅱ algorithm with circular crowded sorting［J］. Control and Decision， 2010， 25（2）： 227－231.

［27］ 王艳娇， 马春蕾. 基于记忆策略的动态离子运动优化算法［J］. 吉林大学学报（工学版）， 2020， 50（3）： 1047－1060.

WANG Y J， MA C L.Dynamic ion motion optimization algorithm based on memory strategy［J］. Journal of Jilin University （Engineering and Technology Edition）， 2020， 50（3）： 1047－1060.

［28］ 汪慎文， 丁立新， 谢承旺， 等. 应用精英反向学习策略的混合差分演化算法［J］. 武汉大学学报（理学版）， 2013， 59（2）： 111－116.

WANG S W， DING L X， XIE C W， et al. A hybrid differential evolution with elite opposition-based learning［J］. Journal of Wuhan University （Natural Science Edition）， 2013， 59（2）： 111－116.

［29］ HUANG Z H， WEI X， KAI Y. Bidirectional LSTM-CRF models for sequencetagging［DB/OL］. ［2022－01－30］. https：//doi.org/10.48550/arXiv.1508.01991

［30］ 王鑫， 吳际， 刘超， 等. 基于LSTM循环神经网络的故障时间序列预测［J］. 北京航空航天大学学报， 2018， 44（4）： 772－784.

WANG X， WU J， LIU C， et al.Exploring LSTM-based recurrent neural network for failure time series prediction［J］. Journal of Beijing University of Aeronautics and Astronautics， 2018， 44（4）： 772－784.

［31］ XIAO R B， YU T Y， HOU J D. Modeling and simulation of opinion natural reversal dynamics with opinion leader based on HK bounded confidence model［J］. Complexity， 2020（1）： 7360302.

［32］ 刘琪， 肖人彬. 观点动力学视角下基于意见领袖的网络舆情反转研究［J］. 复杂系统与复杂性科学， 2019， 16（1）： 1－13.

LIU Q， XIAO R B. An opinion dynamics approach to public opinion reversion with the guidance of opinion leaders［J］. Complex Systems and Complexity Science， 2019， 16（1）： 1－13.

［33］ 刘巧玲， 李劲， 肖人彬. 基于参数反演的网络舆情传播趋势预测——以新浪微博为例［J］. 计算机应用， 2017， 37（5）： 1419－1423.

Liu Q L， Li J， Xiao R B.Trend prediction of public opinion propagation based on parameter inversion—an empirical study on Sina micro-blog ［J］. Journal of Computer Applications， 2017， 37（5）： 1419－1423.

［34］ WU H S， XIAO R B.Flexible wolf pack algorithm for dynamic multidimensional knapsack problems［J］. Research， 2020（1）： 174－186.

［35］ LI J H， ZHU D S， LI C X. Comparative analysis of BPNN， SVR， LSTM， Random Forest， and LSTM-SVR for conditional simulation of non-Gaussian measured fluctuating wind pressures［J］. Mechanical Systems & Signal Processing， 2022， 178： 109285.

（责任编辑 耿金花）

收稿日期： 2022－05－25；修回日期： 2022－06－30

基金项目： 科技创新 2030—“新一代人工智能”重大项目（2018AAA0101200）

第一作者： 李若晨（1998－），女，山东淄博人，硕士，主要研究方向为舆情预测、群智能。

通信作者： 肖人彬（1965－），男，湖北武汉人，博士，教授，主要研究方向为复杂系统、群智能。