煤矿井下掘进机器人路径规划方法研究
张旭辉,郑西利,杨文娟,*,李语阳,麻 兵,董 征,陈 鑫
(1.西安科技大学 机械工程学院,陕西 西安 710054;2.陕西省矿山机电装备智能监测重点实验室,陕西 西安 710054)
目前,煤矿机器人的研究还存在诸多难题,特别是煤矿掘进机器人受巷道特殊的非结构化环境及复杂工艺流程制约,自主化、智能化水平相对较低[1-3]。在非全断面巷道作业时,主要依靠人工操作将掘进机器人移机进行二次截割以完成断面成形任务,但由于井下环境恶劣,人工移机操作难度大、效率低下,并且存在较大的安全隐患。因此,研究掘进机器人的自主移机是实现煤矿无人化开采的重要一环[4-6],而非全断面巷道作业条件下的掘进机器人路径规划是实现自主移机的前提,同时对提高掘进工作面智能化水平、掘进作业效率及巷道断面成形质量均具有重要意义。
煤矿掘进机器人是一种特殊的履带式机器人[7-8],其工作环境为狭长巷道,作业时极易发生碰撞,因此研究掘进机器人与巷道侧壁的碰撞检测,对机器人规划一条安全、无碰撞的可行路径具有重要意义[9]。针对机器人碰撞检测问题,国内外学者进行了大量研究。碰撞检测主要关注在二维或三维环境中,确定两个或多个物体在运动过程中是否相互接触或相交。常见的三维碰撞检测方法主要有图像空间法[10-11]、空间剖分法[12-13]和层次包围盒法[14-15]。图像空间法可以将三维模型在预设的二维平面上进行投影,再基于二维空间中图像采样及对应深度信息判断三维模型相交情况,该方法受限于图像分辨率,检测结果不够精确。空间剖分法主要是利用某种规则把空间分割成若干个子空间,然后在子空间内对碰撞检测进行单独处理,同时采用降低子空间内无关对象相交测试的方法来缩短碰撞检测所需的时间,该方法可在一定程度上处理多设备间的碰撞检测,但在处理形体过大或复杂物体的碰撞检测时具有局限性。层次包围盒法通过将被检测对象的包围盒进行层次化组织,形成一个树结构,从而实现更加快速和准确的碰撞检测,该方法在机器人碰撞检测方面应用广泛。
针对掘进机器人路径规划问题,众多学者进行了深入研究。在机器人路径规划方面,常见的方法主要有4 类:人工势场和模糊逻辑法等传统方法[16-17]、A*算法和栅格法等图形学方法[18-20]、蚁群算法和粒子群优化算法等智能仿生学方法[21-23]以及策略梯度法和模仿学习法等强化学习方法[24-25]。基于传统方法的路径规划描述简单易于实现,但容易陷入局部最优解。基于图形学方法的路径规划可提供建模方法,但大多将机器人以质点处理,且搜索效率低下。基于智能仿生学方法的路径规划具有仿生学特点,更加智能高效,但收敛速度较慢。以上研究集中在移动机器人的避障路径规划,研究对象以小型移动机器人为主,在掘进机器人机身路径规划方面研究较少。由于煤矿巷道成形精度取决于截割轨迹,对掘进机器人机身路径规划和截割臂控制精度提出更高的要求。为保证狭长巷道中掘进机器人路径的可行性,须考虑掘进机器人自身大小,从而得到合理的规划路径。
因此,通过对虚拟环境碰撞检测、智能体全局路径规划等内容展开研究,提出一种基于深度强化学习的掘进机器人机身路径规划方法,在井下非结构化环境条件下为机器人规划安全可行路径。首先,利用深度相机构建三维巷道模型,采用包围盒技术实现掘进机器人运动模型与三维巷道模型之间的碰撞检测,形成掘进机器人路径规划过程中的边界避障策略。其次,基于奖惩机制构建智能体,并采用深度强化学习技术对其进行训练,完成掘进机器人机身路径规划。最后,搭建掘进机器人路径规划实验平台,对所提方法进行验证。以实现煤矿井下非全断面作业条件下的掘进机器人自主移机路径规划,为井下掘进机设备的智能化和自动化奠定基础。
1 掘进机器人路径规划总体方案
巷道断面成形作业时机身移动多为人工操控,导致掘进效率低下、安全性差。解决非全断面巷道作业掘进机器人自主移机难题,需要实现对掘进机器人工况环境的实时监测、掘进机器人与掘进工作面间的碰撞检测以及掘进机器人运动路径的自主规划。
因此,在掘进机器人机身上布置多源传感器实现掘进工作面环境实时监测,在虚拟环境中构建掘进机器人与工作面间的碰撞检测模型,生成巷道边界受限条件下的避障策略,再利用深度强化学习方法训练智能体得到掘进机器人全局路径,并采用虚实结合的方式实现虚实空间中掘进机器人运动路径同步规划。
掘进工作面环境以狭长直行巷道为主,且针对掘进机器人巷道施工时左右移机路径规划问题,提出的路径规划总体方案如图1 所示,包括传感检测单元、碰撞检测单元和路径规划单元。
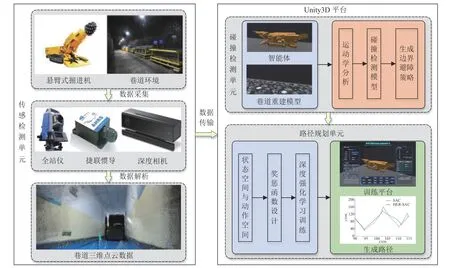
图1 掘进机器人路径规划总体方案Fig.1 Overall scheme for path planning of cantilever roadheader robot
该方案中,传感检测单元通过多源传感器采集掘进机器人位姿数据,深度相机扫描得到巷道环境三维点云数据并实时传输至Unity3D 平台中实例化,实现虚拟环境巷道实时重建;构建掘进机器人运动学模型,进行运动学分析。碰撞检测单元根据巷道重建模型建立掘进机器人与巷道侧壁间的碰撞检测模型,并使用层次包围盒法进行虚拟环境碰撞检测,形成巷道边界受限下的避障策略。路径规划单元基于掘进机器人运动特性定义其状态空间与动作空间,根据奖惩机制将掘进机器人模型作为智能体,进行奖惩函数设计,再结合边界避障策略采用深度强化学习技术对智能体进行训练,实现非全断面巷道作业条件下的掘进机器人路径规划。
2 巷道边界受限下的避障策略
掘进机器人在非全断面巷道作业条件下的移机过程,存在转弯和直行两种运动方式,在狭长巷道中,掘进机器人的转弯过程极易与巷道侧壁发生碰撞。因此,需要对掘进机器人进行运动学分析,并建立虚拟碰撞检测模型,采用层次包围盒算法实现掘进机器人边界避障功能。
2.1 掘进机器人运动学分析
掘进机器人的转弯过程是通过左右轮履带差速驱动完成的。若掘进机器人运动过程中,左右轮履带和地面无横向滑移,且履带转动速度地面平行时,可以将机器人的运动过程看作是二维运动学求解[26]。
掘进机器人运动学模型如图2 所示,建立巷道平面坐标系XOY,以掘进机器人的机身质心O0为原点,建立掘进机器人坐标系X0O0Y0,其中O0Y0轴平行于掘进机器人本体中心线,以朝向截割头方向为正方向,O0X0轴垂直于O0Y0轴,以指向掘进机器人右侧方向为正方向。
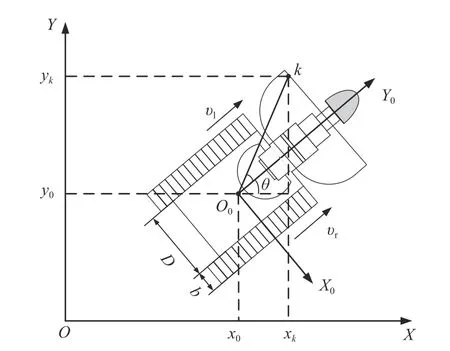
图2 掘进机器人运动学模型Fig.2 Kinematic model of cantilever roadheader robot
假设掘进机器人机身宽度为D,两轮履带宽度相等均为b,左轮履带线速度为 υl,右轮履带线速度为 υr,掘进机器人转向角为θ,掘进机器人质心在巷道平面坐标系XOY下的坐标为 (x0,y0),掘进机器人运动到目标点k过程中的线速度为 υ,角速度为ω,瞬时曲率半径为R,则掘进机器人在巷道平面坐标系XOY中的位姿可描述为P=[x0,y0,θ]T。
根据图中几何关系,可得掘进机器人左右轮履带线速度和瞬时曲率半径之间的关系为:
两式相减得:
由此可得掘进机器人的角速度为:
从而可得掘进机器人左右轮履带线速度和掘进机器人运动速度之间的关系为:
又由图2 中几何关系,可得掘进机器人运动到目标点k过程中的运动学方程为:
2.2 基于RGB-D 相机的巷道环境重建
在进行掘进机器人的机身移动路径规划时,为了观测巷道实际环境,采用RTABMAP 算法搭载RGB-D 相机对巷道环境进行实时三维重建,巷道重建过程如图3所示。
图3 巷道重建过程Fig.3 Roadway reconstruction process
RTABMAP 算法是一种结合了外观信息和深度信息的实时三维环境建模算法,能够在实时场景中构建稠密的三维地图[27]。该算法通过创建里程计节点,RGB-D相机输出的图像提供视觉里程计,并对所有节点的里程计位姿进行修正来维护机器人的全局位姿。
在掘进机器人机身前侧安装Kinect v2 相机,并为其添加云台,使得该相机能够全方位旋转。当掘进机器人施工行进时,深度相机扫描得到巷道环境的三维点云数据,将其进行处理后实时存储至数据库,通过Unity3D平台实时读取数据库中的最新数据,进行坐标匹配形成新的点云坐标,并对其进行实例化,实现虚拟环境中巷道模型的实时更新,从而完成巷道模型的实时重建,为掘进机器人与巷道侧壁之间的碰撞检测提供了条件。
2.3 虚拟环境碰撞检测模型建立
掘进机器人与巷道侧壁之间的碰撞检测是掘进机器人移机过程中的重要一环,本文采用层次包围盒算法检测掘进机器人与巷道侧壁之间的碰撞行为。层次包围盒算法计算时间短[28],能够通过建立简单的立体几何形状近似代替复杂的三维模型,可以有效降低碰撞检测原有模型的计算复杂性。
为确保掘进机器人的安全运动空间,对巷道侧壁添加了膨胀1.2 倍的盒形碰撞器(Box Collider),其中膨胀倍数为碰撞检测的安全阈值。掘进机器人模型形状复杂,若只采用一种包围盒近似代替其形状,会因为模型包裹紧密性差,冗余空间大,造成碰撞检测的误判。因此,为提高掘进机器人与巷道侧壁之间碰撞检测的准确性,同时采用多种包围盒对掘进机器人模型进行混合包围,由于掘进机器人机身形体较为规则,则机身部分采用盒型碰撞器进行包围,截割臂部分形体复杂,采用网格碰撞器(Mesh Collider)进行包围,添加效果如图4 所示,碰撞检测效果如图5 所示。

图4 包围盒添加效果Fig.4 Bounding box

图5 碰撞检测效果Fig.5 Collision detection
在路径规划过程中,当掘进机器人与巷道侧壁的包围盒发生接触或相交时,触发碰撞效果,被碰撞的物体颜色变为红色,掘进机器人动作停止,训练场景重置,退出触发碰撞效果时,被碰撞的物体恢复原来颜色,重新进行路径规划过程;当掘进机器人与巷道侧壁的包围盒未发生接触或相交时,掘进机器人处于安全运动空间内,则继续执行路径规划过程。
3 基于智能体的掘进机器人路径规划
煤矿井下掘进工作面通常是狭长巷道,而掘进机器人形体较大,运动方式复杂,因此需要考虑掘进机器人的形体大小进行路径规划。传统的路径规划方法大多将机器人当作质点处理,难以适应井下巷道空间受限条件下的掘进机器人路径规划。本文采用深度强化学习(Deep Reinforcement Learning,DRL)技术对掘进机器人进行路径规划,提出了基于柔性动作-评价(Soft Actor-Critic,SAC)算法的后见经验回放(Hindsight Experience Replay,HER) HER-SAC 算法,并定义智能体状态空间与动作空间,设计奖惩函数,使智能体能够快速找到安全的可行路径。
3.1 改进SAC 算法
SAC 算法是一种基于策略梯度(Policy Gradient)和Q-learning 的混合算法,其核心思想是在最大化累积奖励的同时还会最大化熵,通过增加策略熵的期望来增强智能体探索的能力,提升随机策略性能[29]。SAC 算法的目标函数为:
在SAC 算法中,策略被表示为一个神经网络,它通过接收当前状态作为输入,输出动作的概率分布。Q值函数也被表示为一个神经网络,它接收当前状态和动作作为输入,输出一个Q值。为了减少过估计的风险,SAC算法使用了两个Q值函数。因此,SAC 算法有5 个网络结构,即1 个Actor 网络(策略网络)、2 个VCritic 网络(状态价值估计V和TargetV网络)、2 个QCritic 网络(动作-状态价值估计Q0和Q1网络),如图6 所示。

图6 SAC 算法网络Fig.6 Network of the SAC algorithm
将任意状态st作为输入,Actor 网络输出所有动作的概率为π(a|st),并且根据概率采样获得动作at∈a,将动作at作用于Agent,得到该状态下的奖励值rt,并移至下一状态st+1,从而获得当前状态下的经验元组(st,at,rt,st+1),然后将该元组回放入经验池。
在QCritic 网络更新过程中,通过对经验池采样获取数据 (st,at,rt,st+1) 来更新参数λ,状态st下的预测价值估计以网络输出的动作at的Q(st,at)值来代替,基于最优Bellman 方程可以得到状态st下的真实价值估计:
通过均方损失函数(MSELoss 函数)对QCritic 网络训练,则其损失函数为:
VCritic 网络的更新主要是从经验池采样获取数据(st,at,rt,st+1) 来更新参数β,并采用均方损失函数对VCritic 网络进行训练。在进行Actor 网络的更新时,通过梯度下降训练得到的损失函数为:
由于掘进机器人属于履带式机器人,在狭长巷道中的运动方式复杂且路径规划过程目标单一,难以达到训练效果。同时为避免奖励稀疏,提高智能体的学习效率,将后见经验回放引入SAC 算法,提出HER-SAC 算法,通过将失败的经验转化为成功的经验来增加训练数据,从而加快训练速度。
训练智能体时做如下规定:
(1)定义多目标集合G,对于任意目标g∈G,都有fg(s)∈{0,1} 。该函数表示当fg(s)=1时,状态s到达目标g;fg(s)=0时,状态s未到达目标g。
(2)目标g可以是状态s,也可以是状态s的映射。
(3)将目标g下的奖励函数定义为一个二值奖励函数rg(s,a)=-[fg(s)=0],当状态s未到达目标g时就返回-1。
根据环境给予的目标g和初始状态s1,智能体与环境交互采集样本得到轨迹:{s1,a1,r1,s2,···,sT},并将其以状态元组 (st‖g,at,rt,st+1‖g)的形式回放入经验池,此时这条轨迹的数据是基于目标g的。在这条轨迹中随机选取n个当前遍历状态之后的状态组成目标子集G′,将这轮样本当前状态的目标依次修改为其他目标g′∈G′,得到新的奖励值r′=(s,a),则状态st对应的状态元组变为 (st‖g′,at,,st+1‖g′),然后将这条轨迹基于目标g′的所有状态元组进行回放,则经验池中存放的样本数目变为原先真实采样数目的n+1 倍,大大增加了训练样本。其中,st‖g为当前状态st与本轮样本目标g的附加拼接。
同时,策略是与目标相关的,其输入是当前状态和本轮需要完成的目标,可表示为π(st‖g)。由于本文针对的悬臂式掘进机的移机路径规划属于单目标任务,因此所有策略是基于目标g得到的,采样的数据也是不断向着目标g的方向进行的。
算法流程见表1。

表1 HER-SAC 算法流程Table 1 HER-SAC algorithm workflow
3.2 定义智能体状态空间与动作空间
状态空间代表智能体感知的环境信息,它是智能体做出决策并对其长期效益进行评价的基础,合理地进行状态空间设计可以保证算法稳定收敛,提升算法性能[30]。掘进机器人在非全断面巷道作业条件下的移机过程中需要明确其目标位置、与巷道侧壁的安全运动范围,从而采取合理的动作与巷道侧壁不发生碰撞,安全到达目标位置。因此,智能体的状态空间可定义为St={Tt,Ot,αt,Dt},其中Tt为智能体需要到达的目标位置,Ot为智能体的实时位置,αt为智能体的实时航向角,Dt为智能体与巷道侧壁发生碰撞情况。
动作空间是机器人与环境交互的方式[31]。由于掘进机器人存在转向和直行两种运动方式,因此,智能体的动作空间可定义为At={υt,ωt},其中 υt为智能体前向运动速度,ωt为智能体运动角速度。
3.3 奖惩函数设计
智能体在寻优探索的过程中,奖励函数的构成,决定了算法寻优的方向和智能体学习的动作[32]。设计奖惩函数是为了使智能体通过奖惩机制快速找到安全到达目标位置的最优路径。本文设置奖惩函数有如下内容:
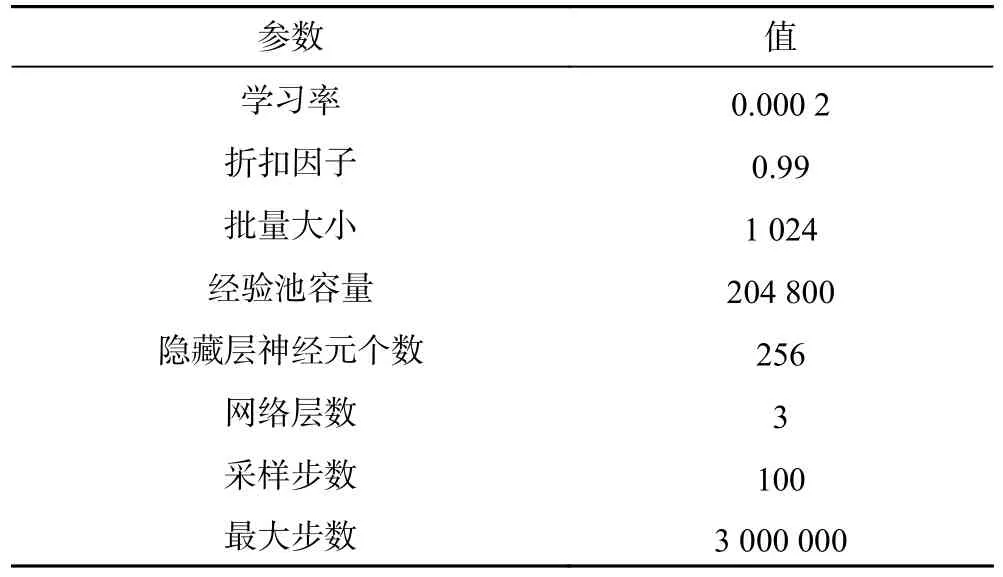
(1)通过智能体的实时位置与目标位置的距离来判断是否到达目标位置,若成功到达目标位置,获得奖励Rarrive=1.5,结束该回合;为避免奖励过于稀疏,在智能体运动过程中,记智能体上一时刻与目标位置的横向距离为xt-1,智能体当前时刻与目标位置的横向距离为xt,若xt (2)智能体通过包围盒之间的相交检测判断是否发生碰撞,为保证智能体的安全运动空间,将巷道侧壁的包围盒膨胀了1.2 倍。当触发碰撞时,获得惩罚Rcollision=-0.5,结束该回合。 (3)根据实际巷道作业规程,掘进机器人前后移动距离不能过长,因此,需要对智能体添加前后移动距离约束,若智能体的实时位置超出前后移动距离约束范围,获得惩罚Rz=-0.5,结束该回合。 (4)为缩短智能体到达目标位置的时间,提高训练效率,在智能体动作后的每一步设置外部奖励Rt=-0.005。 因此,本文的奖励函数为: 在Unity3D 平台中建立智能体,基于Python 语言设计HER-SAC 算法,通过本地Socket 实现Unity3D与Python 的交互,进行智能体的训练。HER-SAC 算法主要参数设置见表2。 表2 HER-SAC 算法主要参数设置Table 2 Main parameters of the HER-SAC algorithm 为了更清楚地观察训练结果,在相同场景条件下分别使用HER-SAC、SAC、PPO 3 种算法对智能体进行训练,结果如图7 所示。图7a 为智能体的累积奖励变化曲线,智能体获得的奖励值越大,则其在训练过程中采取正确动作的概率越大;图7b 为智能体训练时的回合长度变化曲线,每回合的长度值越大,则其在训练过程中采取正确动作的步数越多;图7c 为智能体在训练过程中的Actor 网络损失值变化曲线,Actor 网络的目标函数是为了最大化熵和奖励值,因此其损失值为负值,绝对值越大,说明最大化熵的程度越大,智能体采取的策略越随机;图7d 为智能体在训练过程中的Critic 网络损失值变化曲线,损失值越小,说明智能体所获实际奖励值越接近理论奖励值。 图7 训练结果Fig.7 Training results 由图7a 可以看出,当训练迭代次数比较小时,智能体易与巷道侧壁发生碰撞,获得的奖励较少,训练迭代次数逐渐增大时,智能体在3 种算法下所获奖励迅速增加,其中HER-SAC 算法在获得最大奖励值时所需迭代次数最少,最快达到收敛。由图7b 可以看出,训练迭代次数逐渐增大时,智能体在3 种算法下的回合长度值不断增大,其中HER-SAC 算法的回合长度值增大的速度最快,达到最大回合长度值的迭代次数最小。由图7c可以看出,训练迭代次数逐渐增大时,HER-SAC 算法策略损失值的绝对值不断增大,最快达到收敛。由图7d 可以看出,训练迭代次数逐渐增大时,智能体在3 种算法下的损失值均逐渐减小,其中HER-SAC 算法的损失值最小时的迭代次数最少,最先达到收敛。 通过对比3 种算法的平均奖励值、最高奖励值、达到最高奖励值的步数及鲁棒性指标进行算法的性能分析,对比结果见表3,其中算法的鲁棒性指标通过智能体的平均奖励值与标准差进行描述。 表3 3 种算法性能对比分析Table 3 Comparative analysis of the performance of three algorithms 由表3 可以看出,3 种算法在性能方面,SAC 算法相比于PPO 算法的平均奖励值和最高奖励值更高,达到最高奖励值的步数更少,鲁棒性方面更优,而HERSAC 算法在4 个指标的性能上均超过了另两种算法。与PPO 算法相比,HER-SAC 算法的平均奖励值提高了5.86%,最高奖励值提高了0.39%,达到最高奖励值的步数缩短了9.89%,所获奖励的标准差降低了11.75%;与SAC 算法相比,HER-SAC 算法的平均奖励值提高了5.15%,最高奖励值提高了0.28%,达到最高奖励值的步数缩短了6.69%,所获奖励的标准差降低了7.64%。 为了进一步验证本文所提方法的可靠性,基于Unity3D 平台搭建掘进机器人路径规划实验平台,采用虚实结合的方式对掘进机器人的机身路径规划功能进行验证。 实验平台分为软件平台和硬件平台,其中软件平台主要由设备状态监测模块、环境监测模块、掘进机器人位姿参数显示模块和远程控制模块组成,如图8 所示,硬件平台采用履带式机器人代替掘进机器人,以实验室楼道作为巷道环境,如图9 所示。 图8 路径规划实验软件平台Fig.8 Experimental software platform for path planning 图9 路径规划实验硬件平台Fig.9 Path planning experimental hardware 虚实结合的方式能够有效应用的前提是虚实空间中机器人的位姿时刻保持一致,因此需要对虚实空间中机器人动作的同步性进行测试。 上述实验平台中巷道环境尺寸为200 cm×200 cm,掘进机器人尺寸为70.0 cm×68.5 cm,以巷道左下角作为坐标原点,宽度方向作为x轴,长度方向作为y轴,建立巷道坐标系。通过软件平台中的远程控制模块下发控制指令,远程控制机器人动作,机器人机身上的传感器数据传输至软件平台中对虚拟空间中的机器人位姿进行动态修正,从而保证虚实空间中的机器人动作保持一致。通过实时观测虚实空间中机器人执行一次路径规划任务过程中的位姿数据,以t=1 s 的采样周期,采集31 个位置处的x方向坐标数据、y方向坐标数据和航向角数据进行对比,如图10 所示。 图10 掘进机虚实空间位姿对比Fig.10 Comparison of the virtual and real space movements of cantilever roadheader robot 由图10 可以看出,掘进机器人在运动过程中物理空间和虚拟空间的x方向坐标、y方向坐标和航向角基本保持一致。 为了更清楚地对比机器人在虚实空间中的位姿数据,将机器人在此过程中经过的路径起点、路径终点和路径关键点处的(x,y)坐标和航向角数据进行对比分析,见表4。x方向坐标的误差在1.57 cm 以内,y方向坐标的误差在1.79 cm 以内,航向角的误差在0.78°以内,满足虚实同动的性能要求。 表4 虚实空间数据对比分析Table 4 Comparative analysis of virtual and real space data 通过上述实验验证了机器人在虚实空间中的动作同步性,因此本文通过虚实结合的方式可直观地展示路径规划结果。 以上述实验平台为基础,设置掘进机器人初始位置坐标为(90,100),在此条件不变的情况下,通过调整目标位置设置两种场景并分别使用SAC 算法和HERSAC 算法对掘进机器人进行路径规划。 第一种场景(近距离)中的目标位置的坐标为(115,100),距离机器人初始位置较近,分别将虚拟空间和物理空间中机器人的路径结果记录如图11 所示;第二种场景(远距离)中将目标位置的坐标设置为(145,100),距离机器人初始位置较远,分别将虚拟空间和物理空间中机器人的路径结果记录如图12 所示。 图11 近距离路径规划结果Fig.11 Results of short path planning 图12 远距离路径规划结果Fig.12 Results of long path planning 由图11 可以看出,近距离条件下,两种算法规划的路径效果良好,HER-SAC 算法相比SAC 算法路径纵向移动距离更短,路径的平滑性更好;由图12 可以看出,远距离条件下,HER-SAC 算法相比SAC 算法效果更好,纵向移动距离更短,路径更加平滑。 为进一步分析本文所提算法的性能,分别统计了两种算法在两种场景下的路径长度、拐点数及路径终点与目标位置的距离,见表5。近距离条件下,HER-SAC算法比SAC 算法,路径长度更短,拐点数更少,终点更接近目标位置;远距离条件下,HER-SAC 算法的路径长度更短,拐点数更少,终点与目标位置的距离更小,达到最优路径,而SAC 算法的路径长度较长,拐点数较多,并非最优路径。 表5 路径结果对比Table 5 Comparison of results between long and short path planing 综上所述,本文所提算法在两种场景下规划出的路径更加平滑,路径长度更短,能够更好地适应不同的目标位置,高效地完成路径规划任务,为掘进机器人的移机轨迹跟踪控制奠定基础。 a.根据煤矿井下非结构化环境特征及掘进机器人运动特性,提出了巷道边界受限下的避障策略,基于奖惩机制建立了智能体,采用深度强化学习方法实现了掘进机器人的移机路径规划,实验结果表明该方法能够获得长度更短、更加平滑的路径。 b.将后见经验回放引入SAC 算法中,提出了HERSAC 算法,根据初始环境目标获得多目标子集,增加经验池样本数据,提高了算法的收敛速度和训练效率。用3 种算法在同一场景条件下进行训练,训练结果表明该算法相比另外两种算法性能达到最优,能够更高效地完成路径规划任务。 c.采用虚实结合的方式对所提方法进一步验证,通过对比分析不同场景下2 种算法的路径结果,验证了本文所述方法的准确度和鲁棒性,为煤矿掘进设备自动化提供了新方法。由于实际煤矿井下巷道环境复杂多变,后续还需深入研究巷道环境构建、机器人运动控制等内容,实现非全断面巷道智能化作业,提高掘进效率。 符号注释: at为t时刻的动作;为策略π在下一步采取的所有可能动作;B为从经验池中取一个batch(批量)的样本数据量;Eπ为策略π在状态st+1下的累积回报期望;为策略π在状态-动作对 (st,at)下的回报期望;为策略π在状态st下采取动作的回报期望;H(π(·|st)) 为策略π在状态st下的熵;P˙为掘进机器人的位姿矩阵;Q(st,at;λ)为QCritic网络输出的状态动作对(st,at)下的预测价值估计;Q(st,;λ)为QCritic网络输出的状态动作对(st,)下的预测价值估计;rt为状态-动作对 (st,at) 的回报值;r(st,at) 为状态-动作对 (st,at)下的回报值;st为t时刻的状态;t为时间步数;T为时间参数;、分别为掘进机器人在巷道平面坐标系XOY下沿x轴、y轴方向上的线速度;α为正则化系数;β为Actor 网络参数;γ为折扣因子;为掘进机器人运动角速度;λ为QCritic 网络参数;π为一个状态下采取一个动作的概率;lnπ(;β) 为策略π在状态st下的熵;ρπ为t=0 到T所有状态-动作对的集合。3.4 智能体训练结果分析


4 实验与结果分析
4.1 掘进机器人路径规划实验环境搭建
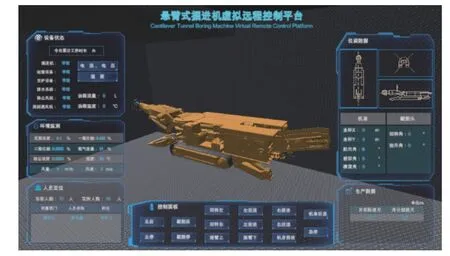

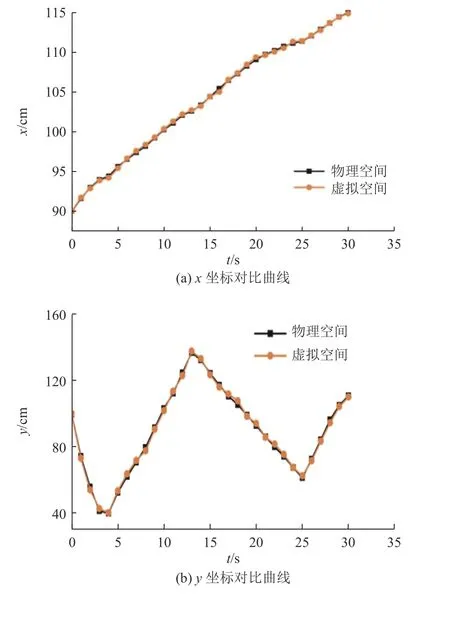
4.2 掘进机器人虚实同动实验验证

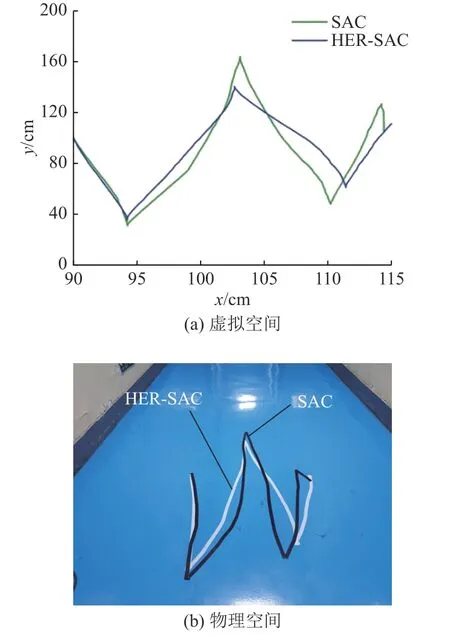
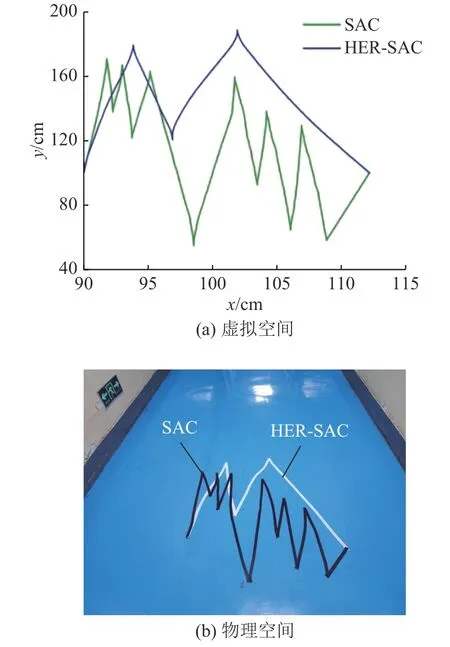
4.3 掘进机器人路径规划实验结果及分析

5 结论

