基于2.5D 有限元的高密度电法不同装置勘探效果研究

赵荣春，吕玉增，张 智，韦柳椰，潘泓序

(桂林理工大学 地球科学学院，广西 桂林 541004)

高密度电法起源于20 世纪70 年代末期的阵列电法探测思想，是在80 年代从美国和日本发展起来的一种电阻率方法[1-3]。高密度电法兼具电剖面和电测深的特点，凭借工作效率高、反映地电信息丰富、施工简便等优点，已经被广泛应用于堤坝勘查、考古、工程物探、水文地质勘探等各个方面[4-6]。

高密度电法基本理论与常规电阻率法相同，然而在诸多方面又体现出了较常规电法的优越性，高密度电阻率法具有多种排列装置，如：温纳排列、偶极-偶极排列、施伦贝谢尔排列、三极排列等排列装置，不同装置因其自身的排列方式不同，其在不同测量环境下表现出的探测效果往往有着很大的差异性。因此，在实际工作环境中针对不同探测对象选择合适的排列装置就显得尤为重要，为探究高密度电法不同排列装置的探测效果，前人在实践应用及数值模拟方面都做了诸多研究。在实践应用中，杨佳鸣[7]、李文忠[8]等对具有明显层状结构的断崖剖面，分别采用温纳、偶极-偶极、微分和施伦贝谢尔等装置进行对比测量，发现施伦贝谢尔装置对地层分层有较好的反映；郭清石[9]、孙忠辉[10]等采用数值模拟及模型实验的方法模拟了高密度电法对溶洞、溶槽的探测，对比发现不同装置对低阻溶洞都具有很好的分辨能力；王刚等[11]采用不同排列装置分别对地质剖面及输水管道进行勘察，对不同探测装置的分辨特点进行了分析。在电阻率法数值模拟方面，R.C.Fox 等[12]利用有限单元法，模拟了2D 构造下使用偶极-偶极装置测量时地形对探测效果的影响，结果表明地形会对探测带来显著影响；K.M.Befus[13]针对电阻率、极化率在复杂条件下的成像问题进行了研究，并在实际探测中进行了成功应用；欧阳永永等[14]通过建立高阻异常体和隐伏直立低阻体模型，分析认为温纳装置对于高阻异常体的探测优于其他装置，而对隐伏直立低阻体的探测温纳和三极装置的探测效果更好；王智等[15]采用GMSH 进行几何建模，对研究区域进行非结构化四面体网格剖分，实现了三维井地电阻率法的正演模拟；郑冰等[16]基于有限差分法对高密度电法进行了正演分析，研究发现当探测水平相邻低阻异常体时，偶极-偶极、三极、对称四极装置对异常体的探测效果优于其他装置；吴小平等[17]应用非结构化的网格剖分，对具有复杂地形条件下的三维电阻率进行了高精度的数值计算；C.Rücker[18]、T.Günther[19]等采用非结构化网格剖分实现了三维电阻率有限元正反演，提高了对复杂模型的处理能力。

在前人诸多的研究中，基于野外实际环境的研究往往会受限于地质环境本身的单一性，因此，无法对多种地质背景及异常形态进行对比研究，在数值模拟方面则缺乏对高密度电法测量进行较为系统的分析。高密度电法因其广泛的适用性，其二维和三维的正演问题仍然是电法研究的一个重要方向，实际工作中针对不同探测对象如何选择合适的测量装置以获得更好的探测效果是一个值得探索的问题。因此，笔者从点源电位在三维构造中所满足的微分方程出发，推导了2.5D 电位所满足的变分问题，采用Delaunay 三角化算法实现非结构化网格剖分，实现了对高密度电法的正演，在此基础上结合野外实际应用，设计了生产实践中常见的地质模型，通过设置不同的电性参数，采用不同的高密度电法排列装置进行正反演计算，并对其探测的效果进行比较和分析，以期为高密度电法勘探的实际应用提供参考和优化策略。

1 2.5D 有限元数值模拟

有一定走向的构造称为二维构造，可以用2 个坐标变量描述二维构造的地电特征，但是点电源产生的电场是三维的，因此，点源二维构造的电场其实是三维的，可采用傅里叶变换，将三维电场变换成带参数的2.5D 问题，进而使用有限单元法求解。

1.1 稳定电流场电位边值问题

稳定电流场中单点源存在的情况下电导率分布均匀的3D 边值问题可表示为[20]：

当地质体的电性分布沿某一方向不变时，三维问题可以通过傅里叶变换转化为2.5D 问题[21]。

将方程(2)应用于方程(1)，可得：

用有限单元法求解方程(3)所示的边值问题，需先将其变换成对应的变分问题[20]，之后进行数值求解。

1.2 有限单元法

为求解方程(3)所对应的变分问题，本文采用有限单元法(Finite Element Method，FEM)[22]在Matlab 中进行数值求解。有限单元法求解的基本思想是将研究区域离散成一组单元，其中的未知电位V由与节点相连的简单线性插值函数近似表示，因此，必须创建相应的网格进行计算。本文采用Delaunay 三角化算法实现非结构化网格剖分，并对研究区域进行局部加密[23-24]。经过相应的积分变换，方程(3)可表示为[22]：

将方程(4)所示的单个的有限元矩阵结合在一起创建一个线性方程组可表示为：

解线性方程组(5)可得到各节点的电位。当方程(5)求解完毕后需将波数域的计算结果通过反傅里叶变换式(6)将其转换到实数域中，以获得测点的真实电位V。

最优化算法中，一般采用数值计算下式代替式(6)的计算，计算离散波数和加权系数的方法可以在文献[25]中找到，这里不再重复。在本文的计算中，将使用高斯求积和拉盖尔积分的组合方法[26]进行求解。

1.3 数值模拟精度分析

为验证正演程序的正确性，分别采用数值模拟与球形异常体解析式进行计算[27]。

低阻球体模型参数设置为：球心距地表h=5 m，球体半径ra=2 m，低阻球体的电阻率ρ2为50 Ω·m，围岩的电阻率ρ1为1 000 Ω·m，采用施伦贝谢尔装置观测，取极距为15 m 作剖面，如图1 所示。分析可见，数值计算结果与解析解基本吻合，解析解与数值解平均相对误差不超过1.5%，正演计算具有较高的精度。

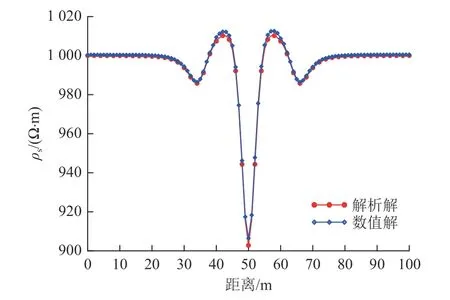
图1 数值解与解析解对比Fig.1 Comparison between numerical and analytical solutions

2 模型算例与结果分析

2.1 排列装置及测线布设介绍

高密度电法勘探主要有温纳、偶极-偶极、施伦贝谢尔、二极、三极等排列装置，以此为基础，又演变出了十几种装置类型，本文将针对实践中应用较为广泛的温纳α、温纳β、施伦贝谢尔、偶极-偶极装置进行研究，在模型计算中统一设定测线长为400 m，电极距为10 m，共布设40 个电极。在反演计算方面，目前市面上有众多反演软件及相关的算法，然而瑞典RES2DINV 反演软件应用最为普遍，因此，本文将以此对数值结果进行最小二乘法反演计算，在反演计算中，设置阻尼系数最大值为0.1，最小值为0.03，最大迭代次数为5 次，收敛极限为5%，不使用圆滑约束。导出反演数据用Surfer绘制反演剖面图，正演剖面中以1/4 最大电极距近似表示深度。

本文中各排列装置电极排列如图2 所示。在温纳α、温纳β排列中，A、B、M、N电极间距离始终固定相等，隔离系数t在测量中逐渐增大；在施伦贝谢尔测量中，AM=BN，系数t逐渐变大，系数m随着t的变大进行调整，m的变化范围为1～5；在偶极-偶极装置测量中，AB=MN，系数t逐渐变大，系数m随着t的变大而调整，变化范围为1～3。

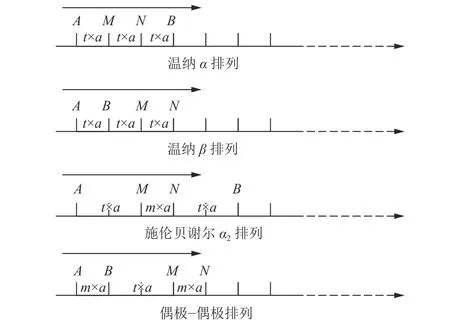
图2 不同排列装置电极分布Fig.2 Electrode distributions in different array configurations

2.2 水平层状介质模型

建立如图3 所示水平层状介质模型，用以探究高密度电法对覆盖层的测量效果及各装置的垂直分辨率，设计覆盖层厚度为20 m，电阻率为300 Ω·m，下方基岩电阻率为2 000 Ω·m。

图3 水平层状介质模型网格剖分Fig.3 Gridding of a horizontal layered medium model

图4 为水平层状介质模型视电阻率正反演剖面。综合分析可见，无论是正演剖面还是反演剖面，4 种装置对地层都有较好的分层效果，地层界限与理论模型20 m 的深度基本对应，覆盖层电阻率大小接近设计值300 Ω·m。对比正反演的成果，可见视电阻率正演剖面岩层界限清晰且没有其他干扰异常的出现，反观反演剖面则可见一些干扰信息，如温纳α法中出现了明显的高阻圈闭异常(图4b)，温纳β中出现了高阻基岩的断裂(图4d)，这些干扰信息都有可能导致在处理实际问题时解释出现误判，因此，在地形平坦且地层分层结构明显时，不经反演的实测数据对于解释具有重要的参考价值。

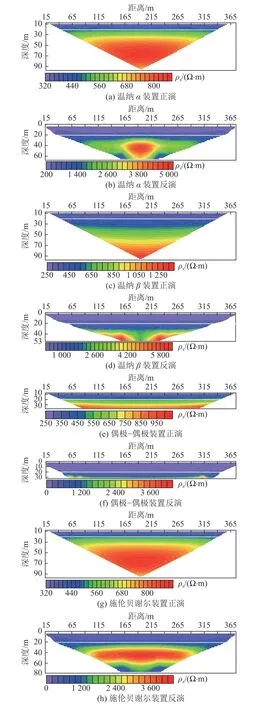
图4 水平层状介质模型视电阻率正演与反演剖面Fig.4 Forward and inversion profiles of apparent resistivity derived from the horizontal layered medium model

2.3 单个低阻、高阻异常体模型

高密度电法常被用来寻找地下低阻充水溶洞或者高阻地下空腔(如：考古、采空区)，建立如图5 所示正方形异常体模型，用以模拟低阻、高阻地质体的情况。设计异常体位于测线中央正下方，异常体中心位于水平方向200 m 处，异常体顶部埋深20 m，边长为20 m，围岩电阻率为800 Ω·m，异常体为低阻时电阻率为50 Ω·m，为高阻时电阻率为5 000 Ω·m 。

图5 正方形异常体模型网格剖分Fig.5 Gridding of a square anomaly model

图6 为低阻模型视电阻率正反演剖面。由反演剖面可见，4 种装置在异常体中心位置30 m 处都有非常明显的低阻异常现象，都可以很好地对应异常体的空间位置，相比而言，温纳β、偶极-偶极、施伦贝谢尔装置其反演效果具有更好的收敛性，低阻异常与实际模型大小及位置都有很好的对应，而温纳α正演剖面(图6a)则在中心异常的两侧出现了低阻假异常；从正演的成果上分析，温纳β、偶极-偶极(图6c、图6e)的低阻异常中心基本与实际模型位置对应，施伦贝谢尔的异常(图6g)只在水平方向上与异常位置对应很好，而温纳α的视电阻率正演剖面(图6a)则出现了类似于双低阻异常的现象，与实际模型存在很大的差距，因此，在生产实践中对于类似异常形态的解释要加以区分。

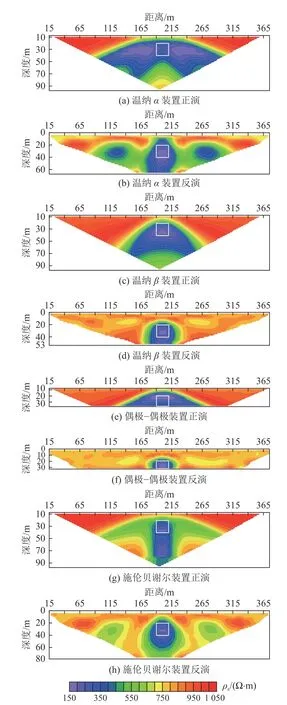
图6 低阻模型视电阻率正演与反演剖面Fig.6 Forward and inversion profiles of apparent resistivity derived from the low-resistivity anomaly model

图7 为高阻模型视电阻率正反演剖面图。由反演剖面可见4 种装置都具有很好的探测效果，高阻异常中心基本与实际模型对应，能很好地反映出高阻异常所处的空间位置；而从正演的情况分析，4 种装置的视电阻率正演剖面异常形态都很有各自的特点，相对而言温纳α的视电阻率异常形态与模型更匹配，探测效果更好。

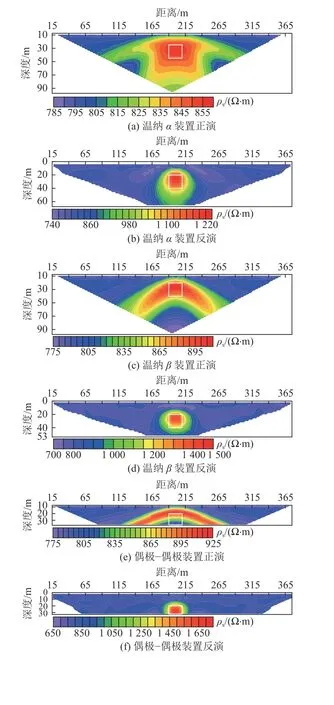
图7 高阻模型视电阻率正演与反演剖面Fig.7 Forward and inversion profiles of apparent resistivity derived from the high-resistivity anomaly model

2.4 水平双低阻异常体模型

为探究高密度电法不同排列装置在水平方向上的分辨率，设置双低阻模型(图8)，模拟当研究区域存在2 个位置相隔较近的低阻异常体时的地质结构，设置低阻体为正方形，边长都为20 m，顶部埋深为20 m，异常体中心在水平方向上的位置分别为170、230 m，两异常体之间距离为40 m，异常体电阻率为50 Ω·m，围岩电阻率为800 Ω·m。

图8 水平双低阻异常体模型网格剖分Fig.8 Gridding of a horizontal double low-resistivity anomaly model

图9 为水平双低阻模型视电阻率正反演剖面。由正演剖面可见，温纳α、温纳β、偶极-偶极(图9a、图9c、图9e)这3 种装置都显示为以水平方向200 m 为中心的单个低阻异常形态，无法反映出预设的双低阻异常体的存在；而施伦贝谢尔的正演剖面(图9g)则出现了明显的低阻双异常现象，且低阻异常中心位置与预设模型对应很好。分析反演剖面可见，4 种装置都出现了明显的低阻双异常形态，尤其是偶极-偶极与施伦贝谢尔装置(图9f、图9h)，低阻异常在空间位置上与预设模型具有很好的对应关系，而温纳α与温纳β(图9b、图9d)的低阻异常范围收敛效果则相对差一些，但仍能反映出低阻异常体所处的空间位置。

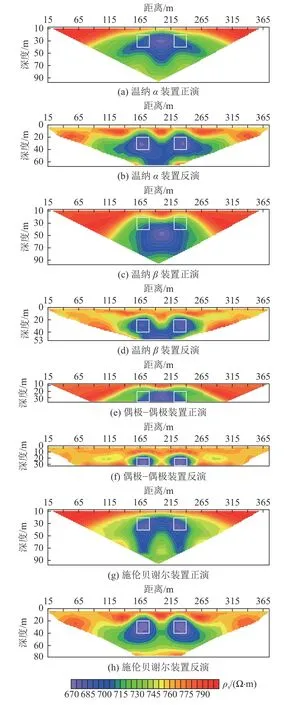
图9 水平双低阻模型视电阻率正演与反演剖面Fig.9 Forward and inversion profiles of apparent resistivity derived from the horizontal double low-resistivity anomaly model

2.5 断层破碎带模型

断层破碎带为岩石在构造运动下发生断裂形成，在漫长的地质作用下，其上部通常被第四系沉积物所覆盖，而破碎带中常被岩石碎屑、土壤等所填充，常为地下水渗流通道，因此，在地质找水中破碎带是重要的目标体。由于破碎带处地质结构相对不稳定，也是道路施工及隧道掘进过程中所要重点查明的对象，针对破碎带探测的研究具有非常重要的现实意义。根据破碎带的特征，设计如图10 所示断层破碎带模型，设定覆盖层厚度为20 m，电阻率为500 Ω·m，下伏基岩电阻率为2 000 Ω·m，破碎带电阻率为50 Ω·m，倾斜角为60°，宽度为10 m，其顶部位置位于测线水平方向230～240 m 处。

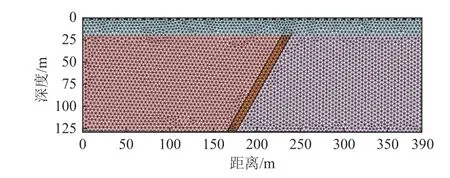
图10 断层破碎带模型网格剖分Fig.10 Gridding of a fault fracture zone model

图11 为断层破碎带模型视电阻率正反演剖面。分析各装置正演剖面可见，温纳α与施伦贝谢尔装置所示剖面(图11a、图11g)在破碎带处整体呈高阻，不能反映出低阻异常的存在，而温纳β与偶极-偶极装置的剖面图(图11c、图11e)则在破碎带处呈现出明显的低阻异常圈闭；在反演剖面中，温纳β与偶极-偶极装置的剖面(图11d、图11f)在破碎带位置也存在明显的低阻异常圈闭，而温纳α的反演剖面(图11b)在破碎带处呈现出断开的低阻异常，且低阻的形态与破碎带的倾斜方向大致相当，施伦贝谢尔装置的低阻异常形态与温纳α的大致相当，相比之下施伦贝谢尔装置的低阻异常相对较弱。

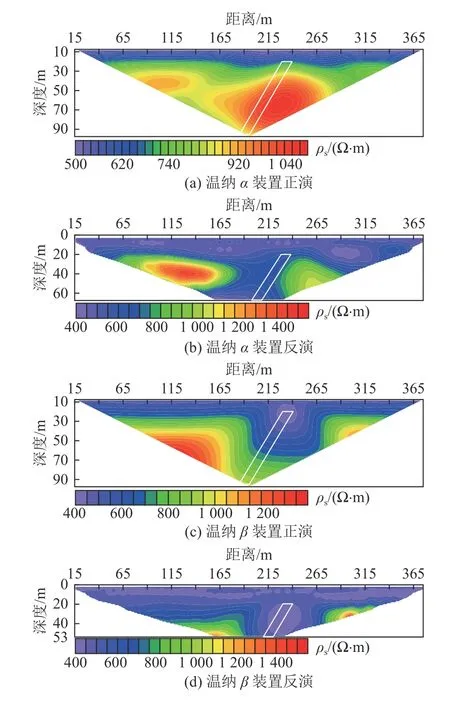
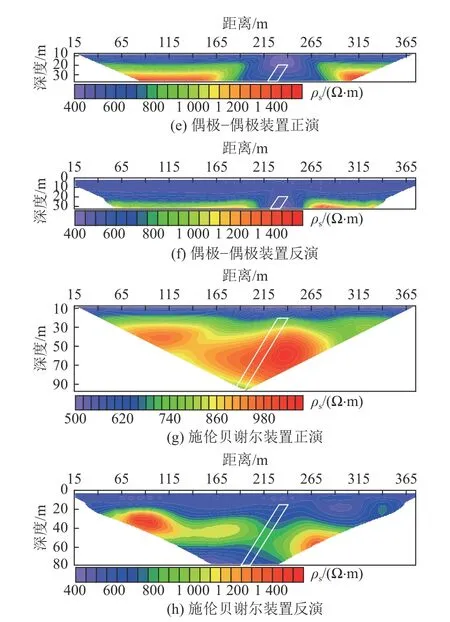
图11 破碎带模型视电阻率正演与反演剖面Fig.11 Forward and inversion profiles of apparent resistivity derived from the fault fracture zone model

3 结果与讨论

高密度电法在实际应用中，地下介质的复杂性和多样性使得电法数据解释变得复杂，不同地质体的电性参数差异、地下水体的存在、岩性变化以及构造扰动等因素都会影响数据的解释。因此，构建不同的地质模型，采用多种采集方式进行分析研究，对于提高高密度电法的分析解释精度具有重要的作用。笔者采用非结构化网格剖分进行有限元数值模拟，解析解与数值解平均相对误差不超过1.5%，正演计算具有很高的精度，可以有效地模拟各种类型的地质模型。在此基础上结合实际应用，设计了生产实践中常见的5 种地质体模型，并分别采用了温纳α、温纳β、施伦贝谢尔、偶极-偶极4 种排列装置进行了电阻率的正反演对比研究。

通过对水平层状介质模型的分析，验证了高密度电法在探测覆盖层时的有效性，各装置均展现出了良好的分层效果，然而反演剖面中显示了一些干扰信息，如高阻圈闭异常和高阻基岩的断裂，这些干扰信息可能导致解释误判，需要引起注意；综合单个低阻和高阻模型的情况对比分析可见，温纳β、偶极-偶极、施伦贝谢尔装置无论是正演剖面还是反演剖面，其电阻率的异常形态基本都是一致的，只有电阻率数值上的差别，而温纳α对于单个低阻体的探测其效果较差，而在探测单个高阻体时又具有很好的探测效果；在对水平双低阻异常体模型的分析中，发现不同排列装置在水平方向上的分辨率不同，施伦贝谢尔装置在探测双低阻异常体时表现出较好的效果；高密度电法不同装置在对断层破碎带的探测中，不同排列装置其正反演剖面上展现出了不同的探测效果，尤其是温纳α与施伦贝谢尔的正反演结果其形态上差异较大，因此，对于高密度电法数据的解释必须结合正反演剖面进行综合解释才能得出更准确的结论。

4 结论

a.高密度电法具有多种电极排列装置，如温纳α、温纳β、施伦贝谢尔、偶极-偶极等。在针对不同的地质目标和测区环境时，常表现出明显不同的探测效果和分辨能力。因此，在实际勘探工作中，应基于预先调查和人工经验，针对不同的探测对象和目标层位，选择多种合适的排列装置进行测量。对采集的多个排列装置数据进行综合分析对比，可获得更为全面准确的解释结果。

b.同一排列装置在正演和反演计算所得的视电阻率异常形态上存在一定差异。正演剖面能更直观展现目标体的空间位置，但也可能出现一些与实际情况不符的异常，如温纳α对单个低阻立方体及低阻破碎带的正演效果较差。而反演剖面虽能较好揭示目标体异常特征，但也可能产生一些干扰异常信息，如温纳α出现高阻圈闭异常等。因此，在数据解释时，需要结合正演和反演2 种结果综合分析，避免片面性导致的误判。特定目标体的解释应优先参考能更好反映其异常特征的计算结果。

c.在探测未知区域单个异常体时，综合考虑探测精度和工作效率，温纳β、施伦贝谢尔排列具有更佳效果。当预计区域存在多个异常体时，应优先采用具有较好水平分辨能力的施伦贝谢尔和偶极-偶极排列。对于低阻破碎带等类型异常，温纳α和偶极-偶极排列将获得更好的探测结果。而在存在明显分层界限的地层中，上述4 种排列均可体现出较好的分层效果。

符号注释：

a为电极间距；dA为点电源A到球心D的距离；F为电源项和边界条件；gi为加权系数；H为一个L×L阶的稀疏矩阵；H1i和H2i为仅依赖于节点坐标和单元形状的有限元矩阵；i为离散波数的个数；I为电源；k为波数；ki为离散波数；K0(kr)和K1(kr)分别为零阶和一阶贝塞尔函数；L为节点总数；ls和l∞分别为变换后的地面及无穷远边界；n为勒让德函数阶数；n′为边界的外法向向量；N为离散波数的上限；Ne为网格单元的个数；r为测点至点源的距离；rM为球心D到测量极M的距离；RAM为供电电极A到测量电极M的距离；t为隔离系数；为A点电源对M极施加的电位；V为电位；V˜ 为经傅里叶变换后波数域电位；V˜′为包含每个节点的电位；δ(x0)δ(y0)δ(z0)为以点源为中心的Dirac 函数；(x0,y0,z0) 为点源的位置；σ(x,y,z)为电导率分布函数；Ωs为傅氏变换的剖面；Ωt为研究区域；Γs为地面边界；Γ∞为无穷远边界；ρ1为围岩的电阻率；ρ2为低阻球体的电阻率；ps为视电阻率；μ为ρ2/ρ1的值；Pn(cos∠ADM)为n阶勒让德函数；∇为矢量微分算子。