一种估计外力矩的机器人直接示教方法

王振斌，李 笑，武交峰

（1.广州启帆工业机器人有限公司，广东 广州 510700；2.广东工业大学机电工程学院，广东 广州 510006）

1 引言

随着科技的不断进步，机器人越来越具备灵活操作性、友好性和开放性等特点。目前，工业和协作机器人通常都利用示教器规划运动轨迹，该方法操作效率低、繁琐，且要求操作者有一定的机器人操作基础。为了快速、便捷和友好的生成机器人复杂运动轨迹，可通过直接示教的方式，即操作者拖动机器人按特定轨迹运动的示教方式。为实现良好的拖动效果，一般使用力传感器来实现，然而力矩传感器的零点容易漂移且价格较为昂贵。因此，研究机器人的无力矩传感器直接示教方法具有重要的技术经济意义。

近年来，国内外较多学者对机器人直接示教技术开展了相关研究。文献[1]等在机器人末端安装多维力传感器以实时反馈操作者对末端的牵引信息。在机器人关节电机处于位置模式下，控制器将末端的受力转化为机器人关节运动增量，从而使机器人能够跟随操作者的牵引运动，但是该方案末端感知区域有限且成本高昂。文献[2-3]等设置机器人关节电机为力矩模式，通过实时给机器人关节补偿拖动其所需克服的重力和摩擦力力矩来实现直接示教，该方案是一种力开环示教方式，其灵敏度依赖于动力学模型的准确程度，而精确的动力学模型很难获得。文献[4]等设置机器人关节电机为位置模型，通过导纳控制将关节力矩观测器观测的外力转化为关节的位置增量，从而实现机器人的拖动，但该方案的灵活性和柔顺性欠佳。

针对以上问题，提出一种估计外力矩的机器人直接示教方法。在电机状态处于力矩模型下，通过机器人的状态和动力学模型以及基于广义动量的力矩观测器计算当前时刻机器人所需补偿的重力矩、摩擦力矩和操作者的牵引外力矩。该直接示教方法具有系统成本低、操作方便灵活和柔顺性好等优点。

2 直接示教方案

估计外力矩的机器人直接示教方法中重力矩和摩擦力矩作为前馈补偿，关节的估计外力矩由基于广义动量力矩观测器观测的外力矩，经过导纳与PD控制转化所得，作为反馈补偿。机器人连杆重力和关节摩擦力模型通过辨识获得。

2.1 控制结构

估计外力的机器人直接示教原理，如图1所示。

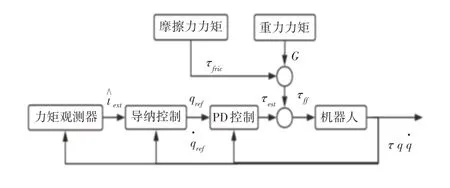
图1 估计外力矩的直接示教原理图Fig.1 Schematic Diagram of Direct Teaching for Estimating External Torque

拖动机器人运动时，实时补偿机器人估计外力矩向量τest、关节摩擦力力矩向量τfric和重力矩向量G，其中摩擦力力矩和重力矩向量组成了前馈补偿向量τff，估计的外力矩向量τest是通过PD控制算法得到的反馈补偿，具体计算公式为：

式中：Kp—系统刚度系数向量；KD—系统的阻尼系数向量；qref—关节期望的位置向量ref—关节期望的速度向量；q—关节实际的位置向量—关节实际的速度向量。

关节期望的角加速度通过导纳控制计算得到，如式（3）所示。关节期望的角速度与位置由角加速度积分所得。

式中：M—惯性矩阵ext—观测的关节外力力矩向量；D—阻尼对角矩阵，对角线元素均为常数。

2.2 辨识重力和摩擦力模型

准确的连杆重力与关节摩擦力模型一般通过辨识相关的动力学参数获得。

2.2.1 机器人动力学模型

n自由度刚体机器人动力学模型为：

式中：C(q，)—离心力和哥氏力项矩阵；τ—关节力矩向量；τext—外部环境作用于关节的外力矩向量；

关节i的摩擦力模型为：

式中：Fci—关节i的库仑摩擦力参数；Fvi—关节i的粘滞摩擦力参数。

2.2.2 参数辨识

动力学参数由惯性参数和摩擦力系数组成［5］，如式（6）所示。

式中：βi—动力学参数向量；XXi、XYi、XZi、YYi、YZi和ZZi—连杆i的惯性张量项；MXi，MYi，MZi—连杆i的一阶质量矩；Mi—连杆i的质量；Iai—关节i的电机惯性矩。

机器人动力学模型相对于待辨识的动力学参数是线性的。将式（4）线性化表达为：

式中：∅(q，，)—回归矩阵；β—n个连杆的动力学参数向量，其中部分元素对动力学模型是冗余的，需要与其他元素线性组合为一个整体进行辨识。

机器人沿设计的激励轨迹运动。采集t1，…，tk时刻机器人关节的位置、速度、加速度以及力矩值，根据式（7）得到式（8）：

通过最小二乘法求解式（8）可得动力学参数向量β的值，形式如下：

2.2.3 模型验证

动力学参数辨识的精度由测量值与计算值的残差均方根εRMS来评定，εRMS值越小辨识精度越高。

εRMS表达式，如式（10）所示。

2.3 基于广义动量的力矩观测器

基于广义动量的力矩观测器，根据机器人的状态与动力学模型，观测机器人关节的牵引外力矩［6］。机器人的动力学模型满足：

机器人的广义动量表达式为：

将式（4）、式（11）代入式（12）的求导函数，化简得：

式中：r—残差；K—比例系数。

理想条件下，估计量(q，)(q)和与实际值一致，结合式（13）、式（14）对式（15）进行求导得：

将式（16）进行拉普拉斯变换，可得下式：

从式（17）可以看出，R是对Text的跟踪，稳态时，R(0)=Text(0)，因此，r可以看作是外力矩的观测值，即：

3 验证实验

使用六轴协作机器人进行直接示教实验，机器人伺服驱动器与控制器之间采用EtherCat通信协议。实验平台，如图2所示。主要的硬件型号，如表1所示。

表1 实验平台主要器件表Tab.1 Main Components of the Experimental Platform

图2 实验平台Fig.2 Experimental Platform

机器人的动力学参数存在相互耦合现象，只能得到一组最小动力学参数集。辨识机器人前三轴动力学最小参数集结果，如表2所示。其中较长的动力学参数用θ表示，具体的形式可参考文献[7-8]，辨识用的激励轨迹可参考文献[9-10]。

表2 辨识参数结果Tab.2 Results of Identification Parameters

机器人跟踪测试轨迹时采集的力矩与通过动力学模型计算的力矩对比，如图3所示。可以看出采集的力矩与通过动力学模型计算的力矩完全一致。根据式（10）计算的残差均方根，如表3所示。

表3 关节力矩残差均方根Tab.3 Residual Root Mean Square of Joint Torque

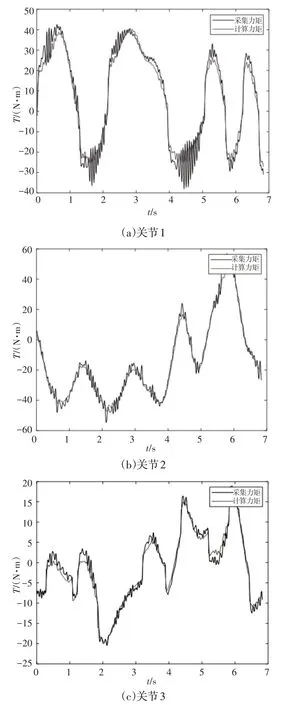
图3 机器人各轴辨识效果图Fig3 Identification Effect Diagram of Each Axis of Robot

可以看出各关节力矩残差均方根较小。综合图2和表3可以看出，辨识得到的动力学参数有较高的精度，满足工程使用要求。利用辨识得到的动力学参数和机器人当前的运动信息，可计算出各项的估计值，例如(q，)、(q)和等。

为验证所提出方法的有效性，对估计外力矩的直接示教方法与未补偿外力矩的直接示教方法进行了大量的对比实验研究。两种直接示教方法中机器人关节电机均设置为力矩模式。估计外力矩的直接示教方法给关节补偿估计外力矩、重力矩和摩擦力力矩。未补偿外力矩的直接示教方法给关节补偿重力矩和摩擦力力矩。实验时，机器人处于静止状态，操作者以相同的力从机器人零位分别拖动两种示教方法下的关节旋转一定角度后停止。每次仅拖动一个关节转动，依次对前三个关节进行了实验研究。机器人关节1、2和3的直接示教实验，如图4～图6所示。关节1在估计外力矩的直接示教实验中得到的估计外力矩，如图4（a）所示。由基于广义动量力矩观测器观测的外力矩经过导纳和PD控制转化所得。关节1的直接示教实验速度对比，如图4（b）所示。

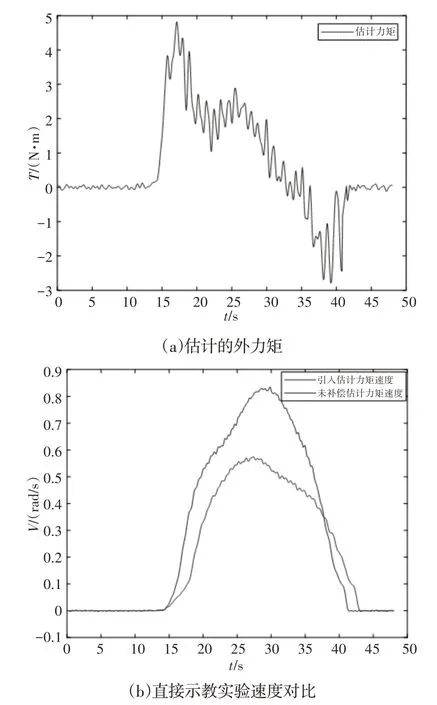
图4 关节1的直接示教实验Fig.4 Direct Teaching Experiment of Joint 1

图中引入估计力矩速度是从估计外力矩的直接示教实验中采集的速度，未补偿估计力矩速度是从无外力矩补偿的直接示教实验中采集的速度。从图4（a）可以看出，在估计外力矩的直接示教实验中，拖动机器人关节起动阶段，估计到操作者施加在机器人关节的起动外力矩。拖动机器人关节停止阶段，估计到操作者阻止机器人关节运动的外力矩。

从图4（b）可以看出，在估计外力矩的直接示教实验中，速度在起动和停止阶段的斜率明显大于无外力矩补偿直接示教实验中的，说明估计外力矩的直接示教功能具有起动和停止速度快、用时少等优点，图5、图6与图4同理。实验表明，基义广义动量力矩观测器估计外力矩的直接示教方法比无外力补偿的直接示教方法更加高效、灵敏和柔顺。

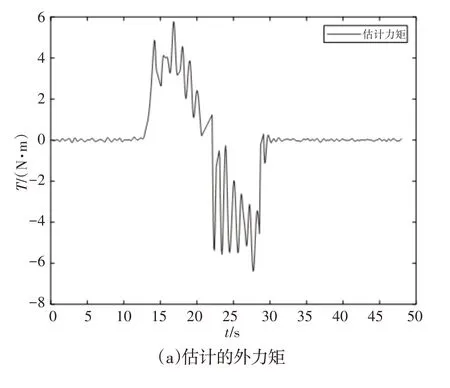
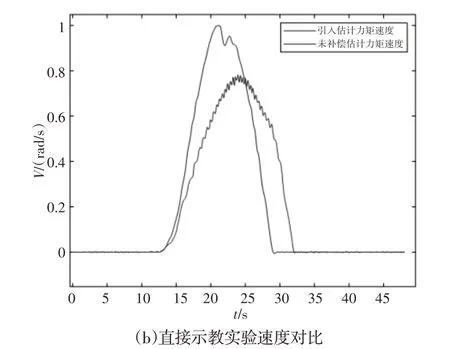
图5 关节2的直接示教实验Fig.5 Direct Teaching Experiment of Joint 2

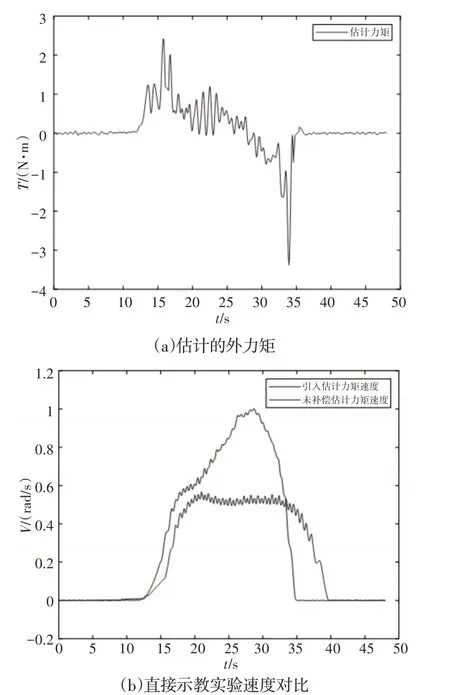
图6 关节3的直接示教实验Fig.6 Direct Teaching Experiment of Joint 3

4 结论

为解决现有直接示教灵活性、柔顺性低和成本高等问题，提出了一种基于广义动量力矩观测器估计外力矩的力矩闭环直接示教方法。实验表明，估计外力矩的无力矩传感器直接示教方法有效，可为无力传感器机器人直接示教系统设计提供指导。