新型零泊松比蜂窝结构的等效弹性参数分析

孙士勇，高 飞，杨 睿，张 雯

（大连理工大学机械工程学院精密与特种加工教育部重点实验室，辽宁 大连 116024）

1 引言

蜂窝结构具有质轻、承载力强以及吸能、降噪、隔热等特点，常被制成夹芯结构广泛应用于航空航天、交通运输、能源动力等领域[1-3]。按照泊松比的不同，蜂窝结构可以分为正泊松比蜂窝[4]、零泊松比蜂窝[5]和负泊松比蜂窝[6]。零泊松比蜂窝结构由于其在变形过程中不会出现类似于正泊松比蜂窝结构或者负泊松比蜂窝结构的马鞍形和拉涨等现象，可以作为支撑结构应用到变体飞机柔性蒙皮中[7]。文献[8]提出了一种由常规六边形蜂窝结构和内凹六角形蜂窝结构组合而成的蜂窝结构，该结构呈现出零泊松比的特性，可以作为柔性蒙皮应用到变体机翼中来实现机翼展长方向较大的一维面内变形。文献[9]提出了一种四角星形零泊松比蜂窝结构，并将该蜂窝结构作为机翼的支撑结构应用到变弯度机翼中。文献[10]提出了一种以六边形蜂窝结构和薄板组成的零泊松比蜂窝结构，可以通过对薄板进行设计进而实现整个结构弯曲刚度的变化。

蜂窝结构是一种典型的周期性结构，在进行结构设计时，采用传统的精细化有限元计算存在建模复杂、计算量大等问题，难以用于结构优化与性能评价。将蜂窝结构假设成均匀连续的材料，基于均匀化方法获得蜂窝结构的等效弹性参数用于结构的宏观性能分析是目前蜂窝结构的研究热点。文献［11］基于正六边形蜂窝结构的周期性，通过选取代表性单胞结构，建立了宏观弹性本构方程，得到了该结构的宏观等效弹性参数解析解。文献［12］利用梁模型，考虑了蜂窝壁伸缩变形和剪切变形，计算出常规六角蜂窝结构的二维等效弹性参数。文献［13］针对正六边形蜂窝结构提出了Y型等效模型，利用能量法推导了结构的二维等效性能。面对较为复杂的蜂窝构型时，目前多采用代表体元法进行等效弹性参数的分析。文献［14］通过拓扑优化的方式提出蜂窝结构近似设计方法，结合有限元方法对所设计的结构进行了性能分析。文献［15］提出了一种基于渐进均匀化的新求解方法，该方法通过利用有限元商业软件结合代表体元法，不需要复杂的数学公式推导，就可以对三维周期性材料的等效弹性参数进行预测。但是在分析不同的弹性参数时，需分别建立代表模型并施加相应的周期性边界条件进行求解。

这里提出了一种新型零泊松比蜂窝结构，采用一种新的多尺度分析方法-结构基因力学（MSG），通过将单胞结构从周期性结构中剥离出来，对单胞结构进行均匀化分析，进而得到了整体结构的等效弹性性能，并进行了精细化模型有限元数值仿真和实验，对其面内特性进行了验证；分析了等效弹性模量与蜂窝结构几何尺寸参数变化的关系，最后通过与四角星形蜂窝结构的对比，这里提出的新型蜂窝结构在面内变形能力以及抵抗面外变形的能力优于四角星形蜂窝结构，具有在变体飞机中的良好应用前景。

2 蜂窝结构设计

四角星形蜂窝［9］是一种典型的零泊松比蜂窝结构，但受限于不同蜂窝单胞之间星角处点与点的连接形式，四角星形蜂窝构成的蜂窝板结构不易实现面内弯曲变形。这里在四角星形蜂窝结构的基础上，通过在星角处引入的水平和竖直蜂窝壁，改变了原四角星蜂窝单胞之间的连接方式，构成了一种新型蜂窝结构。由于水平蜂窝壁的引入，通过对水平蜂窝壁几何尺寸的设计使结构获得不同的面内弯曲刚度，从而获得满足设计要求的结构。蜂窝单胞尺寸可以由蜂窝斜壁长L1、L2，蜂窝横壁长H，蜂窝壁角度θ，蜂窝壁厚度t和蜂窝单胞厚度b来表示，如图1所示。

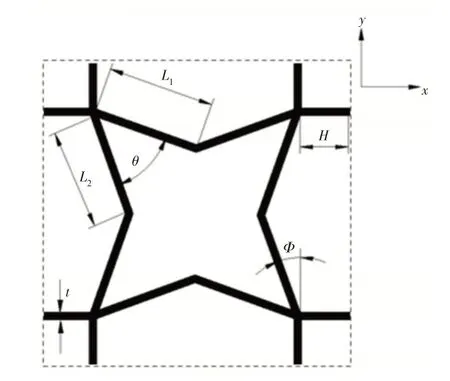
图1 蜂窝单胞几何参数Fig.1 The Geometric Parameters of a Honeycomb Unit Cell

为了便于分析，将蜂窝单胞尺寸参数进行无量纲化处理，定义无量纲参数α，β，η，其中蜂窝壁长度之比α=L12，为蜂窝壁横斜比β=1，蜂窝壁厚度比γ=。相对密度是蜂窝结构的一个重要参数，由蜂窝壁面积与蜂窝结构等效承载面积之比得到蜂窝结构的相对密度表达式：

3 基于结构基因的蜂窝单胞模型

结构基因力学（MSG）是以渐进变分法为核心，用于多尺度分析的半解析法，通过均匀化和逆均匀化来实现细观模型与宏观模型之间的信息传递，其中结构基因（SG）是记录结构信息的最小模块并作用于MSG的分析域中［16］。SG是建立在代表性结构单元（RVE）的概念之上，以强调它包含结构所需的所有组成信息，其方式与基因组包含生物体生长发育的所有内在信息相同。

MSG从原始模型开始，首先将SG识别为结构的最小单胞，然后使用最小信息损失原理（PMIL）将原始问题分解为SG上的本构建模和宏观结构分析，PMIL是通过线弹性材料的应变能密度来实现的。

在MSG中，首先，定义了宏观坐标xi和细观坐标yi，两者的关系为yi=xδ，其中，δ是一个用来描述SG模型的微小参数。宏观模型的应变场可以表示为：

式中：χ(i，j)—在细观力学中表示为波动函数，代表着宏细观两种尺度下的差异。

PMIL 使得原始非均质模型和均质模型之间的应变能差异最小化，表示为：

w用形函数来表示：

式中：S—SG单元的形函数；V—波动函数的节点分量。最终SG中的应变能函数U可表示为：

式中：C*—宏观结构模型的等效刚度矩阵；—在SG 域内的平均值。蜂窝板在宏观上是一种3维结构，表现出蜂窝单胞沿着x-y平面周期性排列的特征，建立3D SG蜂窝单胞模型，如图2所示。通过对单胞模型进行均匀化分析，获得整个蜂窝板结构的整体力学性能。

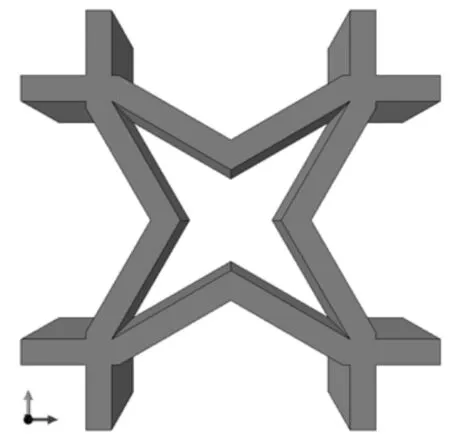
图2 3D SG蜂窝单胞模型Fig.2 3D SG for a Honeycomb Unit Cell

4 结果及分析

4.1 新型零泊松比蜂窝结构等效弹性模量分析与验证

利用有限元分析软件ABAQUS∕Standard对蜂窝结构的面内弹性参数进行分析。蜂窝结构有限元模型采用的材料为ABSM30，其材料属性由3D 打印技术制备的试件根据GB T1040.1-2066 测试标准获取，杨氏模量E=1862MPa，泊松比ν=0.3。蜂窝单胞的尺寸参数分别是L=10mm，H=5mm，Φ=30°和t=2mm，建立（7×7）的2D蜂窝结构有限元模型计算结构的面内杨氏模量、面内剪切模量和泊松比，网格单元属性为S4R，经收敛性分析后，网格尺寸设置为0.5t。建立4个参考点通过运动耦合的方式分别控制蜂窝结构的上、下、左和右边界上的节点，在上下参考点施加位移边界来获取结构的单轴拉伸变形，在左右参考点施加反对称边界条件来获取结构的面内剪切变形，详细边界条件施加，如表1所示。

表1 蜂窝结构有限元模拟边界条件Tab.1 Finite Element Simulation of Boundary Conditions of Honeycomb Structure

对7×7蜂窝结构精细化有限元模型提取中间区域蜂窝单胞结构的应力和应变信息，根据泊松比定义公式νs=-ε2-ε1计算出蜂窝结构的泊松比，面内剪切模量由G12=σshear∕εshear计算获得。为了验证精细化仿真模型（FEM）和MSG等效分析方法计算出蜂窝结构等效弹性参数有效性，引入ABAQUS 官方的代表体元法计算插件Micromechanics Plugin（MMP）［17］进行对比。

FEM模型、MMP模型和MSG模型预测的蜂窝结构的面内杨氏模量E1、面内剪切模量G12以及泊松比νs，如表2所示。其中误差1为FEM模型和MMP模型的相对误差，误差2是MSG模型与MMP模型的相对误差。从表1中可以看出，MSG模型和MMP模型对于泊松比νs的预测值与FEM模型的数值误差为-6.3%，由于泊松比近似为0，因而该误差在接受范围内。对于面内杨氏模量E1和面内剪切模型G12的结果，三种计算方式得到数值相差不大，其中MSG 模型和MMP 模型两者的误差仅为-0.19%和-0.24%，说明MSG在进行蜂窝结构等效弹性模量预测时具有较好的正确性。与代表体元法相比，MSG不用反复施加边界条件，也不必施加周期性边界条件，对于给定尺寸参数的模型一次性即可得到正交各向异性结构的9个弹性等效参数。

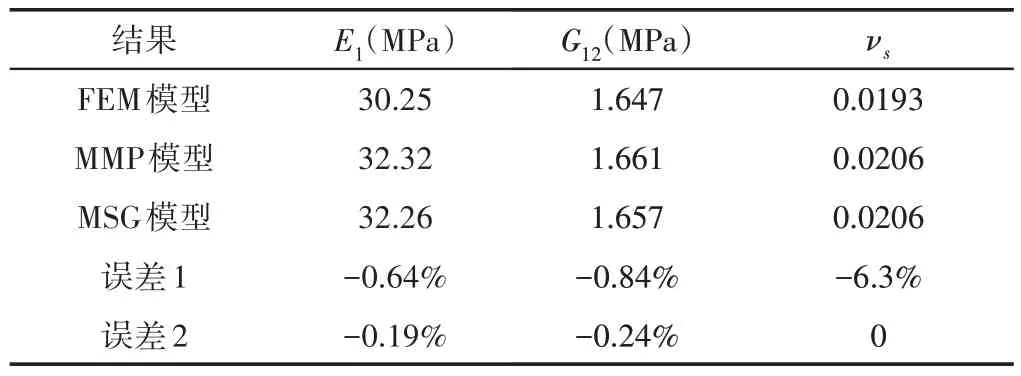
表2 面内杨氏模量试验、有限元和MSG对比Tab.2 Comparison of the Experimental,FEM and MSG Results for the In-Plane Modulus

4.2 蜂窝结构参数对等效弹性参数的影响

在不同的蜂窝壁横斜比β与厚度比γ下，蜂窝结构的等效弹性参数随着角度Φ的变化情况，如图3、图4所示。从图3（a）和图4（a）中可以看出，随着夹角Φ的增加，结构的面内泊松比ν12逐渐降低之后会稳定在0.02附近。这是由于夹角Φ值变大后，受力方向上蜂窝壁是变形的主要区域，垂直于受力方向的蜂窝壁的变形主要是通过两个方向交叉区域而引起的微小横向变形，进而由于垂直于受力方向上蜂窝壁自身材料正泊松比特性造成了蜂窝结构呈现出较小的非零值，如图3（b）、图4（c）所示。当夹角Φ处于（0～15）°范围之间变化时，对结构相对密度的影响较小，随着夹角Φ逐渐增加，达到（15～30）°区间时，结构的相对密度会略有上升。

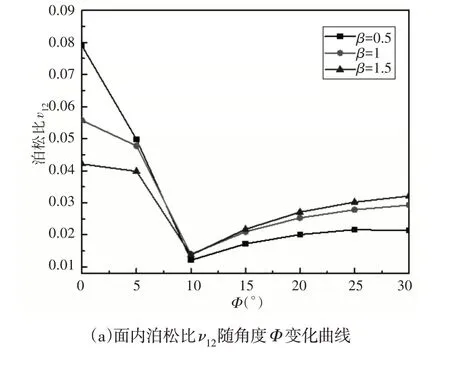
图3 在α=1，γ=0.1时，不同β参数下蜂窝结构等效弹性参数MSG预测值Fig.3 MSG Predictions of the Equivalent Elastic Modulus of the Honeycomb Structure for Various Parameters β while α=1，γ=0.1

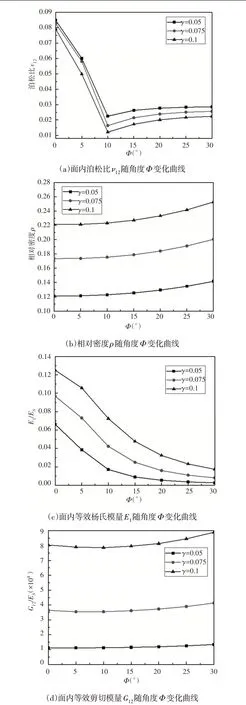
图4 在α=1，β=0.5时，不同γ参数下蜂窝结构等效弹性参数MSG预测值Fig.4 MSG Predictions of the Equivalent Elastic Modulus of the Honeycomb Structure for Various Parameters γ while α=1，β=0.5

在参数β和γ不同的情况下，蜂窝结构的面内杨氏模量会随着夹角Φ的增加而降低，如图3（c）、图4（c）所示。与原材料的模量相比较，蜂窝结构的面内杨氏模量会降低（1～2）个数量级。较低的面内杨氏模量可以使得结构在相同驱动力的条件下，获得更大的变形。

在参数β和γ不变的情况下，夹角Φ对于蜂窝结构的面内剪切模量影响较小，但是根据实际的需求，通过不同的β和γ组合可以使结构得到不同的剪切模量，如图3（d）、图4（d）所示。例如，当β=1.5，γ=0.05时，这种组合会使结构的面内剪切模量最小。蜂窝结构在变体结构中的主要应用是作为蒙皮的支撑结构，支撑结构主要的变形方式是弯曲变形，较低的面内剪切模量会使得支撑结构在一定驱动力的条件下，实现更大的面内弯曲变形。

4.3 新型蜂窝结构与四角星形蜂窝结构对比

当新型蜂窝结构和四角星形蜂窝结构相对密度为0.22时，分析线弹性范围内新型蜂窝结构和四角星形蜂窝结构在不同夹角Φ时面内泊松比的变化情况，从图5（a）中可以看出，相对于四角星形蜂窝结构，新型蜂窝结构的面内泊松比呈现出的零泊松比特性更加稳定。在相同相对密度条件下，对比新型蜂窝结构和四角星形蜂窝结构在夹角Φ=30°的等效弹性模量，如图5（b）所示。此时，新型蜂窝结构的等效面内模量E1小于四角星形结构，二者的剪切模量几乎相等，而前者的面外剪切模量略大于后者。综合对比结果，可以得出新型蜂窝结构不仅保持了原有四角星形结构零泊松比特性，而且该结构的面内变形能力以及抵抗面外变形的能力优于四角星形蜂窝结构。

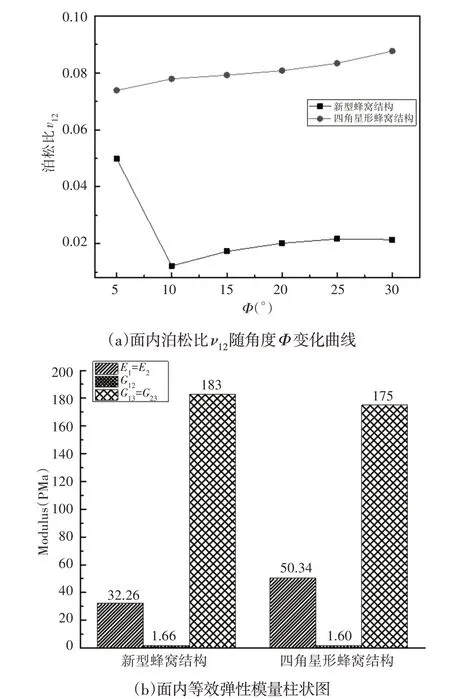
图5 两种蜂窝结构的面内泊松比及等效弹性模量对比Fig.5 Comparison of in-Plane Poisson’s Ratio and Equivalent Elastic Modulus of Two Honeycomb Structures

5 结论

（1）提出了一种新型零泊松比蜂窝结构，该蜂窝结构不仅具有零泊松比特性，而且可以实现面内与面外力学性能的分别设计。通过与四角星形蜂窝结构对比，表明了在同样相对密度条件下，新型蜂窝结构会得到更小的面内模量，而较低的模量可以使得结构在相同驱动力的条件下获得更大的变形，新型蜂窝结构具有在变体飞机柔性蒙皮上的应用前景。

（2）采用一种新的多尺度分析方法-结构基因力学（MSG）分析了等效弹性模量与蜂窝结构几何尺寸参数变化的关系，并结合精细化模型有限元方法验证了该方法的有效性，说明MSG在进行蜂窝结构等效弹性模量预测时具备较好的正确性。

（3）新型蜂窝结构的面内等效弹性模量会随着蜂窝夹角θ、水平壁H和倾斜壁L的增加而降低，同时与原材料的模量相比较，新型蜂窝结构的面内模量会降低（1～2）个数量级。

由于新型蜂窝结构改变了点对点的连接方式，除3D打印工艺外可以采用其他成型工艺，例如采用嵌锁组装工艺结合树脂基复合材料制备新型蜂窝结构，可以在材料层次进一步提升结构可设计性。