基于ISOA的微织构机床伺服前馈补偿控制

王忠明，吴国庆，茅靖峰，胡 坤

（南通大学电气工程学院，江苏 南通 226019）

1 引言

为了进一步满足现代机床加工业的技术需求，机床加工必然朝着高速化和精密化方向发展。微织构机床凭借其可以精确的加工出复杂微观形貌结构，并满足快速定位系统的技术要求，因此被广泛应用于机床加工领域。伺服系统和滚珠丝杠进给系统构成了微织构机床伺服进给系统，而伺服系统的性能影响着微织构机床的速度跟踪精度[1-3]。在设计伺服系统的进程中，PID控制器凭借其适用性强和简单易实现的特点，广泛应用于实际使用中[4]。然而PID参数整定困难成为科研一大难点，随着智能算法研究的不断深入，人们开始将其应用于PID参数寻优中。文献[5]为了解决系统阶跃响应超调以及振荡的问题，提出使用人群搜索优化算法进行参数整定，提高系统的控制精度；文献[6]针对微织构机床位置跟踪精度不高的问题，建立微织构机床伺服传动系统数学模型，采用前馈与反馈结合的改进方法，提高了机床的位置跟踪精度；文献[7]针对水泵系统控制精度不高的问题，使用人群搜索优化算法获得良好的PID参数自整定效果，提高了灌溉系统的运行稳定性。

综上所述，为了进一步提高微织构机床速度伺服跟踪精度，在建立机电耦合动力学模型的基础上，提出基于改进人群搜索优化算法的前馈PID 控制策略，实现微织构机床伺服进给系统的PID参数寻优设计。为验证该控制策略的实际效果，采用Matlab搭建仿真实验平台，与传统智能优化算法相比较。仿真结果表明，基于ISOA优化的前馈补偿PID优化效果更好，速度跟踪性能得到很大改善，验证了其正确有效性。

2 微织构机床伺服进给系统建模

2.1 交流永磁同步电机数学模型

永磁同步电机假设为理想电机：涡流损耗被忽略；永磁体也无阻尼作用；电机阻尼绕组等效于d、q轴上两个短路的阻尼绕组。建立坐标的等效变换，根据矢量控制原理，进而得到d-q坐标系数学模型[8]，其矢量图模型，如图1所示。

图1 永磁同步电机矢量图Fig.1 Permanent Magnet Synchronous Motor Vector

由图1可得出其d-q轴上电压平衡方程式为：

式中：R—等效电阻值；Lq=Ld—dq轴电感；ωr—电机输出轴转子角速度；id、iq—dq轴电流；ud、uq—dq轴电压；pn—磁极对数；φf—永磁体上恒定磁通。

根据式（1）可推导出PMSM的电流方程为：

PMSM的电磁转矩Te为[9]：

2.2 滚珠丝杠进给系统建模

滚珠丝杠与伺服电机通过联轴器相连在一起，滚珠丝杠通过两端的轴承支撑，工作台由滚珠丝杠螺母旋转驱动，沿着直线导轨副做直线往复运动，光栅尺作为负反馈装置，构成系统全闭环，其模型[10]，如图2所示。

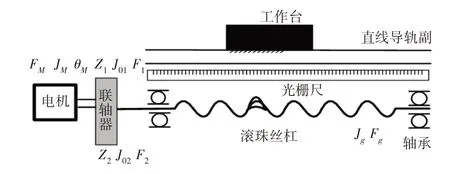
图2 滚珠丝杠进给机构模型Fig.2 Ball Screw Feed Mechanism Model

式中：TL—扰动；J—转动惯量之和，可由等效转动惯量Jo1、Jo2、丝杠转动惯量Jg和电机轴转动惯量JM求出；F—总的阻尼系数，可由电机轴的阻尼FM、滚珠丝杠阻尼Fg和丝杠与电机间等效阻尼F1、F2求出；Z1∕Z2—折算比。

2.3 机电耦合动力学模型

在假设理想电机的条件下，使Ld=Lq=L，FM=0，为了实现快速调速，采用id=0方法用于控制PMSM调速系统定子电流解耦，完全解耦的微织构机床伺服进给系统状态方程为：

根据式（5）的状态方程，微织构机床伺服进给系统框图可描述，如图3所示。

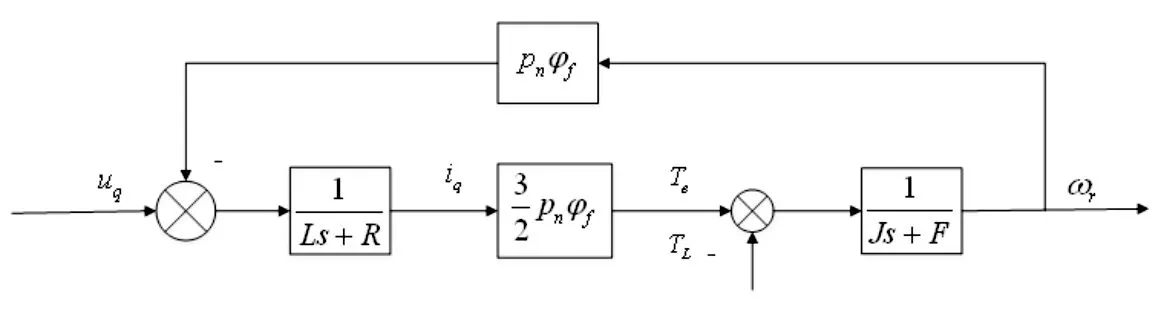
图3 微织构机床伺服进给系统框图Fig.3 Block Diagram of the Servo Feed System for Micro-Texture Machine Tools

根据图3，微织构机床伺服进给系统传递函数GM(s)为：

3 进给系统线性控制器设计

3.1 PID控制

微织构机床伺服进给系统所采用的传统PID控制器，主要是对三个环节参数Ki、Kp、Kd整定，PID控制器框图，如图4所示。

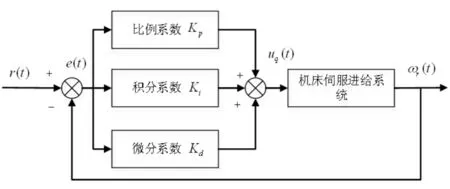
图4 PID控制器框图Fig.4 PID Controller Block Diagram

其控制规律表示为：

式中：e(t)—速度跟踪误差；Ti、Td—积分时间常数和微分时间常数。

3.2 前馈补偿控制器设计

考虑到传统PID控制的反馈控制环节存在延时问题，这些问题会造成控制滞后甚至失效，因此提出前馈补偿的PID 控制方式。其原理框图，如图5所示。

图5 前馈PID控制器框图Fig.5 Feedforward PID Controller Block Diagram

系统传递函数ωr(s)∕r(s)和系统误差关于输入的传递函数e(s)∕r(s)为：

式中：r(s)—初始输入的信号；uq(s)—拉氏变换下的电压输入；GPID(s)—拉氏变换下PID传递函数；e(s)—拉氏变换下的速度跟踪误差；Kf1、Kf2—前馈增益系数。

由上式得可知，当f1(s)+f2(s)=1∕GM(s)时，理论上可消除系统误差。尽管在实际使用中无法完全消除系统误差，但可以将其降低到可接受的水平，尽可能不影响系统稳定性的前提下，机床速度伺服跟踪精度得到很大提升。

对于PID采样周期Tc较短的情况，可通过PID离散化处理，直接将连续系统转换离散系统，因此前馈补偿PID离散控制律可表示为：

式中：e(k)—速度跟踪误差。

对于一个存在非线性和滞后性的微织构机床伺服进给系统，结构简单易实现的PID控制器调参困难成为难题，因此采用改进的人群搜索优化算法的PID参数自整定，来实现系统全局最优控制。

4 人群搜索算法及其改进

4.1 PID控制

人群搜索算法[11]是一种新型人类种群行为的智能算法，把搜索行为的集和当作初始种群，行为个体作为个体解，对位置和方向推理判断是通过人类在进行搜索时的模拟，实现所求问题的最优求解。

使用时间积分的绝对值来构造目标函数，以期得到合适的动态迭代特性，构造的目标函数f为：

人群搜索优化算法遵循人群搜索规则，利用Fuzzy系统的逼近功能，可得到搜索步长αfj关系式为：

式中：ψfj—隶属度函数的参数；

ϖfj—搜索空间目标函数的隶属度。

通过对预动方向de、利他方向da和利己方向dp的理性分析，得出搜索方向df为：

式中：sign()—符号函数；m1、m2—[0，1] 区间随机实数。

得到搜索步长αfj和搜索方向df后，再进行个体位置更新，得到更新后的位置xfj(t+1)为：

4.2 改进的SOA算法

为了解决人群搜索算法在前期搜索效率低以及后期搜索陷入局部极值而无法求出全局最优解的问题[12]，提出了混沌初始化优化策略，并且引入cauchy变异算子，Logistic混沌映射函数反复迭代[13-14]：

模拟试块注浆试验结束后，在顶面位置和侧面位置各取一组芯样(6块)，并对其芯样进行抗压试验。由于试验1的注浆固结效果较差，浆液扩散不均匀导致脱模后完整性差，无法取芯，故只对试验2—试验4进行取芯和单轴抗压强度试验。代表性试样及单轴压缩试验见图5，不同模拟试验方案下的试样取样部位及其单轴抗压强度值见表2。

式中：Φ—迭代次数；μ—调节参数。

在(0，1) 区间内随机产生一个H维的基准粒子y0，y0=(y01，y02，y03···y0H)，产生混沌种群集合yn+1，j为：

接着将式(0，1) 映射到搜寻空间[-Γ，Γ]中，得到H维粒子种群xn+1，j为：

式中：n=0，1，2，···，N，j=1，2，···，H。

为了解决搜索后期陷入局部极值的现象，引入cauchy变异算子，柯西分布的主要表现为其分布函数拥有较长的两翼，其生成的随机数的变异范围更广，因此柯西变异算子增大的变异范围使改进算法拥有更广的搜索范围。

柯西变异的计算公式为［15-16］：

式中：p—随机变异率；

cauchy()—准柯西分布函数。

接着使用柯西分布对Gbest执行变异操作为：

式中：r—变异权重；Gbestj—全局最优第j维分量；λ—常数10；A()—柯西分布最初产生的随机数。

5 基于ISOA算法的前馈控制器设计

5.1 ISOA-PID控制器原理图

利用基于ISOA的前馈补偿PID控制策略，对输出速度跟踪值及其误差值分别进行优化处理，调节控制器的三个参数Kp、Ki、Kd，提高速度跟踪精度，消除速度跟踪误差，到其控制系统原理，如图6所示。

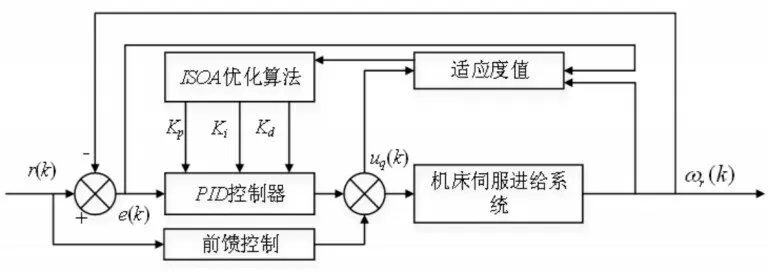
图6 控制系统原理框图Fig.6 Block Diagram of the Control System

5.2 ISOA-PID的算法流程

ISOA优化PID参数流程图，如图7所示。

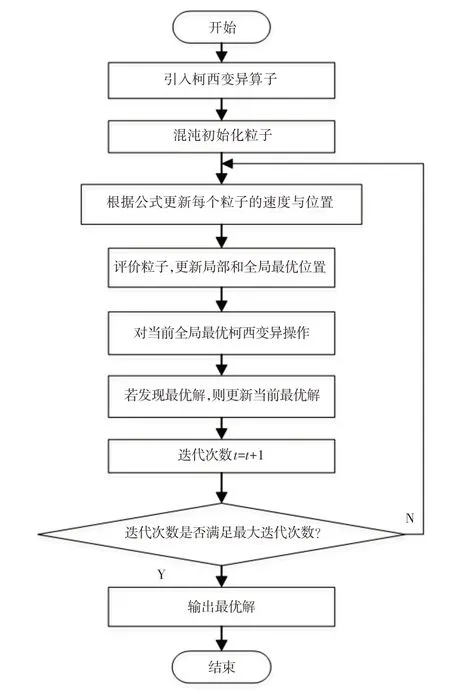
图7 ISOA优化PID参数流程图Fig.7 Flow Chart of ISOA Optimization PID Parameters

6 仿真测试与结果分析

为了验证ISOA+前馈PID算法的正确有效性，设计耦合模型参数，得出微织构机床伺服进给系统传递函数，基于MATLAB仿真与人群搜索优化（SOA）、粒子群优化算法（PSO）和遗传优化算法（GA）进行结果对比。建模所需参数，如表1所示。

表1 机电耦合模型参数Tab.1 Parameters of Electromechanical Coupling Model

微织构机床伺服进给系统传递函数为：

针对微织构机床伺服进给系统数学模型进行仿真研究，分别编写基于ISOA、SOA、PSO和GA优化算法程序，设置起始种群为30，维数为3，采样周期为1ms，最大迭代次数为100代，隶属度最小值为0.0111，隶属度峰值为0.9500，最小权重值为0.1，权重峰值为0.9，四种优化算法仿真Kp、Ki、Kd参数，如表2所示。仿真得到SOA、GA、ISOA和PSO控制适应度值函数控制构制曲线，如图8所示。四种算法的迭代次数和最优适应度值，如表3所示。

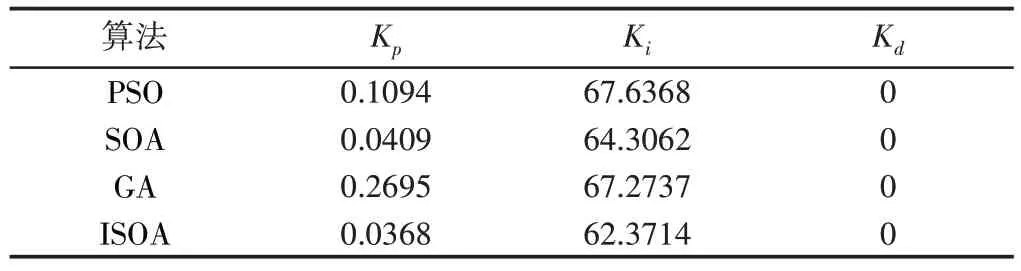
表2 四种优化算法仿真Kp、Ki和Kd参数Tab.2 Four Kinds of Optimization Algorithm Simulation Kp、Ki and Kd Parameters

表3 四种算法的迭代次数与最优适应度表Tab.3 The Number of Iterations and Optimal Fitness of the Algorithms

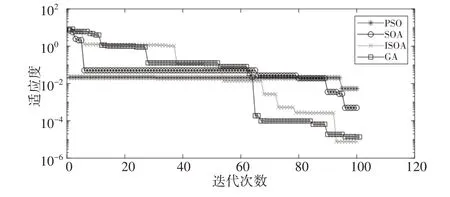
图8 适应度函数控制曲线Fig.8 Fitness Function Control Curve

PSO优化算法经过3次迭代获得的最优适应度值最差且为5.3×10-3，SOA优化算法经过10次迭代获得其适应度函数的最优适应度为4.9742×10-4，GA优化算法经过21次迭代找到的最优适应度为7.6817×10-5，而ISOA 优化算法找到的最优适应度为1.3618×10-6，且仅需要12次迭代。由此可见，四种优化算法相比较，PSO优化算法稳定性最差，而ISOA优化算法在寻找最优适应度值速度最快且最稳定,如表2、图8所示。

将式(19)作为仿真的基础，输入为r=0.5 sin(2πt)的正弦加速度信号，接着使用6种算法仿真，正弦响应速度跟踪曲线，如图9所示。正弦响应速度跟踪误差曲线，如图10所示。分别将正弦响应速度跟踪曲线和正弦响应速度跟踪误差曲线进行局放大，使改进方法与传统优化算法的比对能更清楚直观的表达，正弦响应速度跟踪曲线部分放大图，如图11所示。正弦响应速度跟踪误差曲线部分放大图，如图12、图13所示。

图9 正弦响应速度跟踪曲线Fig.9 Sinusoidal Response Speed Tracking Curve

图10 正弦响应速度跟踪误差曲线Fig.10 Sine Response Velocity Tracking Error Curve

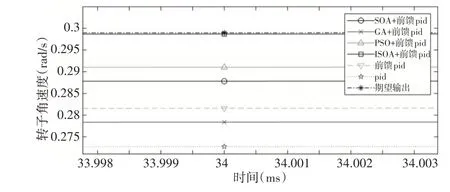
图11 正弦响应速度跟踪曲线部分放大图Fig.11 Partial Enlarged View of the Sine Response Speed Tracking Curve

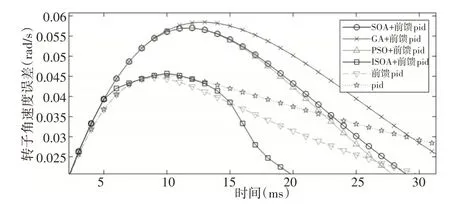
图12 正弦响应速度跟踪误差曲线部分放大图Fig.12 Partial Enlarged View of Sine Response Velocity Tracking Error Curve

图13 正弦响应速度跟踪误差曲线部分放大图Fig.13 Partial Enlarged View of Sine Response Velocity Tracking Error Curve

由图11可知，6种算法中，ISOA+前馈补偿PID 速度伺服跟踪效果最佳，跟踪精度较高，而常规PID跟踪精度最差。由图12所知，在6种算法中，GA+前馈PID误差峰值最大且为0.058rad∕s，而ISOA+前馈PID 误差峰值最小且为0.046rad∕s。由图13所示，ISOA+前馈补偿PID 方法调节最快，0.06s 达到稳定状态，其次PSO+前馈补偿PID方法0.08s达到稳态，其他算法速度跟踪性能略差。综上所述，对于大多数非线性带有迟滞环节系统，微织构机床伺服运动控制系统基于ISOA优化的前馈补偿PID控制效果最优。

7 结论

（1）基于ISOA算法优化的前馈补偿PID控制在微织构机床伺服进给控制中调节时间最短，速度伺服跟踪精确，动态响应特性较好，通过该改进方法可以实现微织构机床伺服进给系统中的最佳控制策略。

（2）在ISOA 算法的使用过程中，调整其适应度函数值和粒子种群的大小能够改善PID参数优化效果，很大程度消除PID控制器在微织构机床伺服进给系统中存在的非线性、时变性和滞后性问题；前馈补偿作为延时系统中常用的模型控制方法，该方法在尽可能不影响系统稳定性的前提下，获得更好的动态特性和更高的控制精度。

（3）仿真结果表明，基于ISOA 的微织构机床前馈伺服控制可以很好的满足机床伺服进给系统的自动控制要求，可应用于实际工业机床控制中。