超晶格插入层对InGaN/GaN多量子阱的应变调制作用*

曹文彧 张雅婷 魏彦锋 朱丽娟 徐可 颜家圣 周书星3)† 胡晓东

1) (湖北文理学院物理与电子工程学院,低维光电材料与器件湖北省重点实验室,襄阳 441053)

2) (湖北台基半导体股份有限公司,大功率半导体技术湖北省重点实验室,襄阳 441021)

3) (武汉大学,电子制造与封装集成湖北省重点实验室,武汉 430072)

4) (北京大学物理学院,人工微结构和介观物理国家重点实验室,北京 100871)

在InGaN/GaN 异质结构量子阱内存在巨大的压电极化场,这严重地削弱了量子阱的发光效率.为了减弱量子阱内的压电极化场,通常引入应变调制插入层提升器件的发光性能.为了研究InGaN/GaN 超晶格的应变调制效果和机理,实验设计制备了具有n 型InGaN/GaN 超晶格插入层的外延结构及其对照样品.变温光致发光谱测试表明引入n 型InGaN/GaN 超晶格插入层的样品发光波长更短且内量子效率提升,相应的电致发光谱积分强度也显著增加且半宽减小,说明引入超晶格应变插入层可以在一定程度上抑制影响发光效率的量子限制Stark 效应.理论计算结果表明: 在生长有源区量子阱前引入超晶格应变层,可以削弱有源区量子阱内极化内建电场,减弱有源区量子阱能带倾斜,增加电子空穴波函数交叠,提高发射几率,缩短辐射复合寿命,有利于辐射复合与非辐射复合的竞争,实现更高的复合效率,从而提高发光强度.本文从实验和理论两方面验证了超晶格应变调制插入层可以有效改善器件性能,为器件的结构设计优化指明方向.

1 引言

第三代半导体器件在节能减排、智能制造、信息安全等国家重点战略领域具有重要意义,现已成为当前国际半导体技术和产业竞争的焦点.十四五规划和2035 年远景目标纲要,特别提出要发展氮化镓(GaN)、碳化硅(SiC)等第三代宽禁带半导体关键技术.GaN 基材料具有化学性质稳定、硬度大、热导率高、耐腐蚀以及抗辐射等特点,在光电子和微电子领域中具有十分广阔的应用前景.其中GaN 基量子阱激光器和发光二极管是固态照明和显示行业发展的前沿方向和研究热点,而由于GaN 基量子阱是具有强极化、高应变的异质量子结构体系,加之具有较高缺陷密度等因素,使得InGaN/GaN 量子阱的研究涉及诸多复杂的物理过程和科学问题.关于如何优化器件结构,提高晶体生长质量,提升发光效率等问题,都直接涉及到器件的可靠性和使用寿命.

InGaN/GaN 多量子阱(multiple quantum well,MQW)有源区结构是GaN 基发光器件的核心结构,是决定其发光效率和工作性能的关键,研究量子阱发光过程的物理机制非常重要,两种主要的机制影响InGaN/GaN 多量子阱器件的发光特性:1)由于In 组分的涨落变化或者相分离,InGaN/GaN 量子阱的阱中形成的类似量子点的结构产生局域态,导致激子局域化[1,2].而大量的局域化激子的存在会抑制非辐射复合,这使发光效率得到提高.2)由于InGaN 的晶格常数大于GaN 的晶格常数,InGaN 量子阱层受到压应力的作用,存在较大的压电极化场[3],这种压电场的存在将导致能带倾斜,使得电子空穴波函数的空间分布发生分离,引起载流子辐射复合几率下降,发光峰值红移,这被称为量子限制Stark 效应(quantum confined Stark effect,QCSE),该效应会加剧俄歇复合和电子泄漏,降低有源区的电光转换效率,是妨碍器件发光效率提升的关键因素之一.从应力调制的角度出发减小QCSE,国内外研究人员进行了很多相关研究[4-7].由于超晶格的特殊结构,能释放外延层中不同材料之间的应力,对削弱多量子阱器件中的极化电场具有重要作用,从而提升器件性能.Li 等[8]在高In 组分黄光InGaN/GaN MQW 结构中采用组分渐变超晶格(superlattice,SL)作为预应变结构,实验结果表明光致发光谱半高宽减小,载流子非辐射复合寿命增加,晶体质量提高;Cai 等[9]利用InGaN/GaN 超晶格代替GaN 作为量子垒,减弱了有源区内的极化电场,提高了空穴在量子阱区中的注入和传输效率,改善了器件的光电性能;邢艳辉等[10]通过在多量子阱下方引入5 个周期的n 型InGaN(2 nm)/GaN(3 nm)超晶格层,缓解了量子阱有源区中的应力,V 型缺陷密度降低约为一半,改善了有源区的表面形貌,多量子阱的光致发光强度提升了43.8%;Shi 等[11]发现与InGaN 单层插入结构相比,InGaN/GaN 超晶格应力调制结构更有效地减小了InGaN/GaN MQW 中的应力,提高了表面形貌.齐维靖等[12]分析了不同超晶格厚度对Si 衬底蓝光发光二极管(light-emitting diode,LED)光电性能的影响,超晶格厚度增加有利于减小量子阱所受的应力,但超晶格厚度大的样品具有更大V 形坑密度,使反向漏电流加剧.目前,对于超晶格应力调制结构的相关理论研究很少,在InGaN/GaN 多量子阱结构中的应用也有待深入研究.本文从实验上测试分析了InGaN/GaN超晶格对InGaN/GaN 多量子阱发光效率的提升效果,并采用Crosslight 器件仿真软件对超晶格插入层的应变调控作用机理进行了深入分析研究.

2 样品制备与表征测试

2.1 样品制备

金属有机化学气相外延(metal organic chemical vapor deposition,MOCVD)技术是如今已经十分成熟的半导体薄膜外延生长技术,广泛应用在光电子器件的研发和产业化生产.MOCVD 技术具有较快的生长速率,能在纳米尺度上精确控制外延层的厚度、组分、掺杂及异质结界面.实验选用Thomas Swan 公司的MOCVD 生长系统来进行InGaN/GaN 多量子阱结构的外延生长.外延结构采用蓝宝石衬底,通过MOCVD 方法沿c轴方向([0001]方向)进行晶体生长.具体结构如图1 所示,依次生长了1 μm 的非掺GaN 缓冲层,3 μm厚的n 型GaN 层.之后是5 个周期的InGaN/GaN量子阱,其中量子阱的阱宽为2.5 nm,势垒宽度为15 nm,平均In 组分约为11%.在量子阱之上最后再生长一层厚度为60 nm 的掺Mg 的P 型GaN.为了研究超晶格结构对于MQW 发光性能的影响,生长了两组样品.从结构上看,传统结构样品由5 个量子阱组成,如图1(a)所示.对于超晶格插入层结构样品,在5 个量子阱与n 型GaN 之间生长了3 个周期的n 型InxGa1-xN(5 nm)/GaN(5 nm)超晶格,总厚度为30 nm,设计In 组分x约为3%,如图1(b)所示.

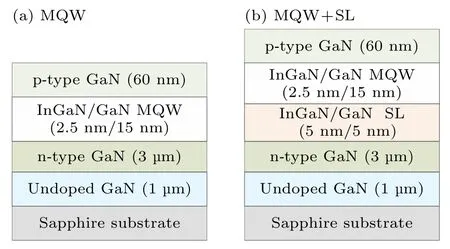
图1 器件外延结构示意图 (a) 传统MQW 结构;(b) 超晶格应变层MQW 结构Fig.1.Schematic diagram of the device epitaxial structure:(a) Traditional MQW structure;(b) MQW structure with a superlattice interlayer.

2.2 表征测试

为了表征多量子阱外延片的发光性质,对两种样品在同等条件下进行了变温光致发光(photoluminescence,PL)的实验,利用波长为325 nm(光子能量约为3.81 eV)的He-Cd 连续激光器来进行光激发,功率为20 mW.用聚焦后的激光对光刻胶进行曝光,并用台阶仪对光斑的大小进行扫描,得到激光束聚焦的光斑面积约0.04 mm2.激光功率密度为50 W/cm2.变温测量过程中,样品置于密闭的通过循环压缩氦气制冷的铜样品座上,样品空间保持真空,利用自动控温装置来准确控制样品温度,实现温度从10—300 K 的连续变化.电致发光谱 (electroluminescence,EL)测量系统的光路结构与光致发光测量装置类似,主要区别是管芯用银胶固定于热沉上,并采用金线键合工艺实现与外部支架焊盘的连接,利用高稳定度直流电源替代PL 测量中所用的激发光源.

3 实验结果与讨论

实验分别测量了传统MQW 结构和超晶格应变层结构两种样品的变温PL 谱曲线(温度范围10—300 K),如图2 和图3 所示.当温度为10 K时,PL 谱线中主峰分别在419 nm (图2)和393 nm(图3),这是来源于InGaN/GaN 多量子阱有源区的发光,可以注意到除了量子阱的发光峰之外还有GaN 层的发光峰(360 nm 左右的小峰),当温度低于60 K 时在图3 中还可以观察到位于381 nm处的超晶格发光峰.另外由于衬底、GaN 薄膜、空气的折射率差异的影响,形成了法布里-珀罗干涉,InGaN/GaN 量子阱的发光峰中存在很多干涉峰,这也反映出晶体质量较好.温度升高时,非辐射复合逐渐增强,辐射复合减弱,导致PL 谱强度降低,图中由上到下依次对应于从10 K 逐渐增加到300 K 时的变温PL 谱.一般来说,假设低温时发光效率为100%,内量子效率(internal quantum efficiency,IQE)可以定义为300 K 与10 K 的积分PL 强度之比[13],公式如下所示:

图2 传统MQW 结构在不同温度下的光致发光谱.插图为PL 谱积分强度随温度的变化及Arrhenius 拟合曲线Fig.2.PL spectra of the traditional MQW structure at different temperatures.The inset shows the temperature dependence of the integrated PL intensity with the best fitting of the Arrhenius plot.

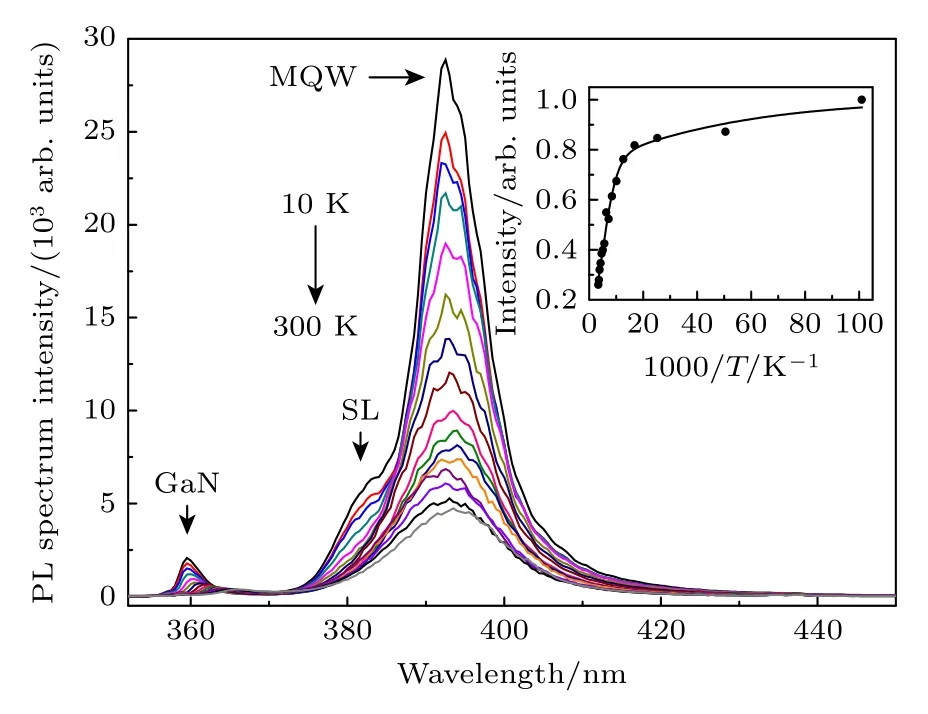
图3 超晶格应变层MQW 结构在不同温度下的光致发光谱.插图为PL 谱积分强度随温度的变化及Arrhenius 拟合曲线Fig.3.PL spectra of the MQW structure with a SL interlayer at different temperatures.The inset shows the temperature dependence of the integrated PL intensity with the best fitting of the Arrhenius plot.

对于传统的多量子阱结构,计算出内量子效率为22%,而对于具有超晶格应变层的多量子阱结构样品其内量子效率为26%.可见具有超晶格应变层结构的量子阱其内量子效率有所提升.

图2 和图3 的插图分别为两样品PL 谱积分强度随温度的变化曲线以及Arrhenius 拟合曲线.利用下面的Arrhenius 公式[14]拟合PL 谱积分强度的数据点:

式中,I(T)代表在温度为T时归一化的积分PL强度;常数α 和β 代表与非辐射复合中心密度有关的速率常数.样品的积分强度在低温段变化较小,而进入高温区域之后快速下降,EA1和EA2分别表示低温和高温区的激活能.其中较低的激活能EA1为局域激子束缚能,较大的激活能EA2为量子阱内的载流子从局域势能最低点跃迁到非辐射复合中心所需跨过的势垒能量.在这四个参数中,最重要的是激活能EA2,它的大小对应于局域化的强度.

拟合参数结果如表1 所列,从α 和β 的比较可以看到,α 的值远小于β,因而对内量子效率影响较大的是激活能EA2,其中超晶格样品的激活能EA2(33.37 meV)比传统样品的EA2(47.80 meV)小.对于传统样品,它的激活能EA2比较大,意味着光生载流子更容易被限制在局域态中辐射发光,而不易跃迁到非辐射复合中心将能量损耗掉,因而通常对应于较长的发光波长及较高的内量子效率[15].但是传统结构内量子效率为22%,而超晶格样品的内量子效率为26%.这说明除局域态的影响之外,压电极化场发挥比较重要的作用.在量子限制斯塔克效应(QCSE)的影响下,应变量子阱中的极化场引起量子阱中的势能倾斜,导致发光效率降低.传统多量子阱结构中存在较强的QCSE 降低了内量子效率,而超晶格应变层结构缓解了QCSE,使之具有较高的内量子效率,对量子阱中的QCSE 状况进行深入分析非常重要.

表1 拟合参数 α,β,EA1,EA2 及内量子效率Table 1.Fitting Parameters of α,β,EA1,and EA2 together with the internal quantum efficiency.

对PL 谱线进行高斯拟合,可以得到InGaN/GaN 多量子阱的发光峰值能量随温度的变化情况.如图4 所示,当温度为10 K 时,应变层结构的PL谱峰值能量为3.15 eV,传统MQW 结构峰值能量为2.96 eV,可见引入超晶格应变层后峰值能量更高,这主要来源于超晶格应变层结构缓解QCSE所引起的峰值蓝移.当温度从10 K 升高到200 K时,传统MQW 结构峰值能量蓝移了45 meV,而在应变层结构中峰值能量蓝移只有16 meV.在量子限制斯塔克效应中,对于理想的宽度为d的无限深势阱,当电场较小时,利用微扰理论,电场造成的n=1 能级的能量红移正比于电场强度ε的平方 ΔE∝-ε2d4,因而有 dE/dε∝-ε,说明当电场减小同样值时,对于本来电场较强的情况会发生更大的能量蓝移.Takamasa Kuroda 等[16]关于InGaN 量子阱中的载流子屏蔽效应进行了理论计算,采用求解泊松方程和薛定谔方程自洽解的方法对不同载流子浓度下的这种峰值移动进行计算,得到非线性的峰值蓝移.图4 中的实验结果可归因于,随温度升高而热激活的载流子,部分屏蔽压电极化场导致的蓝移现象,极化场越强时,这种屏蔽效应越显著,蓝移量越大.相对较小的蓝移量说明引入超晶格应变插入层可以削弱量子阱中极化电场.

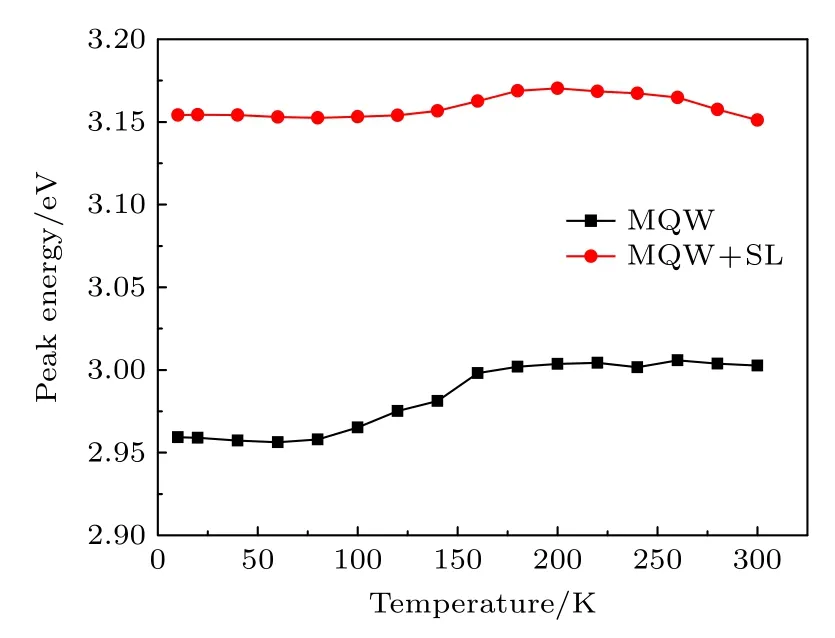
图4 两种MQW 结构PL 谱峰值能量随温度的变化Fig.4.Temperature-dependent variations of PL spectral peak energy for two MQW structures.

为了表征电注入时器件的性能,测量了注入电流100 mA 时两种样品的电致发光谱,如图5 所示.对谱线进行高斯拟合,得到传统结构峰值波长为418 nm,半高宽为23 nm,应变层结构峰值为391 nm,半高宽为16 nm.应变层结构样品的半高宽比传统样品更窄,这主要有两方面原因,加入应变层后生长量子阱相比普通量子阱其阱内具有较小的势能涨落,阱区内非辐射复合中心的数目有效地减少了[17,18].这样生长更均匀、非辐射复合中心更少的量子阱发光峰半高宽会相应减小.另外,应变调制后对QCSE 的抑制增强,使电子空穴波函数重叠的更多,半高宽减小.对比EL 谱线的积分强度,超晶格应变层结构其EL 积分强度相对传统样品提升了8.6%,说明引入超晶格之后多量子阱的发光性能有明显的提高.

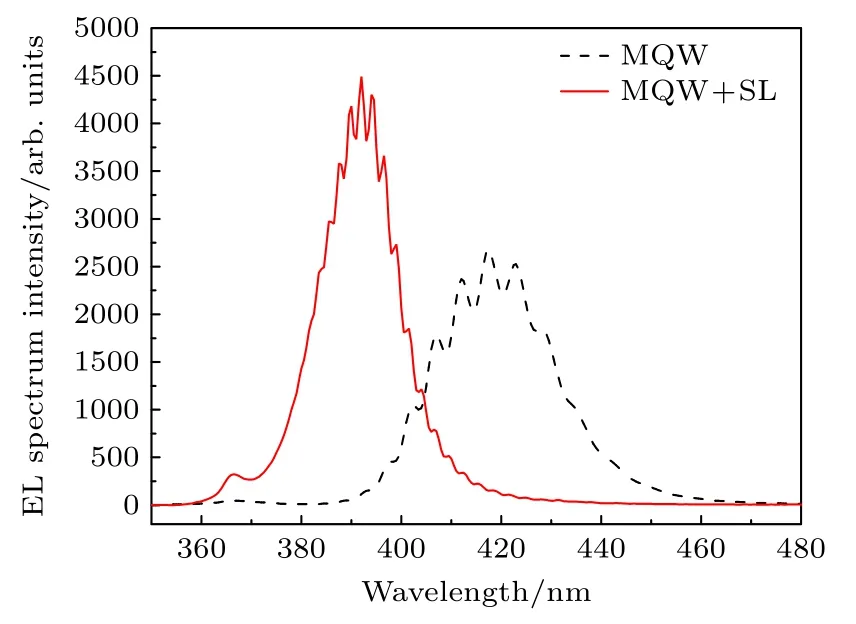
图5 注入电流为100 mA 时两种MQW 结构的电致发光谱Fig.5.EL spectra of two MQW structures at injection current of 100 mA.

为进一步分析发光增强和QCSE 减弱的起源,对量子阱中的压电极化场状况进行深入分析和理论研究非常重要[13].利用加拿大Crosslight 公司提供的APSYS 软件进行器件仿真,采用基于简并微扰论的 k·p 方法计算能带,并借助有限差分方法进行求解,实现了六方结构III 族氮化物体材料和量子阱有源区的能带结构计算.自洽求解模型需要满足相应的物理方程,其中最基本的方程包括:Schrödinger-Poisson 方程和电流连续性方程,并添加漂移-扩散模型[19],界面陷阱俘获模型[20]以及Fiorentini 提出的自发极化和压电极化模型[21,22]等物理模型,使计算结果更加准确.在纤锌矿结构III 族氮化物晶体中,同时存在自发极化和压电极化效应,对于InGaN/GaN 量子阱结构而言,由于阱很薄,可近似认为垒中无应力,应力主要分布在阱区,由于InGaN 的晶格常数比GaN 大,InGaN阱层受的是压应力.在这种情况下,材料中的总极化强度为自发极化强度和压电极化强度之和.对于量子阱的多层平行结构,考虑静电场边界条件,电位移矢量在界面处法向连续,可得

其中εi,Ei和Pi分别为第i层的介电系数,电场强度以及极化强度,下标j代表相邻的第j层相应物理量.另外,考虑到周期性边界条件,多层平行结构的垂直方向上总电压降应为0,因而有

其中li为第i层的厚度.由(3)式和(4)式可以得到多量子阱中第j层中的极化电场为[23]

如果假设电场主要由相邻垒/阱层所影响,(5)式可以简化为

其中,EB和EW分别为垒中和阱中的电场;lB和lW分别为垒层和阱层的厚度.对于多量子阱和超晶格结构,可直接运用以上(5)式—(7)式进行计算.

需要注意的是,在以上的讨论中,晶格的应变都是根据理想情况进行计算的,得出的量子阱中的极化电场通常比实验观察到的要大很多.在实际晶体中,由于界面处悬挂键和其他缺陷的存在,使得量子阱中的应力存在一定程度的释放,因此一般采用计算结果的30%作为实际的极化电场强度[24,25].

在计算前先建立与实际器件结构相近的模型,设计一个具有上下电极的多量子阱结构作为传统结构,以 In0.11Ga0.89N/GaN 量子阱作为有源区,对于SL 插入层结构,模型中有源区结构不变,加入了3 个周期的n 型In0.03Ga0.97N/GaN 超晶格.然后依据文献建议的取值设置器件各层材料参数.P 型层掺杂浓度为1.2×1018cm-3,n 型层掺杂浓度取为5×1018cm-3,分别计算了有无超晶格应变层的InGaN/GaN 多量子阱的能带结构.如图6 所示,当注入电流为100 mA 时模拟计算出的量子阱中能带图,为了区分不同量子阱,最靠近n 型层的量子阱标记为QW1,沿生长方向依次为QW2,QW3,QW4,QW5.根据势能倾斜程度可以计算出量子阱中的电场大小,每个阱中电场强度的模拟结果列在表2 中,以第一个量子阱QW1 为例,传统MQW 结构中电场是442.5 kV/cm,具有超晶格插入层的样品中电场为396.7 kV/cm,其他4 个阱中的电场变化也具有相同的趋势,证明了超晶格应变结构削弱了极化内建电场,抑制了对发光不利的量子限制斯塔克效应,这也与前面实验结果和分析相吻合,即在生长量子阱前加入超晶格应变层可有效缓解应力在量子阱中的分布,使量子阱内的压电极化场随之减小,能带的倾斜程度因此得到减弱,有效带隙变宽,发光波长变短,因而加入超晶格应变层后量子阱的PL 和EL 发光峰值相比传统MQW 结构产生蓝移.

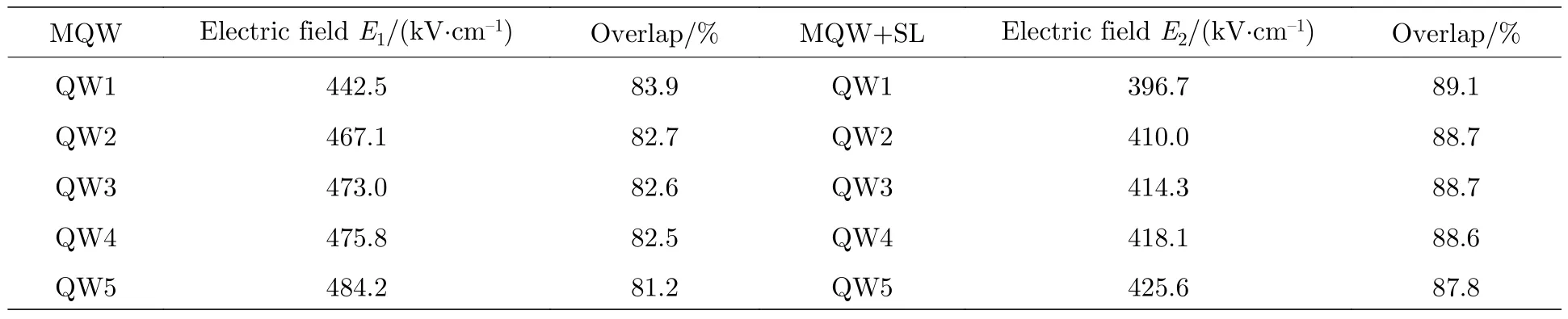
表2 量子阱中电场强度和波函数交叠积分模拟结果Table 2.Simulation results of the electric field and wave function overlaps in each quantum well.

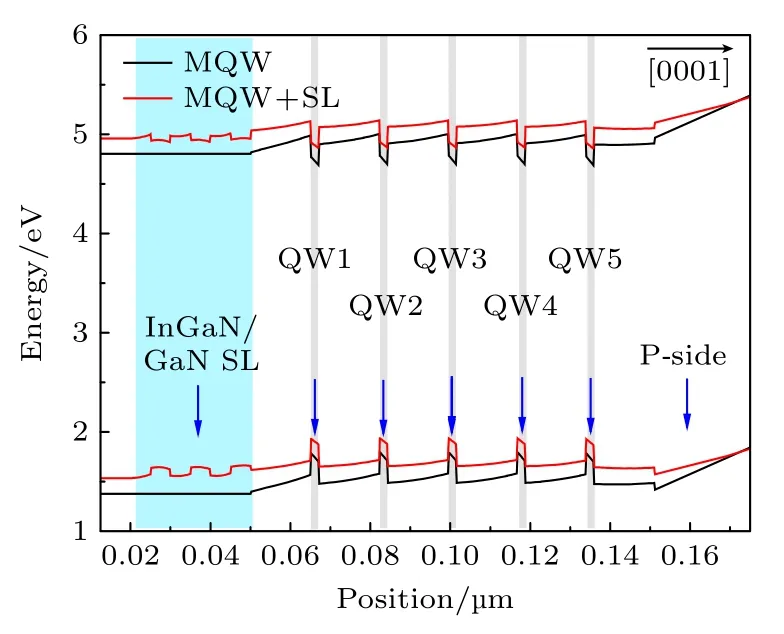
图6 注入电流为100 mA 时两种样品的能带结构Fig.6.Energy band diagrams of two samples at injection current of 100 mA.

由于在辐射复合中,从导带底(C1)能级到价带顶重空穴带(HH1)能级的跃迁起主要作用,我们计算了导带底和价带顶的波函数.图7(a)和图7(b)分别为100 mA 下传统结构和超晶格应变层结构五个量子阱中的电子和空穴波函数空间分布和交叠.因为极化电场的存在,电子和空穴的波函数产生空间偏移,各自聚集在阱区相反的两侧,造成相应的交叠积分减小,直接导致量子阱中相应能级之间的跃迁几率减小.相比于传统MQW 结构,由于超晶格插入层减小了阱中的电场,计算结果表明电子空穴波函数交叠增加,以第一个量子阱QW1 为例,波函数交叠积分从83.9%升高到89.1%.而且表2 所列每个阱中的波函数交叠都有不同程度的提升.电子空穴波函数交叠的增加意味着更高的光跃迁量子效率[26],缩短了辐射复合寿命,有利于辐射复合与非辐射复合的竞争,在量子阱中实现更高的复合效率可以提高发光强度,这与上文实验中观察到的,在100 mA 注入电流下,超晶格应变层结构EL 发光强度提高了8.6%相符.

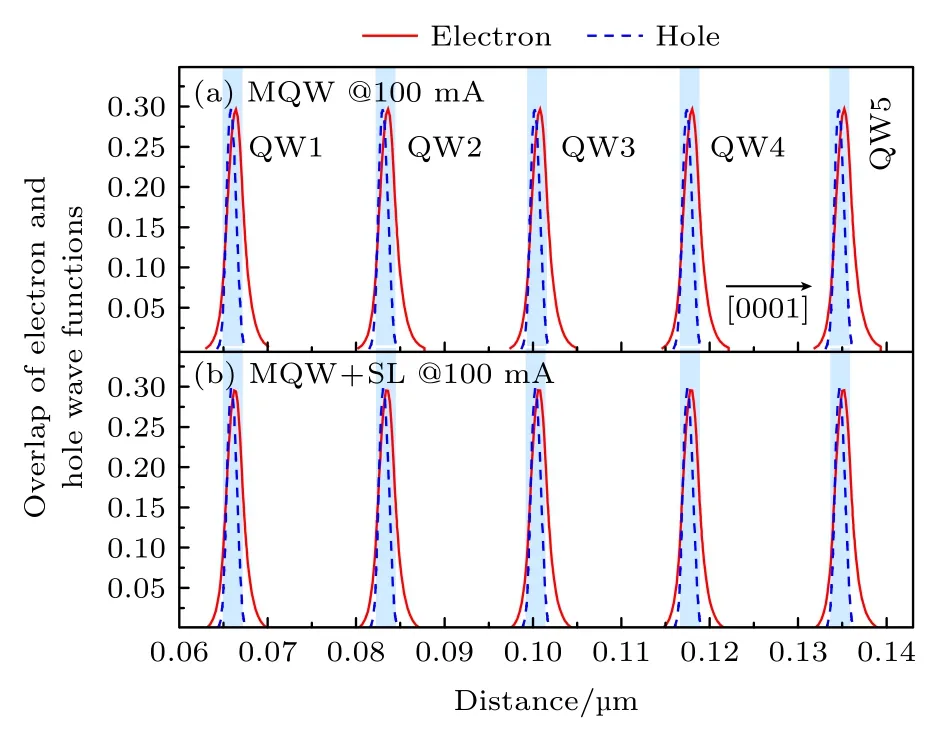
图7 注入电流为100 mA 时,MQW 结构(a)和超晶格应变层MQW 结构(b)五个量子阱中电子空穴波函数空间分布和交叠Fig.7.Electron and hole wave function distributions and overlaps in the five quantum wells of the MQW structure(a) and MQW structure with a SL interlayer (b) at 100 mA.

4 结论

本文研究了应变调制层对InGaN/GaN 多量子阱发光性能的影响.对于变温PL 谱进行了分析,超晶格应变层MQW 的内量子效率有所提升,电致发光实验表明引入应变结构后EL 峰值积分强度明显增大,这都说明应变层在一定程度上抑制了影响发光效率的QCSE.理论计算表明,这归因于超晶格应变层减小了量子阱内的能带倾斜,削弱了每个量子阱中的压电极化场,促使电子空穴波函数交叠积分增加,从而提升了辐射复合效率,提高器件工作的可靠性,从理论和实验两个方面证明了这种应变调制方法的有效性.