含有非热电子和陷俘离子的复杂等离子体中非线性尘埃声波的传播特征

林麦麦 宋晨光 王明月 陈富艳

(西北师范大学物理与电子工程学院,兰州 730070)

本文研究了同时含有非热(nonthermal)电子和陷俘(trapped)离子分布的复杂等离子体系统中非线性尘埃声波的传播特征.首先,利用线性化方法推导得到非线性尘埃声波的色散关系.接着,借助Sagdeev 势方法推导得到表征非线性尘埃声波运动的二维自治系统、Sagdeev 势方程和Sagdeev 势函数的具体表达式.然后,依据数值模拟的方法分析了多种系统因素对二维自治系统相图的重要影响.结果表明: 含有nonthermal 电子和trapped 离子的复杂等离子体系统中同时存在线性周期波、非线性周期波和孤立波.接下来,通过讨论Sagdeev 势函数随系统参数的变化规律发现: 该复杂等离子体系统中仅存在振幅大于零的压缩型孤立波.最后,探讨多种系统因素对非线性尘埃声孤波的振幅、宽度和波形等传播特征的重要影响.结果显示: 马赫数、nonthermal 电子和trapped 离子以及尘埃颗粒未扰动的数密度、温度及荷电量等参数对该复杂等离子体系统中非线性尘埃声孤波的振幅、宽度和波形等传播特性均具有显著影响,且该结果与Sagdeev 势函数的分析结果保持一致.

1 引言

近年来,复杂等离子体中非线性波动过程的研究已经成为等离子体物理的热门前沿课题之一[1-3].由于复杂等离子体广泛存在于实验室环境、自然界以及星际空间中,因此复杂等离子体的理论研究在天体物理学、核聚变物理学等众多学科领域具有重要的研究价值和实践意义[4-6].复杂等离子体作为由电子、离子、质子以及尘埃颗粒所组成的电离气体系统,存在非线性电子声波、非线性离子声波等多种典型的非线性波动模式.而非线性尘埃声波作为典型的非线性波动模式之一,关于其传播特性的研究则是等离子体物理的重要研究课题之一.众多科研工作者对复杂等离子体中的多种非线性波动过程进行了广泛的研究[7-17],例如1990 年,Rao 等[7]在理论上首次预言了非线性尘埃声波的存在性.1995 年,Barkan 等[8]在实验室中观测到非线性尘埃声波,进而验证了Rao 等[7]预言的准确性.1998年,Xie 等[9]考察了尘埃电荷的存在对尘埃声孤子的影响.2005 年,Lin 和Duan[10]研究了不同尘埃大小分布下含有双温离子的热尘埃等离子体中(2+1)维非线性尘埃声波的波动过程.2019 年,Murad 等[11]考虑了含有superthermal 电子的等离子体系统中非线性尘埃声波的传播特征.2023 年,Mamani[17]研究了含有非热(nonthermal)电子和离子的磁化等离子体中任意振幅的非线性尘埃声波的传播特性.研究表明,在实验室以及空间等离子体环境中,电子与离子的分布形式不一定服从经典的麦克斯韦-玻尔兹曼分布.例如,卫星观测证实,在太阳风、地球磁层、星际介质以及极光区等空间环境中的等离子体所含电子存在nonthermal 分布状态[18-23];太阳中微子中所含的电子则存在nonextensive 分布状态[24];而在地球磁层日侧极光带中的等离子体所含电子则存在vortex-like 分布[25].另一方面,在空间和实验室等离子体中的离子也会呈现多种不同的分布形式,例如在实验室的核聚变装置中的等离子体所含离子存在陷俘(trapped)分布状态[23,26].土星e 环中等离子体所含离子则存在nonthermal 分布[27];而金星电离层的等离子体则存在superthermal 离子分布形式[28].众多研究工作表明: 非经典麦克斯韦-玻尔兹曼分布的电子和离子分布状态,对复杂等离子体中的非线性波动过程存在重要影响.例如,Sabry 等[29]研究了含nonthermal 电子的尘埃声孤波的传播特征,结果表明: 孤立波的振幅随着nonthermal 电子的增加而降低.Amour 与Tribeche[30]研究了具有q-nonextensive 电子速度分布的尘埃声孤波,结果显示: 电子的q-nonextensive 分布状态显著影响了孤立波的波动模式.Haider 等[31]研究发现: vortex-like 电子分布对无碰撞的磁化尘埃等离子体中的孤立波的振幅具有显著影响.Ghai 与Saini[32]研究了双温superthermal 离子对非线性冲击波的影响,发现随着低温superthermal 离子超热性的增加,正激波的振幅减小;而具有高阶非线性修正的激波,其振幅会增大.Annou 等[33]研究表明: nonthermal离子数是表征非磁化尘埃等离子体中尘埃声孤波出现与否的重要参数.Mamun[34]对含有trapped离子的三组分尘埃等离子体中非线性尘埃声波的传播特征的研究表明: 随着trapped 离子数的增加,孤立波的振幅将呈现逐渐增大的趋势.

本文着重讨论多种系统因素对同时含有nonthermal 电子和trapped 离子的复杂等离子体系统中非线性尘埃声孤波传播特性的重要影响.首先,给出了由尘埃颗粒、nonthermal 电子和trapped离子组成的复杂等离子体系统中(1+1)维非线性尘埃声波的理论模型;然后,利用线性化方法分析了非线性尘埃声波的色散关系,并依据Sagdeev 势方法推导得到二维自治系统、Sagdeev 势方程以及Sagdeev 势函数的具体表达式;接下来,借助数值模拟方法,详细讨论了二维自治系统的相图、Sagdeev 势函数以及非线性尘埃声孤波随多种系统参数的变化规律.

2 理论模型

为了研究同时含有nonthermal 电子和trapped 离子的复杂等离子体系统中的非线性尘埃声波的演化特征.假设: 复杂等离子体系统由尘埃颗粒、nonthermal 电子和trapped 离子构成且该系统中的非线性波随一个空间坐标x与一个时间坐标t演化,则该系统中无量纲化的(1+1)维非线性尘埃声波的运动方程具体形式如下[35-37]:

其中尘埃颗粒数密度nd由未扰动的尘埃数密度nd0无量纲化;尘埃颗粒流速ud由Cs=(ZdKBTi/md)1/2无量纲化;静电势ϕ由kBTi/e 无量纲化;空间坐标x由电子德拜半径λD=无量纲化;时间坐标t由尘埃等离子体振荡周期无量纲化,这里Zd是尘埃颗粒的荷电量,KB是玻尔兹曼常数,Ti是离子温度,md是尘埃颗粒质量.参数σd=Td/ZdTi表示尘埃-离子温度之比;δ=ne0/(Zdnd0) 则为未扰动的电子与尘埃数密度之比,其中ne0表示未扰动的电子数密度.此时该系统满足的等离子体准电中性条件为ni0=ne0+Zdnd0.nonthermal 电子分布表示形式如下[38]:

其中,σi=Ti/Te,βe=4α/1+3α.这里Te为电子温度,α表示nonthermal 电子数.trapped 离子分布的具体表达式为[34]

其中γ=4(1-b)/是捕获参数,b为决定trapped 离子数量的参数[39]: 当b=0 时,为flat-topped离子分布状态;当b=1 时,为Boltzmann 分布;当b＜0 或 0＜b＜1 时,则表示trapped 离子分布状态.

利用线性化方法,假设:

可获得非线性尘埃声波的色散关系,

图1 给出了同时含有nonthermal 电子和trapped 离子的复杂等离子体系统中非线性尘埃声波的色散关系在不同参数取值下的变化规律.结果显示: 频率ω随着波矢k和nonthermal 电子α,σi,σd的增大而增大;随着δ的增加而减小.这说明,当复杂等离子体系统中出现nonthermal 电子时,该系统中的非线性尘埃声波将以更高的频率传播;而与此同时,电子和离子的温度、尘埃颗粒的荷电量等系统因素对非线性尘埃声波的传播频率也存在一定影响.

图1 色散关系随不同参数的变化规律Fig.1.Variations of dispersion relation with different parameters.

3 理论推导

接下来,利用Sagdeev 势方法研究同时含有nonthermal 电子和trapped 离子的复杂等离子体系统中非线性尘埃声波的传播特性.首先,对方程(1)—(3)中的自变量进行坐标伸展变换.令ξ=x-Mt,其中M为马赫数,得到以下关系式:

则原方程组(1)—(3)变形为

化简(6)式和(7)式并考虑边界条件[40]:当ξ→±∞时,nd→1,ud→0,ϕ→0,可知

将以上结果代入(8)式可得

其中,

将(9)式转化为二维自治系统:

对(9)式两边同时乘以 dϕ/dξ,并对ξ积分一次,即可得Sagdeev 势方程形式如下:

其中Sagdeev 势函数的具体表达式为

4 数值分析

接下来,利用数值分析的方法探讨多种系统参数,如M,α,b,σi,σd,δ等对复杂等离子体系统非线性动力学行为的影响,以便探究不同的系统参数对同时含有nonthermal 电子和trapped 离子的复杂等离子体系统中非线性尘埃声波的重要影响.

图2 给出了复杂等离子体系统的相图随着不同马赫数M的变化规律,其他系统参数取值分别为[41,42]:α=0.4,b=0.8,σi=0.5,σd=0.02,δ=2 .当马赫数M=1.3,1.4 和1.5 时,含有nonthermal 电子和trapped 离子的复杂等离子体系统中存在一个中心点和鞍点;而且围绕中心点出现线性周期波轨道和非线性周期波轨道;另外,还出现了从鞍点出发回到同一鞍点的同宿轨道[43].这说明该系统同时存在线性周期波解、非线性周期波解和孤立波解.与此同时,图2 还表明: 随着马赫数的增大,线性周期波轨道、非线性周期波轨道和同宿轨道存在的范围将逐渐减小,这说明当系统的马赫数M改变时,将影响线性周期波轨道、非线性周期波轨道和同宿轨道所存在的相空间区域.

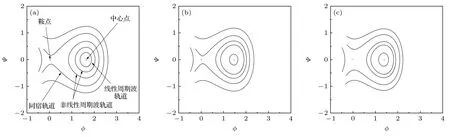
图2 系统相图随马赫数M 的变化 (a) M=1.3;(b) M=1.4;(c) M=1.5Fig.2.Variations of system phase diagram with different M: (a) M=1.3;(b) M=1.4;(c) M=1.5.

图3 给出了二维自治系统的相图随着nonthermal 电子数α的变化规律,其中M=1.3,b=0.8,σi=0.5,σd=0.02,δ=2.图3 的数值模拟结果表明: 在不同的nonthermal 电子数α取值下,复杂等离子体系统仍存在中心点、鞍点及三种不同类型的轨道(线性周期波轨道、非线性周期波轨道和同宿轨道).通过对比图3(a)—(c),不难发现: 虽然相轨道特征会随着nonthermal 电子数α的不同而发生一定变化,但是该系统同时存在线性周期波解、非线性周期波解和孤立波解的基本属性不会改变.这说明在实验室与空间环境中,复杂等离子体中所含的非经典分布状态的nonthermal 电子分布对该系统的非线性尘埃声波的波动模式存在显著影响.

图3 系统相图随nonthermal 电子数 α 的变化 (a) α=0;(b) α=0.4;(c) α=0.8Fig.3.Variations of system phase diagram with different α : (a) α=0;(b) α=0.4;(c) α=0.8.

二维自治系统相图随着trapped 离子数b的变化规律由图4 给出,其中M=1.3,α=0.4,σi=0.5,σd=0.02,δ=2.由数值模拟结果不难看出,当trapped 离子数b从0.7 逐步增加到0.8,0.9 时,该系统仍然同时存在线性周期波解、非线性周期波解和孤立波解,这表明trapped 离子分布状态会直接影响复杂等离子体系统中线性周期波解、非线性周期波解和孤立波解的存在范围.

图4 系统相图随trapped 离子数b 的变化 (a) b=0.7;(b) b=0.8;(c) b=0.9Fig.4.Variations of system phase diagram with different b: (a) b=0.7;(b) b=0.8;(c) b=0.9.

图5 给出了二维自治系统的相图随着参数σi的变化规律,在这里其他系统参数取值分别为:M=1.3,α=0.4,b=0.8,σd=0.02,δ=2.图5显示: 同时含有nonthermal 电子和trapped 离子的复杂等离子体中,系统参数σi会影响同时存在的线性周期波轨道、非线性周期波轨道和同宿轨道的存在范围.考虑到σi=Ti/Te,这说明该复杂等离子体系统中的电子温度、离子温度及电子温度与离子温度之比均会对系统的线性周期波解、非线性周期波解和孤立波解存在一定的影响.

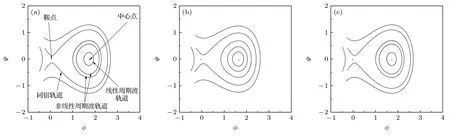
图5 系统相图随参数 σi 的变化 (a) σi=0.4;(b) σi=0.5;(c) σi=0.6Fig.5.Variations of system phase diagram with different σi:(a) σi=0.4;(b) σi=0.5;(c) σi=0.6.

当M=1.3,α=0.4,b=0.8,σi=0.5,δ=2时,二维自治系统的相图随着系统参数σd的变化规律由图6 给出.可以明显看出,当系统参数σd从0.02,0.05 逐步增加到0.08 时,系统相图中不同类型相轨道的存在范围会随着σd的改变而改变.由于σd=Td/ZdTi,这表明: 该复杂等离子体系统的线性周期波解、非线性周期波解和孤立波解的存在范围与尘埃颗粒的温度、荷电量和离子的温度均存在一定联系.

图6 系统相图随参数 σd 的变化 (a) σd=0.02;(b) σd=0.05;(c) σd=0.08Fig.6.Variations of system phase diagram with different σd:(a) σd=0.02;(b) σd=0.05;(c) σd=0.08.

图7 给出了二维自治系统相图随着δ的变化规律,其他系统参数取值分别为:M=1.3,α=0.4,b=0.8,σi=0.5,σd=0.02.数值模拟结果显示:系统参数δ的取值变化,并不会影响该系统中同时存在线性周期波轨道、非线性周期波轨道和同宿轨道的基本特征.但该系统的多种相轨道的存在范围则随着δ的增大而逐渐变小.由于参数δ=ne0/(Zd0nd0),这说明同时含有nonthermal 电子和trapped 离子的复杂等离子体系统中所含电子、离子的未扰动数密度,以及尘埃颗粒数密度、荷电量等重要参数对该系统的线性周期波、非线性周期波和孤立波均存在一定的影响.

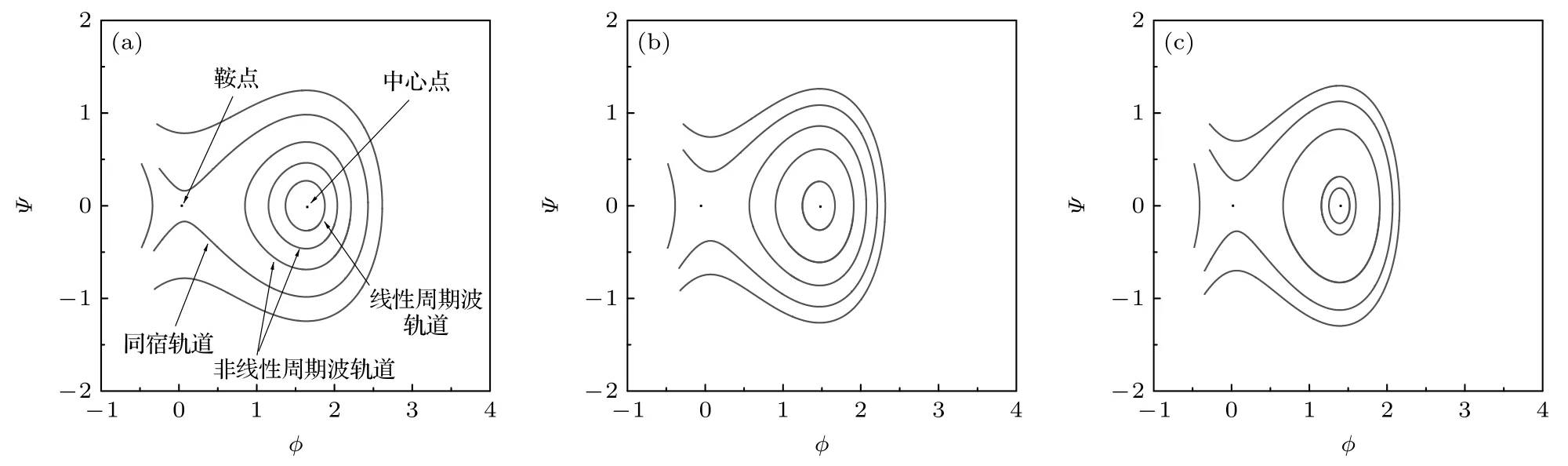
图7 系统相图随参数 δ 的变化 (a) δ=2;(b) δ=3;(c) δ=4Fig.7.Variations of system phase diagram with different δ:(a) δ=2;(b) δ=3;(c) δ=4.

接下来,探讨系统参数对Sagdeev 势函数的影响.研究结果表明[40]: Sagdeev 势函数表征孤立波存在的条件是Sagdeev 势函数满足当ϕ=0 时,V(ϕ)=0,dV/dϕ=0 且 d2V/dϕ2＜0.利用数值模拟分析的方法,可以获得同时含有nonthermal电子和trapped 离子的复杂等离子体系统中的Sagdeev 势函数V(ϕ) 随多种系统参数的变化规律,如图8 所示.结果表明: 在多种不同的系统参数取值下,Sagdeev 势函数V(ϕ) 均存在两个零点,分别为ϕ1=0 和ϕ2=ϕm,且ϕm＞0.这意味着该复杂等离子体系统中仅存在振幅大于零的压缩型孤立波.

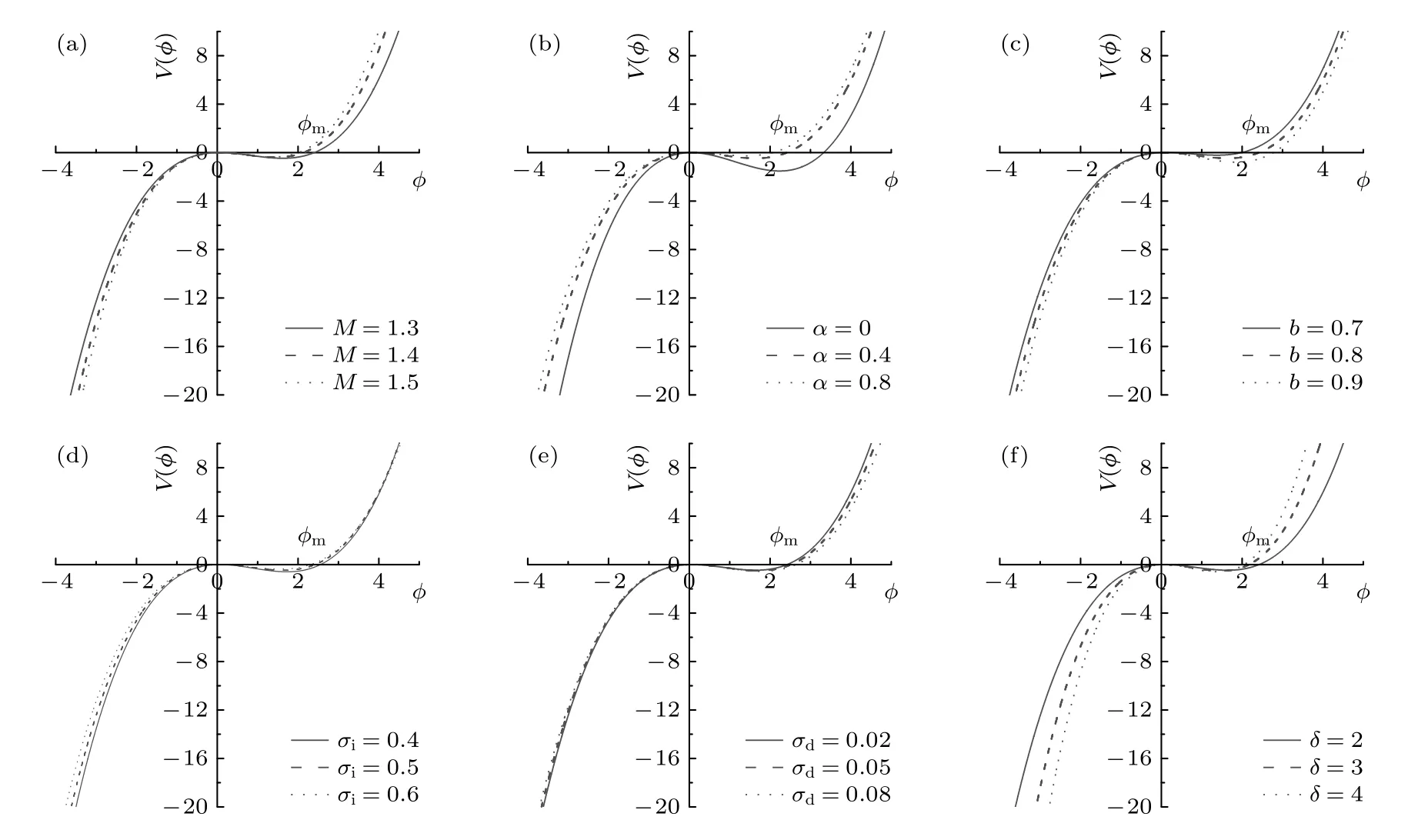
图8 Sagdeev 势函数 V (ϕ) 随不同系统参数的变化规律 (a) α=0.4,b=0.8,σi=0.5,σd=0.02,δ=2;(b) M=1.3,b=0.8,σi=0.5,σd=0.02,δ=2;(c) M=1.3,α=0.4,σi=0.5,σd=0.02,δ=2;(d) M=1.3,α=0.4,b=0.8,σd=0.02,δ=2;(e) M=1.3,α=0.4,b=0.8,σi=0.5,δ=2;(f) M=1.3,α=0.4,b=0.8,σi=0.5,σd=0.02Fig.8.Variations of Sagdeev potential V (ϕ) with different parameters: (a) α=0.4,b=0.8,σi=0.5,σd=0.02,δ=2;(b) M=1.3,b=0.8,σi=0.5,σd=0.02,δ=2;(c) M=1.3,α=0.4,σi=0.5,σd=0.02,δ=2;(d) M=1.3,α=0.4,b=0.8,σd=0.02,δ=2;(e) M=1.3,α=0.4,b=0.8,σi=0.5,δ=2;(f) M=1.3,α=0.4,b=0.8,σi=0.5,σd=0.02.

图8 给出的数值模拟结果显示: 当马赫数M,nonthermal 电子数α,系统参数σi和δ依次增大时,压缩型孤立波的振幅ϕm将逐渐减小;而当trapped 离子数b和系统参数σd依次增大时,孤立波的振幅ϕm将逐渐增大,该结论与图2—图7 中二维自治系统的相图分析结果保持一致.因此可以得出结论: 马赫数、nonthermal 电子数和trapped离子数以及尘埃颗粒的未扰动数密度、温度及荷电量等系统参数对振幅大于零的压缩型孤立波的波形特征存在重要影响.

为了直观地了解孤立波的振幅和宽度等波形特征,可以利用椭圆方程的一般理论对Sagdeev 势方程(11)进行解析求解,得到该系统中非线性尘埃声孤波的形式如下[44]:

其中孤立波的振幅ϕm=-3A2/(2A3) ;孤立波的宽度D=.

图9 给出了同时含有nonthermal 电子和trapped 离子的复杂等离子体系统中非线性尘埃声波具体波形的变化规律.不难发现: 在给定的参数取值下,该复杂等离子体系统仅存在振幅大于零的压缩型孤立波,且当系统参数M,α,σi以及δ逐渐增加时,孤立波的振幅逐渐减小而宽度增大;而当系统参数b以及σd逐渐增加时,孤立波的振幅逐渐增大而宽度减小.这一结论与图8 中Sagdeev 势函数的分析结果保持一致.考虑到理论模型中各参数的具体表达式:σi=Ti/Te,δ=ne0/(Zdnd0),σd=Td/ZdTi.由此可知: 当电子的温度降低且其数密度增大,或者当尘埃颗粒的密度、荷电量以及温度下降时,孤立波的振幅将会变小;但是,如果离子的温度降低,那么孤立波的振幅则会增大.这说明: 在同时含有nonthermal 电子和trapped离子的多组分复杂等离子体中,诸如马赫数、nonthermal 电子和trapped 离子以及未扰动的尘埃颗粒数密度、温度及荷电量等系统参数对非线性尘埃声孤波的振幅、宽度等波形特征均具有重要影响.特别地: 当trapped 离子数和nonthermal 电子数增加时,孤立波的振幅和宽度会出现显著变化,这充分说明nonthermal 电子和trapped 离子的存在对复杂等离子体系统中非线性尘埃声孤波的传播波形存在不可忽视的重要影响.

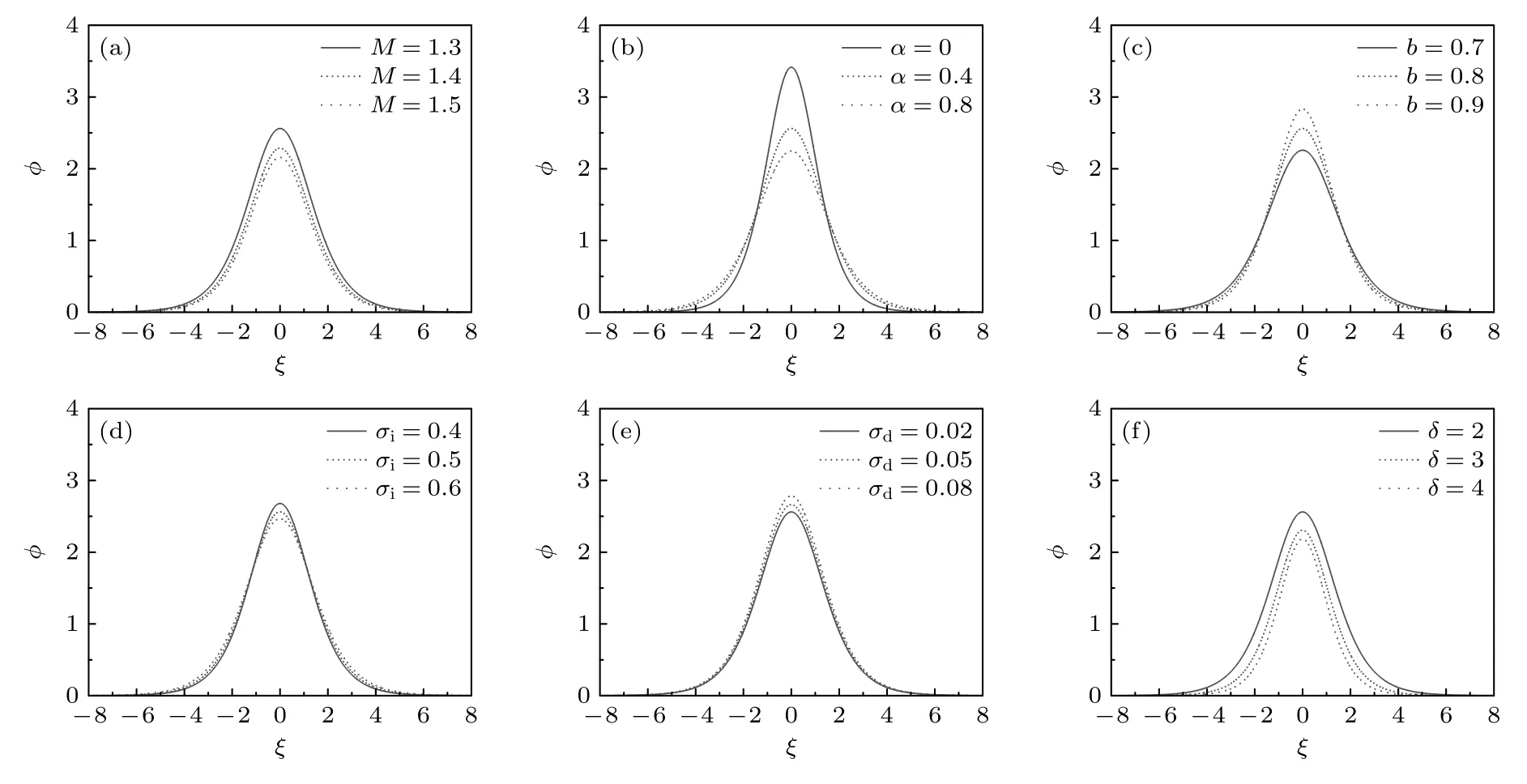
图9 孤立波 ϕ 的波形随不同参数的变化规律 (a) α=0.4,b=0.8,σi=0.5,σd=0.02,δ=2;(b) M=1.3,b=0.8,σi=0.5,σd=0.02,δ=2;(c) M=1.3,α=0.4,σi=0.5,σd=0.02,δ=2;(d) M=1.3,α=0.4,b=0.8,σd=0.02,δ=2;(e) M=1.3,α=0.4,b=0.8,σi=0.5,δ=2;(f) M=1.3,α=0.4,b=0.8,σi=0.5,σd=0.02Fig.9.Waveform variations of the solitary waves ϕ with different parameters: (a) α=0.4,b=0.8,σi=0.5,σd=0.02,δ=2;(b) M=1.3,b=0.8,σi=0.5,σd=0.02,δ=2;(c) M=1.3,α=0.4,σi=0.5,σd=0.02,δ=2;(d) M=1.3,α=0.4,b=0.8,σd=0.02,δ=2;(e) M=1.3,α=0.4,b=0.8,σi=0.5,δ=2;(f) M=1.3,α=0.4,b=0.8,σi=0.5,σd=0.02.

5 结论

本文研究了多种系统参数对同时含有nonthermal 电子和trapped 离子的复杂等离子体系统中非线性尘埃孤波传播特征的重要影响.首先,采用线性化方法推导得到非线性尘埃声波的色散关系;然后,借助Sagdeev 势方法推导得到二维自治系统、Sagdeev 势方程和Sagdeev 势函数的具体表达式;接着,通过数值模拟的方法分析了二维自治系统的相图随多种系统参数的变化规律.结果表明: 同时含有nonthermal 电子和trapped 离子的复杂等离子体系统中存在线性周期波解轨道、非线性周期波解轨道和同宿轨道.接下来,分析了Sagdeev 势函数的变化规律并确定该复杂等离子体系统仅存在振幅大于零的压缩型孤立波.最后,详细讨论了多种系统参数对非线性尘埃声孤波的振幅、宽度及波形的显著影响.结果表明: 诸如马赫数、nonthermal 电子和trapped 离子以及未扰动时的尘埃颗粒数密度、温度和荷电量等各种参数对非线性尘埃声孤波的振幅、宽度和波形等传播特性均具有不可忽视的重要影响.该理论研究结果将有助于空间和实验室环境等离子体中非线性波动过程的进一步研究工作的深入开展.