基于遗传算法的宽带渐变电阻膜超材料吸波器设计*

王超 李绣峰 张生俊 王如志†

1) (北京工业大学材料科学与工程学院,新能源材料与技术研究所,新型功能材料教育部重点实验室,北京 100124)

2) (北京航天长征飞行器研究所,试验物理与计算数学国家重点实验室,北京 100076)

近年来,基于超材料的电磁吸波器件由于其宽带、易制备等优势而备受各国研究者的广泛关注.本文为实现宽带电磁低可探测,提出一种渐变电阻膜-介质复合结构的超材料吸波器.基于传输线理论和阻抗匹配原理,对强吸波条件进行了分析.在单元结构设计方面,采用遗传算法在多变量域内全局搜索最优解,快速地确定出能够兼顾低频与宽带吸波性能的超材料单元结构与电阻参数,并对器件吸波性能与吸波机理进行了深入的探讨.仿真结果表明,在垂直入射下,所设计的超材料吸波器对1.62—19.16 GHz (相对带宽168.8%) 之间的入射波吸收率均大于90%,有效地向L 和K 波段拓展了吸收带宽.虽然在部分频段测试和仿真结果之间存在一定偏差,但两种类型的曲线随频率的变化趋势基本一致,这充分证明了所设计的超材料吸波器在低频宽带吸波领域具有潜在应用价值.

1 引言

随着电子信息以及雷达探测技术的不断发展,空间电磁环境日益严峻,在空间信息对抗中采用有效的手段对我方目标进行保护始终是人们研究和关注的重点[1].常用的目标防护措施包括诱饵伪装、雷达吸波、有源和无源干扰等,它们在一些特定的电子对抗领域有着自身独特的优势[2].其中雷达吸波通过吸收入射的电磁能,将其转化为热能或其他形式的能量并损耗掉,一方面可以降低目标的回波信号强度,减小被探测的概率;另一方面它也可有效地屏蔽外界电磁污染,保障设备正常运行[3,4].传统的吸波材料如铁氧体、钛酸钡、金属微粉等,通常具有吸收频带窄,密度大等缺点[5],而超材料的出现为吸波隐身技术提供了一种新的设计思路[6-9].2008 年,美国波士顿大学Landy 等[10]提出了首个基于电磁谐振的超材料吸波器,该结构在谐振频点表现出的吸波特性接近完美,这激起了人们对超材料吸波的研究热潮.在最近的十几年里,各式各样的超材料吸波器不断被人们提出,它们通过加载集总电阻元件[11-13]、复合多种吸波机制等方法实现了宽带或可调吸波[14-18].然而,通过对文献的总结,由于超材料、超表面天然的亚波长属性,使得其在低频段的应用受到一定限制,而能够兼顾低频的小型化宽带超材料吸波器受到人们越来越多的关注[19,20].

本文提出了一种基于渐变电阻膜的多层复合式超材料吸波结构,其单元由一种方形电阻膜在含导体底面的分层介质基板上多层叠加而成,各层方形电阻膜的表面阻值不同,这样一来,可通过对各层结构尺寸参数以及电阻膜表面电阻的优化取值,实现宽带吸收.首先介绍了加载电阻膜的超材料吸波单元构型及其等效电路,并阐明设计的核心思想;随后,将超材料吸波单元反射特性的数值解析过程与Matlab 遗传算法模型相结合,设计能够兼顾低频与宽带吸波性能的最优结构与电阻参数,并从能量损耗的角度对不同的吸波状态进行了研究;在阵列的电磁特性研究中,对比了有限阵列和无限阵列的反射系数仿真结果,并对包含20 × 20 个吸波单元的阵列进行雷达截面(radar cross section,RCS)仿真.最后,通过实验测试了所设计的超材料器件在2—18 GHz 的吸波性能,结果表明,该工作可为低频宽带超材料吸波器设计提供良好参考.

2 基于电阻膜的超材料吸波单元及其等效电路

本文拟采用加载了5 层电阻膜的超材料吸波器实现宽带吸波,待优化的单元结构及其等效电路模型如图1(a)和图1(b)所示.其中超材料吸波单元由电阻膜、聚对苯二甲酸乙二醇酯(polyethylene terephthalate,PET,其相对介电常数εr=3.0,损耗角正切 tanσ=0.061)、聚甲基丙烯酰亚胺泡沫(polymethacrylimide,PMI,其相对介电常数εr=1.05,损耗角正切 tanσ=0.001) 和金属地板构成.其中,PMI 自上而下的厚度分别用h1,h2,···,h5表示,各层PET 膜厚度均为0.8 mm.5 层方形电阻膜的宽度分别为w1,w2,···,w5.单元周期尺寸为p,金属背板采用厚度为0.036 mm,电导率为5.8×107S/m 的铜膜.

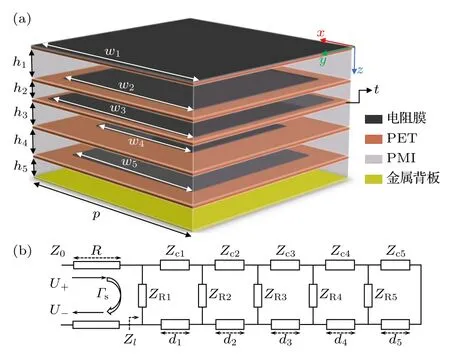
图1 基于电阻膜的超材料吸波单元结构及其等效电路模型Fig.1.Element configuration and its equivalent circuit model of the proposed resistive film-based metamaterial absorber.

图1(b)绘制了超材料吸波单元所对应的等效电路,其中Z0为自由空间的波阻抗,第一层至五层电阻膜可以等效为阻抗表面,分别用ZR1—ZR5表示.介质层和金属地板可分别等效为传输线和短路线,其中Zc1—Zc5表示每层介质的等效波阻抗,Zl表示吸波器件的整体负载阻抗 (或称输入阻抗).经多级串并联后,Zl=Rl+jXl,则单元反射系数可以表示为[21]

式中,Z0通常为377 Ω[22].根据(1)式可知,实现较强吸波的前提条件就是让负载阻抗的实部尽量与自由空间波阻抗匹配[23],虚部接近0,这样电磁波可自由通过吸波结构中的每一层,从而在电阻膜中损耗掉.本文基于电阻膜的超材料吸波设计的核心思想就是通过调节单元结构的尺寸参数以及各层电阻膜的阻抗实现满足预期的吸波效果.

3 超材料吸波器结构优化与吸波性能

3.1 遗传算法模型

在一些非周期的超材料设计中,研究者利用优化算法与阵列理论相结合,通过不断调节超材料阵列中单元相位排布来搜索最优解,并成功地实现了预期的散射效果[24,25].在这个过程中,由于时域求解器所剖分的超材料阵列网格数量庞大,在每一次迭代中都进行一次电磁仿真通常很难实现.因此,尽管通过优化得到的结果可以满足设计要求,但理论预测结果与实际仿真之间仍存在一定偏差,而这种现象却是无法完全避免的.

与上述方法不同的是,本文更关注超材料单元的反射幅度响应,而CST 软件中基于有限元法(finite element method,FEM)的频域求解器能够快速给出单元的S参数,Matlab 可以通过 ‘invoke’函数对CST 进行精确控制,实现参数的赋值、仿真和结果提取等操作.另外,Matlab 作为遗传算法的载体,可以通过多次迭代计算快速获得全局最优解[26].因此,可利用两种软件联合仿真的方法快速获得宽频带内最优吸波性能所对应的单元结构与电阻参数,本文基于遗传算法的单元优化设计流程如图2 所示.

图2 基于遗传算法的单元结构优化设计流程图Fig.2.Flowchart of the element’s configuration optimization design based on the genetic algorithm.

根据第2 节中对超材料吸波单元结构的分析可知,影响其反射幅度的可调参数主要是PMI 层厚度h、电阻膜的宽度w以及等效阻抗Z,而电阻膜的阻抗由电阻和电抗两部分构成,在设计过程中,主要对电阻R进行优化,这里忽略电抗部分主要是出于两方面考虑,首先,电阻膜的宽度间接反映了单元的电抗参数;其次,根据频域和时域求解器不同数值计算方法的仿真结果发现具有相同尺寸及电阻参数的单元模型在“unit cell”和“open”边界下仿真得到的S参数基本一致,如图3 所示,这说明相邻单元耦合形成的容抗 jω/C对反射幅度的影响并不明显.此处需要说明的是,CST 软件基于有限元法的频域求解器所提供的“unit cell”边界可自动模拟带有单元耦合的无限大周期结构,而基于有限积分法的时域求解器中“open”边界是将单个超材料单元的边界盒扩展到无穷大,其物理概念是该边界上无电磁波反射,从而模拟无限大的环境或微波暗室的边界.

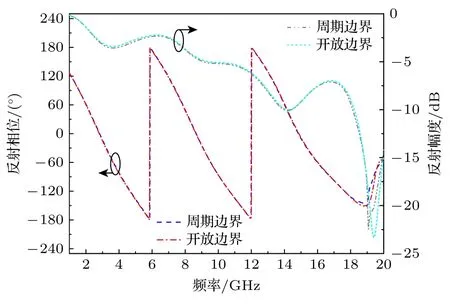
图3 相同尺寸及电阻参数的单元模型在“unit cell”和“open”边界下的反射响应Fig.3.Reflectance response of the metamaterial absorber with same dimension and resistance parameters under “unit cell” and “open” boundaries.

基于以上分析,对超材料吸波单元中15 个可变参数进行编码,并设定如下边界条件以约束整个优化过程:

其中PMI 膜厚度变化间隔为0.1 mm;电阻膜宽度变化间隔为0.5 mm;电阻膜阻值变化间隔选定为5 Ω.这样一来,单元所对应的所有可变参数经遗传算法中种群初始化后,可组合成一个90 bits 的二进制编码序列,其中5 层PMI 厚度参数共占30 位,5 层电阻膜宽度参数共占20 位,最后5 个电阻参数占40 位.优化过程中,将适值函数定义为超材料吸波单元在1—20 GHz 的频率范围内吸收率保持在0.9 以上,用数学方程表示为[27]

式中,Ab表示超材料单元的吸收率,它可以由 1-|S11|2计算得到[28].狄拉克δ函数的定义为

优化过程中,采用轮盘赌算子,单点交叉算子以及离散变异算子进行处理.在经历290 次迭代后,在电磁波垂直入射时,具有最优吸波性能的超材料单元参数见表1.

表1 具有最优吸波性能的超材料单元参数Table 1.Metamaterial element parameters with optimal wave absorption performance.

3.2 最优结构的吸波性能

利用CST 软件的频域求解器对所设计的超材料吸波单元进行正入射和斜入射的反射特性仿真,设置x和y方向的边界条件为“unit cell”,Zmin方向设置为“electric”,Zmax方向设置为“open add space”.Floquet 端口嵌入距离为10 mm.关于该超材料吸波体结构中的电阻膜,现实工艺中通常采用炭黑、水以及乳液按一定比例配成的乳状液体,利用喷涂技术制备而成,通过该工艺制备的电阻膜厚度从几微米到几十微米不等.为了简化计算,电阻膜的厚度可以忽略不计,将其等效为一表面电阻为R的二维平面结构,视电流密度在电阻膜中不同深度处分布均匀[19].图4(a)展示了所设计的超材料吸波单元在线极化波垂直入射时的反射系数与吸收率曲线.数据表明: 在垂直入射条件下,该吸波结构展现出良好的吸波效果.其反射系数低于-10 dB,吸波率超过90%的频率覆盖范围为1.62—19.16 GHz,相对带宽达到168.8%,完全覆盖了S,C,X 和Ku 波段,并有效地向L 和K 波段拓展.根据(1)式,定义结构输入阻抗与自由空间波阻抗的匹配系数为[29]

图4 垂直入射时超材料吸波单元的反射系数、吸收率(a)和归一化输入阻抗和阻抗匹配系数(b)随频率变化曲线Fig.4.Reflection coefficient,absorption (a),normalized input impedance and impedance matching coefficient (b) versus frequency curves of the designed metamaterial absorber element under normal incidence of linearly polarized waves.

接下来考察了所设计的吸波结构在不同极化的电磁波斜入射下的反射幅度对入射角度的依赖关系,图5(a)和图5(b)分别绘制transverse magnetic (TM)和transverse electric (TE) 极化下,入射角度从0° 增加至60° 时,单元反射系数随频率的变化曲线.从图5(a)和图5(b)可以看出,在TM 极化波入射下,入射角度从0° 增加至30° 时,反射系数在1.6—20 GHz 的频率范围内始终保持在-10 dB 以下,当入射角度增加至45° 时,虽然该频率范围轻微右移,但整体结构仍能在2.38—20 GHz 保持低反射,甚至在20 GHz 反射系数达到-37 dB.观察TE 极化下的仿真结果,可以看出,当入射角度从0° 增加至45° 时,结构反射系数在1.7—20 GHz 内均能够保持在-10 dB 以下,两种结果说明所设计的超材料吸波结构不仅具有良好的极化不敏感特性,同时对入射角度的依赖性不强.与反射系数相对应,图5(c)和图5(d)分别展示了单元在TM 和TE 极化的电磁波斜入射时的吸收率.可以看出,对于TM 极化来说,随着入射角度的增加,吸收强度基本都保持在0.9 以上,但带宽逐渐收缩.对于TE 极化来说,当入射角度增加到60° 时,在2.4—20 GHz 的频率范围,其吸收率仿真结果仍能保持在0.8 以上.对比60° 斜入射时TM 和TE 的吸收率曲线,可以看出两种极化下的仿真结果呈现出一定差异,其中在TM 极化下,单元表现出较高的吸收率,出现这种现象的原因可从两方面分析.首先,在斜入射时,不同极化模式下的自由空间波阻抗、吸波单元表面输入阻抗都有着各自的表示方式 (如=Z0cosθ,=Z0/cosθ),当θ=60° 时,自由空间波阻抗与结构表面输入阻抗在TM 极化下具有更好的匹配效果[31],从而使吸波单元在该模式下保持较低反射(图5(a)).其次,从物理层面分析,在斜入射的TM 极化下,磁场的方向始终平行于单元表面,从而有效驱动结构内部环形电流,实现良好的阻抗匹配[32].为了更好地研究极化和入射角度对超材料单元吸波性能的影响,图5(e)和图5(f)分别以极化角和入射角为纵坐标,以入射电磁波频率为横坐标展示了吸收率对入射电磁环境信息的依赖关系.从图5(e)可以看出,改变入射电磁波的极化角度对吸收率没有影响,这主要得益于单元结构的对称性.根据图5(f),三个强吸收区域主要分布在2—3 GHz,6—10 GHz以及13—18 GHz,且在1.5—20 GHz 的频率范围,吸收率均保持在80%以上.

图5 不同极化的电磁波斜入射下,超材料吸波单元的反射系数和吸收率随频率变化曲线 (a),(b) 反射系数;(c),(d) 吸收率;(e) 垂直入射时,吸收率对极化角的依赖关系;(f) 吸收率对入射角的依赖关系Fig.5.Reflection coefficient and absorption curves of the proposed metamaterial absorber under the oblique incidence of electromagnetic waves with different polarizations: (a),(b) Reflection coefficients;(c),(d) absorptivity;(e) dependence of absorptivity on polarization angle at normal incidence;(f) dependence of absorptivity on angle of incidence.

3.3 电磁损耗机理分析

从电磁损耗的角度出发,通过分析不同频率下单元结构内部的能量损耗情况,来对吸波机理进行更深入的研究.仿真结果表明,在所设计的电阻膜型超材料吸波器中,能量损耗主要分布在电阻膜以及靠近电阻膜的PET 介质上,图6(a)和图6(b)分别绘制了“unit cell”边界下TE 极化的电磁波垂直入射时,4 GHz (低吸收) 和7.6 GHz (高吸收)处五层电阻膜上能量损耗的分布图.从图6(a)和图6(b)可以看出,两种工作状态的相似之处是电阻膜对入射电磁波的吸收都是随着层数的增加而不断衰减,并且能量损耗主要集中在电阻膜的内部,其边缘损耗较弱;不同之处在于,低频时能量损耗主要分布在前三块电阻膜上,而高频时则是集中分布在前两块电阻膜上,这主要是由于电磁波在不同频率处的趋肤效应引起.另外,不难发现,高频时第一块电阻膜上的损耗明显高于低频时的情况.图6(c)和图6(d)分别展示了在4 和7.6 GHz的TE 极化波垂直入射时,超材料吸波单元中五块PET 膜上的能量损耗情况,可以看出,两种不同频率的电磁波激励下,能量在PET 膜的损耗主要集中在结构边缘 (单元与单元间的电磁耦合损耗),而且随着层数的增加,PET 介质上的损耗逐渐降低,这与电阻膜的损耗分布随传播距离的变化情况基本一致.

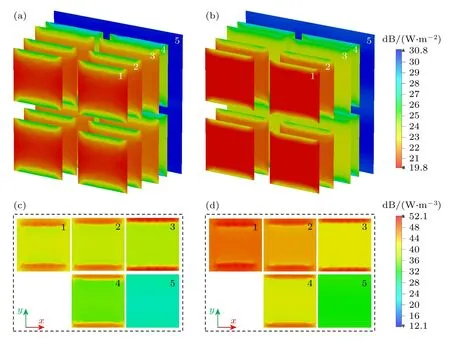
图6 电阻膜(a),(b)及PET 膜(c),(d)上的能量损耗分布图 (a),(c) 4 GHz,(b),(d) 7.6 GHzFig.6.Power loss distribution on the resistive film (a),(b) and the PET film (c),(d): (a),(c) 4 GHz,(b),(d) 7.6 GHz.

4 超材料阵列电磁仿真

4.1 反射特性

对具有20 × 20 个吸波单元的阵列进行建模,其三维模型如图7(a)所示,阵列整体尺寸为290 mm × 290 mm,厚度为21 mm.为了研究有限和无限周期阵列对器件吸收特性的影响,利用CST 时域求解器中的有限积分(finite integration technique,FIT)算法对所设计的超材料吸波器进行线极化波垂直入射时的S参数仿真,并对比吸波单元在“unit cell”边界下的反射系数.在仿真中,阵列x方向的边界条件设定为“electric”,y方向设定为“magnetic”,Zmin为“electric”,Zmax设定为“open add space”,波端口嵌入距离为四分之波长 (中心频率).由于阵列模型的对称性,为了简化计算,在“symmetry planes”中设置yz平面为“electric”,xz平面为 “magnetic”,这样一来,整体计算时间将减少至原来的1/4.在网格设置中,由于结构的规整性,使用六面体网格对整体阵列进行剖分,全局网格定义中,最大网格设定为最大仿真频率所对应波长的1/5,即3 mm,最小网格设定为最大网格尺寸的1/15,即0.2 mm,仿真结果如图7(b)所示.结果表明,所设计的吸波结构在有限的周期阵列下,其反射特性与基于“unit cell” 边界得到的结果基本一致,高频段1 dB 左右的偏差主要是由于有限阵列的边缘效应引起.另外,需要指出的是,虽然基于有限阵列的时域仿真能够更好地反映实际情况,但大阵列下所需的仿真耗时问题却不容忽略,相比于频域的FEM 算法 (耗时7 s),时域FIT 算法的仿真耗时高出将近70 倍 (8 m,6 s),因此本文关于阵列的吸收率分析均是基于单元的仿真结果而来.

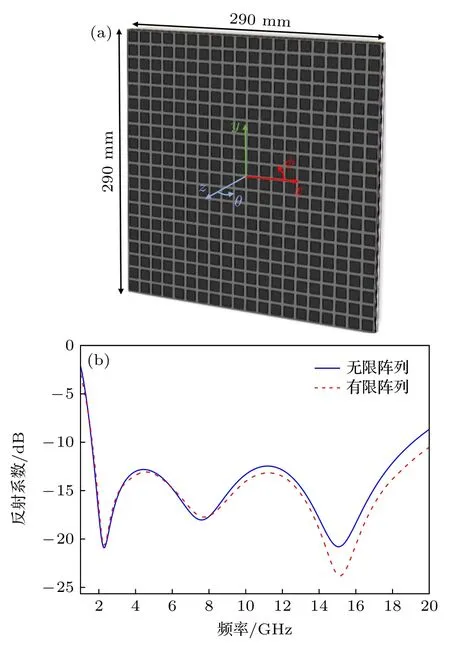
图7 (a) 超材料吸波阵列三维模型示意图;(b) 有限阵列与无限阵列的反射系数仿真结果Fig.7.(a) Schematic diagram of three-dimensional model of the proposed metamaterial absorbing array;(b) comparison of the simulated results of reflection coefficients for finite and infinite arrays.

图8 绘制了超材料吸波阵列在电磁波垂直入射下的表面输入阻抗随频率的变化曲线.可以看出,有限阵列构建的吸波器件表面输入阻抗与自由空间波阻抗之间匹配良好.

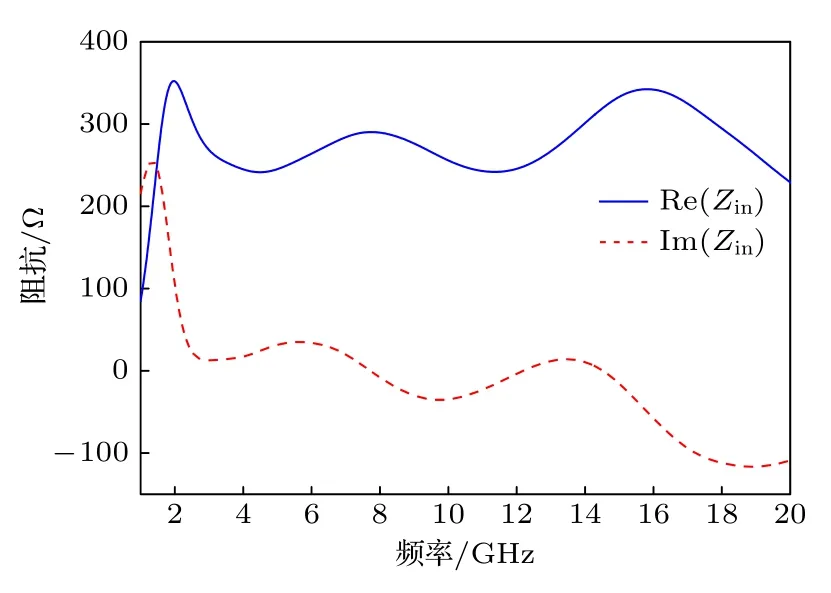
图8 超材料吸波阵列表面输入阻抗随频率的变化曲线Fig.8.Variation curves of surface input impedance of metamaterial absorber with frequency.

4.2 RCS 特性

对所设计的超材料吸波结构进行远场RCS 仿真,并对比同尺寸的金属平板,由于单元结构的四重对称性,在垂直入射时,对图9(a)中TM 极化下的仿真结果进行分析.从图9(a)可以看出,在1.7—20 GHz 的频率范围内,所设计的吸波结构均能实现10 dB 以上的RCS 缩减,三个RCS 缩减峰值分别出现在2.6,7.6 和15 GHz 附近,这与图4(a)中的强吸收频点完全对应.图9(b)和图9(c)展示了在不同极化的电磁波斜入射吸波结构时,镜像角度上的RCS 缩减值,在TM 极化下,随着入射角度的增加,吸波结构的10 dB RCS 缩减带宽逐渐收缩,但当角度增加到60° 时,所设计的超材料吸波器仍能在3.8—20 GHz 保持良好的吸波效果.在TE 极化下,当入射角度增加到30° 时,10 dB RCS 缩减带宽基本不变,但随着入射角度继续增加,达到60° 时,结构RCS 减缩性能明显下降.这主要是因为,在大角度入射的TE 模式下,电场与阵列中单元的耦合减弱,导致一部分能量在照射到结构表面后被直接反射掉.相比之下,斜入射时的TM 模式则不然,随着入射角度的增加,磁场方向始终是平行于吸波结构表面的,这样一来,较强的磁耦合仍能够使结构表面输入阻抗与自由空间波阻抗保持较好的匹配关系,从而实现良好的电磁吸收.

图9 (a) TM 极化波垂直入射时,超材料吸波阵列的RCS 仿真结果.(b),(c) 不同极化的电磁波斜入射时,吸波器的RCS 减缩性能仿真结果 (b) TM 极化;(c) TE 极化Fig.9.(a) Simulated RCS curves of the metamaterial absorber under the normal incidence of TM-polarized wave.(b),(c) RCS reduction performance of the proposed metamaterial absorber under oblique incidence of different polarizations: (b) TM polarization;(c) TE polarization.

5 超材料吸波器样件与实验验证

制备并测试所设计的超材料吸波器如图10(a)所示,加工的样件由20×20 个吸波单元构成,尺寸为290 mm × 290 mm,为了增加器件对可见光的吸收特性,首层PET 膜选为黑色.另外,对于PMI 介质夹层,使用泡沫电热切割机来精确控制各层的厚度尺寸.在测试环境中,一对工作在2—18 GHz 的喇叭天线通过同轴线与矢量网络分析仪(Rohde &Schwarz ZNB-20) 连接.在经过背景消除和定标体测量后,对超材料吸波器在5° 斜入射时的反射率进行测量,并通过计算获得了样件在该角度入射下TM 和TE 极化的吸收率曲线,结果如图10(b)所示.根据测试结果,超材料吸波器样件在2—18 GHz 的整个频率范围均能实现80%以上的电磁吸收.TM 和TE 极化的测试结果基本吻合,其中在9—12 GHz 的频率范围出现的偏差主要是由于器件的加工制造误差引起.对比测试与仿真结果,两种类型的曲线整体变化趋势基本一致,在6—13 GHz 出现的偏差可能与材料的选型有关,具体来说,在CST 仿真中,不同介质的电磁参数是通过算法拟合的方式得到的,这可能与测试中实际材料的电磁参数存在一定偏差.此外,对比不同极化的仿真结果,发现在小角度斜入射时,两种极化状态下的吸收率曲线完美重合.

图10 (a) 超材料吸波器样件及测试环境;(b) 所设计的超材料吸波器在不同极化的电磁波5° 斜入射时,吸收率测试和仿真结果Fig.10.(a) Photographs of the fabricated prototype and its measurement setup;(b) the measured and simulated results of absorption rate for the proposed metamaterial absorber under 5° oblique incidence of different polarizations.

对样件在不同极化的电磁波斜入射下的吸波特性进行测试,图11 分别绘制了所设计的超材料吸波器在30° 和60° 斜入射时,TM 和TE 极化下的吸收率曲线.结果表明,在60° 斜入射时,不同模式下的仿真和测试曲线基本重合,而在30° 斜入射时,TE 极化下的测试和仿真结果之间出现了一定的偏差,引起这种现象的原因主要由以下几点,一是前文所述的人为误差,如所选功能器件理论参数与实际参数不匹配、天线的未对准、板材翘曲等;另外,所选材料电磁参数的频率相关特性 (或称频率稳定性) 也是导致测试偏离仿真的重要因素.尽管如此,两种类型的曲线在2—18 GHz 的频率范围内整体变化趋势基本一致,测试与仿真结果之间的偏离程度明显小于文献[33]中所展示的结果,这充分验证了所设计的超材料吸波器的可靠性.

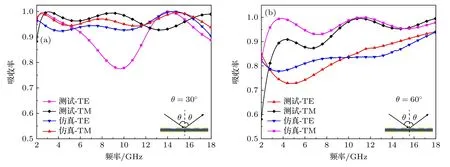
图11 不同入射角度的TM 和TE 极化电磁波斜入射时超材料吸波器的吸收率测试和仿真结果对比 (a) θ=30°;(b) θ=60°Fig.11.Comparison of measured and simulated results for the designed metamaterial absorber under oblique incidence of TM-and TE-polarized electromagnetic waves: (a) θ=30°;(b) θ=60°.

最后,为了评估所设计的超材料器件在电磁吸波方面的性能,将本文工作与其他宽带超材料吸波器在垂直入射时的吸波性能进行了对比[31,33-35],结果见表2 所列,其中λl表示90%吸波带宽最低频率所对应的波长,FBW 表示相对带宽.从表2 可以得知,尽管测试和仿真结果的匹配程度有待提升,但本文所设计的超材料器件在低频、宽带电磁吸波和相对厚度等方面都表现出良好的品质.

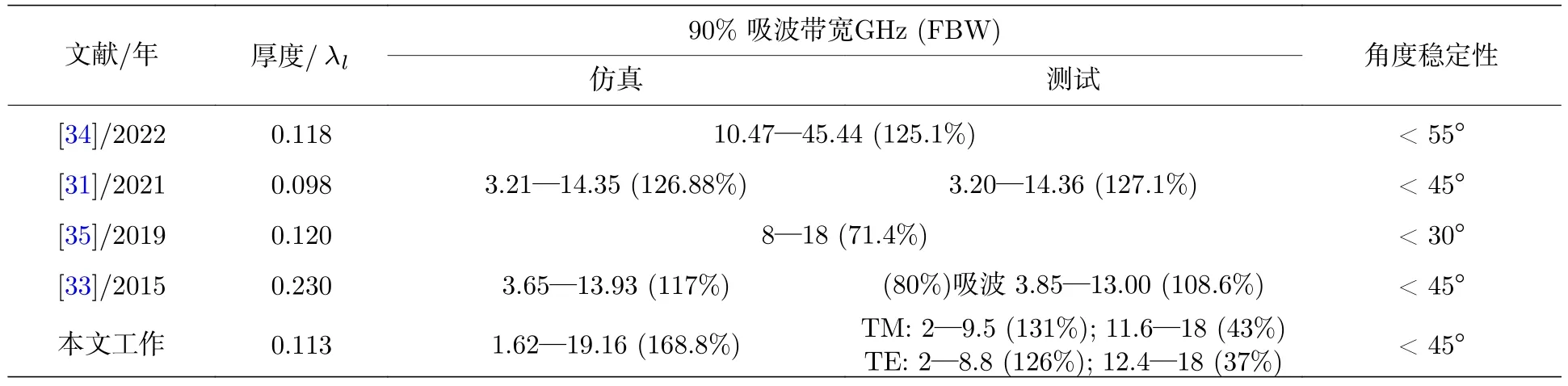
表2 本文工作与其他宽带超材料吸波器的性能对比结果Table 2.Comparison of the wave absorption performance between this study and other broadband metamaterial absorbers.

6 结论

本文为实现低频、宽带雷达吸波,提出一种具有5 层渐变电阻膜的超材料吸波器.在单元设计中,基于遗传算法对结构中3 个可调参数进行优化设计,使吸波性能有效地向L 和K 波段拓展.通过对电磁损耗分布的分析,明确了吸波单元工作在不同频率处的物理机制.单元及阵列的仿真结果表明,垂直入射下,在1.62—19.16 GHz 范围,入射波吸收率均大于90%,其相对带宽达到168.8%,轻微的频率偏移主要是由于有限阵列的边缘效应引起.在测试中,尽管人为的加工制造误差或材料频散特性使部分频段内测试和仿真结果之间呈现出一定偏差,但两种类型的曲线随频率的变化趋势基本一致,本文可为宽带超材料吸波器设计提供良好的仿真和实验参考.