如何用分类思想来认识图形
万李芳
数学中的分类思想,是根据数学对象本质属性的相同点与不同点,将其分成几个不同种类进行研究,从而解决问题的一种数学思想。它不仅有助于形成数学概念、还有助于构建数学知识体系。如何通过分类来认识图形?对此,教师可以展开如下教学过程。
一、初见分类,感悟标准
在已往的学习过程中,学生已经具备了一定的分类经验,通常可以将具有相同属性的物体进行归类。教师可借助学生的已有经验,组织学生进行第一次分类,让学生初步理解“分类标准”。
1.看一看,记一记
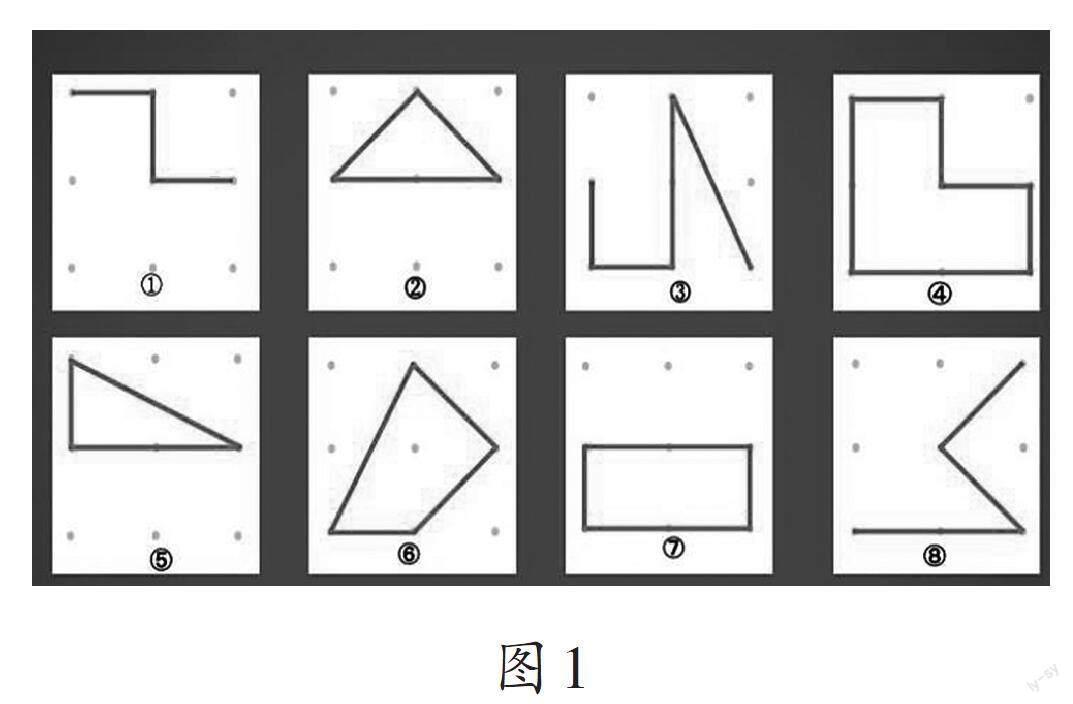
教师用课件呈现点子图和点子动图,让学生观察点在点子图上的运动,并记录其运动轨迹,形成8个不同的图形(如图1)。
2.选一选,分一分
教师组织学生将图1中的图形分为两类,引导学生将相同类别的图形归在一起,实则是让学生选取一个分类标准。学生根据图形是否首尾相连,将图形①、图形③、图形⑧分为一类,图形②、图形④、图形⑤、图形⑥、图形⑦分为一类。
3.反馈与小结
根据图形是否首尾相连,这些图形可分为开放图形与封闭图形。
二、选择标准,再次分类
1.看一看,选一选
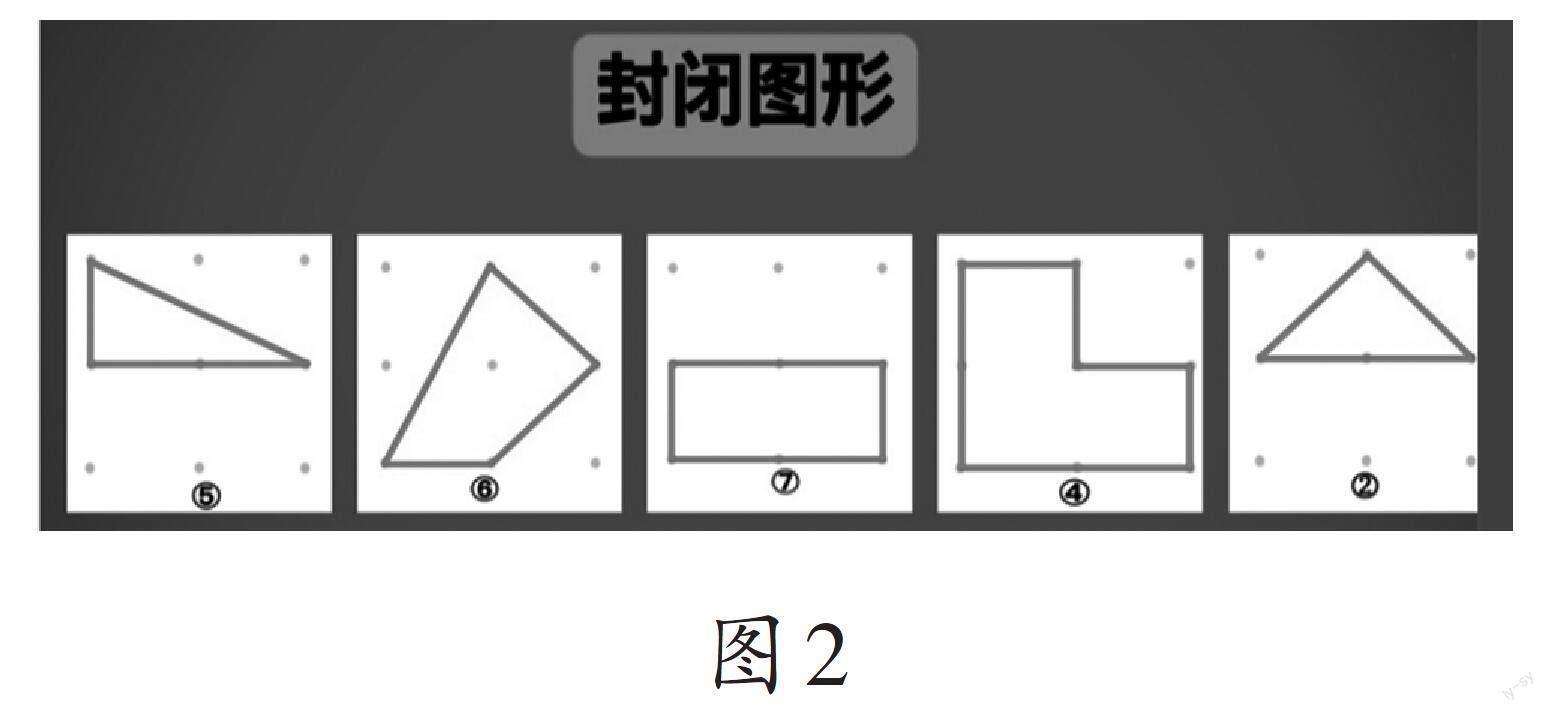
教师组织学生观察图2中的封闭图形,让学生再选择一个合适的分类标准进行分类。
在学生独立思考的基础上,教师组织全班反馈。学生根据不同的分类标准,对图形进行了如下分类。
(1)根据是否为三角形,将图形分为两类。
(2)根据边的数量,将图形分为三类。
(3)根据角的数量,将图形分为三类。
(4)根据顶点的数量,将图形分为三类。
2.想一想,认一认
教师组织讨论:在上述第(2)种、第(3)种和第(4)种分类中,为什么选择的分类标准不同,分类的结果却相同?
3.反馈与小结
在上述这些封闭图形(多边形)中,角、顶点、边的数量分别相等。
三、运用分类,理解图形
数学概念的形成往往源于分类活动,借助分類经验有助于学生认识图形。通过分类来理解图形的概念,可以提升学生思维的深度。
1.认一认,想一想
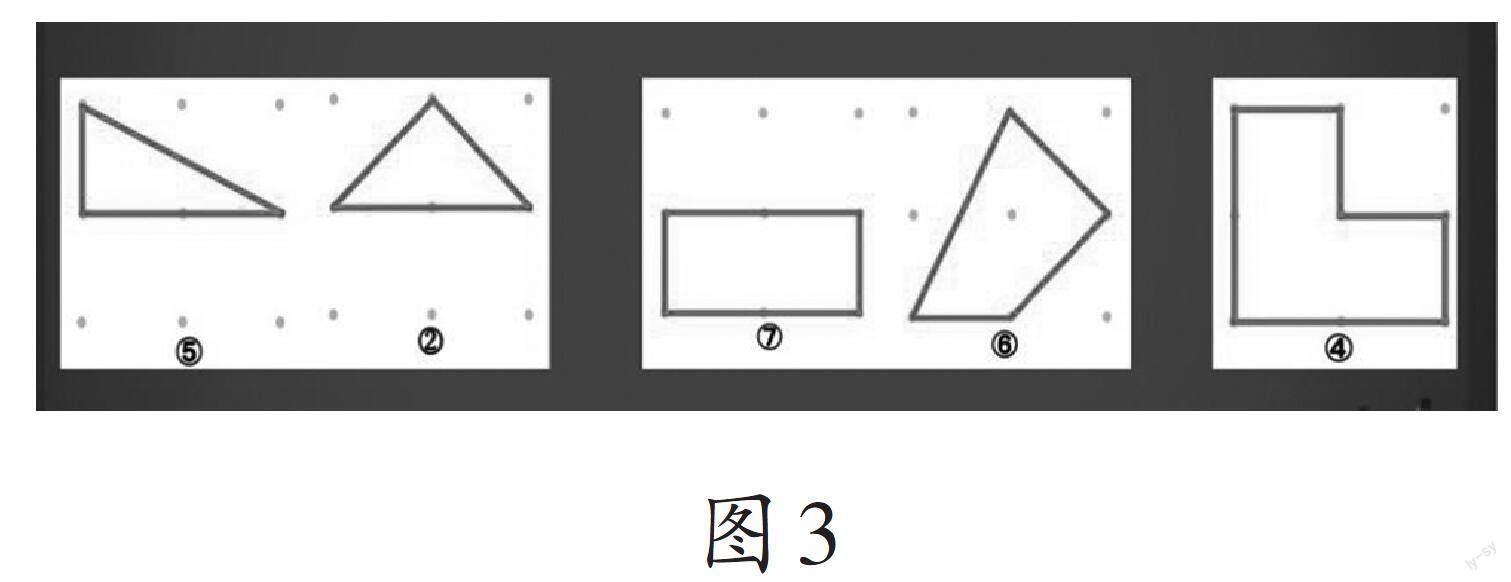
教师出示任务:请你们给图3中的前两类图形取名字,并说一说它们的特点。
2.反馈与小结
第一类图形可以称为三角形,也可称为三边形,它是由三条边围成的封闭图形。第二类图形可以称为四边形,是由四条边围成的封闭图形。
教师通过课件展示分类和概念的形成过程(如图4)。
在上述教学过程中,教师通过分类活动引导学生认识图形,发展分类思想,体会分类标准在概念形成过程中的重要作用。
(浙江省杭州市金都天长小学)

