不同单节理产状岩石力学性质数值模拟与强度预测模型

许 珂，刘学生,2，谭云亮,2，李学斌，高宇栋，宋 虎，唐颖钰

（1. 山东科技大学能源与矿业工程学院，山东 青岛 266590；2. 山东科技大学省部共建矿山岩层智能控制与绿色开采国家重点实验室培育基地，山东 青岛 266590）

0 引言

岩石作为一种复杂地质体，长期经历各种地质作用和人工活动，经受变形，遭受破坏，其内部往往存在各种复杂的节理、层理、断层等结构面，这些结构面的存在影响着岩石的稳定性和强度变形特性。节理岩石作为坝体、基坑、边坡、地下硐室等岩体工程中经常遇到的复杂介质，其力学性质直接影响工程的设计、施工及其长期稳定性[1]。

自20世纪以来，国内外众多学者围绕节理岩石力学特性[2-9]及强度预测方法[10-15]开展了大量研究，并取得了丰富的成果。在经典岩石力学领域，提出了几种著名的岩石强度理论并被广泛应用。如JEAGER发展了单弱面理论，认为含一组节理面各向异性岩石的破坏特征受节理面方位控制，基于该理论可对岩石抗压强度进行预测[16]。HOEK等[17-19]提出了著名的Hoek-Brown准则，通过选取合适的描述岩石软硬程度和破碎程度的经验参数预测节理岩石强度，对于节理面发育程度较高的岩石有较好的预测精度。后来，HOEK等[20]又基于GSI对Hoek-Brown准则进行修正，建立了广义Hoek-Brown屈服准则理论体系。随着损伤力学和断裂力学的发展，一些学者将其思想方法应用到节理岩石力学特性的分析中，如KAWAMOTO等[21]和SWOBODA等[22]采用节理面几何特征参数定义了二阶损伤张量，并引入节理面传压传剪系数等参数反映节理面间应力传递情况；孙卫军等[23]基于损伤力学原理和概率统计方法计算损伤张量，并将其引入节理岩石弹塑性损伤本构模型；朱维申等[24]基于Betti能量互易定理求出节理岩石的等效弹性张量，根据节理裂纹扩展过程中能量转换和相互作用建立了节理岩石的损伤演化方程；陈文玲等[25]从单节理尖端应力场引起的附加应变能入手，推导出能描述节理端部应力集中和相互影响的岩石细观损伤模型；任利等[26]基于断裂力学理论，求解了裂尖应力强度因子无量纲系数，进而改进了张破裂压剪准则，并基于此推导了单节理岩石抗压强度（该文中指初始断裂强度）预测公式；袁小清等[27-28]和赵怡晴等[29]考虑节理岩石宏观损伤和受荷细观损伤，基于断裂力学原理和Lemaitre应变等效假设推导了宏细观损伤耦合的非贯通节理岩石本构模型。

尽管目前已经建立了多种节理岩石损伤模型和强度预测公式，但这些模型和公式多存在以下两方面问题：一方面是公式中的部分参数难以准确测量和确定，譬如节理面的传压传剪系数等，经验参数选取不当会给预测结果带来较大误差；另一方面是模型本身关于由节理产状差异导致的不同破坏模式对岩石强度的影响考虑不充分，导致预测与试验结果有部分不一致，比如当节理倾角小于内摩擦角时，多认为岩石无法沿节理面滑移破坏，则岩石单轴强度应与无损岩石相同，这与试验结果不符。

针对以上问题，本文首先利用PFC建立不同单节理产状岩石数值模型，开展一系列单轴压缩数值模拟试验，研究节理尺寸和倾角对岩石力学特性的影响规律，在此基础上提出单节理岩石强度预测模型，并进行算例验证。研究可揭示并精确表征单节理产状对岩石破坏模式和单轴抗压强度的影响，便于工程现场实际应用。

1 单节理岩石单轴压缩数值模拟试验

1.1 室内试验

为了在数值模拟试验中获得与真实节理岩石一致的力学响应，首先进行室内试验获得真实红砂岩试样基本力学参数、应力应变全过程曲线及破坏形态，以作为数值模拟模型构建时的参照。室内试验岩石试件取样自红砂岩，岩样质地均匀，无明显裂隙，按照《煤和岩石物理力学性质测定方法第7部分：单轴抗压强度测定及软化系数计算方法》（GB/T 23561.7—2009）中试件规格加工成Φ50 mm×100 mm的标准圆柱体试件，共加工3个，并采用RLJW-2000型电液伺服试验机进行单轴压缩试验，加载速率为0.05 mm/min，获得试件的应力应变曲线和破坏形态，如图1所示。试件沿一定角度剪切破坏，平均单轴抗压强度为53.58 MPa，平均弹性模量为6.57 GPa，平均泊松比为0.327。

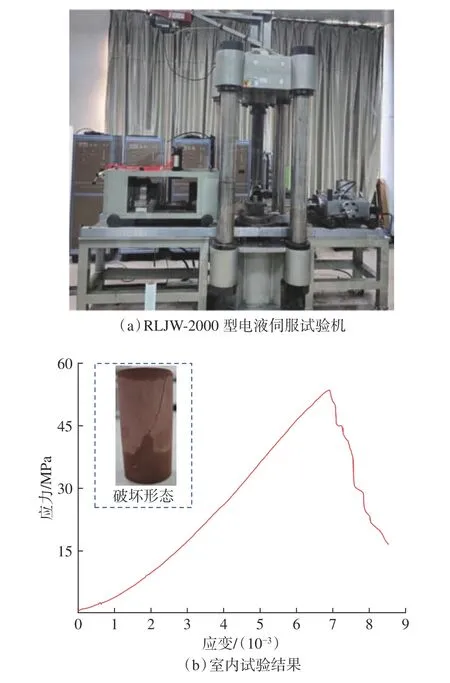
图1 室内试验设备与结果Fig. 1 Laboratory test equipment and results

1.2 建模与模拟方案

为更好研究岩石材料微观裂隙扩展及内部应力应变演化，选用PFC5.0颗粒流分析软件，利用合成岩体（SRM）方法[30]建立节理岩石数值模型。节理岩石由岩石基质及节理组成，其中，岩石基质采用BPM（Bonded Particle Model）表征，以PFC中颗粒单元为基础，颗粒间接触模型选用线性平行黏结（Linear Parallel Bond Model）模型模拟岩石颗粒间的相互作用。节理则采用PFC中DFN（Discrete Fracture Network）模型表征，DFN的接触模型选用光滑节理（Smooth-Joint）模型模拟节理面的滑移和张开。SRM方法将两者结合，形成准确模拟节理岩石力学性质的数值计算模型。

参考室内试验结果建立岩石基质数值模型，模型尺寸与室内试验岩石试件一致，高度为100 mm，直径为50 mm，在二维平面中呈现为长方形。颗粒与接触模型的细观参数，根据室内试验结果，采用“试错法”确定，即通过不断调整细观参数，直到岩石试件数值模型的单轴压缩模拟结果与相同条件下室内试验的弹性模量、泊松比和抗压强度等宏观性质尽量相近。经过多次匹配调整，最终确定了一组能够较好反映实际岩石宏观力学特性的数值模型细观参数，具体取值见表1，数值模拟与室内试验结果对比如图2所示。由图2可知，数值模拟得到的弹性模量、峰值强度和破坏形态与室内试验基本一致。尽管室内试验岩石试件选取均质无明显裂隙岩样制备，但仍无法完全杜绝试样内部细微裂隙存在，数值模拟和室内试验的应力-应变曲线在峰后存在少量差异；

表1 数值模型细观参数Table 1 Mesoscopic parameters of numerical model

图2 数值模拟与室内试验结果对比Fig. 2 Comparison of numerical simulation and laboratory test results

并且由于PFC中应力-应变曲线不能体现材料的初始压密阶段，数值模拟获得的峰值应变一般要小于室内试验获得的峰值应变[31]，根据文献[31]，模拟中这种程度的误差是可以接受的。综上，该数值模型及参数能较好地反映实际岩石的力学性质。

在PFC生成岩石基质模型后，基于PFC内置的DFN模型，在岩石上分别生成不同尺寸和倾角的单节理，得到包含不同单节理产状的岩石数值模型。根据前人文献中大部分实验结果，单节理岩石分别在节理尺寸最大和节理倾角在45°左右时受节理影响最大，强度也最低，因此，为保证模拟中节理对岩石力学特性产生足够影响，模型设置方案共2组18个模型，其中，第一组模型节理倾角均为45°，节理尺寸为5～50 mm，同时加入无损岩石作为对照；第二组模型节理尺寸均为40 mm，节理倾角为0°～90°，同样加入无损岩石作为对照。如图3和图4所示，图中浅色部分为岩石基质，深色部分为节理，上下黑色线条为加载板。

图4 不同节理倾角岩石数值模型Fig. 4 Numerical model of rock with different joint dip angles

采用恒定位移加载速率0.05 m/s[32-33]分别对模型进行单轴加载试验，当试件破坏且试件应力下降至峰值强度的30%时停止加载。

1.3 节理尺寸对岩石力学特性影响

对第一组模型进行单轴加载试验，得到试件的应力-应变曲线、单轴抗压强度和破坏形态特征，如图5和图6所示。

图5 不同节理尺寸岩石应力-应变曲线Fig. 5 Stress-strain curves of rock with different joint sizes

图6 不同节理尺寸岩石强度和破坏形态Fig. 6 Strength and failure modes of rock with different joint sizes

由图5可知，随着节理尺寸的增大，应力-应变曲线的峰值和斜率逐渐减小，说明岩石的单轴抗压强度和弹性模量均逐渐减小，损伤逐渐严重；同时，曲线峰值附近开始出现一定的塑性变形，节理尺寸超过30 mm时，峰后出现一定宽度的“平台”，即岩石的塑性和延性特性增强，破坏逐渐由无损岩石的脆性破坏转化为延性破坏，“平台”可能是由于节理岩石最弱承载截面到达应力承载极限后的整体破坏弱化过程中调整重组承载截面所导致。节理尺寸较小时，应力-应变曲线与无损岩石比较接近，如节理尺寸为5 mm时，应力-应变曲线与无损岩石几乎完全贴合，抗压强度和弹性模量等参数几乎相同；而尺寸达到50 mm时，曲线的峰值和斜率大幅减小，峰值强度较无损岩石减少约71%。

由图6可知，节理尺寸对岩石单轴强度影响较大，两者呈负相关关系。且在单轴压缩条件下，无损岩石的破坏模式呈现为沿一定角度穿切岩石的剪切破坏，节理岩石的破坏模式主要呈现为节理端部翼裂纹、次生裂纹的扩展破坏和穿切节理面的剪切破坏。在加载过程中，首先在岩石轴向两端和节理端部产生微裂纹，当节理尺寸较小（5～20 mm）时，由于岩石轴向两端微裂纹的产生、聚集速度更快，沿岩石基质弱面逐渐发育为贯通岩石的剪切裂纹；当节理尺寸较大（30～50 mm）时，由于节理端部微裂纹的产生、聚集速度更快，与节理面呈一定角度向轴向扩展，逐渐形成翼型裂纹和次生裂纹，最终造成岩石的贯通破坏。以上结果说明随着节理尺寸增大，节理损伤对岩石力学特性的影响逐渐增大，破坏模式逐渐从无损岩石的剪切破坏变为节理端部翼裂纹、次生裂纹扩展破坏。

1.4 节理倾角对岩石力学特性影响

对第二组模型进行单轴加载试验，得到试件的应力-应变曲线、单轴抗压强度和破坏形态特征，如图7和图8所示。

图7 不同节理尺寸岩石强度和破坏形态Fig. 7 Stress-strain curves of rock with different joint dip angles

图8 不同节理倾角岩石强度和破坏形态Fig. 8 Strength and failure modes of rock with different joint dip angles

由图7可知，当节理倾角较小时（0°～30°），随着节理倾角的增大，应力-应变曲线的峰值和斜率逐渐减小，说明岩石的单轴抗压强度和弹性模量均逐渐减小；峰值附近出现一定塑性变形，轴向应变增大，峰值后应力跌落速度变缓，说明岩石的塑性和延性增强。特别是在节理倾角为0°、15°时，曲线变为波浪形的多峰值曲线，说明节理的闭合、张开、滑移等行为对曲线产生较大影响，“多峰”现象即是节理岩石在外部载荷作用下内部这些重组行为在应力-应变曲线上的体现；其应力-应变曲线与无损岩石曲线相比具有显著形态差异，体现了其破坏模式应当与无损岩石存在一定差别。当节理倾角较大时（45°～90°），随着节理倾角的增大，应力-应变曲线峰值和斜率逐渐增大，说明岩石的单轴抗压强度和弹性模量均逐渐增大；峰值附近塑性变形减少，轴向应变减小，峰值后应力跌落速度加快，说明岩石的弹性和脆性增强；应力-应变曲线形态变化趋势又逐渐贴合无损岩石的曲线，说明其破坏模式又逐渐接近无损岩石。

由图8可知，岩石单轴抗压强度总体上随着节理倾角增大先减小后增大，呈现一种不对称的“U型”规律，且节理倾角0°的岩石强度要明显小于节理倾角90°的岩石强度。节理倾角75°、90°岩石的破坏以沿一定角度穿切岩石的剪切破坏为主，破坏模式和破坏面角度均十分接近无损岩石。节理倾角45°、60°岩石的破坏以节理端部次生裂纹扩展破坏为主，节理端部的应力集中效应使其更易产生和聚集微裂纹，微裂纹沿一定角度逐渐扩展发育形成次生裂纹，最终导致岩石贯通破坏，且次生裂纹角度与无损岩石破坏面角度较为接近。节理倾角0°～30°岩石的破坏以节理端部翼裂纹扩展破坏为主，同样因节理端部应力集中更易产生和聚集微裂纹，微裂纹与节理呈一定角度逐渐向轴向扩展发育形成翼裂纹，最终导致岩石贯通破坏。

以上得到的单节理岩石强度变化规律与Jeager单弱面理论当节理角度为45°+φ/2（φ为内摩擦角），单轴抗压强度最小的观点不一致，这是因为Jeager单弱面理论计算的是岩石沿单节理面滑动破坏的强度情况，往往出现于单节理为贯通节理的情况。但数值模拟发现单轴压缩时岩石并非都能沿单节理面滑动破坏，尤其对于非贯通单节理岩石，还存在穿切节理面破坏和节理端部翼裂纹扩展引起的破坏的情况，本文将依据模拟所发现规律在下节具体分析节理岩石不同破坏模式对其单轴抗压强度的影响机理。

2 单节理岩石单轴抗压强度预测模型

2.1 模型构建

由1.2节数值模拟发现，单轴压缩条件下，节理岩石在节理倾角不同时具有不同破坏模式，使用单一的强度理论难以准确分析不同破坏模式下节理产状对岩石单轴抗压强度的影响。因此，根据模拟结果分类讨论，分别采用适合岩石相应破坏模式的岩石力学理论对岩石的单轴抗压强度进行分析。

对单轴压缩状态下的单节理岩石进行受力分析，如图9所示。图9中2a为节理尺寸；β为节理倾角（节理面与水平方向的夹角）；σj、τj分别为节理面上的正应力和切应力；A1、A2分别为完整岩石垂直轴向力和平行轴向力的截面积（二维情况下即为岩石的宽度和高度）。

图9 单轴压力下的单节理岩石Fig. 9 Single jointed rock under uniaxial pressure

无损岩石在单轴压缩状态下沿一定角度发生剪切破坏。根据Mohr-Coulomb准则，可以计算出无损岩石剪切破坏时破坏面倾角θ0=45°+φ/2。

1.2 节中无损岩石数值模型的内摩擦角φ=42°，计算得到破坏面倾角θ0=66°，与模拟结果（图6和图8）基本一致。

模拟得到单节理岩石在单轴压缩状态下，主要分为以下三种破坏模式：①穿切节理面贯通岩石的剪切破坏，破坏面倾角接近无损岩石破坏面倾角θ0；②节理端部次生裂纹扩展导致的岩石剪切破坏，次生裂纹倾角同样接近θ0；③节理端部受压起裂形成翼裂纹，沿一定角度扩展导致的岩石破坏。前两种破坏主要发生在节理倾角φj≤β≤90°的情况，第三种破坏主要发生在节理倾角0°≤β＜φj的情况（φj为节理面的内摩擦角，第1节数值模拟中φj=35°）。

两种情况的区别在于，受压时节理面上是否存在使节理面两侧产生相对滑动倾向的切向应力。单轴压缩时加载应力为σ，倾角为β的节理面上正应力σj和切应力τj，见式（1）。

因节理面上黏聚力远小于摩擦力[34]，可近似忽略不计，则节理面上的切向滑动力，见式（2）。

针对这两种情况分别进行理论分析。

1）节理倾角φj≤β≤90°时。该条件下岩石受压时节理面处存在切向滑动力，节理面两侧岩石存在相对滑动倾向，破坏模式以沿弱面穿切岩石或次生裂纹扩展的剪切破坏为主，且破坏面倾角与无损岩石类似。仅由于受到节理影响，岩石强度有所下降，因此基于损伤力学对其进行分析。

根据损伤力学思想，应提出合适的损伤变量以反映节理对岩石力学特性的影响。传统损伤力学的一类观点是按照损伤面积定义损伤变量，假定有效承载面积的减少是造成材料损伤的主要因素，根据Kachanov-Rabotnov经典损伤理论[35]，对于损伤状态岩石，可等效为有效承载面积减小的无损状态岩石，如图10所示。

图10 单轴受力状态的损伤Fig. 10 Damage of uniaxial stress state

图10（a）是岩石的原始损伤状态，面积微元A上所受力矢量为P，应力为σ=P/A，Ω为损伤变量，用于描述岩石的损伤程度；图10（b）将岩石视为有效承载面积减小为A*的等效无损状态，相应的岩石所承受有效应力σ*要大于原始应力σ。

基于以上分析，按材料损伤面积定义损伤变量Ω的计算方式，使用节理产状参数进行计算，包括节理尺寸2a、节理倾角β，将单条节理对岩石附加的损伤变量定义为式（3）。

式中，A1、A2分别为完整岩石垂直轴向力和平行轴向力的截面积；Ω1、Ω2分别为岩石垂直轴向力方向与沿轴向力方向的损伤分量。

根据式（3），求得的损伤变量的两个分量Ω1、Ω2，实际上等于节理面投影在岩石两个方向截面上的面积损伤率。

假设节理岩石在等效无损状态下的剪切破坏服从Mohr-Coulomb准则，根据数值模拟结果，满足节理倾角φj≤β的岩石在单轴压缩时沿倾角为θ0=45°+φ/2的破坏面发生剪切破坏，则节理岩石的单轴抗压强度σjc见式（5）。

无损岩石在单轴压缩时同样沿倾角θ0剪切破坏，单轴抗压强度σc满足式（6）。

则由无损岩石单轴抗压强度σc和损伤变量Ω，可计算节理岩石单轴抗压强度σjc，见式（7）。

2）节理倾角φj≤β≤90°时。该条件下岩石受压时节理面处不存在切向滑动力，节理面两侧岩石无法相对滑动，岩石破坏模式主要是节理端部翼裂纹扩展造成的岩石破坏，因此，基于断裂力学进行分析。单轴压力下单节理岩石翼裂纹模型如图11所示。

图11 单轴压力下单节理岩石翼裂纹模型Fig. 11 Wing crack model of single jointed rock under uniaxial pressure

无限大板中，节理尺寸为2a，节理倾角为β的节理端部在单轴压缩应力σ下I型应力强度因子和II型应力强度因子见式（8）。

实际情况下岩石存在尺寸，根据ISIDA等的研究[36]，在考虑节理尺寸和岩石宽度的条件下可将应力强度因子修正为式（9）。

根据周群力[37]提出的压剪断裂判据，对于压力作用下剪切荷载引起的裂纹扩展与断裂，其应力强度因子满足式（10）。

式中：λ为压剪系数，由材料本身性质决定；KIIc为压缩状态下的剪切断裂韧度，也由材料本身性质决定。两参数均可取样后由室内单边裂缝试件压剪断裂试验[38]测定。

将式（9）代入式（10）得单节理岩石起裂强度σjci，见式（11）。

参照任利[26]方法定义反映单轴压缩状态下起裂强度大小的无量纲抗断裂能力R，见式（12）。

式中：R取值范围为（0，1），R=0表示原节理面一经加载就失稳扩展，起裂强度取值为0；R=1表示原节理面不会断裂破坏，起裂强度可按无损岩石取值。

根据文献[39]～文献[41]，岩石的起裂强度与单轴抗压强度呈正比例关系（为0.4～0.5倍），则认为两者变化趋势一致，加入比例系数k（k为岩石的单轴抗压强度与起裂强度的比值，仅与材料本身性质决定）修改R为Rj，以反映由于翼裂纹扩展导致断裂破坏岩石的单轴抗压强度的变化趋势，此时单节理岩石的抗压强度σjc可由式（13）近似计算。

式中：σc为无损岩石的单轴抗压强度；k为比例系数。

总结以上两种情况，得到单节理岩石单轴抗压强度预测公式，见式（14）。

式（14）根据节理倾角与节理面内摩擦角的关系分为两部分，分别对应于非贯通单节理岩石的不同破坏情况，φj≤β≤90°时对应岩石沿弱面剪切破坏的情况，0°≤β＜φj时对应岩石因节理端部翼裂纹扩展破坏的情况，充分考虑了单节理岩石在单轴压缩时由于不同几何特征节理所导致的不同破坏模式对岩石强度的影响（对于贯通节理岩石沿节理面滑动剪切破坏的情况，则可继续沿用单弱面准则）。式（14）主要适用节理宽度（开度）相对节理尺寸较小的节理，节理受压闭合，故节理宽度可忽略不计；对于节理宽度（开度）较大，节理受压难以闭合的张开型节理，则节理面两侧岩石无法接触，节理面上不存在摩擦力，此时对于任意节理倾角，两侧岩石受压均会产生侧向滑动，模型符合情况1）等效为有效承载面积减小的无损岩石，无论节理倾角如何强度可由式（14）中第一部分即式（7）直接计算。

此外，对于内含充填物的节理岩石，情况则较为复杂，充填物的存在会抑制拉应力的发展，导致充填节理岩石具有更大的裂纹起裂应力水平，单轴抗压强度预计会高于式（14）计算结果，高出程度与充填材料力学特性有关。因此，式（14）不适用，需要根据充填材料性质对无损岩石强度σc和节理内摩擦角φj进行修正，有待进一步研究。

参数节理尺寸2a、节理倾角β、节理内摩擦角φj、无损岩石强度σc、岩石垂直轴向力截面积A1均可由现场测量或基本力学实验测定，系数λ、k只与材料本身性质有关，既可由室内试验测定也可根据岩石岩性取值，便于在实际工程中推广应用。

2.2 算例验证

为验证2.1节提出的预测模型的准确性，对不同节理尺寸和节理倾角单节理岩石的单轴抗压强度进行预测，并与室内试验和数值模拟结果相比较。

室内试验试件与前文取样自同一批均质红砂岩，采用同样方法制备为Φ50 mm×100 mm的标准圆柱体试件，分别在试件上切割出不同节理倾角尺寸的单节理，共两组，第一组节理切割长度30 mm，深度贯通试件，节理倾角分别为0°、30°、45°、60°、90°，每种角度3个；第二组节理切割长度10 mm，深度贯通试件，节理倾角分别为0°、30°、45°、60°、90°，每种角度3个。加载设备和方式与1.1节室内试验相同，最终每种节理产状岩石的强度取3个数据的平均值。岩石试件如图12所示，室内试验得到单节理岩石破坏模式如图13所示，单轴抗压强度见表2（编号规则为：节理切割长度-节理倾角-编号）。

表2 单节理岩石室内试验的单轴抗压强度Table 2 Uniaxial compressive strength of single jointed rock in laboratory test

图12 红砂岩单节理岩石试件Fig. 12 Red sandstone single joint rock specimen

图13 室内试验单节理岩石破坏模式Fig. 13 Failure mode of single jointed rock in laboratory test

图13是单节理红砂岩岩石试件经单轴压缩后的破坏模式，岩石上部分裂纹和缺损是单轴压缩破坏时，部分岩石块体崩碎、跌落所造成的二次破坏。排除以上干扰因素后，可以观察到节理倾角较小时，节理端部翼裂纹扩展破坏特征较为明显；而节理倾角较大时，贯穿节理的剪切破坏更为明显。另外，还可以发现节理尺寸较小时，岩石压缩破坏时更容易崩碎，说明其脆性更强。这些现象都与上文理论分析一致。

数值模拟参照1.2节建模过程及力学参数，设置四组单节理岩石模型，各组节理尺寸2a分别为40 mm、30 mm、20 mm和10 mm，每组中设置节理倾角β范围为0°～90°，加载过程也与1.2节数值模拟相同。

数值模拟得到单节理岩石破坏模式如图14所示。破坏模式受节理产状影响规律同样与2.1节分析一致，随着节理倾角变大，节理岩石的主要破坏模式逐渐从翼裂纹扩展破坏转变为穿切节理的剪切破坏；且随着节理尺寸变大，节理端部的翼裂纹扩展破坏特征更加明显。

图14 数值模拟单节理岩石破坏模式Fig. 14 Failure mode of single jointed rock of numerical simulation

需要指出的是，由于试件的横向截面是圆形，室内试验的三维情况下节理切割长度（图15）与数值模拟的二维情况下节理尺寸是不同概念，对应节理在垂直轴向力方向的面积损伤率（即Ω1）不同，相应的计算出预测强度也有所不同。

图15 单节理岩石试件损伤Fig. 15 Damage of single jointed rock specimen

根据2.1节公式中系数λ、k只与材料本身性质有关，参考文献[38]～文献[41]得到参数大致取值范围，并拟合已做试验、模拟数据得到适合红砂岩的公式参数，取k= 2、λ=0.4，代入式（14），对不同节理产状的单节理岩石单轴抗压强度进行预测，并对比验证试验和模拟结果如图16和图17所示。

图16 单节理岩石的单轴抗压强度预测和试验平均对比Fig. 16 Uniaxial compressive strength prediction and experimental comparison of single jointed rock

图17 单节理岩石的单轴抗压强度预测和数值模拟对比Fig. 17 Uniaxial compressive strength prediction and simulation comparison of single jointed rock

由图17可知，预测模型的理论计算与试验和模拟结果变化趋势基本一致，贴合良好，误差较小，相关系数R均大于0.96，平均相对误差5.89%，这在实际工程中是可以接受的（假如后续针对不同岩性的岩石大量开展试验，采用试验数据拟合得到精度更高的λ、k经验参数，预测模型的精度还可以提升）。因此，上述单节理岩石单轴强度预测模型具备足够的精度。

3 结 论

1）节理尺寸主要对岩石的强度有较大影响。随节理尺寸增大，节理岩石的单轴抗压强度逐渐减小，两者呈负相关关系，节理尺寸由5 mm增大至50 mm时，单轴抗压强度减小71%。

2）节理倾角对岩石破坏模式和单轴抗压强度的影响与节理倾角β和节理面内摩擦角φj的相对大小有关。随节理倾角增大，岩石单轴抗压强度先减小后增大，呈不对称的“U型”规律，当0°≤β＜φj时破坏模式主要是节理端部翼裂纹扩展破坏；当φj≤β≤90°时则为沿一定角度穿切岩石或次生裂纹扩展的剪切破坏。

3）基于损伤力学和断裂力学思想，充分考虑由于节理产状不同所导致的不同破坏模式对岩石强度的影响，建立了单节理岩石单轴抗压强度预测模型和公式，相关参数物理意义明确且易于获取。算例验证表明，预测模型和公式精度较高，相关系数R大于0.96，平均相对误差仅为5.89%。