面向动态交通流多步预测的时空图模型

杨 平，李成鑫，刘宜成，吕淳朴

(1.四川大学 电气工程学院，四川 成都 610065；2.清华大学 自动化系，北京 100084)

0 引 言

准确的短时交通流预测对减少路网中交通拥堵具有重要的意义。近年来，一些基于图卷积网络(GCN)的高级深度学习模型得到了广泛的应用。Liu等[1]指出，以往基于CNN[2-4]的模型将路网视为一幅图像或网格的集合，仅适用于欧式空间；而基于GCN[5-8]的模型则将路网视为一种图结构(Graph)，其中节点和边分别代表传感器及传感器之间的相关性，通过对拓扑信息进行编码可以提取非欧几里得空间中的拓扑特征。如Zhao等[9]提出一种空间卷积模块，多层GCN依次向后传递来学习图结构矩阵，再与门控扩张卷积提取的时间特征进行融合来进行预测。

目前多数研究学习到的图结构可以充分反映节点间的显式相关性，但实际路网中的空间关系有时会随着时间特征而变化，即一些隐式空间特征未被提取导致空间依赖建模不充分。本文提出一种基于时空数据嵌入的动态图卷积预测模型(TSDE-dGCN)来建模节点间时空依赖关系。将时空数据作为整体来考虑，模型尝试将时空数据的图表示学习视为时间维度信息和二维空间维度信息的聚合，生成蕴含有时空信息的三维邻接张量以更好提取节点间隐式交互作用；此外，在图卷积网络中引入RNN组件沿着时间维度演化GCN参数更新，捕获图序列的动态性。在两个公开数据集(METR-LA和PEMS-BAY)上进行本文模型的实验验证，结果表明，所提模型具有较好的性能。

1 模型设计

1.1 TSDE-dGCN模型框架

本文预测模型整体框架如图1所示。模型由以下几部分组成：输入模块、时空数据嵌入模块、空间卷积模块、时间卷积模块、残差连接模块及输出模块。将一个时间卷积模块和一个空间卷积模块封装成一个时空块(ST-Block)，通过叠加多个时空块的形式可以有效处理不同时间水平上的时空依赖性。如分布在低层的块可处理短期时间信息，分布在顶层的时空块可处理长期时间信息。

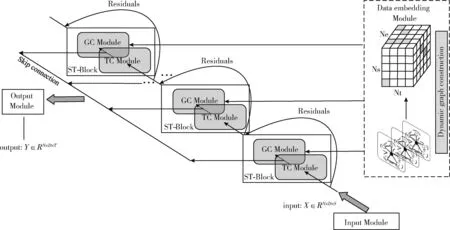
图1 预测模型整体框架

1.2 时空数据嵌入模块

1.2.1 图表示学习

Embedding在数学上表示一种空间映射，包含两个阶段：编码和解码。如Node Embedding的目的就是将节点映射到Embedding空间中，它可以自动编码原网络信息，映射后节点的相似性就反映了原网络中节点之间的相似关系，映射过程如图2所示，图中ENC(u) 表示对节点u进行编码得到zu。 与编码阶段相对应的是解码阶段，即将Embedding空间中的向量映射成相似性分数，定义一个节点相似性函数来评估节点在原网络中的相似性，如式(1)所示，表示原始网络中节点的相似性约为节点嵌入的相似性。相似性函数为学习节点嵌入特征提供了优化条件

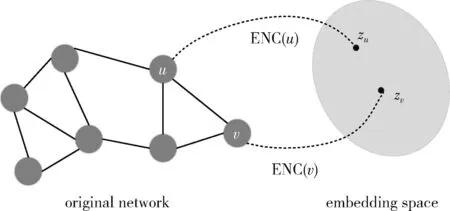
图2 节点嵌入过程

(1)

1.2.2 深度游走算法

深度游走算法(deepwalk)主要用来学习节点嵌入向量，主要分为3个过程：

(1)随机游走(random walk)：给定一个Graph和一个起始点，随机选择该点的某个邻居节点并移动到该邻居节点；根据当前节点随机选择一个邻居节点，移动到该邻居节点，重复上述步骤……通过这种随机游走访问Graph节点的方式可以产生随机序列。以图3为例，其产生的随机序列为：start_node->4->5->8->9->8->10。通常从每个节点执行32至64次随机遍历就足够表示节点间结构关系。

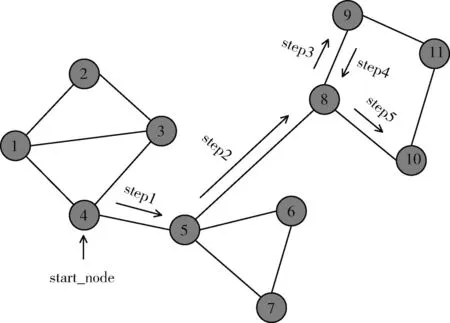
图3 随机游走过程

(2)训练skip-gram：将随机游走采样得到的序列作为输入，进一步通过最大化预测相邻节点的概率来预测周围节点，对这一过程进行不断训练和学习。

对于给定节点序列 {w1，w2，…，wT}， Skip-gram模型的训练目标是使式(2)平均对数概率最大化

(2)

其中，c是选择周围节点的窗口大小。

假设对于某个中心节点wI， 它的某个相邻节点为wo， 使用最大软函数定义p(wO|wI) 如式(3)所示

(3)

其中，W表示包含所有节点在内的二维图表，uw∈Rd和vw∈Rd表示节点w的d维输出、输入嵌入向量表示，所有节点的输入输出向量都是要学习的参数，即U={uw|w∈W}，V={vw|w∈W}， Skip-gram模型是三层神经网络，其中U和V分别表示神经网络的两个连接边参数矩阵。

整体预测流程简化如图4所示。

图4 Deepwalk算法

1.2.3 动态邻接张量

动态时空依赖性如图5所示。节点之间的线表示节点之间的依赖关系，线条粗细表示节点之间的影响权重不同。将节点e作为观测节点，可以观察到同一时刻不同位置的节点对节点e的影响权重是不同的，而相同位置的节点对节点e的影响在不同时刻也发生变化。因此，图的结构特征以及节点特征会依据时间动态变化，故构建邻接矩阵时要充分考虑节点之间的属性特征。

图5 动态时空依赖

本文将节点嵌入扩展到三维空间中，如图6所示。通过随机游走的方式采样各个节点作为中心节点，构建中心节点嵌入矩阵Es∈RNs×d， 之后利用Skip-gram模型训练学习各个源节点的周围邻居节点，构建邻居节点嵌入矩阵Ee∈RNe×d， 再结合具有日趋势性和周周期性的时隙嵌入矩阵Et∈RNt×d， 再分配一个核心张量Ek∈Rd×d×d以统一嵌入维度，其中，Nt，Ns，Ne，d分别代表时隙数量、中心节点的数量、目标邻居节点的数量和嵌入维度，o、q、r分别代表嵌入过程中的维度。通过将节点嵌入到Embedding空间中随训练一起学习更新，可以自动学习节点之间的相似性。在一定的嵌入维度下，模型可以学习到每个节点的向量表示，包含了该节点及其邻居节点的当前和历史时刻信息的聚合。邻接张量的计算方法如式(4)所示

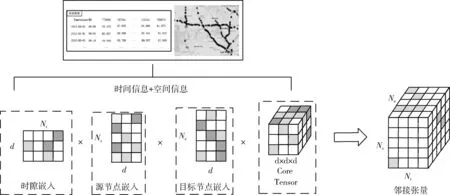
图6 动态邻接张量嵌入过程

(4)

1.3 空间卷积模块

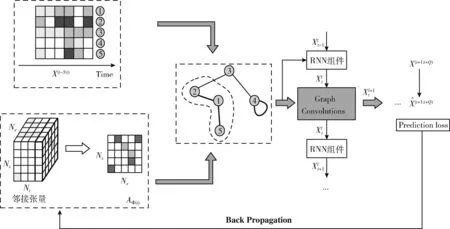
图7 动态图卷积

(5)

(6)

(7)

(8)

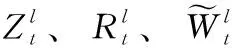
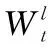
本文的动态图卷积定义如式(9)所示

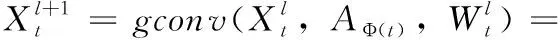
(9)

1.4 时间卷积模块

时间卷积模块中主要是利用时间卷积网络(TCN)提取交通数据的多层次时空特征，加强特征间的时间依赖性。时间卷积网络主要由扩张因果卷积(dilated causal convolution)网络组成。在因果卷积(causal convolution)的基础上添加可以控制跳跃距离的扩散步长(dilation)，使卷积网络的感受域可以随着层深度的增加呈指数扩张。这样的结构使时间卷积网络能够在更少层中捕获更长序列。此外门控机制可以控制网络层之间的信息流传输。

1.5 输出模块

多数深度模型都会添加残差模块以解决网络过深导致的梯度消失和梯度爆炸问题，网络结构参见文献[10]。

在训练过程中，目标是尽量减小模型预测值与真实交通观测值之间的误差。损失函数如式(10)所示

(10)

2 实验与结果

2.1 实验数据

为了验证本文模型的性能，在两个公开的大规模交通数据集上(METR-LA与PEMS-BAY)[10]进行了实验。表1列出了两个数据集的详细统计信息。

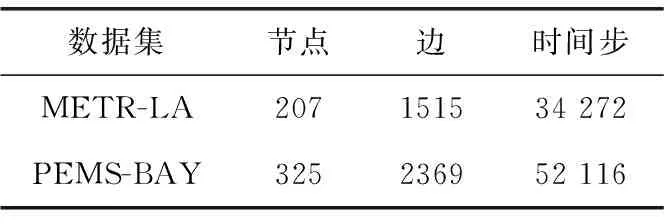
表1 数据集

2.2 基线模型及性能指标

本文模型TSDE-dGCN与其它7种基线模型进行了比较，其中包括时间序列分析模型(ARIMA)、传统机器学习模型(FNN)以及近3年来交通流预测领域中常用的深度学习模型(GWnet[10]、STAWnet[12]、DCRNN[13]、FC-GAGA[14]、Ada-STNet[15])等。

为了评估不同模型的性能，本研究采用了3种广泛使用的统计指标[10]：平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方根误差(RMSE)。

2.3 实验设置

模型训练过程中batchsize大小设置为64，优化器选用Adam，初始学习率设置为0.001，并引入学习率衰减策略，即当验证集准确率在10个周期内没有提升，则学习率衰减为原来的3/10，训练epoch都设置为100，图卷积层的最大深度设为2，扩张卷积和图卷积的信道大小设为32，动态邻接张量中的嵌入维数设置为16。

2.4 结果分析

本节将TSDE-dGCN模型与前述7种基线模型在测试集上进行12步(时间跨度一小时)的多步预测实验，并将其中15 min、30 min和60 min的预测值的评价结果列出，见表2(以数据集METR-LA为例)。我们可以观察到，基于时间序列的统计模型ARIMA以及机器学习模型FNN预测效果都较差，说明其对非线性数据的建模能力有限。后面的6种深度学习模型都同时考虑到了时空关系，可以看出性能都有了较大提升。DCRNN将GCN网络和递归神经网络以编解码的方式结合在一起构成扩散卷积递归神经网络能够有效处理时空数据，表明考虑了时空关系的深度学习模型有更好的预测效果。基于GCN的模型利用图结构来表示交通网络的非欧氏结构，这有助于它们更有效捕获交通节点之间的相关关系。此外，使用时空GCN的模型中(如GWnet、STAWnet及Ada-STNet)，GWnet受益于图卷积网络对空间依赖性建模，从数据中学习到自适应邻接矩阵，以图波网的形式传向下一个网络层；STAWnet在其基础上给每个网络层添加了注意力机制为每个节点分配权重，在步长稍大一些(如30 min和60 min)的情况下可以带来更好的性能；AdaSTNet充分考虑了图结构的动力学和自适应性，它从宏观角度(长期内稳定)和微观角度(短期内波动)自适应地推断出图形结构，这几种模型比那些只使用简单GCN的模型可以获得更好的效果。

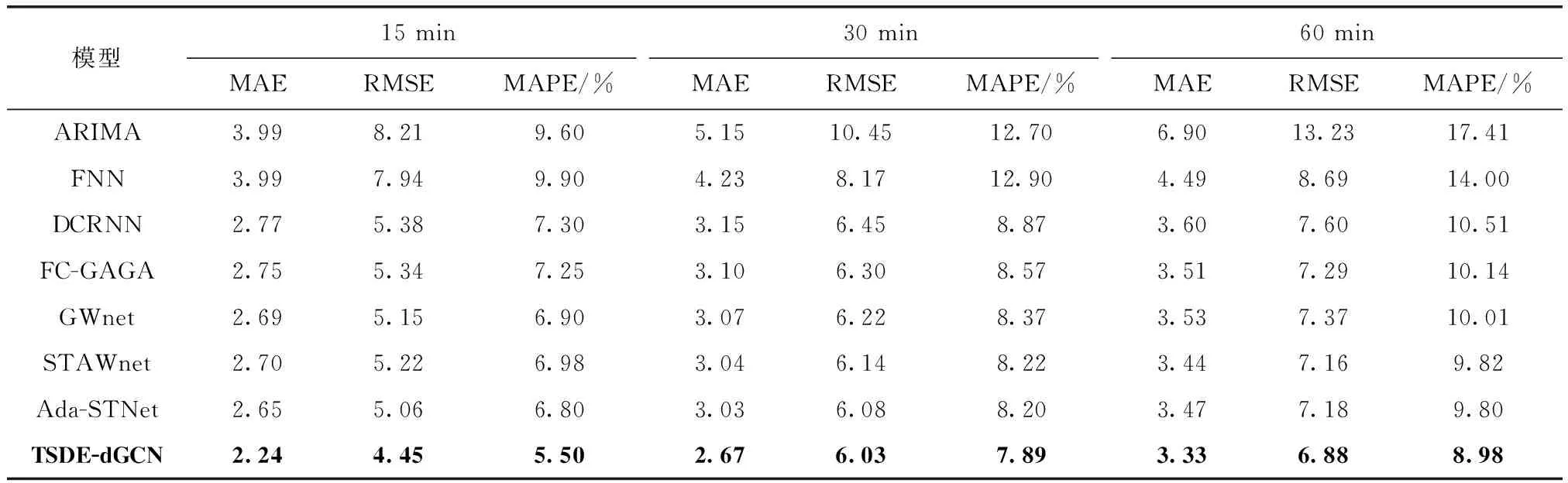
表2 各个模型在METR-LA数据集上的实验结果

本文TSDE-dGCN模型在METR-LA数据集上的3种预测步数下都取得了最优的预测结果，验证了本文模型在实现路网多步预测任务中的有效性，这可能得益于利用Deepwalk算法构建时空嵌入向量与图卷积自适应更新机制的结合有助于我们的模型捕获节点之间更微妙的相关性，同时考虑了时隙特征和空间特征的动态邻接张量可以更好地提取时空依赖性，同时整体上不同时间层次的信息流在门控机制与ST-Block块的框架下可以很好地扩散。

2.5 时空块和最大扩散步长的影响

本节对模型中的两个核心超参数进行分析，探究其对模型预测性能的影响，主要有模型整体框架中的时空块个数b和门控扩张卷积中的最大扩散步长k。

不同时空块个数对模型预测结果的影响如图8(a)、图8(b)所示，随着时空块的增加，预测误差先减小后增大。一开始时空块数的增加可以使模型能够很好地处理不同时间层次的空间依赖性(对应于b小于4之前)；但时空层数增加的同时，图卷积网络层数也在增加，深层的图卷积网络极易出现过拟合现象，会导致预测精度下降。故本文的整体预测框架中将时空块数设为4。

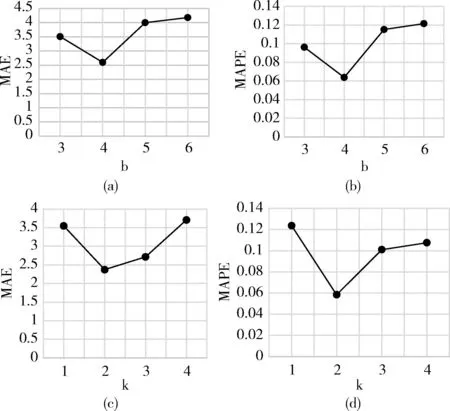
图8 不同b、k对预测结果的影响

扩散步长k对应于1.5节的dilation，其影响的是卷积网络中的感受野大小，当每层的dilation都为1时就是一般的卷积网络。图8(c)、图8(d)显示了使用不同扩散步长k时的表现，可以看出，随着最大扩散步长k的增加，预测误差也是先减小后增大。较大的k可以使模型考虑到更大范围的空间关联，但如果更大范围里的路网交通实际上与当前的路段并没有关联时，则考虑高阶相邻路段的信息可能会损害预测的精度。因此本文模型中的最大扩散步长设为2较为合适。

2.6 图结构矩阵的影响

为了验证本文模型学习到的图结构矩阵的有效性，以METR-LA数据集为例，本文将图结构矩阵进行可视化。首先验证了图结构矩阵捕获空间节点关联情况的能力，如图9所示。图9(a)为学习到的207个传感器之间的图邻接矩阵的热力图，图9(b)为对应的实际传感器分布图。以节点64-72以及88-96为例(图9(a)中矩形框框柱的部分)，可以明显看出，相比88-96那一列，64-72那一列有更多的高值点，这表明，64-72这组节点对周围的大多数节点都有影响，而88-96节点对周围的影响较弱。图9(b)证实了我们的观察结果，可以看出，88-96中部分节点位于单一道路上，附近的相邻节点较少(如节点90和92)，另一部分节点虽然附近相邻节点多，但有些是分布在相反方向的道路上(如节点88和89，91和93)，故相关性较低；而64-72这组节点中除了64、65及66以外的其它节点基本都位于几条主要道路的交叉口附近，故对周围的影响较大。

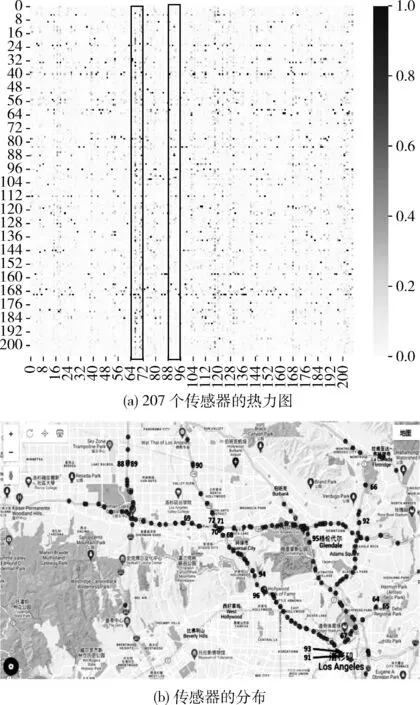
图9 207个节点的空间分布

其次，选择数据集中前50个传感器验证学习到的空间连接关系准确性，如图10(a)所示。以节点6为例，图10(a)中显示其空间依赖较大的节点有12、15、36、38，观察图10(b)实际分布图可知，节点12、17、15、5均分布在采样节点的相邻空间路段上，但其中只有节点12、15与采样节点在同一方向上，即节点12、15位于采样节点的上游，故对其影响较大；同理，节点36、38位于同一方向上的另一个路段，也会对采样节点产生较大空间影响。此外，观察图10(b)可以发现节点15和节点5虽位于公路的相反方向上，但通过观察实际加州路网发现节点5所在路段前方有一座跨线桥，可以通往节点15所在路段，故在图10(a)的热力图中，节点15对节点5也具有较强空间依赖。

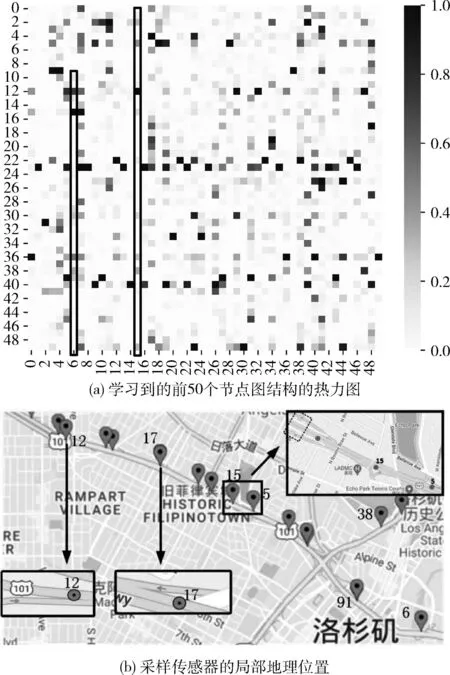
图10 图结构矩阵可视化

以上两个例子可以证实本文模型学习到的图结构矩阵可以从交通时间序列数据中自动学习节点之间的隐藏关系，在一定程度上反映了节点之间的真实空间依赖性，且具有很好的可解释性。

2.7 时间计算

本文以METR-LA数据集为例分别统计了每个深度学习模型的训练时间和演化时间，见表3。其中训练时间仅展示每个epoch运行所需要的时间，推理时间为训练好的模型应用于整个测试数据上的演化时间，都以秒(s)为单位。表3显示，DCRNN需要的时间最长，因为它完全依赖于递归网络，只能根据前面的step预测下一个step，而其它模型都是可以在单次运行中直接预测出不同horizon水平(如3(对应15 min)6(对应30 min)或12(对应60 min))的结果。由于FC-GAGA模型不涉及太多的卷积操作故花费时间最少，但其精度相比本文模型较低。GWnet和STAWnet模型运行时间相当，二者都采用图波网架构，都属于非自回归模型。在本文模型和Ada-STNet所用时间相当的情况下，本文模型的精度更高，故综合来看，本文模型在交通流预测方面有较好的性能。

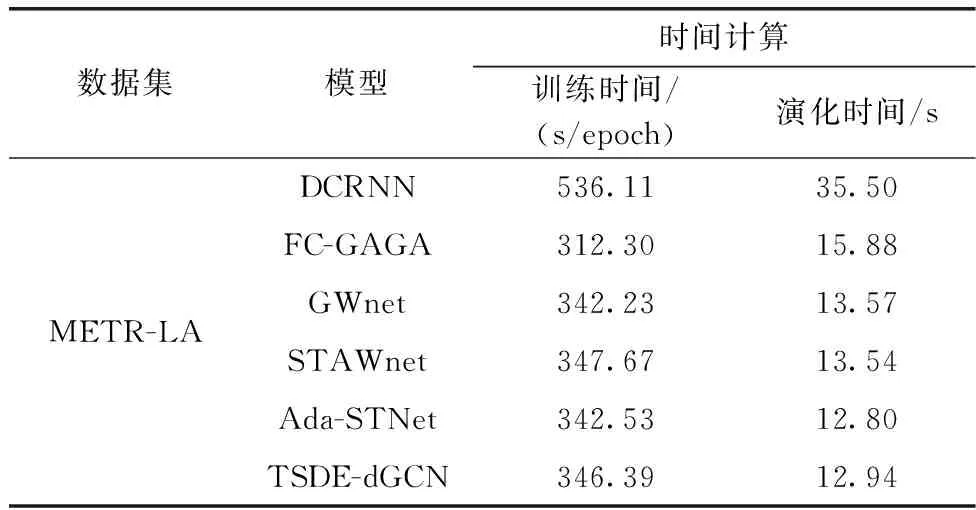
表3 不同模型运行时间计算

3 结束语

针对交通路网中复杂的动态隐式时空依赖关系，本文提出一种基于时空数据嵌入的动态图卷积预测模型。不同于多数研究中对时间依赖和空间依赖分别建模再进行融合的思想，本文模型通过将时空数据作为一个整体映射到embedding空间中，尝试将时隙特征和空间特征融合建立三维嵌入邻接张量作为卷积模块的输入图表示，并针对图卷积网络设计了一种自适应更新参数的机制。实验结果表明，本文模型学习到的图结构矩阵可反映节点间欧氏距离，能很好地识别实际路网的隐式空间特征，具有较好预测性能。