DCVAE与DPC融合的网络入侵检测模型研究

李登辉,葛丽娜,王 哲,樊景威,张 壕

(广西民族大学 人工智能学院,南宁 530006) (广西混杂计算与集成电路分析设计重点实验室,南宁 530006)

0 引 言

随着网络空间日益发展,国家和个人的隐私、财产安全也随之受到巨大威胁[1],新型网络攻击层出不穷[2],如何迅速、准确地在复杂的网络空间中检测和识别出网络攻击,并及时做出应对,成为越来越多企业所要面对的问题.入侵检测系统是信息安全综合防御系统的重要组成部分,通过监测网络流量判断是否存在入侵行为,识别出正在发生的入侵企图或已经发生的入侵活动.

由于科技发展和计算机算力提升等原因,机器学习在入侵检测领域变得更加火热[3].随机森林[4]、XGBoost[5]、决策树[6]、朴素贝叶斯[7]、支持向量机[8]等这些传统机器学习方法已经广泛应用到入侵检测系统中,均取得了不错的效果,达到了入侵检测系统高准确率和低误报率的要求,但是传统机器学习方法需要复杂的特征工程[9],选择最佳特征,才能达到理想的效果,特征选择是传统机器学习方法的重中之重.

深度学习只需将网络流量的初始特征直接传递到神经网络中,通常就可以实现良好的入侵检测效果.面对更复杂的网络环境,更庞大的网络流量,深度学习比传统机器学习更能适应不同的领域和应用[10].因此利用深度学习方法设计入侵检测系统是继传统机器学习方法后的新潮流[11].为了提升入侵检测模型的性能表现,研究人员或选择学习网络流量的概率分布,空间特征和时序特征[12],或集合多方数据构建入侵检测模型[13],增强网络流量特征的表达能力,或针对现存入侵检测领域数据集间存在特征差异大导致模型泛化能力差、缺乏可靠的评价体系等问题,提出标准数据集,以衡量训练模型的泛化能力和有效性[14].

以往的入侵检测模型主要关注点是改进特征提取能力,提高已知攻击的检测精度.当网络中产生与任何已知攻击完全不同行为模式的未知攻击时,大多数入侵检测系统会将其误分类为正常流量,产生极具误导性的信息,因此需要能够识别未知攻击的深度学习模型来帮助构建入侵检测系统[15].

入侵检测系统如果简单地将网络流量粗粒度分类为正常流量或恶意网络攻击,安全专业人员无法获得更准确的诊断信息以有效指导解决安全威胁,而细粒度分类可以获得更详细的诊断信息降低对恶意网络攻击的反应时间,减少给企业带来难以估计的损失.所以通过将判别条件变分自编码器(Discriminative Conditional Variational Auto-Encoder,DCVAE)与密度峰值聚类(Density Peak Clustering,DPC)算法[16]结合提出新的模型,相比于现在流行的方法有更好的性能表现,文章的主要贡献如下:

1)提出的模型具有检测未知攻击的能力,降低未知攻击造成的安全风险.

2)提出的模型具有细粒度分类的能力,能够帮助安全专业人员迅速判段恶意网络攻击的精准类别,并对其进行及时反应.

3)实验结果证明所提出的模型可以一定程度应对当前复杂的网络环境.

本文的其余内容安排如下.第1部分讨论入侵检测相关工作,第2部分介绍了所提出的模型涉及到的背景知识,第3部分对提出的模型进行详细介绍,第4部分展示了模型的实验结果,并与其他入侵检测模型对比,第5部分对所做工作做出总结,并指出了模型不足和未来研究方向.

1 相关工作

衡量入侵检测系统的重要特征之一是检测未知攻击的能力,未知攻击也被称为零日攻击,许多组织和研究人员对未知攻击高度关注.入侵检测中的未知攻击检测主要定义为单类问题,即只学习正常流量的行为模式,将异常网络流量识别为未知攻击.

1.1 基于传统机器学习模型的未知攻击识别

以往主要利用传统机器学习模型完成未知攻击识别,文献[17]中在物联网领域比较Kmeans、单类支持向量机(One-Class Support Vector Machine,OCSVM)、随机森林、自编码器(AutoEncoder,AE)等模型检测未知攻击的能力,发现基于机器学习的入侵检测模型即使没有未知攻击的作为训练样本,也能取得良好的检测结果.文献[18]中提出结合支持向量机与极限学习机的多层混合模型,利用支持向量机寻找正常流量与恶意网络攻击数据分布的超平面,在对网络流量进行多分类的同时具有识别未知攻击的能力.文献[19]中利用k最近邻算法寻找网络流量k个最近距离的数据,通过这些数据投票确定是否为未知攻击.文献[20]中利用决策树对已知网络攻击进行过滤,然后利用单类支持向量机对正常流量进行训练找出异常攻击.文献[21]中针对网络流量样本单一、数据维度高、相关性强、异常点多的特点,利用改进的主成分分析算法去除训练样本中的异常值,并使用粒子群算法对单分类支持向量机的参数进行优化,提高模型检测未知攻击的性能.文献[22]中采用KKT条件加强增量学习速率,提高了单类支持向量机的学习率和模型的可扩展性.文献[23]中借鉴软间隔支持向量机优化单类支持向量机的超平面,模型的误报率得到显著降低.文献[24]中利用孤立森林、局部离群因子检测的方法,探测网络流量间的局部密度,对离群的孤立点判定为恶意网络攻击.文献[25]中针对未知攻击行为特征不明显的问题,根据网络流量的统计特征构造doc-word矩阵,分析潜在语义信息,从而判断是否为未知攻击.

这些方法对未知攻击检测的性能得到一定程度提高,但传统机器学习模型在面对大量的网络流量时,不能自主学习特征从而使一部分有效特征遗漏,而且检测模型的稳定性也不高,导致不能取得更好的识别效果.

1.2 基于深度学习模型的未知攻击识别

随着计算机算力的不断提升和深度学习不断发展,入侵检测领域研究重心也逐渐从传统的机器学习转向深度学习.不同于传统机器学习模型,深度学习没有复杂的特征工程,更适合处理高维、大型数据,表达能力更强,文献[26]中对主成分分析法、孤立森林、OCSVM、AE模型在未知攻击检测中的性能进行对比,AE从计算复杂度和分类能力等方面相比于传统机器学习模型性能均有很大提升.文献[27]中改进了AE模型神经网络的隐藏层数,探索不同深度神经网络在分类时的性能表现.文献[28]中在AE中引入丢弃法来解决神经网络训练时较易发生过拟合的问题,并利用未知攻击使用正常流量训练出的单类自编码器(One-Class AutoEncoder,OCAE)重建样本时会产生更大误差的原理,达到识别未知攻击的目的.文献[29]中对OCSVM、AE、变分自编码器(Variational AutoEncoder,VAE)在未知攻击检测中的性能对比,并分析不同阈值下VAE方法的性能,实验结果表明,VAE的性能在很大程度上优于AE和OCSVM.文献[30]中利用双向生成对抗网络(Bidirectional Generative Adversarial Networks,BiGAN)平衡网络流量各类样本训练占比,同时利用BiGAN中的判别器,对超出分类结果阈值的样本判定为未知攻击.文献[31]中将BiGAN中的生成器的迭代训练与判别器的训练分离,改进生成器和判别器的性能,提高了模型识别未知攻击的能力.文献[32]中基于网络流量间的密度、距离等特征提出混合聚类方法识别网络攻击.文献[33]中利用改进的DPC算法将网络流量划分为多个子集,求出对应子集的分布,能有效识别未知攻击.文献[34]将一维卷积自编码器和OCSVM组合,定义重构误差与分类误差结合的目标函数,学习网络流量的紧凑表示.文献[35]中利用自编码器对正常流量与未知攻击进行对比学习,根据攻击数据的重建误差大于正常流量的假设,达到识别未知攻击的目的.

以上深度学习模型使用了各种方案探索提升未知攻击识别的准确率,也因为网络环境逐渐复杂,网络攻击种类逐渐增多,模型也从简单的二分类模型逐渐转变为更精细的多类分类模型,因此为了快速应对层出不穷的网络攻击,未来的入侵检测模型一定是面向未知攻击识别和细粒度分类的.

2 背景知识

2.1 DCVAE模型

DCVAE在CVAE基础上加入判别网络[37],复用训练模型中的隐变量z与原始样本x的标签y,模型如图1所示.CVAE多作为生成模型用于构建基于异常的入侵检测系统,DCVAE利用打上细粒度标签的网络流量训练判别网络,使得模型具有细粒度分类的能力.经过训练的DCVAE可以根据样本标签类别生成指定类别样本[38],被误分类的样本利用解码器生成的新样本后会比原样本产生更大的重建误差[37].因此,本文利用DCVAE得到正常流量重建误差,并利用DPC算法学习重建误差的分布,达到识别未知攻击的目的.

图1 DCVAE模型Fig.1 DCVAE model

2.2 DPC算法

DPC[39]是基于样本密度的聚类算法,不受类簇的形状和大小影响.聚类的目的是根据属性相似性将数据组织成组,使同一簇中的数据具有相似的属性,而不同簇中的数据彼此不同.其中的关键是根据簇中心的特征绘制决策图,以快速识别准确的簇中心.簇中心有两个特征:1)局部密度相对较大;2)簇中心的位置相对远离具有较高局部密度的任何其他对象.

为求出每个类簇的密度峰值,引入两个概念:基于数据点i的局部密度ρi和相对距离δi.其中对于局部密度ρi,有两种计算方式,分别是截止核和高斯核,如公式(1)和公式(2)所示:

(1)

(2)

其中dij是数据点i到数据点j的欧几里得距离,dc是截止距离.

对于截止核,数据点i的局部密度是点i的dc大小的邻域中的数据点个数.当两个数据点的dc邻域中的数据点个数相同时,两个数据点的密度数据点相等,忽略了dc邻域的数据分布因素对局部密度的影响.因此,提出了高斯核来解决这个问题.

对于相对距离δi是通过计算数据点i与其他具有较高局部密度和最近距离的点之间的欧几里得距离来计算的,δi定义为:

(3)

对于密度最大的点,取δi为最大值:

(4)

DPC算法为每个数据点定义决策值γi:

γi=ρi·δi

(5)

DPC算法选择将局部密度高而且距离远的数据点视为密度峰,即找到γi较大的点作为聚类中心,将剩余的数据点分配给距离最近的密度峰.

DPC算法在入侵检测领域的研究主要是将网络流量的密度属性加入到网络流量特征中,找到正常流量的分布特征[33],且正常流量与恶意网络攻击间使用DCVAE产生的重建误差分布有显著不同[37],因此利用DPC算法学习正常流量的分布,可以帮助识别未知网络攻击.

3 DCVAE-DPC模型

针对许多基于深度学习的入侵检测模型识别未知攻击能力不强的问题,本文提出DCVAE-DPC模型,并赋予模型细粒度分类能力,提供更准确的诊断信息,以有效指导安全人员解决安全威胁.

3.1 DCVAE-DPC模型

DCVAE-DPC模型框架如图2所示,图2(a)是DCVAE-DPC模型的训练过程,图2(b)是DCVAE-DPC模型完整的入侵检测过程.

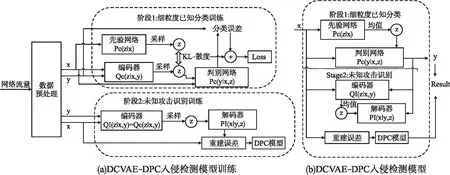
图2 DCVAE-DPC入侵检测模型Fig.2 DCVAE-DPC intrusion detection model

模型训练首先是细粒度攻击分类训练,将训练数据集预处理,打上细粒度标签,输入DCVAE模型后,使得模型分类的结果最大概率地接近真实值y,即最大化概率P(y|x).然后是未知攻击识别训练,最小化未知攻击的识别风险,利用DCVAE模型的编码器学习正常流量的固有分布z,解码器的生成样本最大概率接近x,即最大化概率P(x|y,z).利用输入实例与生成样本间的重建误差,使用DPC算法找出正常流量重建误差的分布,当输入实例的重建误差超出阈值时,即可判别为未知攻击.

模型入侵检测过程首先对输入实例x进行细粒度攻击分类,判断是y∈N={B,A1,…,Ak}中的正常流量或已知攻击,其中B代表正常流量,A1至Ak代表k种已知攻击,若实例x判断为正常流量,则进入未知攻击识别阶段,计算x的重建误差与正常流量重建误差的中心点间的距离,若超过设定阈值,则给网络流量重新打上Ak+1标签,Ak+1代表未知攻击,模型最后的输出结果是y∈N={B,A1,…,Ak+1},因此模型具有识别未知攻击的能力.

3.2 数据预处理

NSL-KDD初始数据集并不能直接用来进行模型训练,需要进行预处理:

1)数字化.NSL-KDD数据集中包含41种特征,其中有3种是字符型特征Protocol_Type、Service和Flag,分别包含3、70和11种类别的状态,因此使用one-hot编码将这些特征值进行数字化,通过one-hot编码可以将41维的特征扩展为122维.

2)归一化.经过独热编码的同一特征的特征值间差异较大,容易造成模型训练收敛速度慢,将特征值进行归一化后,可以帮助提高模型的精度,采用最大最小归一化方法将数据集中的数据变换为[0,1]区间,公式如下:

(6)

其中x是需要进行归一化的数值,x*是归一化后的数值,xmin是y所在特征中最小数值,xmax是x所在特征值中最大数值.

3.3 细粒度已知分类训练

本阶段的训练目标有两个,在训练样本集ST上,使DCVAE模型分类结果的概率最大化地接近真实值y,目标公式如公式(7):

(7)

其中x是训练样本集ST中的输入实例,y∈{0,1}k是输入实例经过独热编码后的类别标签.

同时需将学习到的隐变量z应用到未知攻击识别训练中去,所以设z的真实概率分布是PC(z|x,y),利用函数QC(z|x,y)尽可能接近z的真实分布,并利用KL散度来衡量两个分布间的距离,目标公式如公式(8)所示:

(8)

结合公式(7)、公式(8)则有公式(9):

(9)

又由公式(8)则公式(9)可以化简为公式(10):

(10)

将公式(10)重写,本阶段最终目标公式为公式(11):

(11)

由公式(11),目标公式由3部分神经网络构建,用DCVAE模型中的编码器网络来拟合概率分布QC(z|x,y),用先验网络来拟合概率分布PC(z|x),用判别网络来拟合概率分布PC(y|x,z).

公式(11)的前半部分使用高斯函数得到QC(z|x,y)和PC(z|x)分布的结果如公式(12)、公式(13)所示:

即z|x,y～N(μ1(x,y),∑1(x,y))

(12)

z|x～N(μ2(x),∑2(x))

(13)

其中(μ1,∑1)和(μ2,∑2)是两个分布的均值和方差,因此公式(11)的前半部分可以复写为公式(14):

(14)

公式(11)的第2部分可以实现为编码器网络QC(z|x,y)和判别网络PC(y|x,z)与重参数技巧的结合.也就是说,判别网络PC(y|x,z)输入的隐变量z是从编码器网络QC(z|x,y)的高斯函数中采样得到的如公式(15)所示:

(15)

由于标签y是一个由1和0组成的二值向量,使用softmax函数求得PC(y|x,z)的结果如公式(16)所示:

yi|z,x～Bernoulli(pi(z,x))

(16)

其中yi是标签y的第i个值,因此公式(11)的第2个部分可以复写为公式(17):

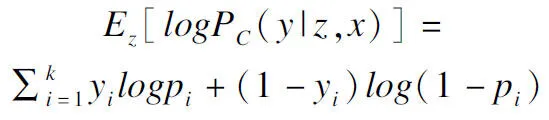
(17)

所以细粒度已知攻击分类训练阶段的损失函数公式为(18):

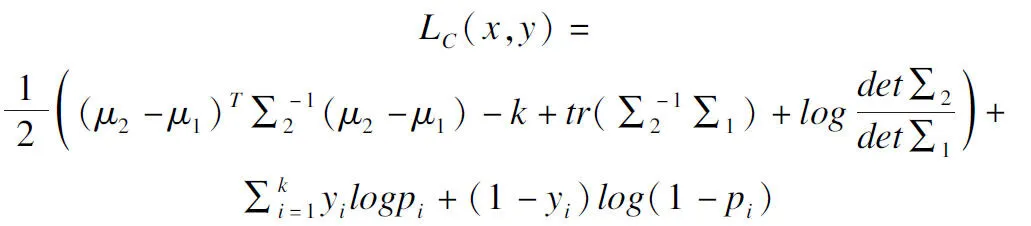
(18)

3.4 未知攻击识别训练

首先在正常流量标签条件下使解码器的生成实例概率最大化接近输入实例,目标公式为(19):

(19)

为了提升DCVAE模型解码器的表现,选择利用编码器学习到的隐变量z结合实例真实标签y得到解码器网络PI(x|y,z),所以目标函数更新为公式(20):

(20)

其中QC(z|x,y)是复用细粒度已知分类训练阶段的编码器网络,使用高斯函数拟合生成的结果,如公式(21)所示:

x|y,z～N(μ(y,z),∑)

(21)

使用μ(y,z)的均值来代表重建的实例,而∑作为方差在这里并不需要,因此上式可以复写为公式(22):

Ez[logPI]=-k‖x-μ(z,y)‖2-C

(22)

其中k,C均为常数.

所以解码器网络损失函数如公式(23)所示:

Lr(x,y)=‖x-μ(z,y)‖2

(23)

设R={r1(x1,y1),r2(x2,y2),…,rn(xn,yn)}代表正常流量的重建误差集,ri是每个输入实例xi的重建误差.

然后利用DPC算法找出正常流量的重建误差的聚类中心,并求出所有正常流量的重建误差与聚类中心间的欧式距离,如公式(24)所示:

di=‖rc-ri‖2

(24)

其中rc代表正常流量的重建误差的聚类中心,以下简称为聚类中心,di代表第i个输入实例的重建误差与rc间的距离.

被误分类的输入实例打上错误的标签后,利用解码器生成的新样本会比原样本产生更大的重建误差,设定合适的阈值e,保证正常网络流量高分类准确率的同时,使得模型具有一定识别未知攻击的能力,入侵检测模型的训练过程总结在算法1中.

算法1.训练DCVAE-DPC入侵检测系统

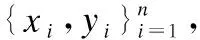
输出:训练完成的DCVAE模型,聚类中心rc,阈值e

1.对数据集进行预处理

2.首先进行细粒度已知分类训练,设置训练的epoch值E以及batch_size,则M=n/batch_size

3.for i in E do

4. for i in M do

5. 利用编码器网络QC(z|x,y)以及先验网络PC(z|x)根据公式(12)、(13)得到两个分布的均值与方差,μ1,∑1,μ2,∑2,并通过重参数化分别采样得到隐变量z

6. 将编码器网络QC(z|x,y)中采样得到的隐变量z输入判别网络PC(y|x,z),结合特征xi,得到预测类别yi*

7. 根据损失函数公式(18)更新先验网络PC(z|x),编码器网络QC(z|x,y)以及判别网络PC(y|x,z)

8. end for

9.end for

10.进行未知攻击识别训练

11.for i in E do

12. for j in N do

13. 将编码器网络QC(z|x,y)复用到未知攻击识别训练,得到编码器网络QI(z|x,y)的均值μ与方差∑,并采样隐变量z

14. 将隐变量z结合正常流量的类别标签y输入解码器网络PI(x|y,z)中,得到重建后的网络流量x*

15. 根据损失函数公式(23)更新解码器网络PI(x|y,z)

16. end for

17.end for

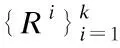
19.利用DPC算法根据重建误差计算γ值和δ值,求出聚类中心rc及阈值e

3.5 DCVAE-DPC入侵检测系统

DCVAE-DPC入侵检测系统在得到网络流量输入实例x后,首先进行预处理,然后进入细粒度已知分类部分,由先验网络PC(z|x)得到当前网络流量x服从高斯分布中的均值μ1和方差∑1,从高斯分布中采样z结合x即可利用判别网络PC(y|x,z)得到这一阶段的分类结果如公式(25)所示:

(25)

其中z=E[z|x]=μ1,由于细粒度已知分类阶段会将未知攻击误分类为正常流量,所以在未知攻击识别阶段将x与网络流量的预测标签y*,输入到编码器网络QI(z|x,y)中采样z,然后从解码器网络PI(x|y,z)中得到重建后的网络流量x*,如公式(26)所示:

x*=PI(x|y*,z)

(26)

其中z=E[z|x,y*]=μ2.

利用在训练阶段求得的正常流量的聚类中心rc,计算输入实例的重建误差与rc的距离d,当超过预定的阈值e后,即可判定为未知攻击.

DCVAE-DPC入侵检测系统的完整检测过程如算法2所示.

算法2.DCVAE-DPC入侵检测系统

输入:网络流量特征x

输出:网络流量的预测标签y

1.在已知攻击识别阶段,利用先验网络PC(z|x)采样得到网络流量的隐变量z

2.将z与x结合输入判别网络PC(x|z)得到网络流量的预测标签y*

3.若网络流量被判定为正常流量,则进入未知攻击识别阶段,输入解码器网络PI(x|y,z),重建网络流量得到x*

4.计算得到重建误差r=x-x*

5.计算重建误差与聚类中心rc的距离d=rc-r

6.将d与预设阈值e进行对比cmp(d,e)

7.对超过e的网络流量判定为未知网络攻击,结合预测标签y*得到最终的预测结果y

4 实验结果

4.1 评价标准

对提出的入侵检测系统模型进行评估,使用准确率、精确率、回归率、F1-score作为评估指标:

准确率(Accuracy):正确分类正样本和负样本的比率,如公式(27)所示:

(27)

其中P代表正样本数量,N代表负样本数量.

精确率(Precision):识别出的样本中正例占的比率,如公式(28)所示:

(28)

回归率(Recall):样本所有真正的正例中,识别正确的正例所占的比率,如公式(29)所示:

(29)

F1-score:精确率和召回率的调和平均值,F1 score越高,说明模型越稳健,如公式(30)所示:

(30)

4.2 实验数据集设置

NSL-KDD数据集[40]:KDD CUP99数据集中大约78%和75%的网络数据包在训练和测试数据集中重复,于是对KDD CUP99数据集中的冗余数据进行了清洗,合理的选择训练集和测试集的记录数量,使得实验数据无需因为数据量过大而进行随机选取,保证了不同研究工作的评价结果具有一致性和可比性.NSL-KDD的训练数据集中包含有大约12万个样本,测试数据集包含有大约2万个样本,NSL-KDD数据集包含拿了4种主要类型的攻击分别是Dos、Probe、R2L、U2R,并且数据集中初始特征有41种.

为了实现细粒度攻击分类,DCVAE-DPC模型选择使用细粒度标签,将标签细化,NSL-KDD数据集中将Dos攻击细化为Back、Land、Neptune、Pod、Smurf、Teardrop,Probe攻击细化为IPsweep、Portsweep、Nmap、Satan,R2L攻击细化为FTP Write、Guess Password、Imap、Multihop、Phf、Spy、Warezclient、Warezmaster,U2R攻击细化为Rootkit、Buffer Overflow、LoadModule、Perl.为了测试提出的模型的表现,在NSL-KDD数据集中,随机抽取80%的数据作为训练数据集,20%的数据作为测试数据集,为了测试DCVAE-DPC模型未知类型攻击识别的效果,选择测试数据集作为未知攻击,未知攻击不参与模型的训练阶段,只会参与到模型的测试阶段.

4.3 实验参数设置

DCVAE-DPC模型的在细粒度已知分类训练中,输入层有122维网络流量特征和9维类别标签,先验网络、编码器网络、判别网络均采用多层神经网络结构,隐藏层均为100,60,20个神经元,其中编码器网络利用KL散度帮助拟合出先验网络,得到具有类别特征的隐变量为3维,不仅可以输入到判别网络帮助提高网络流量识别准确率,也可在未知攻击识别阶段输入解码器网络帮助生成特定类别的网络流量,判别器网络接收到网络流量特征输入和隐变量共125维,输出层的结果为经过softmax函数的9维类别标签.

在未知攻击识别训练中,解码器网络输入层为122维网络流量特征和正常流量类别标签,隐藏层为五层神经网络结构,分别有500,1000,800,600,200个神经元,输出结果为重建后的网络流量为122维.

模型训练时把所有训练数据完整训练一次为一个轮次(epoch),轮次的大小对模型分类准确率有很大的影响,随着轮次的增加,当epoch设置为200,batch_size设置为100,学习率设置为0.001时,DCVAE-DPC模型的准确率逐渐升高,并趋于稳定.

4.4 实验结果分析

在实验仅有未知攻击识别阶段时,通过DCVAE模型计算正常流量的重建误差,并利用DPC算法寻找重建误差的聚类中心点rc,结果如图3所示,选取图中γ值和δ值均大的点作为聚类中心,图中有一个点符合要求,因此可以确定为中心点rc.

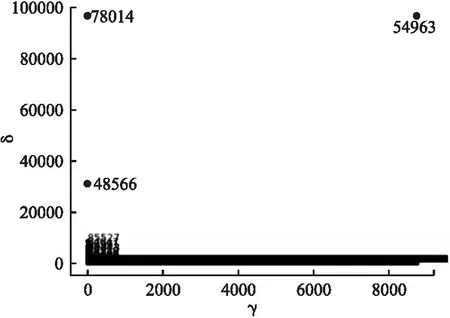
图3 利用DPC算法求出正常流量重建误差中心点rcFig.3 Using DPC algorithm to find the reconstruction error center rc of normal network traffic

求得测试集样本与重建误差中心点rc间的距离,结果如图4所示,其中浅灰色直方图代表正常流量重建误差的分布,浓灰色直方图代表未知攻击重建误差的分布.

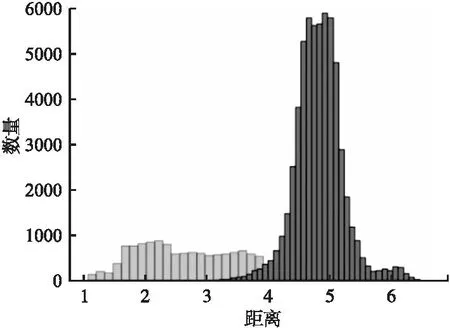
图4 正常流量和未知攻击重建误差与rc距离分布Fig.4 Reconstruction error distance distribution of normal network traffic and unknown attacks with rc

由图4可知,在NSL-KDD数据集中正常流量的重建误差与中心点rc之间的距离大多集中在0～4之间,而未知攻击大多集中在4～6之间,所以设定好合适的阈值,将超过阈值的网络流量打上未知攻击的标签,即可识别出未知攻击.

设定不同阈值e后,模型的分类表现结果如表1所示,其中取阈值为3.9时,模型的表现最好.

表1 不同阈值e下DCVAE-DPC模型分类表现Table 1 Classification performance of DCVAE-DPC model under different threshold e

模型分类结果如图5所示,其中混淆矩阵中的行表示真实标签,列表示预测标签,颜色越深的区域表示预测结果越集中,混淆矩阵对角线上的区域颜色越深代表分类准确率越高.可以看到只经过未知攻击识别阶段时,DCVAE-DPC模型已经将未知攻击从正常流量中分离开,但是对正常流量的分类准确率较低,只有91%,因此模型可能会导致较高的误报率,所以需要细粒度分类阶段帮助提高模型的分类准确率.

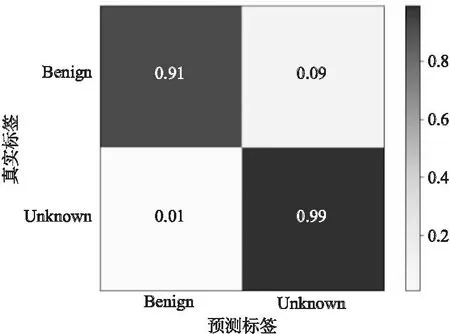
图5 未知攻击识别结果混淆矩阵Fig.5 Confusion matrix of unknown attack identification result

在实验中加入细粒度已知分类阶段后,预设Back攻击和R2L攻击为未知攻击,在NSL-KDD数据集上测试阶段分类结果的混淆矩阵如图6和图7所示,从图6中可以看出,模型在细粒度已知分类阶段实现了很高的分类准确率,对于NSL-KDD数据集,Ipsweep、Namp、Portsweep、Satan攻击均为Probe类型的攻击,Neptune、Smurf、Teardrop攻击均为Dos类型的攻击,相比于只进行Probe攻击与Dos攻击的粗粒度分类,DCVAE-DPC模型在更细分的领域最高能达到100%的准确率.由于模型没有未知攻击的先验知识,只能将未知攻击分类为正常流量或已知攻击.从未出现过的未知攻击在细粒度已知分类阶段被误分类是正常现象.

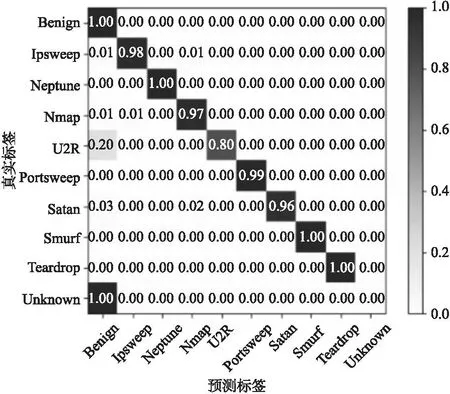
图6 细粒度已知分类结果混淆矩阵Fig.6 Confusion matrix of fine-grained known classification result

图7 细粒度已知分类+未知攻击识别结果Fig.7 Fine grained known classification and unknown attack identification result

从图7中可以看出,经过细粒度分类阶段后,在未知攻击识别阶段不仅对正常流量的分类达到97%准确率,而且对未知攻击的识别也达到了较高的准确率.

因此DCVAE-DPC模型有大多数深度学习模型没有的未知攻击识别的能力,并可以经过细粒度分类可以给安全人员提供更准确的诊断信息,以有效指导解决安全威胁,可以应对当前复杂的网络环境.

4.5 比较分析

入侵检测领域流行的研究方法中基于深度学习的方法占比较高,DCVAE-DPC模型通过学习正常流量的隐空间表示,生成更具偏向性的样本,未知攻击在以正常流量建模的自编码器中生成样本会产生更大的重建误差,因此DCVAE-DPC模型通过其他自编码器模型少有的对重建误差的再学习,找到正常流量的分布,在未知攻击识别中取得了更好的效果.

将DCVAE-DPC模型与入侵检测领域未知攻击识别的流行方法在NSL-KDD数据集中对比,结果如表2所示,可以发现,所提出的DCVAE-DPC模型与这些流行方法相比,DCVAE-DPC模型各项性能参数都达到了更优的效果,其中模型分类准确率更是达到了97.08%,且具备了大多数深度学习模型都没有的细粒度分类的能力.

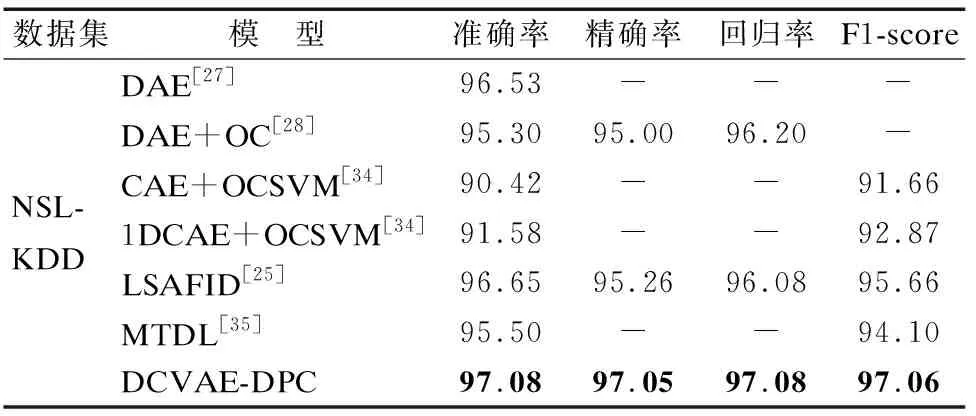
表2 DCVAE-DPC模型与流行模型实验结果对比Table 2 Comparison of experimental results between DCVAE-DPC model and state-of-art models

所以DCVAE-DPC模型比其他的流行方法在面对复杂网络环境时具有更强的竞争力.

5 总 结

针对当前入侵检测系统识别未知攻击能力不够的问题,且面对当前复杂网络环境需要及时应对网络攻击,结合DCVAE和DPC提出了入侵检测模型DCVAE-DPC.

该模型利用DCVAE增加正常流量与未知攻击间的特征区分度,并对网络流量进行细粒度分类,获得更精准的攻击诊断信息,并利用DPC找到正常流量的重建误差的分布,从而使模型能够识别未知攻击.

实验结果表明,DCVAE-DPC模型具有更高的未知攻击识别率,同时能够保证细粒度攻击分类的高准确率,与流行入侵检测模型比较,显著提高了入侵检测的性能,具有更高的性能表现.但是由于实验数据集存在数据不平衡,初始特征表达能力不够强,导致对少数类恶意网络攻击检测率仍有待提高,需进一步研究.