均衡相似程度和紧密程度的局部社区发现算法
张霄宏,吴凤祥,贾会梅,罗军伟
1(河南理工大学 计算机科学与技术学院,河南 焦作 454000) 2(河南理工大学 软件学院,河南 焦作 454000) 3(河南中光学集团有限公司,河南 南阳 473003)
0 引 言
现实世界中的很多系统都能抽象成复杂网络[1].复杂网络往往具有社区结构.同一社区内的节点连接紧密,不同社区内的节点连接相对稀疏.研究复杂网络的社区结构有助于理解网络的功能和特性,具有十分重要的理论和应用价值[2-5].局部社区发现算法因不需要了解网络的全局信息、时间复杂度较低而备受关注.局部社区发现方法可分为局部扩展优化[6,7]、派系过滤[8,9]、标签传播[10,11]以及局部边聚类优化[12-14]4类.其中,基于局部扩展优化的社区发现方法不仅能有效揭示网络的社区结构,而且划分结果稳定[15].
基于局部扩展优化的社区发现方法分为种子节点选取和局部社区扩展两个阶段.在种子节点选取阶段,可根据随机策略[16]、节点排名[17,18]以及极大团[8,9]等选择出种子节点.然而如果种子节点选择不当,则会造成社区划分不合理的后果.为了应对这一问题,文献[19-24]提出构建种子社区并从种子社区开始社区扩展的方法.在社区扩展过程中,现有的方法往往根据某个优化函数融合邻居节点.常见的优化函数有模糊关系函数[13]、相关度函数[25]、中心度函数[26]、模块度函数[27]、适应度函数[18]等.然而,比起不同社区中的节点,同一社区内的节点之间的相似程度更高.上述方法在构建种子社区和进行社区扩展的过程中并没同时考虑节点间连接的紧密程度和相似程度,不可避免的会存在社区划分合理性问题.此外,在社区扩展过程中,现有方法往往采用贪婪的策略,逐步融合最优的邻居节点,制约了算法的收敛速度.
针对基于局部扩展优化的社区发现方法在社区划分结果合理性和收敛速度方面存在的问题,本文提出了一种均衡的局部社区发现算法,均衡考虑节点间的相似程度和连接的紧密程度进行社区扩展.该算法在选定种子节点的基础上,结合相似程度和连接的紧密程度构建种子社区,以种子社区作为初始社区以迭代的方式对它进行扩展,直至收敛.本文的主要贡献有以下几点:
1)本文提出了一种种子社区构建算法,该算法根据种子节点及其连通节点之间的相似程度和连接紧密程度构建种子社区,保证了种子社区的质量,提升了社区划分的合理性.
2)本文提出了一种两级节点筛选机制,该机制均衡考虑相似程度和连接紧密程度筛选最适宜与社区合并的节点,缓解了因合并不恰当节点造成的社区划分不合理问题.
3)本文提出了一种宽容的节点合并策略,可以在一次迭代中将多个节点合并到社区,提高了社区扩展过程的收敛速度.
1 问题分析
在本文中,复杂网络用无向无权图G=(V,E)来表示.V为节点集合,且V={vi|i=1,2,…,n},n为节点总数;E为边集合,且E={(vi,vj)|vi∈V,vj∈Vandi≠j}.
基于局部扩展优化的社区发现方法首先按照一定的策略选择种子节点,然后从种子节点出发,根据预先定义的优化函数以迭代的方式融合邻居节点,直至收敛,形成社区.然而,如果种子节点选择不当,将会降低社区划分结果的合理性.针对这一问题,有学者提出在种子节点的基础上构建种子社区,从种子社区出发进行社区扩展.而社区具有社区内部的节点连接紧密,而社区之间的节点连接相对稀疏的特点.比起不同社区中的节点,同一社区内的节点更加相似.现有的方法在构建种子社区以及社区扩展过程中并没有从社区的角度出发,同时考虑社区内部节点连接的紧密性和节点间的相似性,因而不可避免的会出现社区划分结果不合理的问题.
此处,以社区扩展过程为例说明在只考虑社区内部节点连接的紧密程度或者节点间的相似程度单个因素的情况下社区划分结果的不合理问题.在只考虑社区内部节点间相似程度的情况下,社区的划分结果如图1(a)所示.在这个划分结果中,尽管v0和vs与v1,v2,v3,v4连接紧密,但是却被划分到不同的社区.在只考虑社区内部节点间连接紧密程度的情况下,社区的划分结果如图1(b)所示.尽管v6与v7,v8,v9,v10,v11连接紧密,但是却被划分到不同的社区.上述这两种划分结果显然是不合理的.
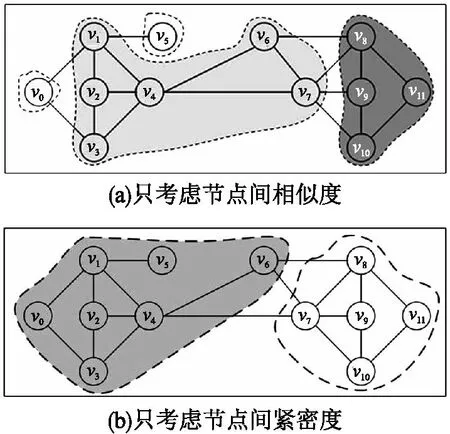
图1 社区划分分析Fig.1 Analysis of the community division
贪婪扩展是最常用的一种社区扩展方法,它以迭代的方式将优化函数最优值对应的节点并入当前社区.假设优化函数最优值对应的节点只有一个,以图2(a)所示的网络为例,则要经过5轮迭代社区扩展过程才能收敛.以图2(b)所示,如果在每轮迭代中可以合并多个节点,则经过2轮即可收敛.显然,每次只合并优化函数最优值对应的节点会制约社区扩展过程的收敛速度.

图2 迭代次数分析(Ci表示第i轮迭代生成的社区)Fig.2 Analysis of iterations( Ci represents the community generated by i round iteration)
2 均衡相似程度和紧密程度的局部社区发现算法
针对基于局部扩展优化的社区发现方法在社区划分结果合理性和收敛速度方面存在的问题,本文提出了一种新的局部社区发现算法,通过均衡考虑节点间的相似程度和连接的紧密程度进行社区扩展.该算法在选定种子节点后,首先结合相似程度和连接的紧密程度构建种子社区,然后以种子社区作为初始社区以迭代的方式进行扩展,直至收敛.在扩展过程中,提出了节点的两级筛选机制,利用该机制将在相似程度和连接紧密程度两方面优势均衡的节点作为最佳的节点,合并到当前社区,以提高社区划分结果的合理性.两级筛选机制允许在一次迭代过程中合并多个节点,以提高社区扩展的收敛速度.
2.1 种子社区生成
本文方法拟通过同时考虑节点间的相似程度和连接的紧密程度构建种子社区,来消除由种子节点选择不当引起的社区划分结果不合理问题.在构建种子社区时,首先要计算种子节点与其连通节点的相似程度和连接的紧密程度.根据“物以类聚,人以群分”的道理,本文从邻居节点的角度衡量某个节点与种子节点间的相似程度.具体来讲,本文认为两个节点拥有的共同邻居越多,这两个节点越相似,反之亦然.基于此,本文引入了式(1)计算节点的相似程度.在该式中,v表示种子节点,v1表示v的某个连通节点,ds(vi,v)表示vi和v的相似程度,N(vi)和N(v)分别表示vi和v的邻居节点集合.
(1)
种子社区的构建过程就是种子节点不断地与其连通节点合并的过程.在种子节点和某个节点合并后,种子节点和已合并节点就构成了一个整体.在后续节点的合并过程中,只考虑和种子节点的相似程度是不合理的,应当考虑和这个整体的相似程度.为便于计算和这个整体的相似程度,引入了超级节点来描述这个整体.
定义1.超级节点:种子节点和某个或者某些节点合并后,由这些节点和这些节点间的连边构成的子图称为种子社区构建过程中的超级节点.
引入超级节点后,从超级节点外部连接到超级节点内部某个节点的边,最后要变换为连接到超级节点的边.某个节点和超级节点间的相似程度仍然可以用式(1)计算,只需要用超级节点替换公式中的种子节点,用超级节点的邻居节点集合替代公式中种子节点的邻居节点集合.对于超级节点包含的各个节点,其邻居节点有可能在超级节点内部,也有可能在超级节点外部.超级节点的邻居节点集合由在超级节点外部的这些邻居节点构成.
在构建种子社区的过程中,除了考虑相似程度,还应当考虑紧密程度.本文认为,节点间的连边越多,它们之间的连接越紧密.故而,从节点间的连边入手衡量节点间的连接紧密程度.给定节点v′,∀vi∈V,且v′≠vi,记dc(vi,v′)表示v1和v′之间连接的紧密程度,由式(2)计算.在该式中,V′表示超级节点中各节点构成的集合.
(2)
为了能同时根据节点间的相似程度和连接的紧密程度构建种子社区,引入了J因子,从相似程度和连接的紧密程度两个角度度量某个节点适宜加入种子社区的程度,也就是适宜与种子节点或者超级节点合并的程度.∀vi∈V,vi与种子节点或超级节点v′的J因子根据式(3)计算.J因子越大,越适宜与种子节点或者超级节点合并.
J(vi,v′)=dc(vi,v′)·ds(vi,v′)
(3)
在构建种子社区时,只根据J因子决定是否将一个节点与种子合并.根据影响力传播的三度分割原理,在所有的连通节点中,一个节点和它三跳范围内连通的节点关系更为密切.基于此,本文方法只考虑与种子节点的距离不超过三跳的连通节点.在构建种子社区的具体过程中,按照与种子节点的距离依次遍历这些连通节点.在第1轮遍历中,只访问与种子节点距离为一跳的各连通节点,分别计算各连通节点与种子节点的J因子,将最大J因子对应的节点与种子节点合并,形成超级节点.在第2轮和第3轮遍历中,分别访问与种子节点距离为二跳和三跳的各连通节点,分别计算这些连通节点与对应超级节点的J因子,将J因子最大的节点与超级节点合并.
超级节点最终演变为种子社区.超级节点形成后,可能会出现某个连通节点与超级节点的因子大于该节点与种子节点的J因子.鉴于这一情况,在第2轮和第3轮遍历中应考虑超级节点的邻居节点,即与超级节点有直接连边的节点.综上,本文方法构建种子社区的过程如算法1所述.
算法1.种子社区构建
输入:网络G=(V,E),种子节点seed
输出:种子社区Cseeds
1.Vseeds={seed}
2.h←1,Δ←3
3.whileh≤Δ
4.rnodes←与种子节点距离为h的连通节点;
5.If(h==1)
6.计算rnodes中各节点与seed的J因子
7.最大J因子对应的节点与种子节点合并生成超级节点
8.else
9.neinodes←获取当前超级节点的邻居节点
10.将仅在neinodes中出现的节点加入rnodes
11.计算rnodes中各节点与当前超级节点的J因子
12.将最大J因子对应的节点加入超级节点
13.end if
14.End while
15.ReturnCseeds
2.2 第1级节点筛选
为了在社区扩展过程中同时考虑节点与社区间的相似程度和连接的紧密程度,本文根据前文定义的因子逐步合并邻居节点直至收敛.如果一个节点是社区内部的节点,它的所有邻居节点都在社区内部.如果是社区的边界节点,它的一部分邻居节点在社区内部,另一部分邻居节点则在其它社区.在进行社区扩展时,应尽量避免合并可能是边界的节点.因此,在进行社区扩展时没有必要去尝试合并每个邻居节点.基于此,本文引入了对节点的第1级筛选.
第1级筛选的目标是将大概率不属于给定社区的节点排除在给定社区可能合并的节点范围之外.为了达到这一目的,引入了归属度,利用归属度来判断某个邻居节点属于给定社区的概率.∀vi∈V,vi相对于给定社区的归属度记为db(vi,C),根据式(4)计算.在该式中,Vc表示社区C的节点集合.当db(vi,C)的值大于等于给定阈值θb时,认为vi可能属于社区C;否则,认为vi不可能属于社区C.
(4)
Vmerge(C)={vi|vi∈N(C) anddb(vi,C)≥θb}
(5)
在节点归属度的基础上,引入了可合并节点集合.在迭代扩展过程中,社区只能融合可合并节点集合中的节点.记给定社区C的可合并节点集合为Vmerge(C),由式(5)表示.在该式中,N(C)为社区C的邻居节点集合.由式(5)中的条件db(vi,C)≥θb可知,不可能属于社区C的节点被排除在可合并节点集合之外,从而实现了第1级筛选的目标.算法2展示了可合并节点集合的构建过程.
算法2.可合并节点集合
输入:网络G=(V,E),当前正在扩展社区C,阈值θb
输出:可合并节点集合Vmerge
1.Vmerge=Ø
2.neinodes←C的邻居节点
3.for eachnodeinneinodes
4.计算db(node,C)
5.ifdb(vi,C)≥θb
6.Vmetge=Vmerge∪{node}
7.end if
8.end for
9.ReturnVmetge
2.3 第2级节点筛选
为了能根据节点间的相似程度和连接的紧密程度划分社区,本文方法在社区扩展过程中仍根据J因子来选择可以合并的节点.在社区扩展过程中,J因子由节点和社区的相似程度以及节点与社区连接的紧密程度共同决定.∀vi∈V,vcur表示正在扩展的社区Ccur对应的超级节点.在ds(vi,vcur)较小,也就是vj与当前扩展社区相似度较低的情况下,如果dc(vj,ccur)足够大,也就是vj与当前社区连接的紧密程度足够大,那么J(vj,ccur)也较大,从而使得vj与当前扩展社区合并.在dc(vj,vcur)较小的情况下,如果ds(vj,vcur)足够大,也会使得vj与当前社区扩展社区合并.前一种情况相当于在社区合并过程中过于强调紧密度,后一种情况则相当于过于强调相似度.
这两种情况都与本文均衡考虑相似程度和连接紧密程度的初衷相悖.基于此,本文提出了第2级节点筛选.第2级节点筛选的目标是从可合并节点集合中筛选出上述两种情况涉及到的节点,将它们从可合并节点集合中删除,并从可合并节点集合中选择相似程度和连接紧密程度都能兼顾的节点,也就是相似程度和连接紧密程度均衡的节点,合并到当前社区.基于此,本文引入了以下均衡性判定策略:
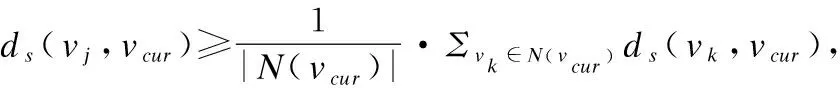
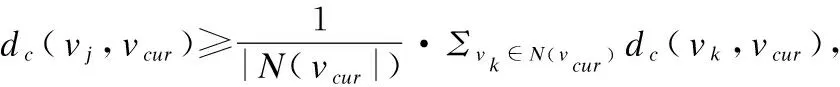
按照均衡性判定策略1-2对Vmerge(C)的节点进行筛选后,Vmerge(C)中保留的节点就是相似程度和连接紧密程度均衡的节点.为了提高社区扩展过程的收敛速度,本文引入了如下的合并策略.该策略通过允许在一轮迭代中合并满足条件的多个节点,来提升合并过程的收敛速度.

通过执行均衡性判定策略1-2可以保证将相似程度和连接紧密程度都比较高的节点合并到当前扩展社区,可以实现第2级筛选的目标.贪婪策略在每轮迭代扩展过程中只合并优化函数最大值对应的节点,限制了算法的收敛速度.与贪婪策略不同,本文提出的合并策略在每轮迭代过程中将满足合并条件的多个节点都合并到当前社区中,以此来加快社区扩展过程的收敛速度.根据上述策略,本文方法扩展社区的过程如算法3所示.
算法3.社区扩展
输入:网络G=(V,E),种子节点Seed
输出:局部社区Ccur
1.Ccur←Cseeds
2.Vcda←为Ccur创建可合并节点集合
3.Jsum=0
4.WhileVcda≠Ø
5.dcresults←计算Vcda中每个节点与Ccur的紧密度
6.dsresults←计算Vcda中每个节点与Ccur的相似度
7.dsave←计算平均相似程度
8.dsave←计算平均紧密程度
9.for eachnodainVcda
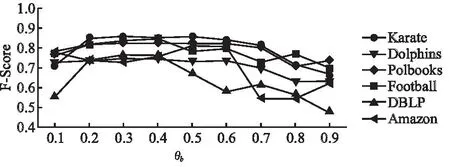
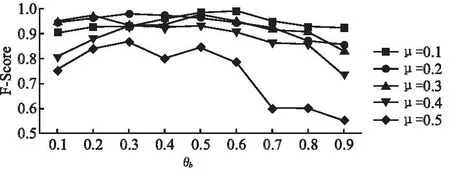
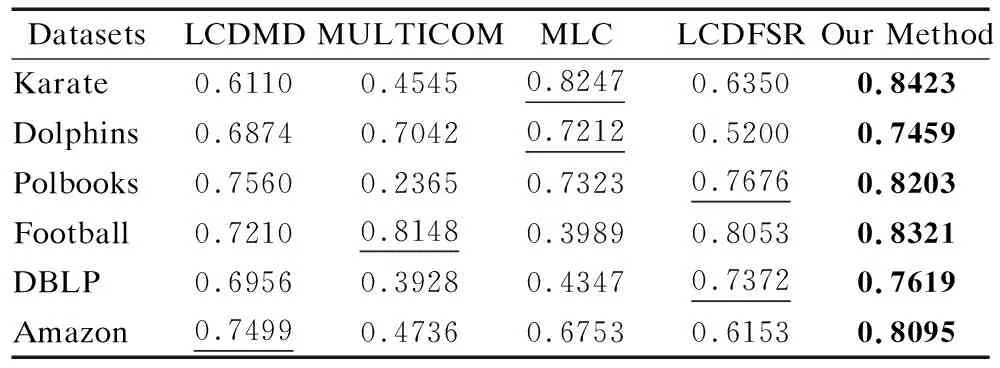
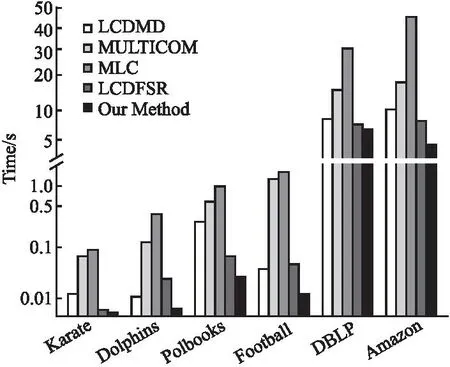
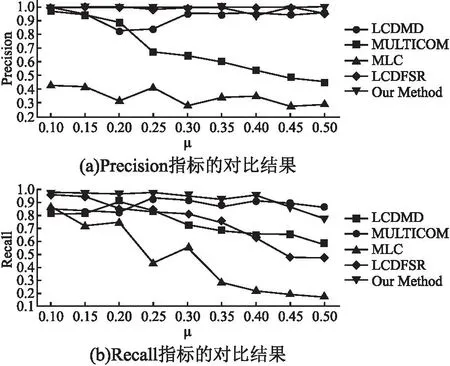
10.Ifds(node,vcur) 11.从Vcda中删除node 12.else 13.计算node与ccur的J因子 14.Jsum←node与Ccur的J因子+Jsum 15.End if 16. End for 17. IfVcda!=Ø 18.Jave←计算Vcda节点与Ccur的J因子平均值 19.else 20. break 21. for eachnodeinVcda 22.ifJ(node,vcur)≥Jave 23.将node合并到Ccur 24.End if 25. End for 26.Vcda←为Ccur创建可合并节点集合 27.End while 28.ReturnCcur 假设网络中节点的平均度为d,算法迭代t次检测完整社区.本文算法主要分为种子社区生成和种子社区扩展两个阶段.在种子社区生成阶段,假设超级节点的邻接节点在种子节点三跳之内的节点个数为q,当h为1时计算给定种子节点与邻接节点的J因子值的时间复杂度为O(d);当h不为1时计算超级节点和其符合条件邻居节点的J因子值的时间复杂度为O(q).因此,种子社区生成的时间复杂度为O(d+q).在种子社区扩展阶段,引入节点两级节点筛选机制.在第1级种子节点筛选,根据归属度筛选社区的邻居节点,假设社区的平均邻接节点个数为m,则第1级节点筛选的时间复杂度为O(m);假设经过第1级节点筛选,可合并节点集合中的节点个数为k,则在第2级节点筛选阶段中,计算可合并节点集合中各个节点与当前计算社区相似程度和连接紧密程度的时间复杂度都为O(k),按照均衡判定策略筛选遍历各个节点的时间复杂度为O(k).假设按照均衡判定策略筛选后可合并节点集合的节点个数为n,按合并策略遍历该集合中节点的时间复杂度为O(n),筛选满足融合社区节点的时间复杂度为O(n).由于满足合并策略的节点属于可合并候选集k≥n,即,则第2级种子节点筛选的时间复杂度为O(k).因此,种子社区扩展阶段的时间复杂度为O(m+k).综上所述,本文算法的时间复杂度约为O(t(d+q+k+m)). 为了验证本文算法的正确性和有效性,在多个真实数据集和人工数据集上与LCDMD算法[16]、LCDFSR算法[28]、MULTICOM算法[29]、MLC算法[30]进行了对比实验.实验中用到的操作系统为行Win10,处理器为Intel(R)Pentium(R)CPU G4600 @ 3.60GHz,内存容量为16GB.所有算法由python语言实现. 在实验过程中选取了6个真实数据集和9个人工数据集,这些数据集的社区结构都是已知的. 1)真实数据集 Karate网络[31]是根据一个空手道俱乐部成员间的关系创建的社交网络,包含34个节点和78条边,共分成2个社区.Dolphins网络[32]由海豚之间交互行为构成的社交网络,包含62个节点和159条边,共分成2个社区;Polbooks网络[33]是根据美国政治书籍网络,包含105个节点和441条边,共分成3个社区;Football网络[34]是根据足球比赛构建的网络,包含115个节点和616条边,共分成12个社区;DBLP网络[35]是一个科学家合作网络,该网络包含317080个节点和1049866条边,共分成13477个社区;亚马逊网络[35]是一个关于在亚马逊网站上销售产品的网络,该网络有334863个节点和925872条边,共分成75149个社区. 2)人工数据集 人工数据集根据Lancichinetti等人[36]提出的LFR基准网络生成.在生成过程中,参数配置如下:N=10000,k=17,maxk=3,minc=20,maxc=70,μ从0.1开始取值,每次递增0.05,直到μ=0.5,共生成9个人工网络.μ值越大,给对应网络划分社区的难度越大.故而,在实验中μ的最大值只取到0.5. 由于Karate、Dolphins、Polbooks、Football和人工网络数据集中包含的节点数较少,在实验过程中将这些数据集中的每一个节点都视作种子节点,分别从各个种子节点出发进行社区划分.而DBLP和Amazon数据集中包含的节点数较多,在实验过程中随机从每个数据集中选取10000个不同的节点作为种子节点,分别从每个种子出发进行社区划分. 本文采用调和均值F-Score[15]作为评价指标,来评估本文方法的正确性和有效性,这个指标根据式(6)计算.在式(6)中,Precision是查准率,表示被正确划分的节点占所有实际划分节点的比例;Recall是查全率,表示被正确划分的节点占真实划分节点的比例.Precision和Recall分别根据式(7)和式(8)来计算.在式(7)和式(8)中,CT表示由种子节点所属真实社区中节点构成的集合,CF表示由算法检测出的种子节点所属社区节点构成的集合. (6) (7) (8) 本文方法在第1级节点筛选过程中需要计算各邻居节点相对于给定社区的归属度,根据计算结果和预设的阈值θb把大概率不属于给定社区的邻接节点排除在外.本文通过实验的方法设置θb的取值.令θb从0.1开始取值,每次递增0.1,共取9个不同的值.分别在θb取不同值时,对各个数据集进行社区划分,并根据划分结果计算θb取不同值时算法在不同数据集上的F-Score平均值,结果如图3和图4所示.综合考虑各个数据集上的结果,在本次实验中θb的值设置为0.4. 图3 θb取不同值时本文方法在真实数据集上的结果Fig.3 Experimental results with different values of θb on the real datasets 图4 θb取不同值时本文方法在人工数据集上的结果Fig.4 Experimental results with different values of θb on the artificial datasets 图5展示了各算法在真实数据集上的对比结果.图5(a)展示的是各算法Precision指标平均值的对比结果.由此图可知,本文算法在Karate、Polbooks、Football和Amazon数据集上的Precision指标平均值在所有算法中是最高的,在Dolphins和DBLP数据集上的Precision指标平均值仅分别高于LCDFSR算法和MLC算法. 图5 在真实数据集上的实验结果Fig.5 Experimental results on the real datasets 图5(b)展示的是各算法Recall指标平均值的对比结果.由此图可知,本文算法在Dolphins、DBLP和Amazon数据集上的Recall指标平均值在所有算法中是最高的,在Polbooks数据集上的Recall指标平均值仅次于LCDFSR算法,在Karate数据集上的Recall指标平均值高于LCDMD算法和MULTICOM算法,在Football数据集上的Recall指标平均值高于LCDMD算法和MLC算法. 表1展示了各算法在真实数据集上F-Score指标的平均值,最高的F-Score值用粗体显示,次高的F-Score值加下划线显示.由此表可知,本文算法的F-Score指标平均值均高于4种对比算法.在从Karate到Amazon的6个数据集上,本文算法的F-Score值相比于次高的F-Score值分别提高了2.13%、3.42%、6.86%、2.12%、3.35%以及7.94%. 表1 算法在真实数据集上的F-Score指标对比结果Table 1 F-Score metrics comparison results of algorithm on real datasets 图6展示各算法在真实数据集上的运行时间.由图可知,本文算法的运行时间明显低于各对比算法.由于DBLP数据集和Amazon数据集规模较大,各算法在这两个数据集上的运行时间远大于在其它4个数据集上的运行时间.考虑到篇幅和图形的美观,设置了断层. 图6 不同算法在真实数据集上的运行时间Fig.6 Running time of different algorithms on real datasets 图7展示了各算法在人工数据集上的对比结果.图7(a)展示的是各算法Precision指标平均值的对比结果.由此图可知,本文算法和LCDFSR算法的Precision指标平均值要高于其它3个对比算法.在μ值分别为0.25、0.4和0.5时,本文算法的Precision指标平均值略低于LCDFSR算法;在μ取其它6个值的情况下,本文算法的Precision指标平均值与LCDFSR算法持平. 图7 在人工数据集上的实验结果Fig.7 Experimental results on the artificial datasets 图7(b)展示的是各算法Recall指标平均值的对比结果.由此图可知,本文算法的Recall指标平均值仅在μ值分别为0.45和0.5两种情况下略低于MULTICOM算法;在μ取其它7个值的情况下,本文算法的Recall指标平均值均高于所有对比算法. 表2展示了各算法在人工数据集上F-Score指标的平均值,最高的F-Score值用粗体显示,次高F-Score值加下划线显示.由此表可知,本文算法的F-Score指标平均值均高于4种对比算法.在4个对比算法中,LCDMD算法在值分别为0.4、0.45和0.5时相对于其他3个算法表现最好,在取其他6个值时,LCDFSR算法相对于其他3个算法表现最好.本文算法在取前6个值时的F-Score指标平均值相对于LCDFSR算法分别提高了0.77%、3.07%、6.67%、7.90%、8.71%和20.37%,在取后3个值时的F-Score指标平均值相对于LCDMD算法分别提高了21.51%、19.47%和20.70%.图8展示了各算法在人工数据集上的运行时间.由图可知,与LCDMD算法、MULTICOM算法和MLC算法相比,本文算法的运行时间更短.与LCDFSR算法相比,本文算法的运行时间则略长.但考虑到本文算法的F-Score值要明显高于LCDFSR算法,而且在值增大的过程中,LCDFSR算法的F-Score值下降剧烈,而本文算法则表现较为平稳,故认为本文算法更优. 表2 算法在人工数据集上的F-Score指标对比结果Table 2 F-Score metrics comparison results of algorithm on artificial datasets 图8 不同算法在人工数据集上的运行时间Fig.8 Running time of different algorithms on artificial datasets 本文提出了一种局部社区划分方法.该方法将局部社区划分分为种子社区构建和种子社区扩展两个阶段.在种子社区构建阶段,根据节点间的相似程度和连接紧密程度生成种子社区.在种子社区扩展阶段,引入节点的两级筛选机制,利用该机制将在相似程度和连接紧密程度两方面优势均衡的节点作为最佳的节点,合并到当前社区,以提高社区划分结果的合理性.两级筛选机制允许在一次迭代过程中合并多个节点,以提高社区扩展过程的收敛速度.在多个真实数据集和多个人工数据集上的对比实验证明了本文方法的正确性和有效性.2.4 算法复杂度分析
3 实 验
3.1 实验数据
3.2 评价指标
3.3 实验参数
3.4 真实数据集上的对比实验与分析

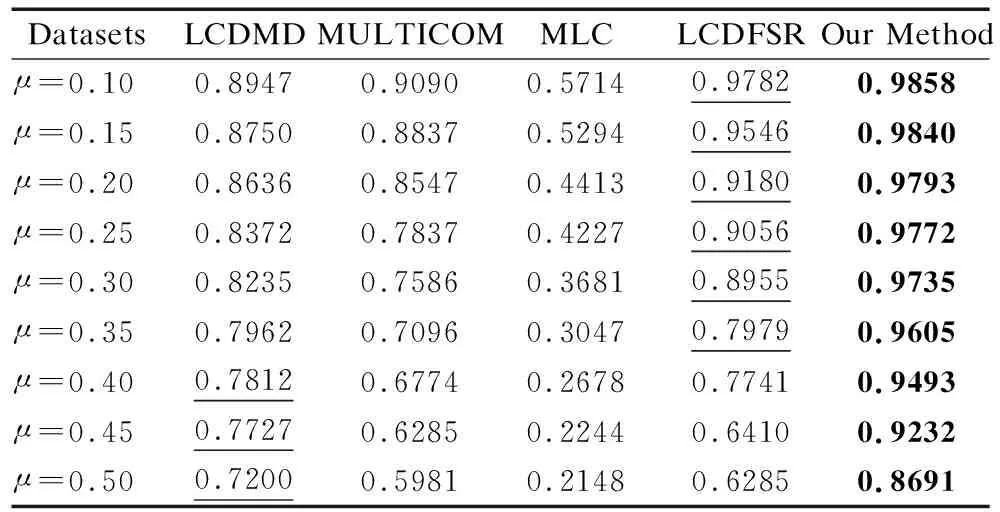
3.5 人工数据集上的对比实验与分析

4 结束语

