改进人工蜂群算法求解柔性作业车间调度问题

成金海,徐 华

(江南大学 人工智能与计算机学院,江苏 无锡 214122)

0 引 言

调度问题是制造流程规划和管理领域中一个重要问题,其中作业车间调度问题(Job-shop Scheduling Problem,JSP)是这个领域中最困难的问题之一[1].FJSP是经典JSP的拓展,FJSP存在多对多映射关系,工序可以由不同的机器加工,机器也可以加工不同的工序,是典型的非确定性多项式难(Non-deterministic Polynomial Hard,NP-hard)组合优化问题.在实际的车间优化调度问题中,多目标柔性作业车间调度(Multi-Objective Flexible Job-shop Scheduling Problem,MOFJSP)是比单目标FJSP更困难但更贴近车间实际生产环境的车间调度优化问题.

近年来,MOFJSP受到广泛关注,学术界产生了大量成果.其中,Zhang[2]等设计了两层遗传算法,使用新的交叉策略求解多目标问题,算法获得了一定数量的非支配解,拥有较好的深度搜索和跳出局部最优的能力.Dong[3]等设计了一种四食物源编码方法,结合入侵肿瘤生长优化算法结构和NSGA-Ⅲ中对解的筛选机制,提出一种收敛更快且解集分布更均匀的多目标算法.Soto C[4]等设计一种并行分支定界法求解MOFJSP,实现15.64倍的时间加速比,提高搜索Pareto解集的效率.Wu[5]等提出一种改进灰熵关联度的适应度值分配策略,设计一种基于正态云的状态转移模型,能够有效提高精度和加快收敛速度.

人工蜂群算法(Artificial Bee Colony,ABC)是一个由蜂群行为启发的算法,在2005年由Karaboga小组为优化代数问题而提出[6].在车间调度领域,Zhao[7]等人为克服单一算法在求解MOFJSP时在最优性和多样性方面产生的不足,提出一种多策略融合的人工蜂群算法,实现协同搜索,获得全局和局部最优的平衡.Zheng[8]等针对模糊FJSP设计一种基于邻域搜索的改进人工蜂群算法,采用四种邻域结构增加局部搜索能力,设计一种新颖的交叉方式加速种群的收敛,较好的解决了以最小化最大模糊完工时间为目标的模糊柔性作业车间调度问题.Li[9]等设计一种基于禁忌搜索的混合人工蜂群算法,在初始化阶段使用基于聚类分组的轮盘赌方法产生种群,有效的解决纺织行业的实际FJSP.

从现有文献可以观察到MOFJSP是当前热门的调度问题,MOFJSP涉及组合优化问题,在组合优化领域常用Pareto解集来表示一组优化解.ABC算法作为启发式算法,在组合优化问题方面有一定运用.MOFJSP为获得精度和速度的平衡,对于各单目标的搜索水平有限,且多数算法是从优化算法结构、调整参数、改进搜索策略等角度进行优化,在解决大规模问题时仍存在局限.因此本文提出一种基于分支限界法思想的数据预处理方式来排除无效的搜索空间,多数文献使用单一的进化方式并不能体现个体差异,本文根据蜂群个体的差异性使用多种进化策略,使用学习策略激发种群活力,设计两条规则避免碰撞搜索,将人工蜂群算法应用于求解FJSP,提出MCMSABC,并通过多个测例和实例验证其有效性.

1 FJSP数学模型

1.1 FJSP

FJSP涉及两个主体:一是工件集合J={Ji,1≤i≤n},二是机器集合M={Mk,1≤k≤m},每个工件由βi(βi>0)道工序组成,共有Dim道工序组成.解决该问题是在约束条件下确定工序间的加工顺序和每个工序选择的加工机器,使各指标达到最优值.

1.2 符号定义

Oi,j:Ji号工件的第j道工序;

Pi,j:Oi,j的加工机器集合;

Si,j,k:Oi,j在机器k上的加工状态,Si,j,k=1表示Oi,j能在机器k上加工,Si,j,k=0则不能加工;

Ti,j,k:Oi,j号工序在机器k上的加工时间;

Ci:Ji号工件的加工完成时间;

Dh:第h道工序在不同机器上的加工时间集合;

Prk:机器k的加工成本.

1.3 目标函数

FJSP主要关注以下几个目标:最大完工时间,机器加工最小总负荷,单个机器最大负荷,加工成本等.本文主要研究以下3个目标:

1)最小化最大完工时间:

F1=min{Ci|1≤i≤n}

(1)

2)最小化机器加工总负荷:

(2)

3)最小化单个机器最大负荷:

(3)

1.4 约束条件

1)机器不存在物理故障,工序之间无等待时间,任一工序加工过程为连续过程.不同机器在零时间开始独立工作.

2)同一工件的工序有加工顺序,后一工序须等待前一工序加工完成,即Oi,j完成后才可加工Oi,(j+1).

3)任一机器在某一时刻只能加工一个工序,即在某一时刻,存在Si,j,k=1时,必不会存在Sz,v,k=1,(z≠i,v≠j).

2 MCMSABC求解FJSP

2.1 编码和解码

本文根据FJSP特点使用分段式编码,蜜源向量由机器编码和工序编码组成,机器编码长度和工序编码长度均为各工序的工件数量总和.

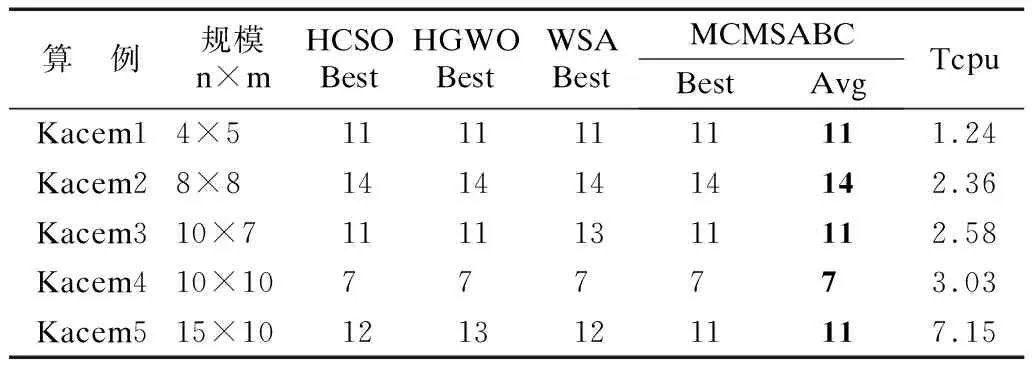
图1展示了蜜源向量的编码序列,机器序列对应的工序顺序为O1,1…O1,β1…Oi,1…Oi,βi…On,1…On,βn,每个工序的加工机器集合为{Mi,Mj…Mk,i

图1 蜜源向量编码Fig.1 Coding of honey source vector

机器编码中的数字代表该工序选择的机器在集合中的位置,如J3的第2个位置的数字“2”,则表示为J3的第2个工序选择机器库中的第2个机器,即M3;工序序列中的第1个数字“2”,表示J2的第1个工序被加工,即O2,1是第2个被加工的工序.

解码是将蜜源向量中的机器信息和工序信息转换成一个可行的调度方案,将工序插入到对应机器上最早可行的时刻加工有利于最小化最大完工时间,因此使用贪婪插入法[10]生成调度方案.

2.2 种群初始化

初始化蜂群的优劣对整个搜索过程有着关键的影响,较好的初始化策略有利于提高蜂群的求解质量.本文在初始化机器序列时,使用Zhao等[11]提出的基于机器序列的改进全局和局部选择方法,并使用逻辑混沌映射产生个体,增加种群多样性.公式(4)是逻辑映射的数学表达式,Xi,t为第i个个体第t道工序选择的机器在机器集合中的位置,μ是逻辑映射参数,当μ=4时,系统处于完全混沌状态,产生的初始蜂群分布最广,通过逻辑混沌映射产生个体的机器序列.

Xi,(t+1)=μXi,t*(1-Xi,t),Xi,t∈(0,1)

(4)

公式(5)是为满足FJSP离散的特点,将个体向量从连续空间映射到离散空间.其中NJt表示第t道工序可选的机器总数,low=1表示每个工序至少能被一台机器加工,round为四舍五入函数.

Xi,t=round(1+(NJi-1)*Xi,t)

(5)

在工序序列初始化时,使用Zhao[7]等提出的MWR、MOR和RS的排序规则.其中,MWR是优先加工剩余工作量较大的工件,MOR是优先加工剩余工序量较大的工件,RS是随机加工未完成的工件.

改善全局策略、改善局部策略、随机策略使用比例为0.4,0.4,0.2,MWR、MOR、RS使用比例为0.4,0.4,0.2,机器序列和工序序列随机组成个体序列.

2.3 改进快速非支配排序策略和精英档案

初始化蜂群后需评价个体质量.Deb等提出NSGA-Ⅱ处理多目标优化问题,使用快速非支配排序和拥挤距离评价个体的优劣和密集程度[12].本文选用F1,F2,F3作为个体指标.P、Q为两蜂群个体,若P、Q满足条件(6),则P支配Q,P质量高于Q.

(6)

根据条件(6),若P的多目标值为(14,81,12),Q的多目标值为(15,75,12),此时P与Q互不支配,但实际搜索过程中,P的多目标值由于工序序列不合理,产生(15,81,12),(16,81,12)等多目标值,此时被Q支配,从而导致潜力蜜源未被完全开发.针对此问题,本文提出改进策略,在条件(6)基础上添加条件(7).两个体F3相等时不作为支配的条件,该支配条件能够保留潜力个体,对个体进行深度开发,增大多目标搜索的空间.

F3(P)

(7)

多目标问题中蜂群探索蜜源,若探索一次蜜源,蜜源质量未变好,则该蜜源的被搜索次数增加1,反之归0.在每一轮迭代过程中,使用快速非支配排序得到每个蜂群的最优个体集合,即该蜂群的Pareto解集,称为该蜂群的精英集合.将每轮迭代过程中每个蜂群的精英集合汇入一个档案,对档案中的个体进行快速非支配排序,得到当前搜索到的最好个体集合,称为精英档案,档案中的个体称为精英个体.

2.4 蜂群进化策略

由于蜂群个体的初始化质量差异性较大,使用单一的进化策略会减慢收敛速度和降低求解质量,采用多蜂群的策略可以提高蜂群进化的有效性.本文使用性别判定法[13]将蜂群按照分割比例分为蜂王群和工蜂群,增强进化的适应性.蜂群性别判定法步骤如下:

Step1.设置蜂群数量Fnum,测试蜂群数量Tnum,蜂群分割比例γ,初始化测试蜂群.

Step2.计算个体繁殖能力,即能寻出优秀蜜源的数量.在机器序列上随机选择测试蜂中两个工序的机器替换原蜂对应工序的机器,在工序序列上测试蜂和原蜂使用常见的基于工件顺序的交叉方式(Precedence Order-based Crossover,POX)生成新工序.若生成的新个体支配原个体,则该个体繁殖能力加1;

Step3.选择繁殖能力大的前Fnum×γ个个体进入蜂王群,其余进入工蜂群;若繁殖能力相同,则优先考虑有较小F1的原蜂,其次考虑有较小F3的原蜂,若全部相同,则随机选择.

在蜂群探索蜜源的过程中,会产生多个互不支配的解,会存在是否更新原个体的问题,此时不更新原解,将另一非支配解添加至伴生蜂群.为达到快速收敛和增大搜索空间的平衡,需要对伴生蜂群进行裁剪,控制其数量,裁剪过程中使用Harmonic平均距离[14]作为评判标准,该距离与拥挤距离相比能较好的评价个体间密集程度.控制伴生蜂群数量裁剪步骤如下:

Step1.设置伴生蜂群最大数量Nmax=Fnum×p,伴生蜂群Group当前数量为Npre,伴生比例p,Group中精英个体比例为q,设置容量为Nmax的伴生数组Set,Set当前容量Ncur,转Step 2;

Step2.若Npre不大于Nmax,则将Group中个体全部加入Set,转Step 7,否则转Step 3;

Step3.使用改进的快速非支配排序计算伴生蜂群中Pareto解集中解的数量N1,若N1≤Nmax×q,则全部加入Set,更新Ncur,转Step 5,否则转Step 4;

Step4.计算Pareto解集中个体的Harmonic平均距离,删除平均距离最小的个体后,若解集中剩余个体数量等于Nmax×q,则全部加入Set,更新Ncur,转Step 5,否则转Step 4;

Step5.使用改进的快速非支配排序计算Group中剩余个体的Pareto解数量Npf,若加入Set后Ncur大于Nmax,则计算解集中个体Harmonic平均距离,删除平均距离较小的若干个体,使剩余个体加入Set后使Ncur等于Nmax,转Step 7,否则转Step 6;

Step6.将该层Pareto解集全部加入Set,若无剩余个体,转Step 7,否则转Step 5;

Step7.将Set更新为Group,算法结束.

该算法伪代码如下:

算法.更新伴生蜂群

输入：蜜蜂数量Fnum,裁剪比例p,精英比例q,大小为Npre伴生蜂群Group

输出：伴生蜂群Group

1.创建大小为Nmax=Fnum×p的伴生数组Set,记容量为Ncur

2.if(Npre>Nmax)then

3. 计算Group中精英个体数量为N1

4. while(N1>Nmax×q)do

5. 计算Harmonic平均距离,删除距离最小个体

6. end while

7. 将剩余精英个体加入Set,更新Ncur,更新Group

8. While(Ncur0)do

9. 计算Group的Pareto解集中个体数量Npf

10. if(Npf+Ncur≤Nmax)then

11. 将Npf个个体加入Set,更新Group

12. else

13. 计算Npf个个体平均距离删除若干距离最小的个体后加入Set

14. end if

15. end while

16.end if

17.将Set更新为Group

18.return Group

2.5 雇佣蜂阶段

标准ABC多用于解决连续型函数问题,在雇佣蜂阶段对个体给定一个随机方向和微小的步长进行邻域搜索.FJSP属于离散问题,标准ABC邻域搜索会产生无效解,因此本文根据繁殖能力使用多种有效邻域结构,将搜索中产生的非支配个体加入伴生蜂群.

机器邻域结构:

1)随机选取1至2个工序的加工机器变异,选取产生最好解的一组变异方式更新.若选择的工序个数为1,则在该工序的机器集合中选择一个使个体最优秀的机器,若选择的工序个数为2,则如图2(a),从第1道工序和第6道工序的机器组合方案中选择使个体最优秀的一组方案,即机器M1和M3.

图2Fig.2

2)确定最大负荷机器,将该机器的一道加工工序指派到另一机器加工.

3)确定加工工序数量最多的机器,将该机器的一道加工工序指派到另一机器加工.

4)随机选择若干工序,选择该工序加工时间最小的机器.

工序邻域结构:

1)随机选择两道工序,将前一道工序插入到后一道工序后或将后一道工序插入到前一道工序前,若选择的工序属于相同工件,则重新选择.

2)随机选择两道工序交换,若选择的工序属于相同工件,则重新选择.

3)计算每个工件工序的位置下标之和,选取最大和最小两个工件,打乱两个工件的工序次序,并放回原序列中工序所在位置.如图2(b)中,J1的加工顺序位次和为7,J2的加工顺序位次和为5,J3的加工顺序位次和为9,则将J2和J3的工序打乱顺序后填入原位置.

工蜂群使用机器结构比例为0.3,0.3,0.3,0.1,工序结构的比例为0.4,0.4,0.2.蜂王群使用机器结构比例为0.1,0.2,0.2,0.5,工序结构比例为0.25,0.25,0.5,伴生蜂群结构使用比例和蜂王群相同.

2.6 观察蜂阶段

在标准ABC中雇佣蜂阶段蜂群对蜜源进行邻域探索后,观察蜂阶段蜂群根据适应度值选择蜜源,适应度值大的蜜源被选择概率大.在多目标问题,标准ABC选择蜜源的方式已不适合,需要改变评价蜜源适应度评判指标,对于不同蜂群提出两种竞争方式.工蜂群繁殖能力弱,个体差异小,使用轮盘赌方法选择蜜源具有公平性,概率选择如公式(8),Bj为第j个个体支配其余个体的数量,B为所有个体支配其余个体数量的总和,Proj是个体被选择的概率.

(8)

蜂王群繁殖能力强,个体差异大,因此使用一种基于损失值的排序方式选择蜜源,通过比较损失值体现个体的差异性,为防止个体差异性太大导致个别蜜源被选择概率极低,根据损失值将蜜源进行排名.损失值计算如公式(9),Fi表示该个体的第i个目标值,Fimin为第i个目标搜索到的最小值.

(9)

使用公式(10)计算蜜源选择概率,其中index(j)表示第j个个体在蜂群中的排名,num是蜂王群数量,Iter是最大迭代次数.当解的Loss最小时,index(j)=1.在算法初期,I较小时,φ较小,可避免蜂群搜索陷入局部最优,保持蜂群多样性;在算法后期,个体差异小时增大φ值提高较差个体被选择的概率加速种群探索,防止算法搜索陷入停滞状态.

(10)

不同蜂群在观察蜜源时使用的策略不同,在观察蜜源时产生的非支配个体加入伴生蜂群.蜂王群对于工序序列使用POX交叉,机器序列使用常见的均匀交叉(Uniform Crossover,UX);工蜂群对于工序序列使用基于工件的交叉方式(Job-based Crossover,JBX),机器序列使用多点交叉(Multiple Point Crossover,MPX).

JBX交叉规则:选择父代序列P1和P2,将工件集合JS随机分为JS1和JS2,将P1中属于JS1,P2中属于JS2的工序分别复制到产生到子代序列O1和O2中相同位置,再将P1中属于JS1,P2中属于JS2的工序按照原顺序分别复制到O2和O1的空位置.

MPX交叉规则:选择父代序列P1和P2,产生一个与工序数量相同的“0-1”向量,若该向量某位置为0,则将P1中机器复制M1,P2中机器复制到M2,若为1,则将P1中机器复制M2,P2中机器复制到M1.

在标准ABC中邻域搜索在雇佣蜂阶段,本文在观察蜂阶段使用基于关键路径的邻域搜索策略,提高进化精确性.由于一个调度方案具有多条关键路径,导致关键路径内的关键块所含的关键工序的数量也不同,因此对于包含不同数量关键工序的关键块需要设计不同的邻域结构.N6[15]和M&G[16]两种邻域结构能够保证连通性并缩小邻域规模,在FJSP上得到了广泛的应用.基于连通性要求和小规模邻域结构能获得精度和速度的平衡.根据此邻域结构设计思想,本文提出3种基于关键路径的邻域结构MaxI,MinE,RandD,要求每个关键块内的关键工序数量不少于二道,每个个体仅使用一种邻域结构.

MaxI:选择包含最多道关键工序的关键块,将关键块内的一道工序插入到块首工序前或块尾工序后,该关键块内关键工序数量不少于3道.

MinE:选择包含最少道关键工序的关键块,将关键块内的一道工序与相邻工序进行交换,该关键块内工序数量不超过3道.

RandD:将关键块内加工时间最长的一道工序指派到其他机器,若该工序仅有一个可加工机器,则尝试次长工序的机器指派.

上述3种基于关键路径的邻域结构需要满足以下两条规则,否则为无效邻域.

1)关键块内某工序向前插入或交换时,其开始加工时间必须大于前序工序结束时间.

2)关键块内某工序向后插入或交换时,其结束加工时间必须小于后续工序开始时间.

基于关键路径的邻域结构如图3所示,(i,j)表示Oi,j,在满足两条规则时,当(1,1)和(2,1)是关键块时,则可以使用MinE邻域结构;当(4,2),(2,2),(1,3),(2,3)是关键块时,则可以使用MaxI邻域结构,当(2,4),(3,3)是关键块时,则可以使用RandD将(3,3)的机器变更为M1.

图3 基于关键路径的3种邻域结构Fig.3 Three neighborhood structures based on critical path

2.7 侦察蜂阶段

在经历雇佣蜂和观察蜂阶段之后,需要对无潜力的个体进行更新,以此保证种群的活力,在标准ABC中,侦察蜂会放弃探索次数超过Limit的蜜源,重新探索新蜜源.由于探索过程的随机性,无法保证新蜜源质量.本文在侦察蜂阶段加入基于学习机制的策略更新蜜源,学习优秀个体能够加快蜂群收敛,提高新蜜源质量.基于学习机制的更新策略如下:

1)在机器部分将精英个体加入蜂群,对蜂群使用混合列交叉[17],在工序部分选取精英个体,与蜂群个体使用JBX交叉方式;

2)对于1)中的个体,若该个体连续探索蜜源次数超过仍Limit未发现质量高的蜜源,则

(1)使用随机初始化策略重构个体;

(2)使用学习策略将个体重构,使用学习策略重构个体步骤如下:

Step1.从精英档案中随机选取一个精英个体,随机选取精英个体机器编码段的两个位置.若两位置距离小于Dim/2,转Step 2,否则转Step 3;

Step2.将精英个体两个位置之间的编码段复制给子代个体,将原个体中剩余两侧的编码段复制给子代个体.工序序列选定同样位置,将原个体两个位置之间的编码段复制给子代个体,剩余两侧的编码段打乱后复制给子代个体,转Step 4;

Step3.将原个体两个位置之间的编码段复制给子代个体,将精英个体中剩余两侧的编码段复制给子代个体.工序序列选定同样位置,将原个体两个位置之间的编码段打乱后复制给子代个体,剩余两侧的编码段复制给子代个体,转Step 4;

Step4.算法结束.

2.8 算法流程

算法分为5个阶段,阶段如下:

Step1.初始化阶段:输入工件和机器信息,使用2.4节的策略产生蜂群,计算个体适应度,使用快速非支配排序更新精英档案.设置蜂群个数等基础参数、性别判定法相关参数、邻域结构相关参数,转Step 2.

Step2.雇佣蜂阶段:使用性别判定法将蜂群拆分为蜂王群和工蜂群,蜂王群和工蜂群根据产生的随机数与参数的大小关系选择2.5节中提出的对应邻域结构.若蜂王邻域结构的使用阈值为a,a+b,a+b+c,1,则产生一个随机数y,若a

Step3.观察蜂阶段:蜂王群和工蜂群使用2.6节的两种竞争方法选择个体,选择2.6节的蜂群对应交叉方式进行交叉.对所有个体使用基于关键路径的邻域探索策略,产生精英集合,更新档案.伴生蜂群使用蜂王群交叉算子和基于关键路径的邻域探索后使用裁剪策略,产生精英集合,更新档案,转Step 4.

Step4.侦察蜂阶段:对于蜂王群和工蜂群使用2.7节1)策略进行个体更新,使用2.7节2)策略进行个体重构,并将蜂王群和工蜂群合并,伴生蜂群作为独立蜂群.若迭代结束,转Step 5,否则转Step 2.

Step5.结束阶段:输出更新后的精英档案.

2.9 针对单目标改进的算例数据预处理策略

对于任一工序都能被所有机器加工的FJSP称为完全柔性作业车间调度问题(Total Flexible Job-shop Scheduling Problem,T-FJSP),由于T-FJSP存在较大的无效搜索空间,因此对算例进行数据预处理.分支限界法是找出满足约束条件的解,设计合理的剪枝函数能够在早期淘汰不良个体,FJSP是优化问题,剪枝函数设计应参考目前搜索的最小值,在算例中排除加工时间过长的情况.记测试蜂群的F1min为SC,对于Ti,j,k提出两条规则:

规则1.由于F1≥F3,若Ti,j,k>SC,则从此工序的Pi,j中删除该机器;

规则2.删除Ti,j,k较大的加工机器,满足约束条件(11)时从此工序的Pi,j中删除该机器,ceil是向上取整函数,rand产生0到1的随机数,τ是规则2的系数,m是机器数量;

(11)

2.10 针对多目标改进的蜜源更新策略

由于蜜源的潜力有限,且蜜源质量取决于机器向量和工序向量两部分,机器向量决定蜜源质量上限,当蜜源质量达到上限时,改变工序序列不会改进解的质量,会产生无效的碰撞搜索.因此设计两种方案提高蜜源质量上限.从精英档案中随机选取一个精英,其探索的蜜源目标值分别为F1,F2,F3,蜂群中一个体探索的蜜源目标值为FC1,FC2,FC3,当满足条件(12)或(13)时,需要重构机器序列.满足条件(12)时,该个体解被精英解支配,不会在全局上产生更优解;满足条件(13)时,该个体解已达最优.

FC2≥FJ2,FC3≥FJ1

(12)

FC3=FC1

(13)

3 实验与结果分析

为验证MCMSABC有效性,本文从Kacem等[18]提出的5个算例和Brandimarte[19]等提出的5个算例验证算法,并通过车间实例验证算法的实用性.Tcpu为10次实验中算例运行的平均时间(单位:min).

算法由matlab2021a编写,运行环境为:8GB,CPU为i5-6300.针对不同算例运行10次,并与文献比较.参数:Fnum=80,Iter=300,Limit=30,γ=0.5.

3.1 单目标FJSP实验分析

表1显示了MCMSABC与HCSO[20]、HGWO[21]、WSA[22]在F1上的结果,其中Best为10次实验的最优解,Avg为10次实验的平均解,I(O)为10次实验中达到O值的平均迭代次数,若未能搜索到O值则为最大迭代次数.对于Kacem1、Kacem2和Kacem4 3个算例,MCMSABC搜索到的Avg和Best均为最优值;对于Kacem3,WSA搜索到的Best是13,MCMSABC搜索到的Best是11,将Best减小2;对于Kacem5,HCSO和WSA搜索到的Best是12,HGWO搜索到的Best是13,MCMSABC能搜索到其余3种算法未搜索到的Best值11,且Avg为11,说明MCMSABC求解质量优于对比算法.

表1 F1单目标Kacem算例对比结果Table 1 Comparison results of single target(Kacem examples)

为了验证规则1和规则2的合理性,在不使用初始化和伴生蜂群策略的条件下对MCMSABC、MCMSABC1(应用规则1)、不同参数下的MCMSABC2(应用规则2)进行实验.表2显示了4个T-FJSP在不同规则下的Avg和I(O).MCMSABC1比MCMSABC具有较小的I(O)和Avg,说明较小的搜索空间能加速搜索到最优解,体现了规则1的合理性.τ较小时,MCMSABC2比MCMSABC有较小的I(O)和Avg,体现了规则2在解决T-FJSP时具有一定的合理性.

表2 不同规则下的最优解和迭代次数Table 2 Optimal solution and iteration times under different rules

表3显示了MCMSABC在MK算例上的F1和文献[2]、HCSO[20]、HGWO[21]、IDSSA[23]、文献[24]、文献[25]的比较结果,加黑值为比较算法搜索到的最优解.对于MK01、MK03,MCMSABC和其余算法均能搜索到Best,且Best和Avg相等;对于MK05,MCMSABC和文献[24]算法能够搜索到Best172,相对于其余算法搜索到的Best更优;对于MK07,MCMSABC和文献[25]算法均能搜索到Best139,相对于HCSO、HGWO、WSA、IDSSA将Best值缩小5以上;对于MK09,MCMSABC相对于HCSO、HGWO、文献[24]算法、IDSSA均能将Best值更新,相对于WSA将Best缩小62.MCMSABC在5个算例上的Avg与Best均不超过1,说明MCMSABC性能优于对比算法,求解大规模算例时具有稳定性.

表3 F1单目标Brandimarte算例对比结果Table 3 Comparison results of single target(Brandimarte examples)

3.2 MOFSJP实验分析

针对Kacem1～Kacem5这5个算例进行多目标分析,选取F1,F2,F3函数作为多目标优化函数.表4显示了MCMSABC所求Pareto解集与HTABC[26]、SAMO-Jaya[27]、CSTA[5]、RLNSGA-II[28]Pareto解集的对比结果.对于Kacem1,MCMSABC搜索到的解集能支配HTABC、CSTA解集;对于Kacem2,MCMSABC相对于HTABC能搜索到非支配解(16,73,13),(16,77,11)相对于SAMO-Jaya搜索到非支配解(15,75,12),(16,73,13),(14,77,12),相对于RLNSGA-II搜索到非支配解(16,77,11);对于Kacem3,MCMSABC解集支配HTABC、CSTA解集,并将F2最小值从61变成60;对于Kacem4,MCMSABC均能搜索到每个目标的最小值,解集中解的数量达到4个,解集支配HTABC解集,相对于SAMO-Jaya搜索到非支配解(8,42,5);对于Kacem5,MCMSABC搜索到的解集支配HTABC、CSTA、RLNSGA-II解集,相对于SAMO-Jaya搜索到非支配解(11,93,10),找到的(11,91,11)支配SAMO-Jaya的(11,93,11).这说明MCMSABC求出的Pareto解集质量较好,求解大规模多目标问题具有稳定性.观察到Tcpu时间均较小,说明算法的的时间复杂度较低,在精度和速度上获得了平衡.

表4 多目标Kacem算例对比结果Table 4 Comparison results of multi-objective(Kacem examples)

3.3 车间实例实验分析

为验证本算法在车间实例上的有效性,选取文献[29]的车间实例来测试.该车间实例的数据规模为6×6,即6个工件和6个机器.表5为实例的实验结果对比,表5中给出了MCMSABC和PDABC[17]、CEMOFJSP[29]、CSTA[5]这3种算法的比较结果.本文算法搜索到的6个Pareto前沿解均能支配3种算法的解集,对于CEMOFJSP和PDABC两种算法,在F1上得到了提升,将最大加工时间从10减少到了9.MCMSABC搜索到的F1,F2,F3均为3种算法的最优值,搜索到的Pareto解集中有6个解,解的数量最多.MCMSABC求解车间实例更加有效.

表5 多目标车间实例对比结果Table 5 Comparison results of multi-objective workshop examples

为探究本文算法在不同多目标指标下的适用性,选取文献[17]的车间算例来测试,该车间实例的数据规模为5×8,即5个工件和8个机器.使用F1,F2,F4作为多目标优化函数,其中公式(14)代表最小化机器加工成本F4,为提高种群的适应性,增加随机初始化策略的比例.本实例中随机初始化策略比例为0.4,其余策略比例为均为0.3.

(14)

表6给出了该车间实例两组多目标的Pareto解集,F1,F2均能探索到最小值,表明在修改目标函数的情况下,MCMSABC对车间实例仍具有较好的适应性.

表6 不同多目标下的解集对比Table 6 Comparison of solution sets under different multi-objective conditions

4 结 论

本文针对FJSP的特点提出一种基于多策略的多蜂群人工蜂群算法,在单目标问题上验证了数据预处理的效果,在参数适合的情况下能够获得更快的收敛速度和最优解的次数.在多目标问题上使用基于关键块大小的邻域结构,学习策略和蜜源更新策略,在算例上获得更为优秀的Pareto解集.

本文提出的算法在FJSP具有一定的实用性,通过工厂实例验证了该算法的可行性.下一步工作是研究带有约束条件的MOFJSP,满足特定环境下的车间调度问题,设计更高效的蜂群算法.